一类具有非局部项的抛物方程在Sobolev 空间的能控性
2019-11-23曾曦莫玉玲邓紫娟刘洁周秀香
曾曦,莫玉玲,邓紫娟,刘洁,周秀香
(岭南师范学院数学与统计学院, 广东湛江524048)
1 引言
给定T>0.设Q=(0,1)×(0,T).考虑如下一类具有非局部项的抛物型偏微分方程

这里a∈R(a0),y是状态函数, 给定函数b∈L2(0,1), 控制函数u∈L2(0,T), 并且y0∈L2(0,1) 是初始条件.从而, 方程(1.1) 存在唯一的解y∈L2(Q).系统(1.1) 主要用来描述一类含有关于时间的非局部反应项的扩散现象[1,2], 在物理、生物、天文、信息等领域有着广泛的应用.
当a=0 时, 系统(1.1) 是经典抛物型偏微分方程, 它是近似能控且零能控, 这是一个熟知的结果.因此, 本文主要讨论的问题是系统(1.1) 的近似能控性和零能控性.首先, 给出相关定义.
定义1.1对于任意y0,y1∈L2(0,1) 和ε>0, 存在控制u∈L2(0,T) 使得(1.1) 相应的解y满足则称系统(1.1) 在T时刻近似能控.
定义1.2对于任意y0L2(0,1), 存在控制u∈L2(0,T) 使得系统(1.1) 相应的解y满足y(x,T)=0 a.e.x∈(0,1), 则称系统(1.1) 在T时刻零能控.
关于这类系统的能控性问题已有一些相关的讨论[3−6].2000 年, Barbu 和Innelli[7]得到了如下具有二阶导数记忆项的系统的内部近似能控性

为了应用Laplace 变换给出对偶系统解的表达式, 需要假设记忆核a满足一定的条件.在文献[8]中, 作者给出了记忆核a≡1 时, 受控系统(1.2) 在L2(0,1) 空间中不零能控.随后,Halanay 和Pandolfi[9]将近似能控性和不零能控两个结果推广到一般记忆核的情况.以上讨论的结果都是建立在内部控制或者边界控制的基础上.2018 年, 文献[10]讨论了在施加双线性控制下系统的零能控性, 利用对偶理论、泰勒展式和反证法得出当系统施加双线性控制时, 系统(1.1) 在L2(0,1) 空间中不零能控.即存在初使条件y0∈L2(0,1) 使得对于任意控制u∈L2(0,T), 系统(1.1) 相应的解y在时刻T都不能达到目标零.那么一个自然的问题是,这样的结论在相对较小的Hm空间中是否成立呢? 本文给出了明确的答案.另一方面, 利用对偶原理给出在施加双线性控制下的近似能控性的充分必要条件, 它恰好是不零能控性的充分条件.
全文分为四部分, 第二部分给出控制系统关于近似能控性和零能控性的两个主要结果;第三部分主要应用对偶原理将近似能控性转化为相应对偶系统的唯一延拓性, 并得到相关结果;第四部分利用泰勒展式和反证法证明控制系统不零能控.
2 主要结果
为了给出主要结果, 先引入一些记号.设
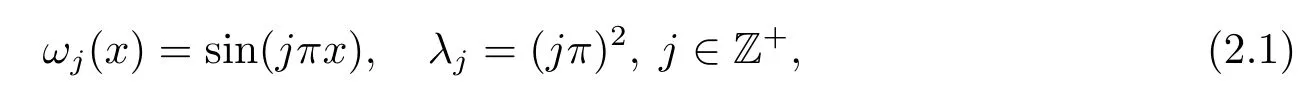
则{ωj}j≥1构成空间L2(0,1) 中的一组正交基.系统(1.1) 的对偶系统如下
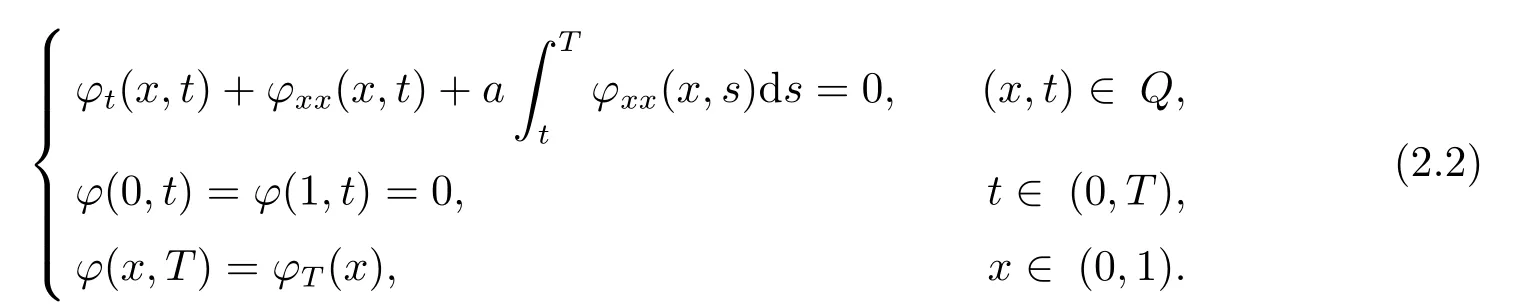
引理2.1设则对偶系统(2.2) 的解可以表示为

其中

证由于ϕT∈L2(0,1), 因此存在{βj}j≥1∈l2使得又由于系统(2.2) 的解ϕ∈L2(0,T;L2(0,1)), 因此可以表示为
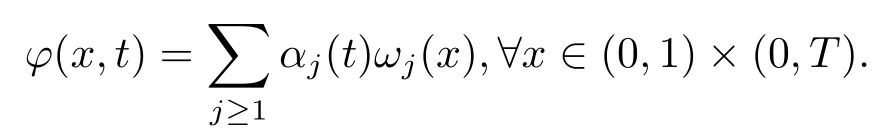
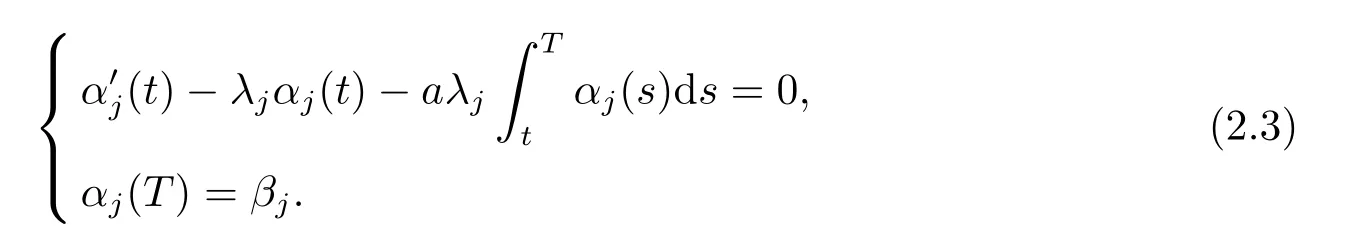

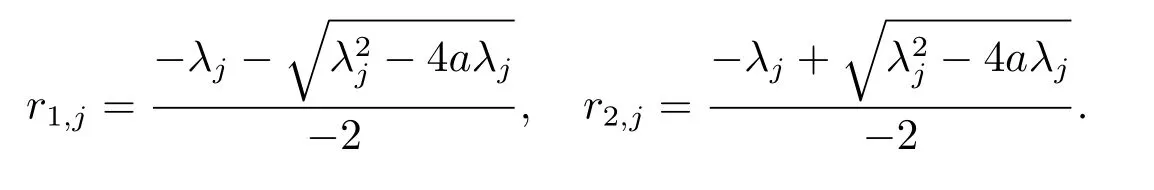

解线性方程组得
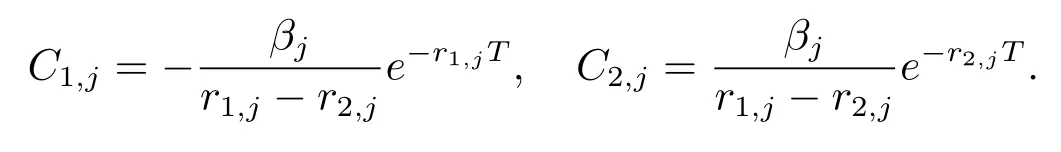
因此

令

于是方程(2.2) 的解可以表示为

引理2.1 得证.
对于任意给定m∈N, 定义Sobolev 空间

显然H0(0,1)=L2(0,1), 并且Hm2(0,1)⊂Hm1(0,1),∀m1≤m2.全文设C为只与T有关的常数.主要结果是下面的两个定理.
定理2.1下面三种陈述等价
(i) 系统(1.1) 在T时刻近似能控;
(ii) 设ϕ是对偶系统对应于ϕT的解, 则
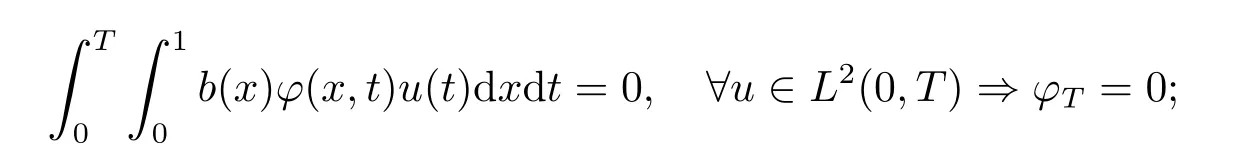
定理2.2任意给定m∈N, 设则存在初值y0∈Hm(0,1) 使得对于任意u∈L2(0,T), 系统(1.1) 相应的解都不满足

注定理2.2 中的条件不能去掉, 因为它与近似能控性等价.
3 定理2.1 的证明
证 第一步证明(i) 与(ii) 等价.
充分性要证明的结论是系统(1.1) 的近似能控性.不失一般性, 假设y0(x)≡0.由文献[10]可得

设能达集R(T)={y(·,T) |y是系统(1.1)中对应于u∈L2(0,T)的解}.由定义可知, 系统(1.1) 在T时刻近似能控当且仅当R(T) 在L2(0,1) 中稠密.采用反证法, 假设系统(1.1)在T时刻不近似能控, 则R(T) 不在空间L2(0,1) 中稠密, 由Hahn-Banach 定理得, 存在使下式成立
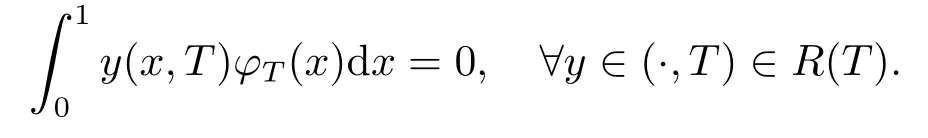
由(3.1) 式可得

因此ϕT=0, 这与假设ϕT的选取产生矛盾, 故假设不成立, 充分性得证.
必要性设

由(3.1) 式可得

第二步证明(ii) 与(iii) 等价.
充分性假设
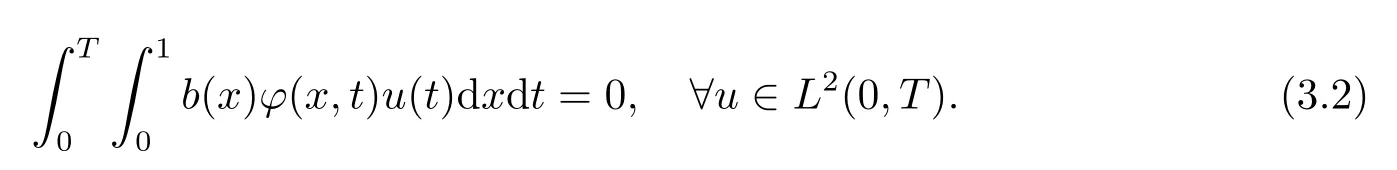
由(ii) 可知, 只需要证明βj=0,∀j≥1 即可.将(2.4) 式代入(3.2) 式得
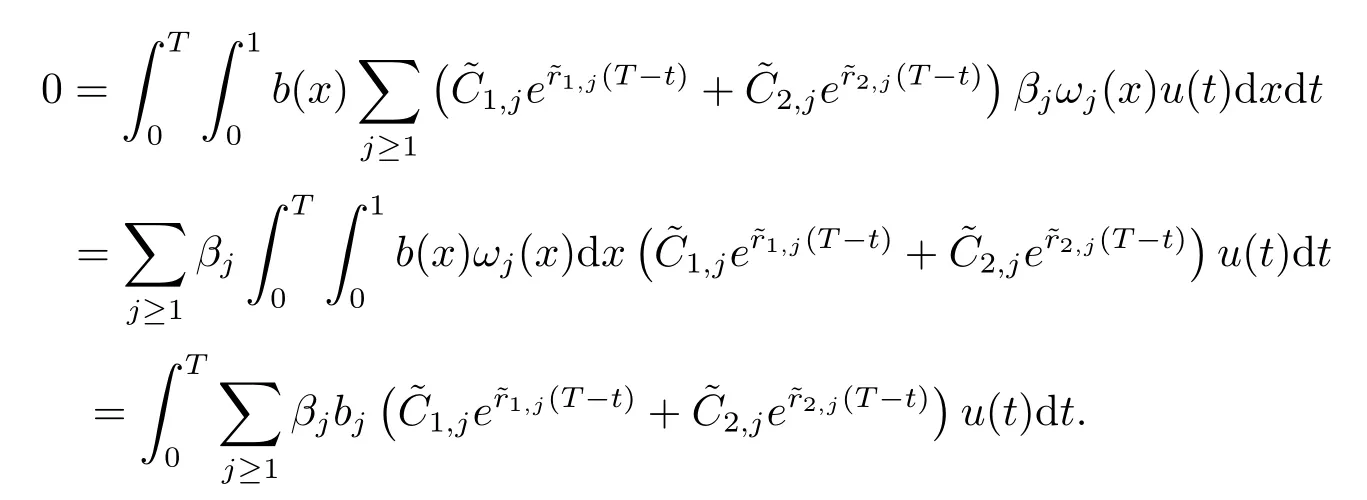
从而

必要性假设存在j0∈N, 使得bj0=0, 则利用充分性的证明过程得不到βj0一定为0,故这与条件矛盾, 所以必要性得证.故(ii) 与(iii) 等价, 综上定理2.1 得证.
注这一结论与经典抛物方程(a=0) 相同.
4 定理2.2 的证明
证 第一步构造对偶系统(2.2) 终端时刻的是一个充分大的正整数值.任意给定正整数m, 设是一个正整数.令正整数是一个充分大的正整数, 且
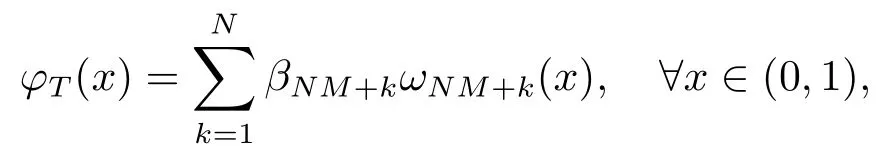
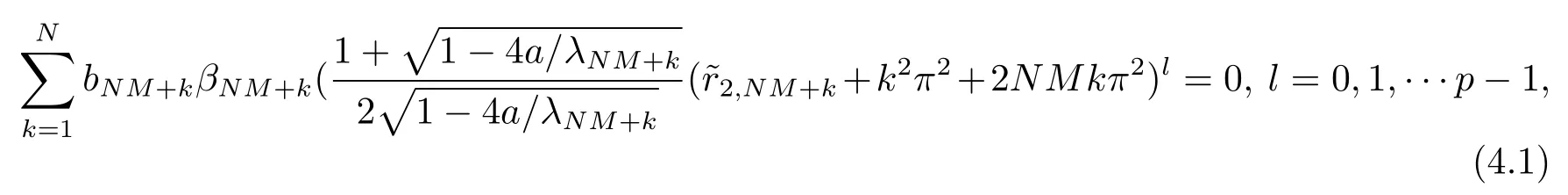
并且

联立(4.1) 和(4.2) 式是关于N个未知数个方程的代数方程组, 所以存在界与M无关的解进一步, 由引理2.1 得, 方程(2.2) 的解为

其中
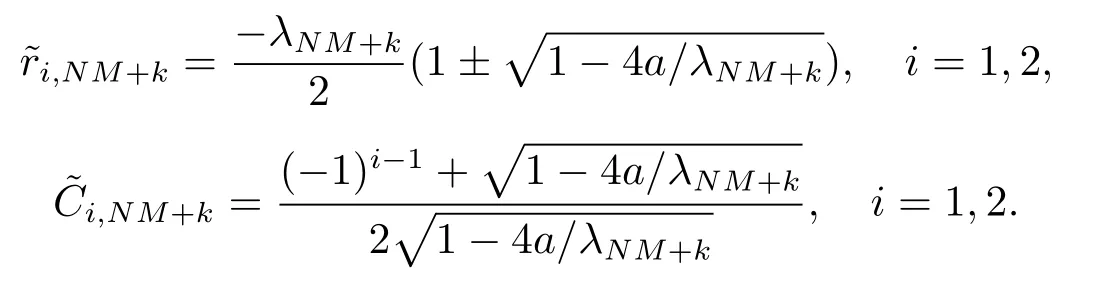
第二步给出系统(1.1) 零能控的充要条件.由文献[10]可得, 系统(1.1) 在时刻T零能控的充要条件是, 对于任意y0∈L2(0,1) 存在控制u∈L2(0,T), 使得下述的等式成立
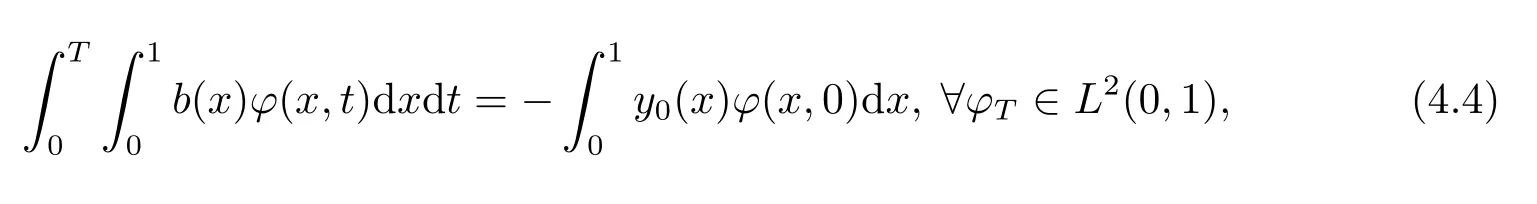
其中ϕ是对偶系统(2.2) 对应于ϕT的解.
第三步估计(4.4) 式的左端.由(4.3) 式可得

记上式最后两项分别为2E1,2E2.注意到从而
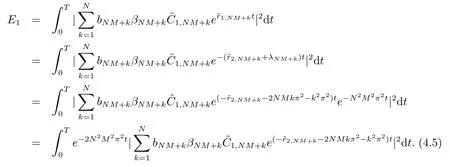
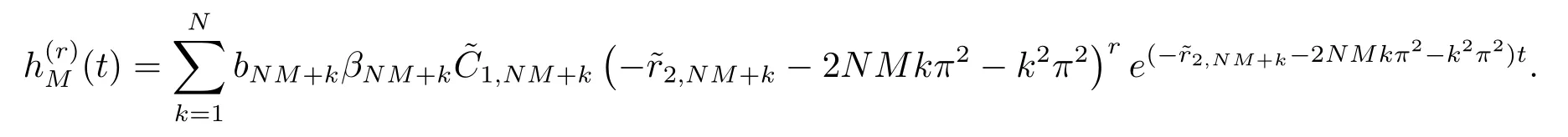
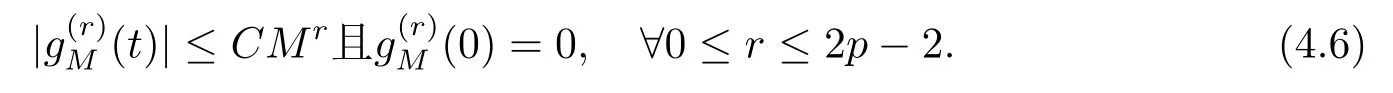
从而结合(4.5) 式和(4.6) 式并分部积分可得
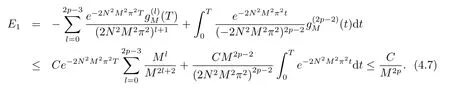
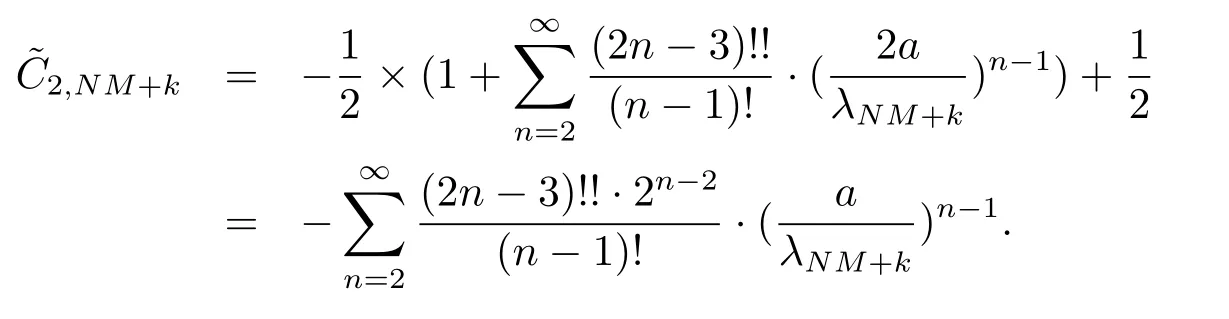
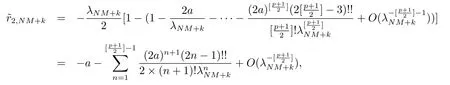
于是存在一列关于t的函数使得
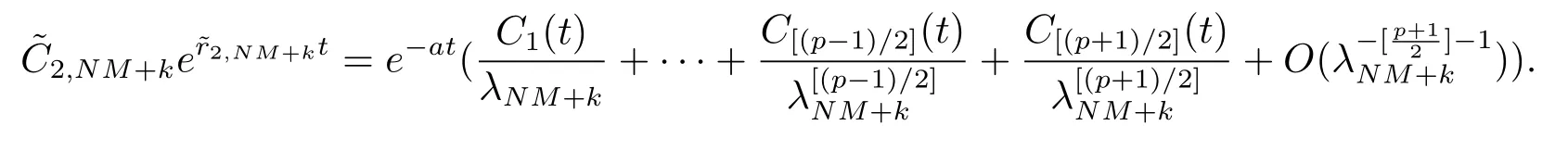
由上式及(4.2) 式可得

由(4.7) 和(4.8) 式可得
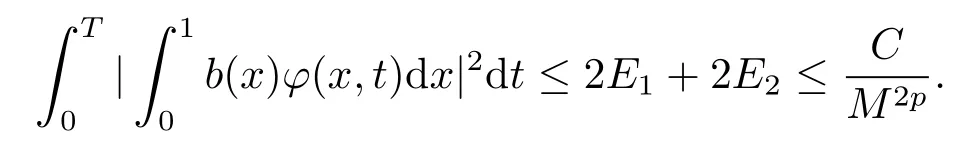
第四步估计(4.4) 式的右端.注意到

进而由(4.4) 式可得

故存在1≤k0≤N使得
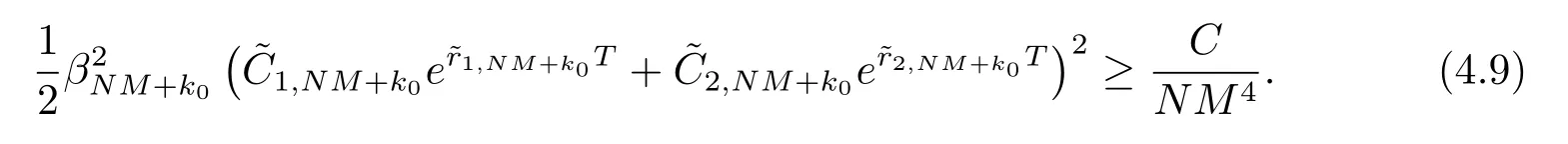
第五步构造适当初值得到结论, 即定理2.2.取则2δ−2m>1.于是
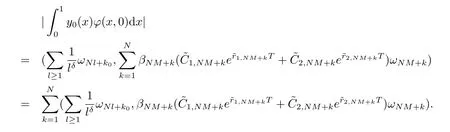
设Nl+k0=NM+k, 即N(l−M)=k−k0.由|k−k0| 假设(1.1) 在时刻T零能控, 则由证明的第二步可得, 存在u∈L2(0,T) 使得 也就是说, 存在于M无关的两个常数C1,C2使得 只要2+δ