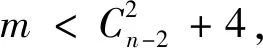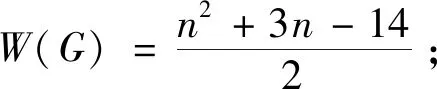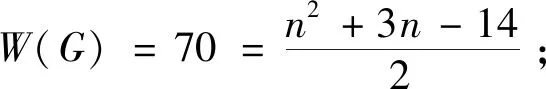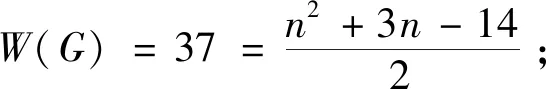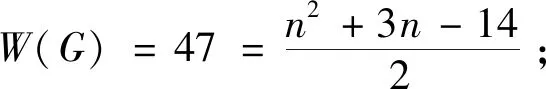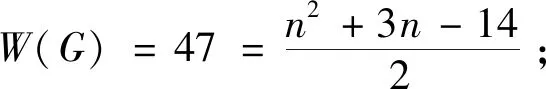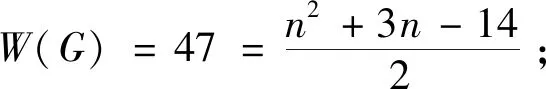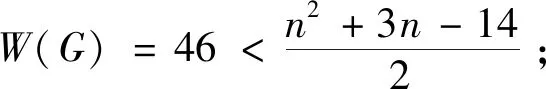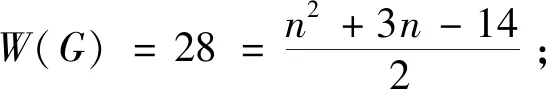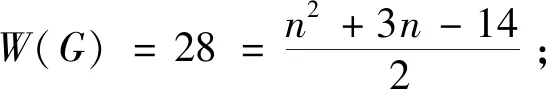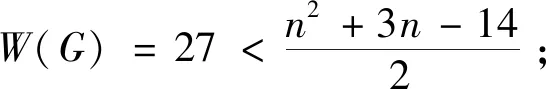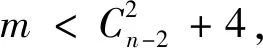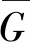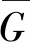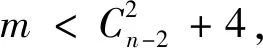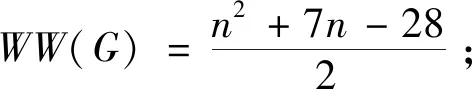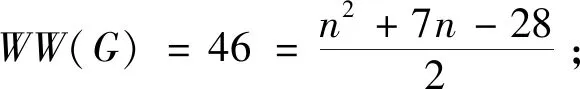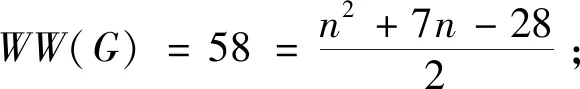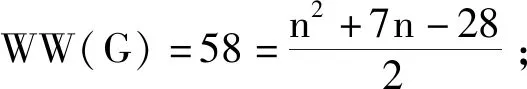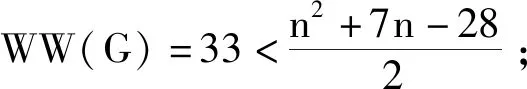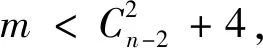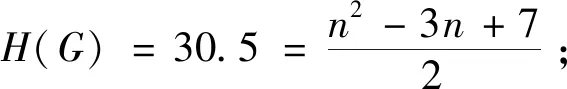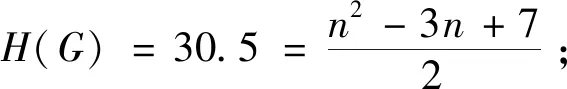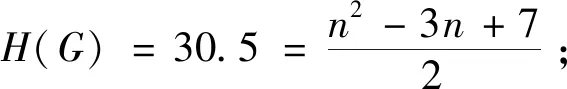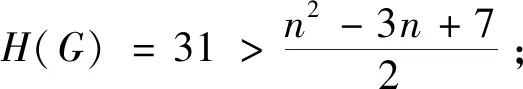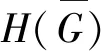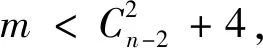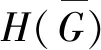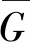利用Wiener指数、hyper-Wiener指数及Harary指数给出泛圈图的充分条件
2019-11-22胡启明
胡启明, 许 欢, 叶 铭
(合肥幼儿师范高等专科学校 公共教学部,安徽 合肥 230013)
引 言
设G(V,E)是n阶简单连通图,顶点用vi(1in)表示,顶点集{v1,v2,…,vn}用V(G)(或V)表示;边集用E(G)(或E)表示,其元素可简记作vivj(1i,jn),称为边[1]。称顶点vi(或vj)与边vivj是关联的,称边vivj的两个端点vi和vj是相邻的。若图G中的任意一个顶点vi(1in)与其他顶点都相邻,则称G为完全图,记作Kn。用或(G)c)表示图G的补图,其中是由G中所有不相邻的两个顶点连成的边组成的集合。图G中与vi关联的边数称为顶点vi的度,用dG(vi)表示,图G的最小度记为δ(G)。图G中顶点vi和vj之间所有路的最小长度称为vi与vj之间的距离,记作dG(vi,vj)。
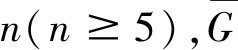
若对于任意的正整数k(3k 用G1∪G2表示G1和G2的并图,其中V(G1∪G2)=V(G1)∪V(G2),E(G1∪G2)=E(G1)∪E(G2);如果G1和G2没有公共顶点,G1和G2的并图记为G1+G2;若G1=G2=…=Gk,则G1∪G2∪…∪Gk记为kG1。 用G1∨G2表示G1和G2的联图,其等于((G1)c∪(G2)c)c,即V(G1∨G2)=V(G1)∪V(G2),E(G1∨G2)为G1的边、G2的边和由G1中每个顶点与G2中每个顶点连成的边组成的集合。 图G的Wiener指数[2]记作W(G),是指G中任意两个顶点vi和vj的距离之和,即 图G的hyper-Wiener指数[3-4]是Wiener指数的推广,记作WW(G),定义为 图G的Harary指数[5]记作H(G),是指G中任意两个顶点vi和vj的距离倒数之和,即 对于任意给定的无向图G,怎样判断它是否包含一个哈密尔顿圈?这就是举世闻名的NP完全问题。因为图的拓扑指数能很好的反映图的结构性质且便于计算,近年来人们试图利用图的拓扑指数来刻画图的哈密尔顿性,如2013年华洪波等人[6]首次用Harary指数给出了连通图有哈密尔顿路的一个充分条件。随后曾婷[7]利用Harary指数给出平衡二部图有哈密尔顿圈的一个充分条件。杨立辉[8]给出了连通图存在哈密尔顿路的关于Wiener指数的一个充分条件。Rao Li[9,10]分别给出了连通图是哈密尔顿图和哈密尔顿连通图的关于Harary指数和Wiener指数的充分条件。刘瑞芳[11,12]延伸了[7,8]中的结果。华洪波等人[13]给出了给定最小度的连通图、平衡二部图可迹性与哈密尔顿性的关于Harary指数和Wiener指数的充分条件。基于前面的研究基础,冯立华等人在[14]中又给出了k-哈密尔顿,k-路覆盖,k-边哈密尔顿的关于Harary指数和Wiener指数的充分条件。特别是最近舒阿秀等[15]研究了泛圈图的拓扑指数条件,利用图及其补图的Wiener指数、hyper-Wiener指数,给出了具有最小度条件的简单连通图是泛圈图的充分条件;余桂东等[16]给出了泛圈图的新的边数条件,以及谱半径和无符号Laplacian谱半径条件。受文献[15,16]的启发,本文利用文献[16]中泛圈图的新的边数条件,利用图及其补图的Wiener指数、hyper-Wiener指数,Harary指数给出了具有最小度条件的简单连通图是泛圈图的充分条件,其中Wiener指数、hyper-Wiener指数的充分条件优化了文献[15]中的结论。 记NP1={K2∨(Kn-4+2K1),K5∨6K1,K3∨(K2+3K1),K3∨(K1+K1,4),K3∨(K2+K1,3),(K2∨2K1∨5K1,K4∨5K1,K1,2∨4K1,K2∨(K1+K1,3),K3∨4K1}。 记NPC={K4∨5K1,K2∨(K3+2K1),K3∨4K1,K1,2∨4K1,K2∨(K1+K1,3),K2∨(K2+2K1),K1∨2K2,K2∨3K1}。 定理2.1设简单连通图G的顶点数为n(n≥5),δ(G)≥2。若 W(G) 则G要么是一个泛圈图,要么是一个二部图,要么属于NP1。 于是有 =n(n-1)-m 这与条件W(G)矛盾。 下面讨论G∈NP1的情况: 综上,当G∈NP1时,有W(G) 故G是一个泛圈图,或是一个二部图,或属于NP1。 推论2.2设G为n(n≥9)阶简单连通图,δ≥2,如果 W(G) 则G是一个泛圈图,除非G是一个二部图或G∈{K4∨5K1,K3∨4K1}。 定理2.3[15]设G为n阶简单连通图,δ≥2,如果 W(G) 则G是一个泛圈图,除非G是一个二部图或G∈NPC。 注:由于{K4∨5K1,K3∨4K1}⊂NPC,故n≥9时,定理2.1推广了定理2.3。 则G要么是泛圈图,要么是一个二部图。 于是有 则G是一个泛圈图,除非G是一个二部图。 定理2.6设简单连通图G的顶点数为n(n≥5),δ(G)≥2。若 WW(G) 则G要么是一个泛圈图,要么是一个二部图,要么属于NP1。 于是有 这与所给条件WW(G)矛盾。 下面讨论G∈NP1的情况: 综上,当G∈NP1时,有WW(G) 故G是一个泛圈图,或是一个二部图,或G∈NP1。 推论2.7设G为n(n≥9)阶简单连通图,δ≥2,如果 WW(G) 则G是一个泛圈图,除非G是一个二部图或G∈{K4∨5K1,K3∨4K1}。 定理2.8[15]设G为n阶简单连通图,δ≥2,如果 WW(G) 则G是一个泛圈图,除非G是一个二部图或G∈NPC。 注:由于{K4∨5K1,K3∨4K1}⊂NPC,故n≥9时,定理2.6推广了定理2.8。 则G要么是一个泛圈图,要么是一个二部图。 于是有 则G是一个泛圈图,除非G是一个二部图。 定理2.11设简单连通图G的顶点数为n(n≥5),δ(G)≥2。若 则G要么是一个泛圈图,要么是一个二部图,要么属于NP1。 于是有 下面讨论G∈NP1的情况: 故假设不成立,则G是一个泛圈图,或是一个二部图,或G∈NP1。 则G要么是泛圈图,要么是一个二部图。 于是有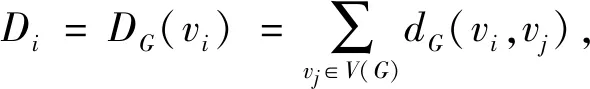
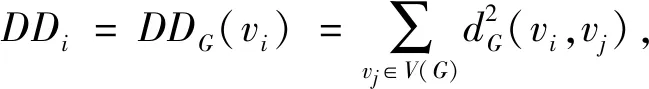
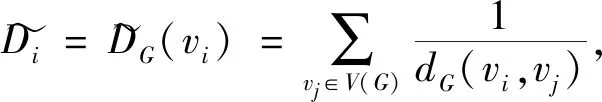
1 相关引理
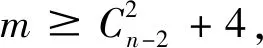
2 主要结论