Fq2上的几类置换多项式

周方敏

(肇庆学院 数学与统计学院,广东 肇庆 526061)

1 概 论

引理1设k为正整数。当s=ε或-ε/3时,下式恒为0,

(1)

证记式(1)中第1个和式为T1(k),第2个和式为T2(k)。由

T1(1)-εT2(1)=(-2b2)-ε(b-3b3)=εb(1+3εb)(1-εb)=0,

T1(2)-εT2(2)=(144b4-192b6)-ε(-3b-45b3+315b5-315b7)

(2)

=3εb(3b+ε)(b-ε)(35b4+2εb3-22b2+2εb-1)

=0,

知式(1)在前两个初始值处取值为0。

使用Zeilberger算法[5],[6]101-118,可以找出T1(k)和T2(k)所满足的递推关系。当b=ε时,

Ti(k+2)+Ti(k+1)-8(2k+1)(4k+5)2Ti(k)=0,i=1,2。

当b=-ε/3时,

27Ti(k+2)+(288k2+432k+184)Ti(k+1)+192(2k+1)2k2Ti(k)=0,i=1,2。

可见在这2种情况下,T1(k)和T2(k)均满足相同的2阶递推关系。故式(1)恒为0。

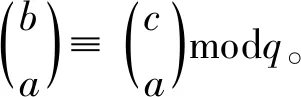
证不妨设b≥c且b=c+kq。在Fq[x]中,(1+x)b=(1+x)c(1+x)kq=(1+x)c(1+xq)k。比较上式中xa的系数即得所要的等式。

进行屋顶的防渗漏施工时，首先要选择合适的防水卷材，施工使用的防水卷材必须要符合国家房屋施工标准，其次在选择防水卷材时，要充分考虑当地的气候条件和其他外部因素，以此来选择合适的防水材料型号。在施工前，一定要查好防水卷材的各项指标，进行施工时一是要分区域进行合理的划分，分区域铺设防水卷材避免受力不同导致防水卷材出现开裂等问题，还要注意的是处理好防水卷材的衔接处，衔接处留够距离，避免出现衔接处渗漏问题。

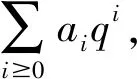
引理3[8]271Fq2[x]中的多项式f(x)是Fq2上的置换多项式的充分必要条件是

(3)

2 主要定理及其证明

(4)

先证明q为奇数。因为若q为2的方幂,则由

得t=0,这与定理假设不符。

从式(4)可以看出,当q2-1|/2i(q-1)+k,即2(q-1)|/k时,Sk=0。因此我们只需要计算S2k(q-1)(k=1,2,…,(q-1)/2)的值,

[必要性]

若f(x)为Fq2上的置换多项式,则

当q=3时,-S2q-2=4t+4t3=4t(1+t2)=0,得s=t(q+1)/2=(-1)(q-1)/2=ε。当q>3时,

当Fq2的特征为3时b=ε,当Fq2的特征大于3时b=ε或-ε/3。

[充分性]

在上述和式中,0≤i≤2k-1,0≤j≤q-2k,因此-(q-3)/2<1-k≤k+j-i≤q-k

(其中第2个等号的计算需要用到引理2。)因此,

因此,

根据引理1,上式右端恒为0,故Sk(q-1)=0。因此当k=0,1,…,q2-1时,Sk=0。

下证f(x)=x(1+tx2(q-1))在Fq2中只有平凡零点,从而Sq2-1=-1。若x≠0为f(x)的零点,则t=-x2-2q,s=t(q+1)/2=(-1)(q+1)/2x1-q2=-ε,因此ε=-ε或-ε/3=-ε,但Fq2的特征不为2,这两种情况都不成立。

定理2设s,t∈Fq,N(x)=x1+q,则f(x)=x(s+tN(x)+N(x)2)为Fq2上置换多项式的充分必要条件是:s=t=0;或5|q,t=0且-s不是Fq中的完全平方。

证由引理1.2[7]及如下交换图表可知,

f(x)为Fq2上置换多项式的充分必要条件是x(s+tx+x2)2是Fq上的置换多项式。

而x(s+tx+x2)2是Fq上的置换多项式的充分必要条件是:s=t=0;或5|q,t=0且-s不是Fq中的完全平方。[8]352