多边形内角和、外角和定理专练

考点梳理

一、内角和与边数结合

此类题主要是已知边数求内角和，或者已知内角和求边数.

例1 （1）一个多边形的边数是10，求这个多边形的内角和；（2）一个多边形的内角和是1260°，求这个多边形的边数；（3）两个多边形的边数之比为1∶2，内角和之比为1∶3，求两个多边形的边数.

解析：（1）已知边数为10，由多边形内角和定理可得内角和为（10 - 2） × 180° = 1440°.

（2）已知多边形的内角和为1260°，设边数为n，则180°（n - 2） = 1260°，解得n = 9.

（3）根据两个多边形边数之比为1∶2，可设这两个多边形的边数分别为n和2n，因为内角和之比为1∶3，则3 × （n - 2） × 180° = （2n - 2） × 180°，解得n = 4，则2n = 8.因此，这两个多边形的边数分别为4和8.

二、内角和与外角和结合

解此类题的关键是明确多边形的外角和为360°这个隐藏的已知量.

例2 一个多边形的内角和等于外角和，求这个多边形的边数.

解析：由（n - 2） × 180° = 360°，可得边数n = 4.

三、内角和与方程、不等式等知识结合

例3 一个多边形除一个内角外，其余内角之和等于1000°，求多边形的边数和除去的那个内角的度数.

解析：多边形每个内角的取值范围都是大于0°且小于180°，除去的这个内角的度数等于这个多边形的内角和减去其余内角之和，列不等式为0° lt; （n - 2） × 180° - 1000° lt; 180°，解得n = 8.也可以利用方程（x" - 2）·180° = 1000°，解得 x ≈ 7.5，所以这个多边形的边数是8，除去的这个内角为1080° - 1000° = 80°.

四、正多边形中内角、外角与边数结合

正多边形的内角相等、边相等.常见的考查类型有：已知边数求内角；已知内角求边数；已知外角求边数.

例4 （1）求正十五边形的每个内角的度数；（2）一个正多边形的一个内角为144°，求这个正多边形的边数和内角和；（3）一个正多边形的一个外角是45°，求这个正多边形的边数和内角和；（4）小明从 A 点向东走10米后，向右转20°，再向前走10米，如此往复，当小明第一次回到 A 点时，求小明此时走的总路程.

解析：（1）正十五边形的每个内角为156°.

（2）这个正多边形的边数为10，内角和为1440°.

（3）这个正多边形的边数为8，内角和为1080°.

（4）已知条件中并没有直接告诉我们这是一道正多边形问题，而小明从 A点出发一直走下去，直至第一次回到出发点 A 时停止，所走的路径为正 n 边形.由题意得20°n = 360°，则 n = 18.小明所走的总路程是18 × 10 = 180（米）.因此，小明所走的总路程是180米．

分层作业

难度系数：★★★ 解题时间：3分钟

1.小明从A点向东走x米后，向右转30°，再向前走x米，如此往复，当小明第一次回到P点时，小明一共走了240米，求x.（答案见本页）

难度系数：★★★ ★ 解题时间：4分钟

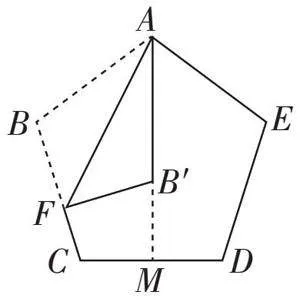
2.如右图，将正五边形纸片[ABCDE]折叠，使点[B]与点[E]重合，折痕为[AM]，展开后，再将纸片折叠，使边[AB]落在线段[AM]上，点[B]的对应点为点[B]'，折痕为[AF]，求[∠AFB]'的大小．（答案见本页）

（作者单位：沈阳市第一四五中学）