不同电极数石英谐振器集群力敏特性分析
2019-11-20田文杰陈福彬
田文杰,陈福彬,佟 盟,冯 洁
(1.北京信息科技大学传感器重点实验室,北京 100101;2.云南师范大学物理与电子信息学院,昆明 650500)
石英晶体是一种高稳定性的各向异性压电材料,广泛应用于频标及数字化信息处理领域。由于石英晶体的各向异性,由石英晶体构成的元件特性(如力敏特性、温度特性等)与晶体的切割方式(即切型)密切相关,即石英晶体的切型及振动模态与应用领域相关[1-4]。在石英晶体力敏特性应用领域常用的是AT 切。这种切型不仅有较好的力敏特性,而且有较宽的频率温度稳定性,在石英数字式力传感器及惯性器件开发应用领域倍受人们的关注[5]。但在传统的基于两个单电极石英谐振器配对使用的过程中,如何克服温度特性引起的慢性漂移一直是石英力敏谐振器在应用领域难于解决的瓶颈问题[6-9]。因此,本文针对石英材料温度特性及应用环境因素对石英力敏特性应用过程的干扰问题,根据石英晶体的压电效应,在分析晶体谐振频率与晶体结构参数关系的基础上,用MATLAB 数值计算方法,计算了石英晶体薄圆片受径向力作用时,晶片内各点的应力数值变化及分布情况。根据晶体振动的能陷理论、波在晶体中的传播特性及力作用对晶体谐振频率的影响,设计并制作了不同基频及不同电极数的集成式石英力敏谐振器集群,并将同一晶体基片上的不同位置的谐振器的谐振频率进行差频处理,以此抑制晶体材料因素对谐振频率的干扰,再将得到的差频信号进行叠加处理,达到提高谐振器集群力-频转换系数的目的。
1 石英晶体的力敏感机理
石英晶体为SiO2,由于原子的特殊排列结构,构成了石英晶体的特殊性质。这种性质与晶体的轴向相关,轴向不同对应的特性不同,此即石英晶体的各向异性特性。压电特性是石英晶体最显著的特性,也是石英元件得到广泛应用的基础。
晶体的压电特性体现了晶体应力T、应变S、电场E、电位移D之间的相互作用,这种关联关系可用四类压电方程来描述。压电方程不同,对应的变量及应用领域不同。对于利用石英晶体压电特性的力敏谐振器,晶体一般工作于高频谐振状态,压电方程选应变S和外加电场E为自变量,应力T及电位移D为因变量。所以,压电方程为
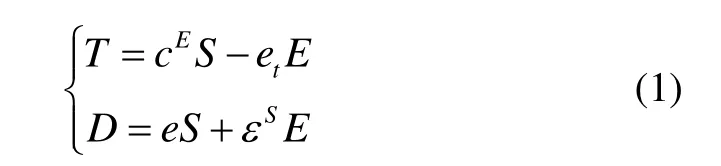
式中,c是弹性刚度常数,e是压电应力常数,ε为介电常数,et为e的转置矩阵。
对于长、宽、厚分别为a、b、d的大薄片石英晶体(a,b>>d),在电场激励作用下,晶体谐振频率[5]为

式中,m、n为奇实数,c55、c66为弹性刚度常数分量,ρ为晶体密度。由式(2)知,晶体谐振频率主要由厚度、晶体密度及刚度常数分量决定。
当晶体受力F(单位厚度上的力,量纲N·m-1)作用时,晶体的内应力将使结构参数(c、d、ρ)产生微量变化,从而导致晶体的谐振频率发生改变Δf。由于石英晶体具有各向异性特性,晶体谐振频率的变化Δf不仅与力作用F的大小有关,而且与力作用的方位(方向)ψ有关。它们之间的关系可用力灵敏度系数Sf(ψ)表示为

对于薄圆形晶片,在直径方向施加径向力F时,晶体内P点的应力与F间的关系可用如图1所示的模型来描述。
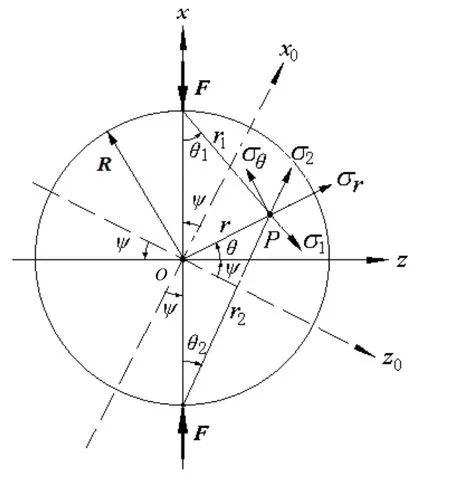
图1 径向力作用下薄圆片晶体的应力模型 Fig.1 Stress model of thin wafer under radial force
图1中,xoz为力作用坐标系,ox轴与力F共线;x0z0为晶体坐标系。对于AT 切石英薄片,ox0轴为晶体的电轴,ψ为力作用方位角(即作用力方向与ox0轴的夹角)。在F的作用下,晶片内P点产生的两个分应力σ1、σ2为

式中,λ、μ为由边界及力平衡条件决定的参数(量纲N·m-1),α、β、γ、δ为由晶体弹性柔顺常数张量矩阵元素决定的材料常数(无量纲。晶体弹性的各向异性就体现在这些材料参数上)。
对At 切石英晶体,

所以,晶片内P点的应力应为两个分应力σ1、σ2之合。为简化方程需要,引入极坐标系,并将P(r,θ)点的应力σ1、σ2投影到r、θ方向即可得到极坐标系下P点的正应力σr、σθ及切应力τrθ。
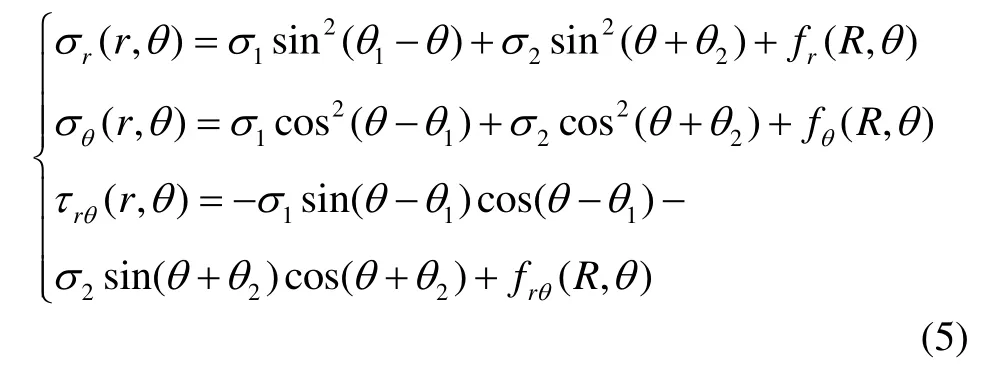
式中fr(R,θ)、fθ(R,θ)、f rθ(R,θ)为由边界条件确定的附加补偿函数(可由r=R时,晶体边界自由,即σr(R,θ)= 0、σθ(R,θ)=0 及τr θ(R,θ)=0,反推求得)。
2 数值计算
晶体受径向力作用时,内部的应力分布由式(5)进行描述,但解析式极为复杂。可用MATLAB 数值计算及ANSYS 有限元方法进行模拟分析。
在径向力作用下,对于AT 切石英薄圆片,可得到中心点P(0,0)的应力σr(0,0)、σθ(0,0)、τrθ(0,0)与方位角ψ之间的解析式为:

式(6)可用图2描述。
用MATLAB 数值计算软件进行空间应力计算,可得到直观的应力分布三维图。MATLAB 数值计算程序的编制方法如下:
1)设定结构参数R及状态量F、ψ;
2)根据晶体材料的柔顺常数矩阵、晶体的切型及加力F、方位角ψ,计算得到材料参数α、β、γ、δ及对应晶体切型的λ、μ;
3)根据式(4)(5)求出σr、σθ、τrθ。

图2 圆片中心应力与加力方位角的关系 Fig.2 Relationship between stress at center of wafer and azimuth angle of applied force
所以,对半径R=7 mm 的AT 切石英晶体薄圆片,在径向力F(=1 N)与x0轴方向的夹角即方位角为ψ时,用MATLAB 数值计算得到的应力在xoz平面内的分 布如表1所示。径向力作用下,内部应力分布可近似用六次函数式描述。
晶体边缘力作用点附近的应力σr与加力方位角的关系如图3所示,应力的大小相对于ψ=90°即oz0轴对称。因此,在径向力作用下,薄圆形晶体片上的不同位置,其对应的应力变化差异较大。若在薄圆片上的不同位置设置谐振器时,相应的力敏特性也将存在较大差异,而且与力作用方位存在密切的关系。
在径向力作用下,同一晶片不同位置晶体应力变化的ANSYS 有限元分析结果与对应点的谐振器的力灵敏度系数的关系研究参见文献[10]所述。

图3 径向力(F=1 N,R =7 mm)作用下,晶体边缘力作用点的σr 与ψ 的关系 Fig.3 Relationship between σr at wafer edge and the azimuth ψ under radial force (F=1 N,R =7 mm)

表1 径向力(F=1 N,R =7 mm)作用下,应力分布与加力方位角的关系 Tab.1 Relationship between stress distribution and azimuth under radial force (F=1 N,R =7 mm)
3 多电极谐振器集群结构
在分析径向力作用下石英晶片内应力分布的基础上,以晶体表面为对称面在晶片不同位置设立电极,以构成多个独立的谐振器。这些谐振器因在晶片上所处的位置不同,同一径向力作用时,对应的应力变化不同,因此,相应的力灵敏度系数Sf也不同。若将各谐振器的谐振频率彼此间进行差频处理,根据同基晶体谐振器谐振频率信号的共模抑制原理,可抑制晶体材料因素对谐振频率的影响,即得到的差频信号中,力敏特性仍然存在,但材料的温频特性及工艺差异等因素引起的干扰得到了抑制[11]。这就是谐振器差频应用的基础。据此设计的三电极、四电极、六电极谐振器结构如图4(a)(b)(c)所示,谐振器上下电极引线各自错位独立,以避免引线对谐振器振动模态的干扰。
图4中,晶片直径为14 mm,图4(a)(b)对应的三电极、四电极谐振器晶片厚度约为0.166 mm,图4(c)六电极谐振器晶片厚度约为0.083mm。各谐振器电极中心位置均匀分布于与晶片同心、半径为4 mm 的圆周上。谐振器的电极直径∅及电极引线宽度h分别为:三电极∅=3 mm、h=1.2 mm,四电极∅=3 mm、h=1.2 mm,六电极∅=1 mm、h=0.5 mm。谐振器电极及电极引线可用Pt、Au、Cu、Al 等金属材料,采用蒸镀或沉积 的方法进行制备。其中,以Au 为电极材料,采用蒸镀方法得到的三电极、四电极、六电极谐振器实物图片如图5(a)(b)(c)所示(蒸镀电极时,先用铬Cr 打底,厚度200 Å,再镀Au 2700 Å)。谐振器电极引线再用弹簧连线(图5(d)所示)与激励电路连接。
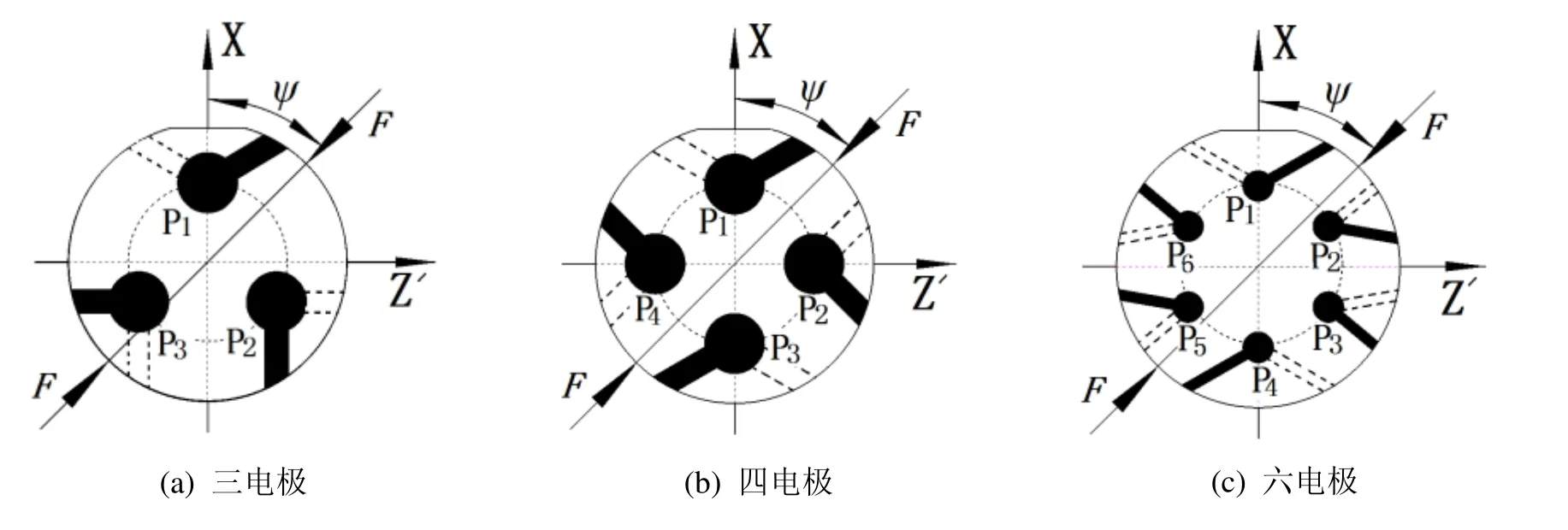
图4 谐振器电极位置结构设计 Fig.4 Position design of resonator electrodes

图5 谐振器实物图片 Fig.5 Picture of resonator
4 谐振器的力敏特性
将不同位置的谐振器与对应的激励电路连接,并使各个谐振器独立工作于基频状态,如图6所示(谐振器采用晶体振荡器模块SM5009(系列)驱动,电源选用高效线性稳压模块AMS1117(系列),它们的工作温度为-40℃~85℃,存储温度-65℃~150℃,温度测试时可将负温扩展到-55℃测量)。用实验室设计的径向加力装置,如图7(b),在砝码托盘上通过加、减砝码的方式在沿晶体的x轴方向(ψ= 0°)施加径向力(为防止加力时晶片脆裂,在晶片与力作用点间垫一层厚约0.2 mm 的薄膜),并用Agilent-53132A 型数字式频率计(10 位半)测量径向力变化时对应的谐振器谐振频率,并计算频率变化量,测试过程如图7所示。得到的三电极、四电极、六电极谐振器集群的力敏特性关系如图8(a)(b)(c)所示。

图6 六电极激励电路及力敏特性测试原理 Fig.6 Six-electrode excitation circuit and principle of force sensitive test

图7 谐振器力敏特性实际测试过程示意图 Fig.7 Diagram of testing process of resonator force sensitivity
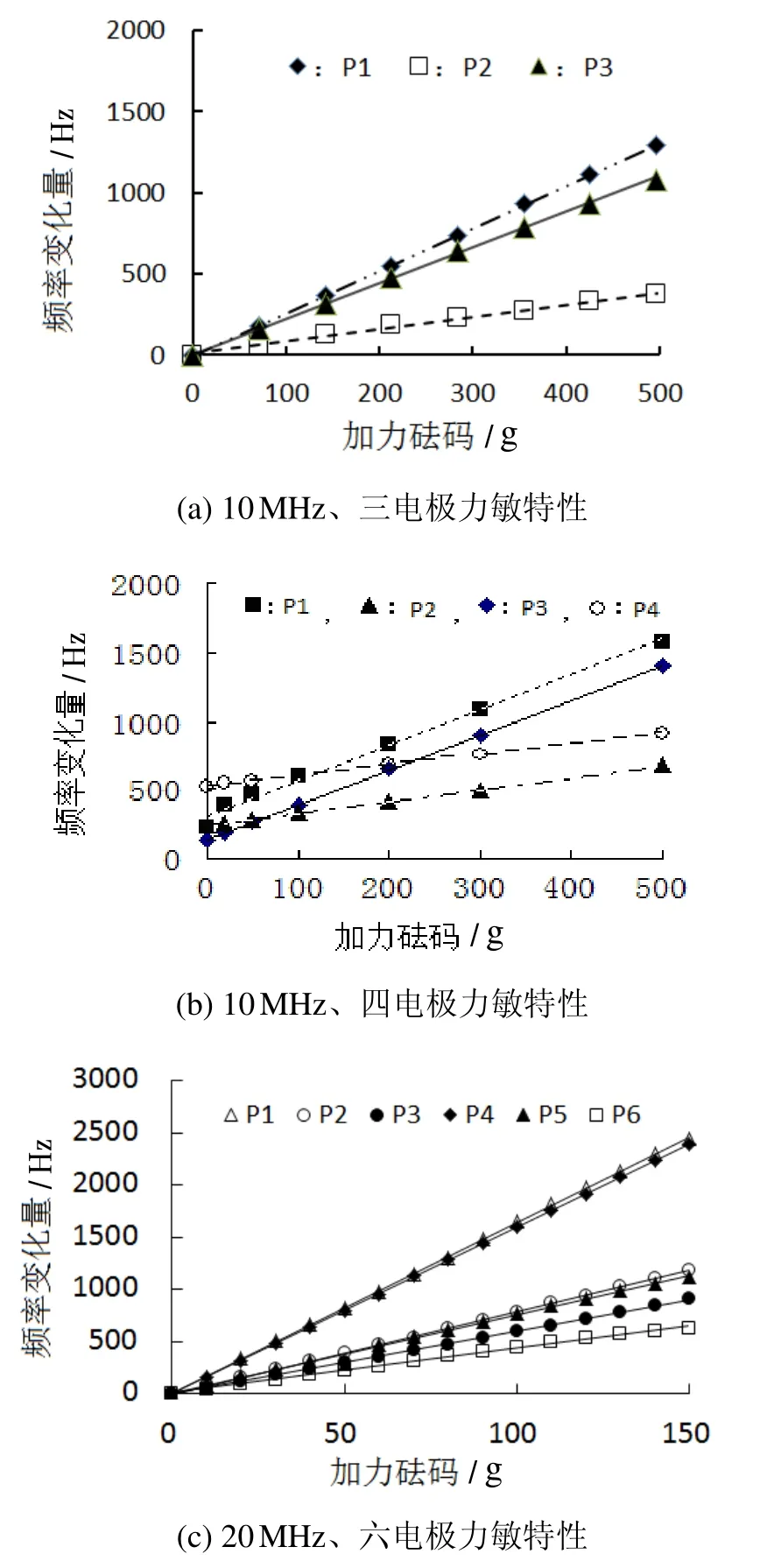
图8 多电极谐振器集群的力-频敏感特性关系 Fig.8 Force-frequency sensing characteristics of multi-electrode resonator
由图8(a)(b)(c)的力敏特性曲线可知,同一晶片不同位置的谐振器对应的力灵敏度系数Sf差异较大,且谐振频率为20 MHz 的谐振器比10 MHz 谐振器具有更高的力灵敏度系数。若将各谐振器的谐振频率彼此间进行差频处理,则差频信号中力敏特性仍然存在,而干扰因素将得到抑制。若将得到的多个差频信号进行叠加处理,则可有效地提高谐振器集群的力敏感特性,同时进一步改善输入-输出线性关系。
5 频率信号差频及叠加融合
对图4、图5所示的谐振器集群结构,用ki-j表示电极i与电极j对应的谐振器的差频的力-频转换系数(即变化的单位力所对应的频率变化量),kijl表示电极i、电极j、电极l之间彼此差频后再叠加求和得到的力-频转换系数,则对图4(a)、图5(a)所示的10 MHz三电极谐振器集群结构及图8(a)对应的力敏特性,在ψ= 0 时,可将P1与P2、P1与P3、P3与P2作差频处理,其差频信号对应的力-频转换系数为k(P1-P2)≈250 Hz/N,k(P1-P3)≈130 Hz/N,k(P3-P2)≈120 Hz/N(将图8中的加力砝码换算为力,在北京地区1 克(g)砝码对应的力= 9.8015×10-3N)。若再将得到的三个差频信号作叠加融合,则叠加信号的力-频转换系数k(123)可达到约500 Hz/N。
对图4(b)、图5(b)及图8(b)所示的10 MHz 四电极谐振器集群及力敏特性,在ψ= 0 时,可将差异较大的P1与P2、P4,P3与P2、P4进行差频处理,对应的力-频转换系数k(P1-P2)≈170 Hz/N,k(P1-P4)≈174 Hz/N,k(P3-P2)≈177 Hz/N,k(P3-P4)≈180 Hz/N。若再将k(P1-P2)、k(P1-P4)、k(P3-P2)、k(P3-P4)作叠加融合,则叠加信号的力-频转换系数k(1234)可达到约701 Hz/N。
对图4(c)、图5(c)及图8(c)所示的20 MHz 六电极谐振器集群及力敏特性,在ψ= 0 时,用同样的方法,将差异较大的P1与P2、P3、P5、P6,P4与P2、P3、P5、P6,P2、P5与P6进行差频处理,其对应的力-频转换系数为:
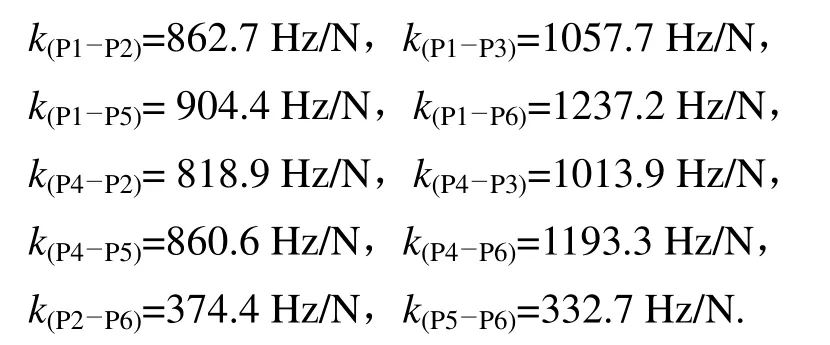
若将所得结果再进行叠加求和,则最终叠加信号的力-频转换系数k(123456)可达到8655.8 Hz/N。
由以上实验结果得,对同基多电极石英力敏谐振器,采用差频及差频信号叠加方法,可有效提升谐振器最终频率信号的力-频转换系数。在允许的情况下,同一基片集成的谐振器的数量越多,可选择的差频配对形式越多,再经叠加求和后对谐振器集群整体的力-频转换系数的提升效果越好;同时,谐振频率越高,力-频转换系数越大,差频及叠加后对力-频转换系数的提升效果越明显。
6 温度漂移抑制
从材料结构角度,石英晶体谐振频率的温度特性,与晶体的切型密切相关。对AT 切型的石英晶体,切角产生1′的误差时,与之对应的频率-温度系数平均值将产生10-7/℃的变化。 因此,对于同一切型的晶片,切角及工艺误差对晶体谐振频率的温度特性影响十分明显。但对同一晶片而言,在晶片平面不同位置的谐振器,它们的频率-温度特性应该是完全相同的,若将这些不同位置的谐振器的谐振频率进行差频处理,温度的干扰将得到抑制,甚至被完全消除,此即本文差频处理的核心目的。但由于谐振器电极制备、激励电路等因素的影响,同一晶片不同位置的谐振器的谐振频率温度特性规律基本相同,但仍存在微小差异。
谐振器的谐振频率温度特性测试示意如图9所示。先将谐振器封装于玻璃瓶内并与激励电路连接,再将谐振器及电路置放于高低温试验箱内,接通电源及数字式频率计。让高低温试验箱降温致-55℃并保存30 min后,在-55℃~+70℃的范围内,温度每隔10℃,相邻温度点过渡时间15 min,并在测试点再稳衡15 min 后用频率计测试不同位置谐振器的谐振频率,实验过程如图10所示。不同位置的谐振器的频率温度特性的测试结果如图11 所示。将不同位置的谐振器的谐振频率作差频处理,得到的差频信号的频率温度特性如图12 所示。
比较图11、图12 的结果可知,在-55℃~70℃范围内,差频前温度引起的频率变化量约800 Hz,而差频后的频率变化量约300 Hz。差频后,温度对频率信号的影响得到了一定程度的抑制。
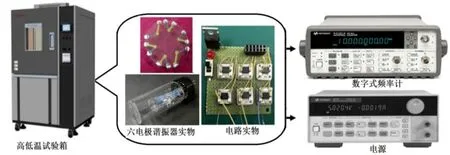
图9 谐振器谐振频率温度特性测试示意 Fig.9 Test of frequency and temperature characteristics of resonator

图10 谐振器谐振频率温度特性测试过程示意图 Fig.10 Diagram of testing process of frequency and temperature characteristics of resonator

图11 同一晶片不同位置谐振器的温频特性 Fig.11 Temperature-frequency characteristics of resonators at different positions on the same wafer
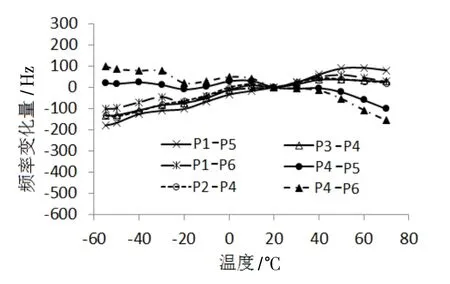
图12 差频信号的温频特性 Fig.12 Temperature frequency characteristics of beat frequency signals
7 实验结果分析
在一定的力作用方式下,谐振器的力敏特性,与谐振器的基片厚度(决定谐振频率)及谐振器在基片上所处的位置有关。根据图8所得结果:三电极(10 MHz)和四电极(10 MHz)谐振器的力敏特性明显低于六电极(20 MHz)的力敏特性;而处于三电极P1位置、四电极P1和P3位置、六电极P1和P4位置的谐振器,其力敏特性较其它位置的谐振器力敏特性显著,且经差频处理后,基频较高的谐振器(20 MHz),其差频信号的力敏感特性也较高;叠加处理后,20 MHz六电极谐振器集群的力-频转换系数(8655.8 Hz/N)分别是三电极谐振器集群(500 Hz/N)的17.3 倍,是四电极谐振器集群(701 Hz/N)的12.3 倍。由图11~12的实验结果,一方面说明了同一基片上不同位置的谐振器的频率温度特性变化规律的相同(或相似)性,另一方面说明谐振器频率温度特性不仅与晶体的切型有关,而且还与谐振器的制备、激励电路、电极位置等因素有关,成因复杂。因此,解决谐振器温度干扰是谐振器在高精度测试应用领域存在的瓶颈难题。但实验表明,通过差频处理,能有效地抑制温度的干扰,若再将同一基片上的多个差频信号进行叠加融合,则可提高整个晶片(谐振器集群)的力敏感特性。
8 结 论
基于同一晶体基片的谐振器,其力敏特性与谐振器所处的位置、谐振频率及力作用方位有关。在一定方位的径向力作用下,将不同位置的谐振器的谐振频率进行差频处理得到的差频信号仍具有较好的力敏特性,但得到的差频信号其温度及材料等因素引起的干扰得到了较好地抑制。若将得到的差频信号进行叠加融合,则可进一步提高谐振器整体的力敏特性(用力-频转换系数描述)。在允许情况下,同一晶体基片上的电极数越多,即谐振器越多,则谐振器间可选择的配对形式越多,整体力-频转换系数的提升效果越好;谐振频率越高,差频及叠加信号的力-频转换系数的提升效果越明显。测试结果表明:对于设计的10 MHz 三电极谐振器集群,差频信号经叠加处理后,其力-频转换系数可达500 Hz/N;对10 MHz 四电极结构的谐振器集群,其力-频转换系数可达701 Hz/N;而对20 MHz六电极结构的力敏谐振器集群,最终输出信号的力-频转换系数可达8655.8 Hz/N(是三电极谐振器的17.3倍、四电极谐振器的12.3 倍)。在-55℃~70℃范围内,差频前温度引起的频率变化量约800 Hz,差频后的频率变化量约300 Hz。经差频处理,温度的干扰得到了一定程度的抑制。这种多电极集成式的力敏谐振器可用于高稳定的数字式力传感器及惯性敏感元件或姿态检测控制系统。
