基于顺序统计量的加速度计恒加寿命试验优化设计

赵晓东，穆希辉

（1.陆军工程大学 石家庄校区，石家庄 050003；2.特种勤务研究所 石家庄营区，石家庄 050003）

某型远程制导火箭弹作为我军远程精确打击的重要力量，具有长期贮存、一次使用的特点，加速度计作为其长期贮存中的薄弱环节[1]，准确评估加速度计的贮存寿命是关乎该远程制导火箭弹制导精度和作战效能发挥的重大问题。加速度计是长寿命、高可靠性产品，要在较短时间内评估其贮存寿命，必须开展加速度计的加速寿命试验和分析[2]。

与步进和序进寿命试验相比，恒加寿命试验应用最为广泛，试验与评估技术也最为成熟，具有方法简单和结果准确的优点，但其存在着样本量大和试验时间长的问题。为改进恒加寿命试验，有些研究者对恒加寿命试验的优化设计问题进行了研究。陈文华[2]对双应力的恒加寿命试验的优化设计问题进行了研究；沙美妤[3]采用极大似然估计法对球轴承的恒加寿命试验进行了优化设计；Duan[4]通过伽马过程对单应力的恒加退化试验方案进行了优化设计；Wang[5]使用M 最优法则对恒加试验方案进行优化设计；Gao[6]将多应力转化为单应力，对恒加寿命试验优化设计问题进行了探讨。但上述优化设计都是在模型参数先验信息已知的情况下，对恒加寿命试验方案进行的优化设计，同时，其多以产品正常使用应力水平下的一个P 分位寿命的渐近方差最小为优化目标，具有一定的局限性[7]。

针对上述问题，本文基于顺序统计量和整体线性无偏估计理论，以每个应力水平下的样本分配为设计变量，同时以加速度计在正常应力水平下中位寿命估计值的方差最小和模型参数的协方差阵行列式最小为优化目标，建立加速度计定数截尾恒加寿命试验优化设计的数学模型，对加速度计的恒加寿命试验方案进行了优化设计。

1 加速寿命方案

1.1 加速度计预实验

在加速度计加速贮存试验设计之前，需开展加速预试验作为加速贮存摸底试验，得到的试验信息主要包括以下三点：

1）确定加速度计的可加速性；

2）确定加速度计加速退化应力水平上界；

3）确定加速度计性能参数是否存在退化规律。

依据该型加速度计的贮存规范（温度小于30℃，湿度小于70%RH）推断其在贮存过程中敏感应力主要包括温度和湿度，因此选择温度、湿度为加速试验的应力类型。

预试验共开启2 个温湿度试验箱进行试验，一个为温度单应力试验，一个为恒湿（75%RH）温度双应力步进应力试验。试验过程中的试验箱运用说明如下：

A 试验箱进行高温步进应力加速试验，温度应力依次为：S1=70℃，S2=85℃，S3=95℃，S4=105℃，S5= 110℃；

B 试验箱进行恒湿（75%RH）温度步进应力加速试验，温度应力依次为：S1=70℃，S2=85℃，S3=95℃，S4=105℃，S5=110℃。

当B 试验箱温度应力高于95℃时无法施加湿度条件，直接将B 试验箱中的样本拿到A 试验箱，一并进行S4=105℃，S5=110℃试验。

用5 个同批次的加速计新品作为试验样品，进行35 天不间断试验。另根据人机功效最大化原则，在温度应力S1、S2、S3、S4下各试验、测试7 天，如果还有样品没有失效，则继续放在S5下进行试验。每一应力水平下试验时间包括应力持续时间、加速度计检测时间以及升温降温时间。

通过专用的检测设备，采用定周期检测方法进行加速度计失效时间的测量，每周检测3 次，分别在每周的第2 天、第5 天和第7 天（即改变应力水平时）开始检测程序：进行检测时，需将加速度计恢复在正常应力水平S0（室温25℃）下进行检测，以保证测试条件的一致性。

试验的终止条件如下：1）加速度计发生不可修复故障；2）加速度计出现故障，如果确认该故障在其使用过程中不可能出现，或者出现故障的应力水平远高于其技术规范极限且确保已有足够的安全余量，则可终止试验；3）试验温度长时间（大于15 天）稳定在110℃而无失效样本产生，可终止试验。

按照上述试验方案，进行加速度计的预实验，其失效分布如图1所示。

加速计的具体失效情况如表1所示。

图1 加速度计预试验失效分布图 Fig.1 Distribution of accelerometer pre-test failures

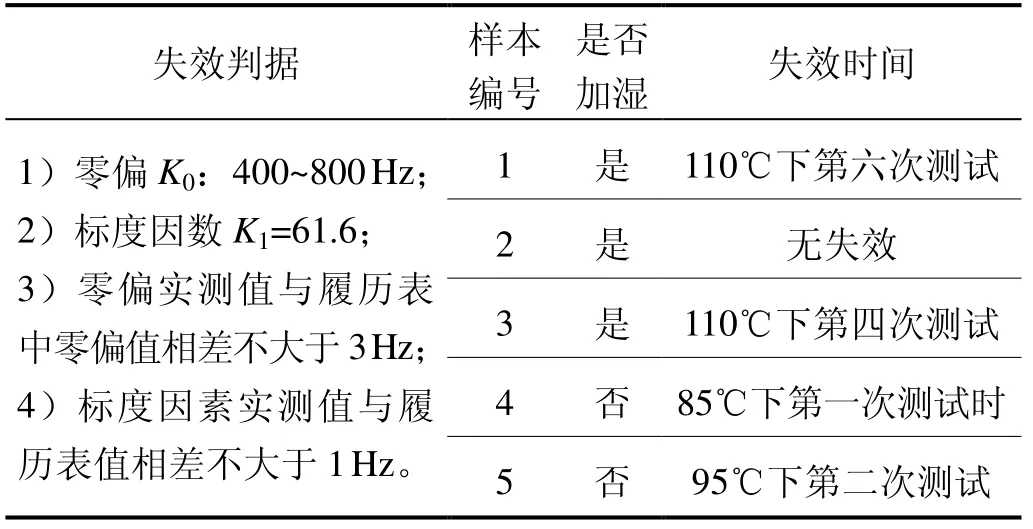
表1 加速度计预试验失效情况表 Tab.1 Failures in accelerometer pre-test

从图1和表1中可以看出，4 次失效分别发生在85℃（1 个）、95℃（1 个）以及110℃（2 个）下，对失效的样本进行了失效分析。结果显示，预试验中1 号和4 号样品输出异常，3 号和5 号样品超差。分析结果同自然贮存中加速度计的故障形式一致，说明加速度计具有显著的可加速性。

对发生故障的4 台加速度计进行故障分析，确定4 台加速度计发生故障的部位均为敏感头，其中输出异常是由于敏感头摆片组梁断和腹带松动造成，超差均是由于敏感头腹带松动造成，所以加速度计虽然两种失效模式不同，但其失效原因基本一致，故后续的数据分析都基于一种失效模式展开。另外，加湿环境中加速度计的失效模式与不加湿环境中加速度计的失效模式相同，且加湿环境中加速度计的失效均发生在110℃的高温下，此时湿度已经无法保证，因此，湿度应力并不是加速度计失效的关键应力。

1.2 加速寿命模型

根据加速度计预试验的结果，以及其自然贮存数据的分析结果[1]发现，湿度对于加速度计寿命的影响从数据规律上难以体现，无法定量刻画。所以，试验应力仅采用温度应力作为加速应力。

由于确定温度应力为加速应力，因此选择Arrhenius 模型作为加速模型。Arrhenius 模型表明寿命特征随着温度上升而按指数下降，对模型取对数可得：

其中，ξ表示产品的特征寿命，T为温度应力，a和b为待定的参数，ε为测量误差，寿命特征的对数是温度倒数的线性函数。

1.3 加速系数预估

依据加速度计的自然贮存寿命[1]分析结果，威布尔函数和I 型极大值分布函数可以作为加速度计的分布函数。经分析[8]，根据加速系数的定义，I 型极大值分布没有可加速性，故选择威布尔函数作为分布函数。在求得分布函数之后，根据加速度计在不同温度条件下的平均贮存寿命及可靠寿命，可以对加速系数进行估计。

设步进应力加速寿命试验共有k个应力，其中S0为常规应力水平。在应力Si下共有ri个产品失效，失效时间分别为：

其中，τi为Si下的截尾时间（即应力水平改变的时刻），

各应力水平下加速度计贮存寿命的分布函数为：

其中，mi和η i分别为应力Si下的形状参数和尺度参数，并作出以下基本假设：

假设I各应力水平Si下的形状参数mi相等；

假设II产品的特征寿命η i与所施加应力Si，满足Arrhenius 加速方程：

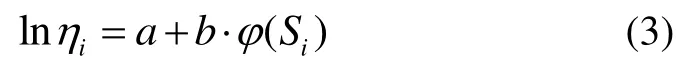
假设III产品剩余寿命仅依赖于失效累积量和当时的应力水平，而与累积方式无关。

由假定I 分布的形状参数mi相等，则应力Si下第j个失效样本的失效时间折算到给定应力Sq下的失效时间为：

到达试验截尾时间τk仍未失效的样本折算到给定应力水平Sq下的时间为：

其中，T q、Ti是应力水平S q、Si下的热力学温度，b是加速模型中确定的参数。

根据以上分析，可得似然函数如下：

通过解如下方程组：

结合加速度计的预试验失效数据，将加速度计失效时间折算到90℃，可以得到模型未知参数极大似然估计值如下：

据此，可得加速模型如下：

常温为25℃，如果加速寿命试验的温度应力分别选80℃、95℃、110℃、130℃，不难得到产品寿命均值的加速系数如下：

1.4 恒加试验方案

1.4.1 温度应力水平的确定

在恒加应力试验中，一般选择3～5 个应力水平进行试验[3]。本试验方案由于受到试验样本量较少，同时，由加速模型可以看出，模型的待估参数有3 个（阿伦尼乌斯模型中的参数a和b，威布尔分布中的形状参数m），所以试验数据的最小可解条件为3 个加速应力水平。因此，加速度计的加速寿命试验选择三个应力水平（S1＜S2＜S3）。

根据加速度计预试验结果和加速系数的预估结果，选择S1=80℃，S3=110℃，并根据温度应力倒数等间隔取值公式，确定S2。即：

1.4.2 试验样品的选取与分组

选取8 个同批次的新品加速度计，分配到已经确定的三个应力水平，具体的样本分配可以由试验的优化设计确定。

1.4.3 测定失效时间

根据加速度计的技术规范确定的失效标准，判断受试样品是否失效，并采用定周期测试方法，即预先确定若干个测试时间，

当ni个样品在应力Si下进行寿命试验到τi时，对受试验品逐个检查受试指标，判定是否失效，这样可以得到在检测周期 (τi-1,τi)内样品失效数li，而这li个失效产品的准确失效时间是无法获得的，这种情况称为定周期测试。用等间隔方式估计此li个失效样品在(τi-1,τi)内的失效时间，即取：

其中，τi、τi-1是检测时间，l i为检测周期内的失效数，h是时间（小时）。

检测时间由试验操作人员确定，在高应力水平下，试验的检测间隔应该较为致密，在低应力水平下，检测时间间隔可以相对疏松。

1.4.4 试验停止时间

由于试验样本只有8 个，总量较小，因此被测样本全部出现故障试验停止。

2 优化设计理论

与传统的极大似然估计法相比，基于顺序统计量的方法具有如下优点：

1）顺序统计量的部分性质不依赖于母体的分布并且计算量很小，使用起来比较方便，而且由于产品故障或寿命数据的时间性特点，在可靠性数据分析中，顺序统计量是一种非常重要的统计量；

2）将顺序统计量引入加速寿命试验优化设计中，运用整体最佳线性无偏估计理论，解决了模型参数先验信息未知情形下的优化设计问题；

3）对于样本量较小的寿命试验数据，综合利用不同应力间的横向信息，从而提高评估的精度。

2.1 模型假设

1）加速度计寿命在统计上相互独立[9-10]；

2）在任一应力水平下，加速度计寿命服从威布尔分布；

3）在各应力水平下，产品寿命分布的参数σ保持不变；

4）寿命分布的参数μ是应力的线性函数，即

其中，x= 1/T，模型参数a、b、σ由试验数据估计得到。

2.2 顺序统计量

设总体的密度函数为f(t)，分布函数为F(t)，T1,是总体的一个样本，其值为将其从小到大排列，则称为顺序统计量，T(n)称为该样本的最大顺序统计量，T(1)为最小顺序统计量。

2.3 最佳线性无偏估计

最常使用的极大似然估计方法只有在大样本情况下才具有良好的性质，整体最佳线性无偏估计方法综合利用不同应力间的横向信息，可以提高参数的估计精度。

加速度计寿命t服从威布尔分布，累计失效函数为：

其中，η为特征寿命，m为形状参数。

令y= lnt，则转化为I 型极小值分布，其累积失效函数为：

其中，位置参数μ= lnη，尺度参数σ= 1/m。

密度函数为

令y= lnt，极小值分布的前qj个顺序统计量分别

由于

所以

其中，εji服从均值0，标准差为σ的极小值分布为

分别对a、b、σ求偏导，得到以下三个线性方程：

求解线性方程组即可得到a、b、σ的估计值

3 试验方案的优化设计

3.1 优化准则和目标

根据对试验结果的不同要求，加速寿命试验的优化设计主要有两类优化准则，即D 最优准则和V 最优准则。根据不同的优化准则，可以得到不同的优化计算结果。本文同时采用两种优化准则，避免单一优化准则的局限性，并通过两种优化准则的对比分析，验证试验方案优化设计的准确性。

3.1.1 D 最优准则

考虑模型参数估计精度的要求，一般以最小化模型参数的协方差阵的行列式为目标函数进行优化。协方差阵的行列式越小，参数估计精度就越高，即D 最优准则优准则下试验方案的最优解。

基于整体最佳线性无偏估计理论，模型参数的协方差阵为：

其中，

根据前面分析加速度计实际寿命服从威布尔分布，可以转化为I 型极小值分布，则μjk是第个j应力水平下，标准I 型极小值分布的第k个顺序统计量的均值，vjkl是第j个应力水平下，标准I 型极小值分布的第k个和第l个顺序统计量的协方差。

通过上述公式可以看出：最小化协方差阵的行列式可以等价为最小化矩阵CM的行列式，通过最小化CM行列式可以求得在D 最优准则下试验方案的最优解。

3.1.2 V 最优准则

考虑对产品寿命预测的精度要求，一般选取正常使用应力水平下的一个P 分位寿命的渐近方差为目标函数进行优化，即V 最优准则。最小化分位点寿命估计值的渐近方差，可求得V 最优准则下试验方案的最优解。

威布尔分布可以用线性—极值/正态模型来进行方差估计。对线性—极值/正态模型来讲，在转化应力x下，产品分位点寿命g P(x) 是参数γ0、γ1、σ的函数，zp是标准极值分布的P阶分位数，其估计值为：

渐进方差为：

那么，在正常工作应力x0下，P分位寿命的渐进方差为：

3.2 试验约束条件

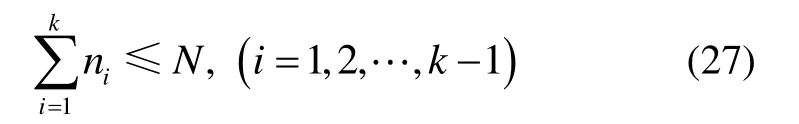
3.3 试验设计变量

优化设计变量为每个应力水平下分配的样本数。

在试验样本量的分配中，分配准则为：低应力下分配的样本数不应少于高应力下分配的样本数；同时，由于加速度计可靠性较高，试验时间不能过长。因此，对于恒加试验而言，需要综合考虑试验效率和试验精度对于试验的影响。

3.4 优化流程

1）开展加速度计的预实验，处理失效数据，确定加速度计的寿命分布模型；

2）确定加速度计恒加寿命试验的温度应力水平和试验样本总量；

3）按照样本分配原则，列出样本在不同温度应力水平下的所有分配方案；

4）利用不同温度应力水平下样本失效时间的顺序统计量，通过最佳线性无偏估计，估计不同分配方案下加速计的寿命分布模型参数；

5）求解模型参数协方差阵的行列式，找出其最小值所对应的样本分配方案；

6）求解0.5 分位点寿命的渐进方差，找出其最小值所对应的样本分配方案；

7）对比两类优化准则的求解结果，确定加速度计最终的加速寿命优化设计方案。

4 优化设计结果

对于可能进行的试验方案（8 个试验样品分配到三个应力水平下），分别计算得到V 最优和D 最优的求解结果，并以（8|5,2,1）为例说明计算过程。

4.1 最佳线性无偏估计

设在95℃、110℃、130℃下分别有5、2、1 个样本进行定数截尾试验，完全失效的失效时间分别为t11≤t12≤t13≤t14≤t15、t21≤t22、t31。

以应力水平S1(T1=95℃)情况下为例：

令y= lnt，极小值分布的5 个顺序统计量为y11≤y12≤y13≤y14≤y15。

由于y1i=μ+σy10i,(i= 1,2,3,4,5)，所以：

其中，ε1i服从均值0，标准差为σ的极小值分布EV( 0,σ) ,(i= 1,2,3,4,5)，在应力水平S2(T2=110℃)、S3(T3=130℃)下与以上内容相似。

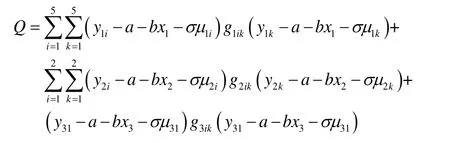
分别对a、b、σ求偏导，得到以下三个线性方程：

求解线性方程组即可得a、b、σ的估计值aˆ、bˆ、σˆ 。

4.2 优化准则和目标求解

4.2.1 D 最优准则

模型参数的协方差阵为：

其中，

例如：

其中，

4.2.2 V 最优准则

取0.5 分位点寿命，常温为25℃，即298K，h=(1 ,1/298,0)，那么，渐进方差为：

4.3 结 果

依照上述计算过程，分别计算得到各试验方案下V最优和D 最优的求解结果，如表2所示，其中：(n|n1,n2,n3)分别代表样本总数、应力水平S1下的样本数、应力水平S2下的样本数、应力水平S3下的样本数；σ= 1m，m是威布尔分布中的形状参数。

表2 优化计算结果 Tab.2 Optimized design results

在表2中，V 最优一列计算的是加速度计均值的渐近方差的估计值，根据V 最优准则，渐近方差越小，则表示试验的估计精度越高。D 最优一列计算的是矩阵CM的行列式的值，根据D 最优准则，行列式的值越小，试验的估计精度越高。由以上的计算结果对比分析可知，V 最优和D 最优这两种优化方法的求解结果一致，验证了加速度计恒加试验方案优化设计的准确性，确定加速度计的试验方案为（8|4,2,2），即在应力水平S1、S2、S3下分配的样本量分别为4、2、2。

5 结 论

1）将顺序统计量引入加速寿命试验优化设计中，运用整体最佳线性无偏估计理论，解决了模型参数先验信息未知情形下的优化设计问题。

2）与常用的极大似然估计法相比，基于顺序统计量和整体最佳线性无偏估计理论的参数估计方法，能够综合利用不同应力间的横向信息，提高参数的估计精度，在小样本情况下也具有良好的性质。

3）同时以加速度计在正常应力水平下中位寿命估计值的方差最小和模型参数的协方差阵行列式最小为优化目标，兼顾了模型参数估计精度和加速度计寿命预测精度，避免了单一优化目标的局限性。

4）根据顺序统计量和整体线性无偏估计理论，以每个应力水平下的样本分配为设计变量，同时以加速度计在正常应力水平下中位寿命估计值的方差最小和模型参数的协方差阵行列式最小为优化目标，建立加速度计定数截尾恒加寿命试验优化设计的数学模型。最后计算结果表明，两种优化目标的求解结果一致，确定加速度计的试验方案为（8|4,2,2），即在应力水平S1、S2、S3下分配的样本量分别为4、2、2，验证了该方法的可靠性。