多模式混合推进悬停控制与半物理仿真系统

任家栋，张大力，夏红伟，曾庆双

（哈尔滨工业大学 航天学院，哈尔滨 150001）

航天器相对运动控制在空间状态监测、组部件替换、燃料加注和对接等在轨服务任务中得到了大量应用。悬停是其中最为重要的相对运动构型，要求任务航天器相对目标航天器在空间某一固定区域内实现较长时间的逗留。比较典型的悬停区域为目标航天器的正上方（指天方向）或正下方（指地方向）[1]。

国内外对悬停控制进行了较多的研究，文献[2-4]等采用连续变推力的开环控制策略，研究了任务航天器任意位置悬停控制策略，该策略要求推力器提供特定加速度，对化学推进或电推进体制的发动机要求较高，工程应用难度较大。为此，一种“水滴”型悬停轨道引起了国内外学者的广泛关注。文献[5][6]分别基于CW 方程和相对轨道参数对“水滴”型形态进行描述，但相关运动参数较多，设计较为复杂。文献[7]对“水滴”型悬停形态的形成机理和存在合理性进行了分析，并设计了基于构型尺寸的四参数设计法，但上述方法选取的设计参数与构型设计的反演关系复杂，且仅适用于脉冲型控制策略。

近年来，电推进由于其高比冲、连续小推力特性成为目前航天领域研究的热点，包括地火转移[8-9]、轨道交会[10-11]、卫星编队[12-13]等，尤其在地球静止轨道卫星应用方面[14]。但全电推进难以同时满足轨道转移对快速性与燃耗效率的需求，因此多模式电推进与化学推进的优势组合得到广泛关注。文献[15]研究了GEO 转移轨道下混合推进的优化配置以及应用策略，得到最优的燃耗与时间的组合性能。文献[16]研究了不同质量约束下的电推进功率和推力幅值组合要求。文献[17]以入轨有效载荷质量转移率最优为目标，给出了一种解决多模式电推进和任务耦合优化问题的通用方法。电化混合推进体制以及多模式电推进在在轨服务等领域也存在较大的应用前景，如快速位置转移、高精度位置保持等，但相对而言，工程与理论问题的研究成果较少。

本文基于相对轨道参数的描述方法，采用半长轴差和偏心率差两个参数对面内“水滴”悬停构型进行深入研究，分析构型的形成条件；然后，给出悬停构型的参数描述和基于两轨道参数的构型设计方法，同时考虑多模式电推进与化学推进组合下构型的演化特性，给出混合推进体制下的面内悬停两参数设计方法；最后设计一套空间运动仿真验证系统，结合具体算例对不同构型参数下电化一体制导控制策略进行试验验证，进一步完善了“水滴”悬停制导的相关理论，同时也是对空间运动控制技术地面通用验证方法的有益探索。

1 混合推进悬停控制

1.1 相对运动建模

相对运动坐标系定义为目标航天器轨道系，原点O为目标航天器质心，坐标轴OX、OY、OZ分别沿目标航天器轨道迹向、轨道角动量反方向、径向。

采用轨道根数差对相对运动坐标系下任务航天器的位置矢量 [x y z]T进行描述[18]：

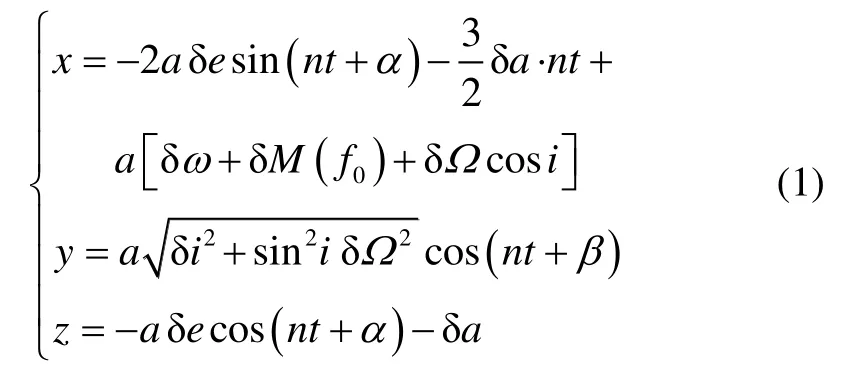
其中，

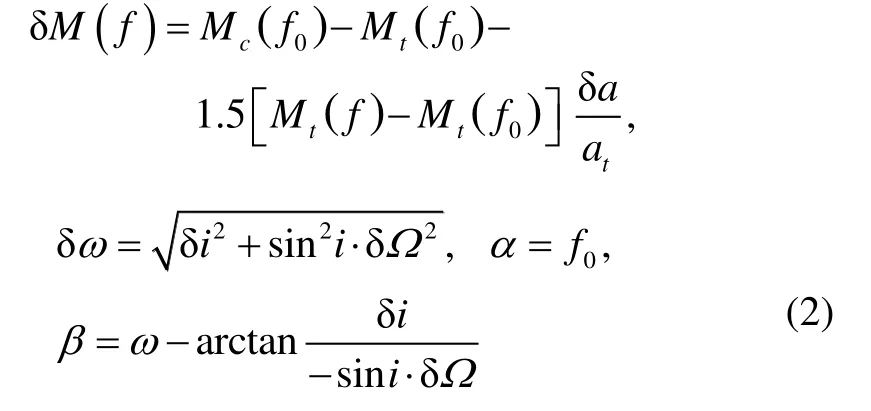
式中，[a,e,i,ω,Ω,f]为轨道六要素，分别为轨道半长轴、偏心率、轨道倾角、近地点幅角、升交点赤经和真近点角；n为轨道角速度；M为平近点角；下标c代表追踪星；下标t代表目标星；δ(* ) 为对应的轨道要素差。

两航天器相对运动的面内运动和面外运动解耦，不考虑编队构型的面外运动，a[δω+ δM(f0)+δΩcosi]项表示两航天器的迹向距离，不影响航天器构型，在构型分析过程中不予考虑。那么式(1)可进一步简化为：

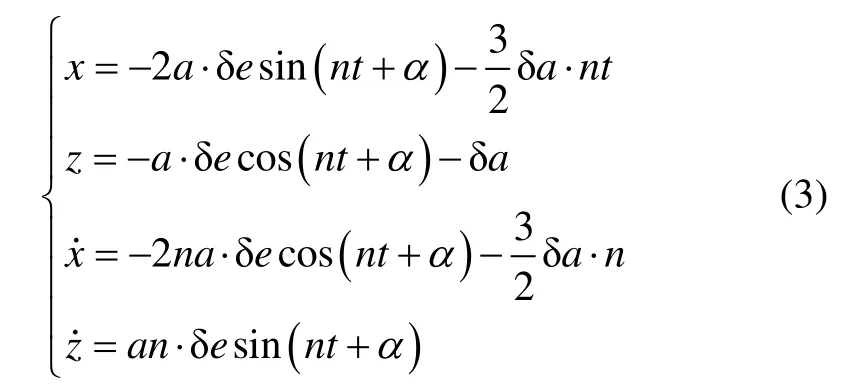
由式(3)可见，两航天器相对运动的面内构型在物理上由两航天器的半长轴差δa和偏心率差δe决定的，通过上述两参数的组合配置，可实现各类期望的面内构型。

1.2 脉冲推进悬停构型设计

水滴构型是一种特殊的相对运动面内构型，在两航天器自由漂飞状态下自然形成，具有一定的对称和闭合特性，适应于脉冲推进体制，实现特定频次的构型重访，可应用于悬停控制，具体如图1所示。

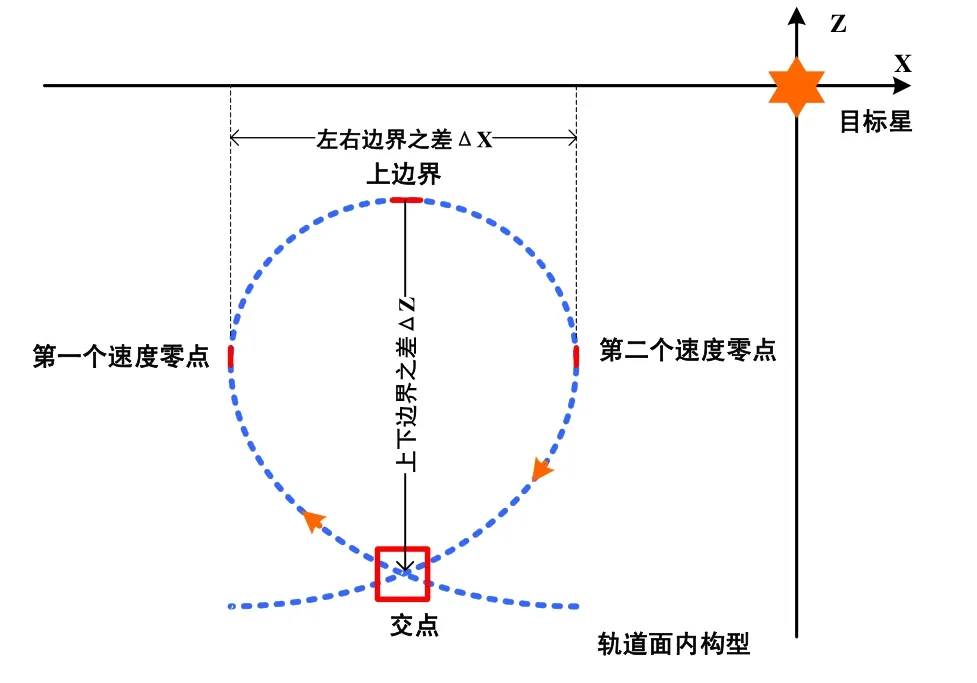
图1 水滴形轨迹的特征图 Fig.1 Characteristic map of the drop-shaped trajectory

根据构型的特征，定义如下参数对其进行描述：

构型的重访周期T：两次经过交点的时间间隔；

构型的上边界ztop：构型最高点的Z 向位置坐标；

构型的下边界zdown：构型交点的Z 向位置坐标；

构型横向尺寸Δx：构型的左右边界之差；

构型纵向尺寸Δz：构型的上下边界之差。

基于几何分析可得，悬停构型形成的充要条件为相对运动的X向的相对速度存在两个零点。由式(3)可得 -2na· δecos(nt+α) - 1 .5δa·n= 0，存在两个数值解的充要条件为aδe＞ 0.75δa，可进一步改写式(4)：

根据相对运动关系水滴顶点处相位满足 (nt+α) = π，得到构型的上边界表达式：

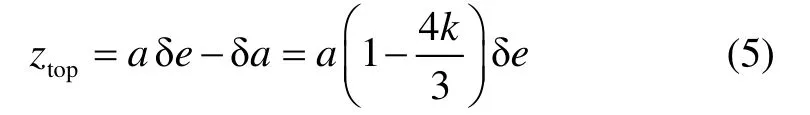
根据航天器两次经过交点时刻（一个重访周期）内，水滴关于交点与顶点连线左右对称，x方向速度积分和为0，即：

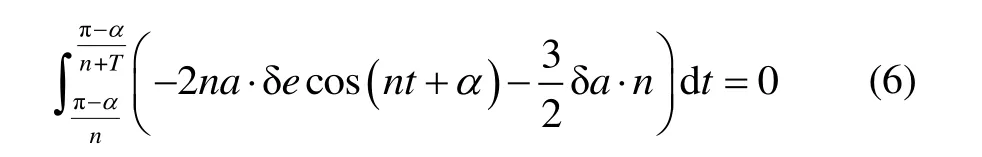
得到重访周期与两星半长轴以及偏心率之差的关系式如下：

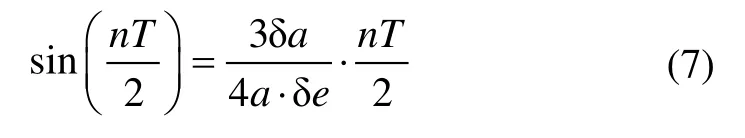
构型的下边界可式(3)从顶点位置运行nT/2，得到：

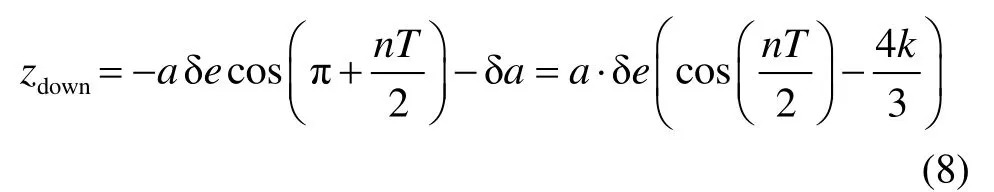
进一步得到构型的横向尺寸：

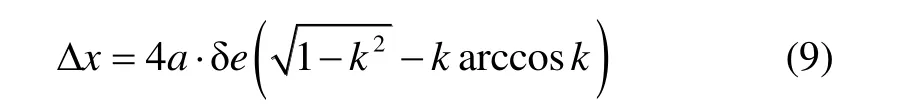
纵向尺寸：

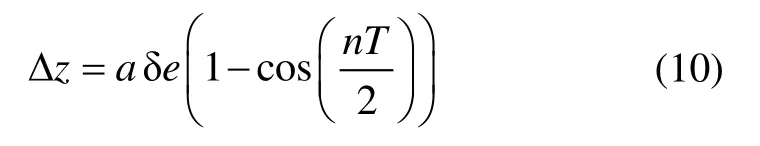
交点位置坐标：

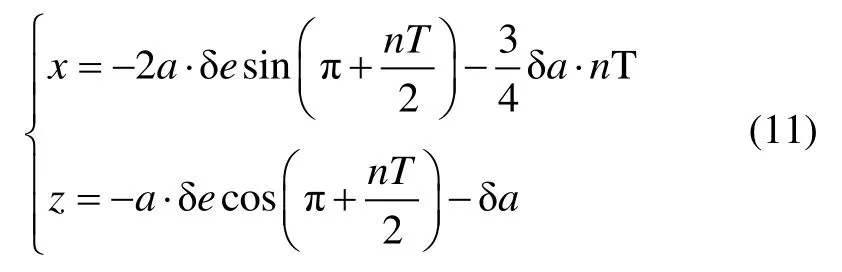
交点处改变Z向速度增量，可实现构型的重访，由于构型存在对称性，构型保持所需速度增量 Δvz是此刻Z向相对速度的2 倍，可表示为：

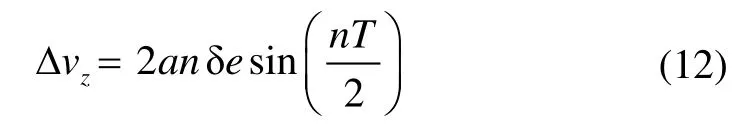
分析表明，在满足构型形成条件的前提下，通过调整两航天器的轨道高度和偏心率特性，可形成期望水滴型悬停构型。

1.3 混合推进悬停构型设计

混合推进的应用下，为了降低悬停期间的综合燃耗，电推进全程开机，但电推进的持续作用，使悬停构型与漂飞状态下的构型相比，对称性发生变化，无论从形态还是时间上，均不再具有对称关系，具体如图2所示。

电推进连续作用下的悬停构型，保持了原构型的主要特点，但由于电推进为非保守力作用，构型的对称性发生了变化。相对于构型交点所绘的构型中轴线，构型的左右边界不再相等，同时中轴线两侧的运行时间T1与T2也存在差异，这些均增加了制导设计的难度。电化一体悬停制导律设计的关键即为如何根据悬停位置和悬停时间要求，设计合理的悬停构型，并求解得到构型的重访时间T1和T2。

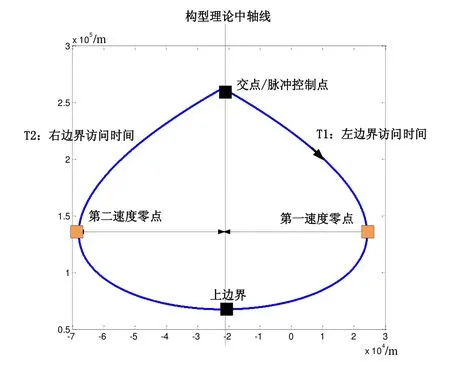
图2 电推进连续控制下悬停构型特性 Fig.2 Hovering configuration characteristics under continuous control of electric propulsion

在电推进的控制作用下，轨迹的异化特性可用图3表示。由图中可见，由于Z方向实施电推进的连续控制，造成了Z方向相对运行速度的近似线性偏移，相对于自由漂移状态，Z向速度的对称性破坏明显。由于轨道面内的相对运动存在耦合，Z向的构型异化必然导致X方向同步异化，异化轨迹呈现非线性特性。

虽然构型存在异化，但构型的闭合特性依然存在，在半长轴偏差量δa和偏心率变化量δe已知的情况下，满足：悬停构型稳定的控制策略为脉冲控制的开始时刻、喷气时长、喷气方向。取构型顶点时刻t0的相对位置、速度为X0=[x0y0z0vx0vy0vz0]T，并建立制导解算方程：

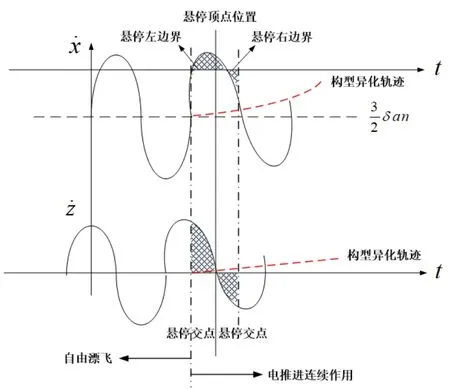
图3 电推进连续控制下轨迹异化机理 Fig.3 Trajectory dissimilation mechanism under continuous control of electric propulsion

其中，Φ x表示状态转移矩阵中的x相关行，Φ z表示状态转移矩阵中的z相关行；U1表示构型左半周期等效控制，U2表示构型右半周期等效控制；x(T1,U)和z(T2,U)表示电推进持续作用下的系统受迫运动特性。式(13)的一阶形式可表示为：

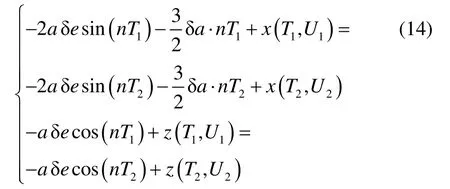
通过求解，得到构型左半周期时间T1、构型右半周期时间T2，以及保持所需速度增量 Δvz表达式：

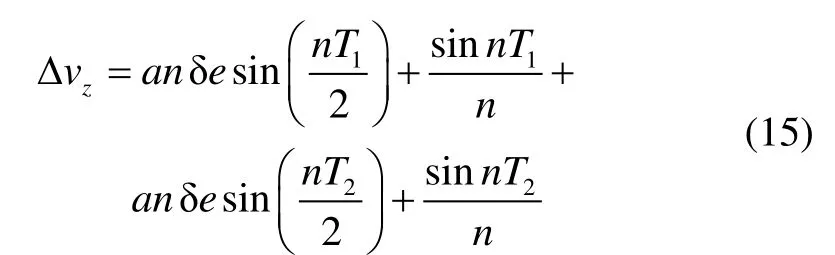
交点位置坐标为：

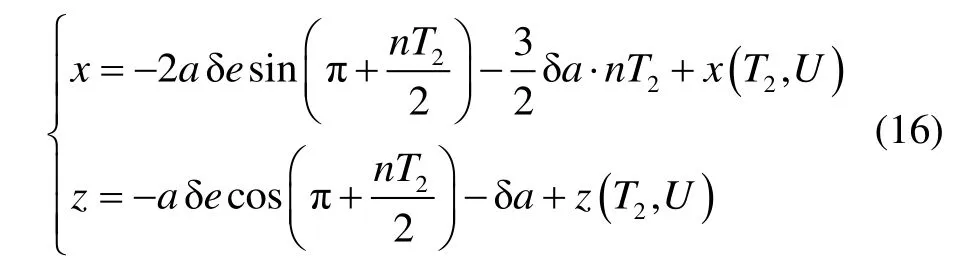
综合分析可得，混合推进悬停构型设计过程如下：

1）在构型的重访周期、上边界、下边界、横向尺寸、纵向尺寸等5 项构型参数中确定任意两个特征量，通过式(5)至式(10)中对应关系式建立两元方程组，求得该构型所需的两个设计参数：半长轴偏差量δa和偏心率偏差量δe。通常选择悬停的上/下边界和重访周期作为设计需求。

2）根据多模式电推进的使用需求，利用半长轴偏差量δa和偏心率变化量δe建立式(13)，求解得到电推进作用下构型的重访周期和上/下边界等构型特性。

3）如不满足设计需求，可采用一阶线性优化等方法修正第一步的设计输入，重复上述两个步骤，直至满足得到设计要求半长轴偏差量δa和偏心率变化量δe。

4）将第三步得到的设计参数根据式(15)得到化学推进的制导速度脉冲量，根据式(16)获取交点坐标，当构形经过该位置区域时进行制导控制，控制方向-Z，控制量 Δvz。

在实际的应用中，往往采用线性近似的方式进行悬停构型的设计，此时电化一体悬停的对称性依然存在，这是由于线性系统叠加原理的特性所带来的设计优势。但对于更为复杂的情况，如在悬停过程中要求在某个区间停止电推进工作（基于阴影区功耗等考虑，或者多模式电推进应用等），此时构型的对称性必然破坏，但式(13)依然满足此类需求和应用场景下的悬停设计要求。

2 半物理仿真试验系统

2.1 空间运动仿真总体方案

悬停控制的半物理仿真主要基于空间运动模拟系统和空间环境模拟系统组成的空间运动仿真系统开展。空间运动模拟系统采用大尺度、多维度、高精度的运动模拟系统实现，实现目标航天器和任务航天器位置、姿态共12 维度的运动模拟；空间环境模拟系统采用微波暗室及目标回波特性模拟等实现空间电磁环境以及目标电磁特性的模拟。试验系统结构关系如图4所示。

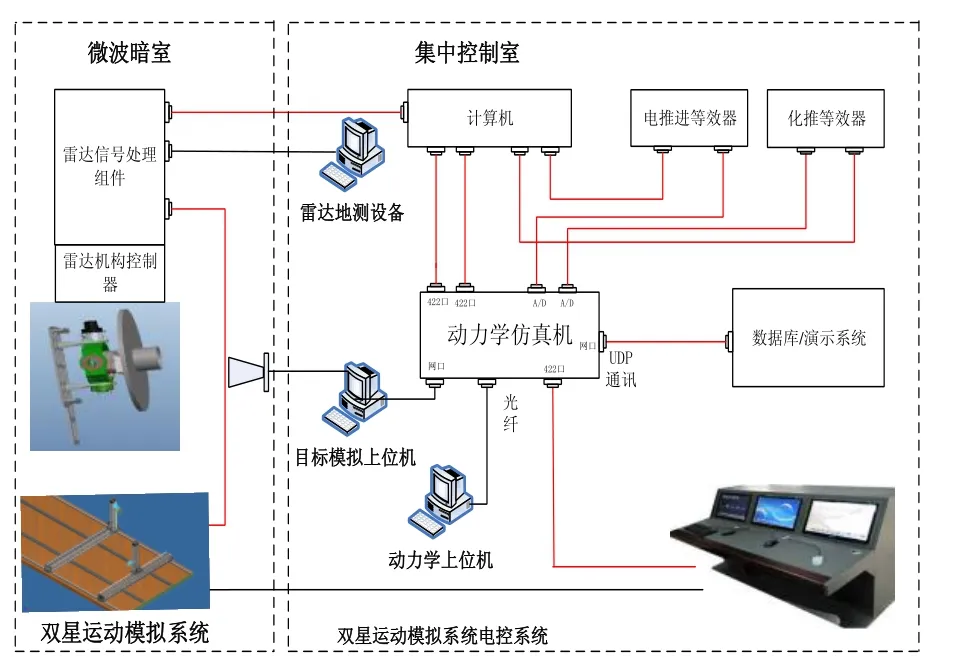
图4 电推进连续控制下轨迹异化机理 Fig.4 Structure diagram of space motion simulation system

图4中雷达及其目标模拟器安装于微波暗室内部，通过双星运动模拟系统实现两航天器空间运动关系的高精度模拟；微波暗室实现对空间环境的电磁环境模拟；目标模拟器上位机及双星运动模拟电控系统放置于集中控制室，实现对目标航天器的电磁回波特性模拟；集中控制室与微波暗室内通过光纤网络等高速局域网进行数据通信。动力学仿真实现两航天器在轨姿态/轨道动力学特性的仿真以及成熟单机如飞轮、陀螺等单机的数学模型仿真；计算机、推进等效器等实现对航天器在轨控制单元以及推进系统真实单机的特性模拟。

2.2 系统组成与工作原理

根据总体方案，半物理仿真试验系统主要由试验系统和航天器上单机/模拟系统组成。试验系统主要包括：微波暗室、动力学仿真机、双星运动模拟系统、 目标模拟器；星上单机/模拟系统包括：计算机、雷达模拟器、化推模拟器、电推模拟器。各模块的关键功能和性能配置如下：

1）动力学仿真机

动力学仿真机（dSPACE）运行卫星动力学，模拟卫星在轨动力学特性。动力学将相对角度、相对位置信息等通过异步422 串口发给双星运动模拟电控系统，将实时仿真出的两星相对距离、相对角度等信息通过异步422 串口分别发给目标模拟上位机，并在动力学仿真机上位机上利用dSPACE 控制软件实时计算和绘制指向控制角误差，保存试验结果。具体功能及接口设计如图5所示。

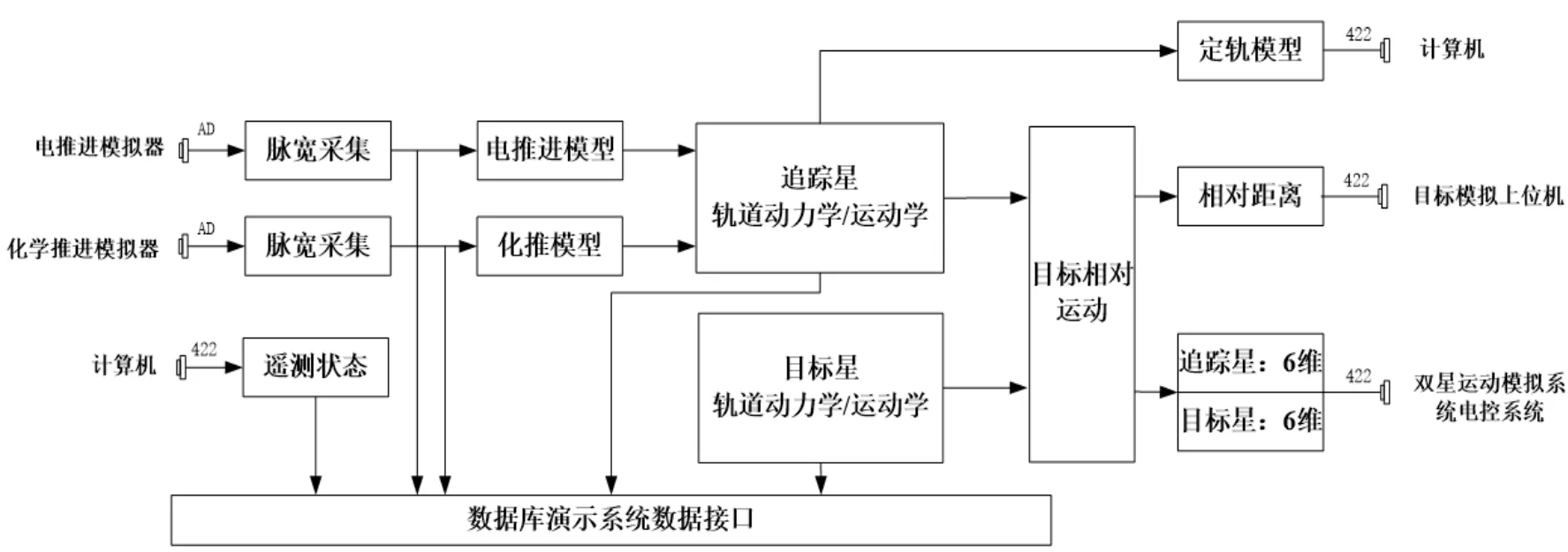
图5 动力学仿真模块组成 Fig.5 Composition of dynamic simulation module

2）双星运动模拟系统

双星运动模拟系统根据动力学相对信息同步控制追踪星和目标星运动模拟器平动及转动位置，缩比模拟两星的相对运动，并采集和存储双星三维平动位置传感器及三维转动角度传感器的测量信息。

该系统由“床身系统”、“目标星运动模拟系统”、“追踪星运动模拟系统”、“电控系统”以及“综合监控系统”五部分组成，如图6所示。

目标星运动模拟系统和追踪星运动模拟系统均为六自由度运动模拟器，用于模拟目标星和追踪星的三维平动和三维转动。平动部分由横梁和竖梁组成，转动部分由三轴转台组成。横梁沿床身的导轨移动，作为X方向运动；竖梁安装在横梁上，并沿着横梁上的导轨做Y向运动；三轴转台安装在竖梁上，并沿着竖梁上的导轨做Z向运动。X和Y向运动采用精密滚动导轨导向，齿轮齿条传动；Z向运动由于和重力方向重合，驱动形式需要能够克服重力作用，采用导轨和滚珠丝杠驱动形式，锁定采用伺服电机带的抱闸装置，在发生意外的情况下能够锁定系统，平动运动模拟可以实现30 m×15 m×5 m 的运动行程，位置精度达到毫米级。

3）敏感器和推进系统：

目标模拟器进行目标回波特性的模拟，包括RCS、多普勒等效应，主要由前端、调制器、喇叭天线等组成，实验室安装如图8所示。

雷达跟瞄配置微波雷达，采用驱动机构+脉冲测角体制进行目标跟踪捕获，主要指标包括：

视场范围：俯仰±30°，偏航±30°；

测距范围：>100 km；

测距精度：5 m（3σ）；

测角精度：0.05°（3σ）；

驱动机构测角分辨率：0.001°；

通信周期：5 Hz；

输入电压：DC 23～37 V。

推进系统包括化学推进和电推进两类，进行脉宽模拟，共16 套。

化学推进，由12 套喷气电磁阀构成（+X、-X、-Y、+Y、+Z、-Z等六方向各2 套），主要技术指标：

1）额定推力：10 N；

2）最小脉宽：7 ms；

3）电磁阀开/关时间：10 ms/15 ms；

4）比冲：285 s。

电推进由4 套喷气电磁阀构成（+Z、-Z方向各2套），主要技术指标：

1）额定推力：80 mN 或160 mN；

2）最小脉宽：7 ms；

3）电磁阀开/关时间：10 ms/15 ms；

4）比冲：1600 s。

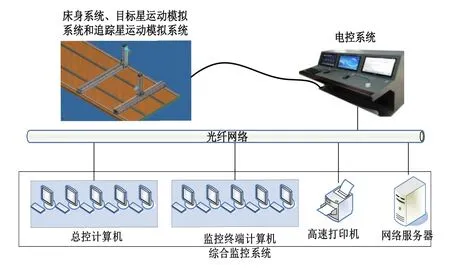
图6 双星运动模拟系统组成 Fig.6 Composition of two-satellite motion simulation system

图7 目标星运动模拟系统和追踪星运动模拟系统 Fig.7 Target and tracking satellites motion simulation system

图8 试验环境中目标模拟器（左）和雷达跟瞄（右） Fig.8 Target simulator (left) and radar tracking (right) in test environment

4）计算机

计算机运行卫星应用软件，根据接收到的雷达测量信息，通过控制律解算，发送推力器控制指令，调整两星相对位置关系。

2.3 半物理仿真系统仿真流程

仿真系统的具体工作流程主要包括以下步骤：

1）设置两星初始轨道位置，运行动力学仿真机，模拟卫星轨道动力学特性。动力学仿真机将相对角度、相对位置等信息发给双星运动模拟电控系统，将实时仿真出的两星相对距离、相对角度等信息发给目标模拟上位机。

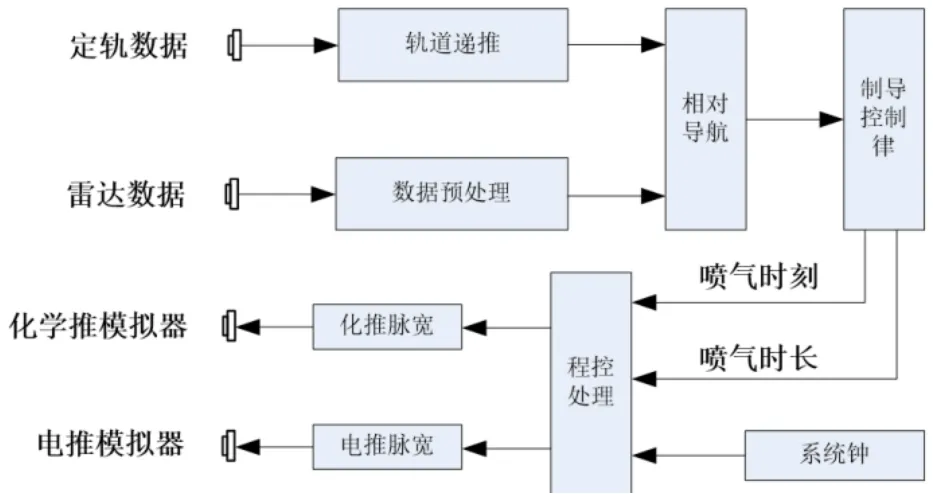
图9 计算机功能模块组成 Fig.9 Composition of computer function module

2）双星运动模拟系统根据相对位置信息同步控制追踪星和目标星运动模拟器平动及转动位置，缩比模拟两星在轨的相对运动状态，并采集和存储双星三维平动位置传感器及三维转动角度传感器的测量信息。

3）目标模拟器上位机收到动力学数据后，采集雷达的射频信号进行延时、调制后将目标回波信号由雷达目标模拟器极化后射出，雷达接收到目标模拟器的回波信号，完成目标捕获并跟踪，同步输出相对距离、相对俯仰角和相对方位角，并将测量信息通过异步422 发送到计算机。

4）计算机根据接收到的雷达测量信息，通过控制律解算，发送推力器脉宽指令；动力学仿真机采集脉宽开关状态，产生相应作用力反馈至轨道动力学。

3 仿真验证

针对典型的空间悬停任务（如正下方50 km，悬停时长10 h），采用本文提出的混合推进悬停构型设计方法，在半物理仿真实验系统中进行试验验证，分析其构型稳定精度。

航天器平台配置4 台80 mN 电推进，12 台10 N推力器发动机，悬停过程中由于功耗等限制，电推进采用多模式工作方式，构型左边界期间4 台电推进全开，构型右边界期间仅开启2 台电推进，根据任务要求要求，采用2.3 节的设计步骤，得：构型上边界ztop为50 km；构型左边界时间T1为4665 s；构型右边界时间T2为4364 s；交点处的控制脉冲量 Δvz为-6.02 m/s；

化学推进提供有限推力，控制时长在理论脉冲控制点前后进行平均分配，以抑制弧段损失。记录航天器运行至构型上边界时刻Time_up，得化学推力器启动区间为：

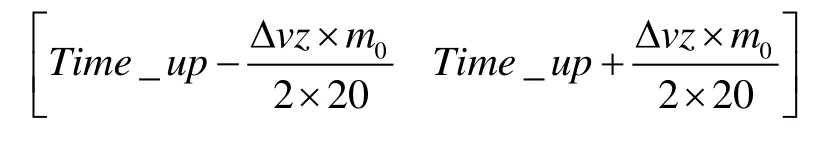
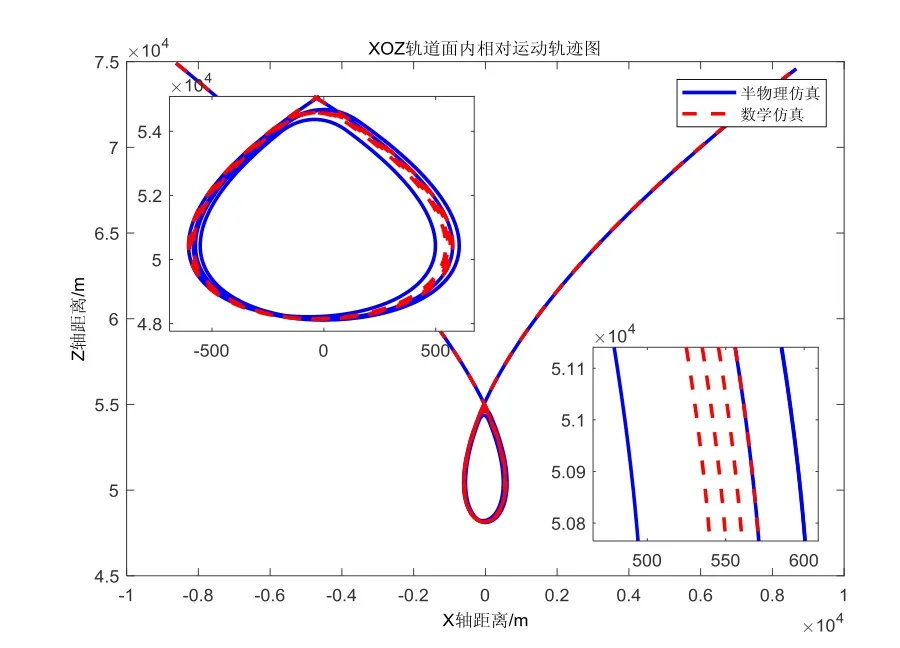
图10 电化一体悬停过程相对运动轨迹 Fig.10 Relative motion trajectory of electrochemical integrated suspension process

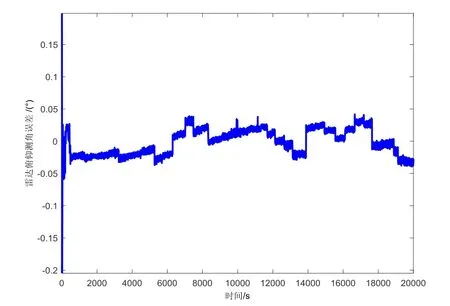
图12 半物理试验雷达俯仰角误差 Fig.12 Pitch angle error of radar in semi-physical test

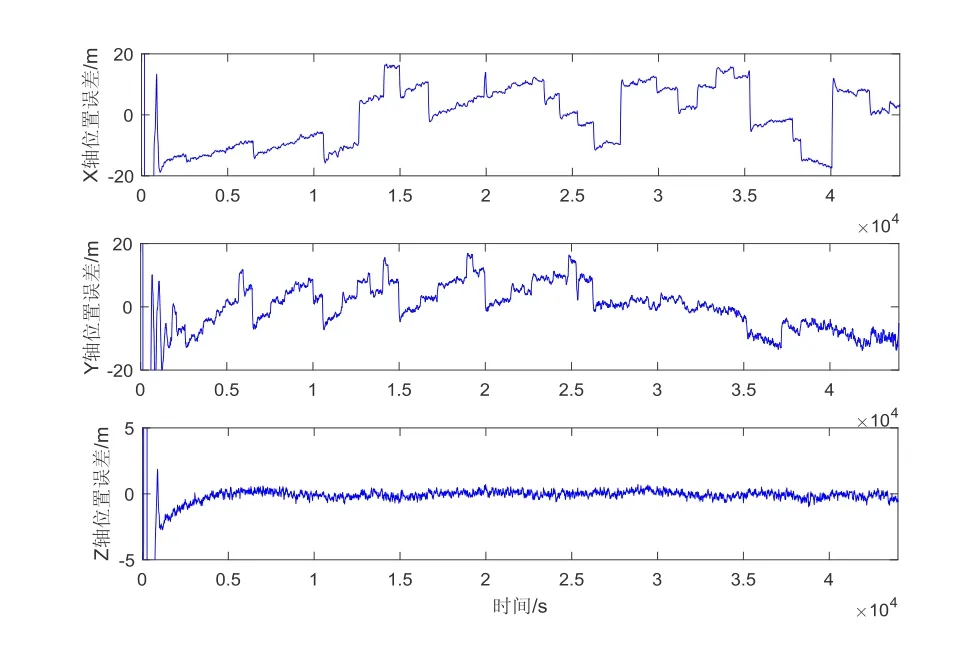
图14 半物理过程位置估计误差 Fig.14 Position estimation error of semi-physical process

半物理仿真试验系统的配置见第2 节，包括雷达模拟器、推进模拟器、计算机等。航天器质量1800 kg， 控制周期0.5 s，实现在目标航天器下方50 km 附近的10 h 左右的悬停，同样条件下的数学仿真和半物理仿真验证情况见图10～15。

仿真表明，制导控制律设计正确。数学仿真情况下受限于有限推力等因素构型漂移约10 m/周期；半物理仿真下构型漂移较大，且不均匀，最大漂移达80 m/周期；实际半物理仿真中由于推力器模拟器的误差、控制回路的误差、雷达测量的误差等致使控制策 略的误差变大。相对而言，半物理试验的导航估计误差较大，且分布特性复杂，位置估计误差20 m (3σ)左右，速度估计误差0.1 m/s (3σ)左右，致使控制策略与数学仿真在控制的时刻以及控制量上均存在偏差，构型稳定性能较数学仿真略差。

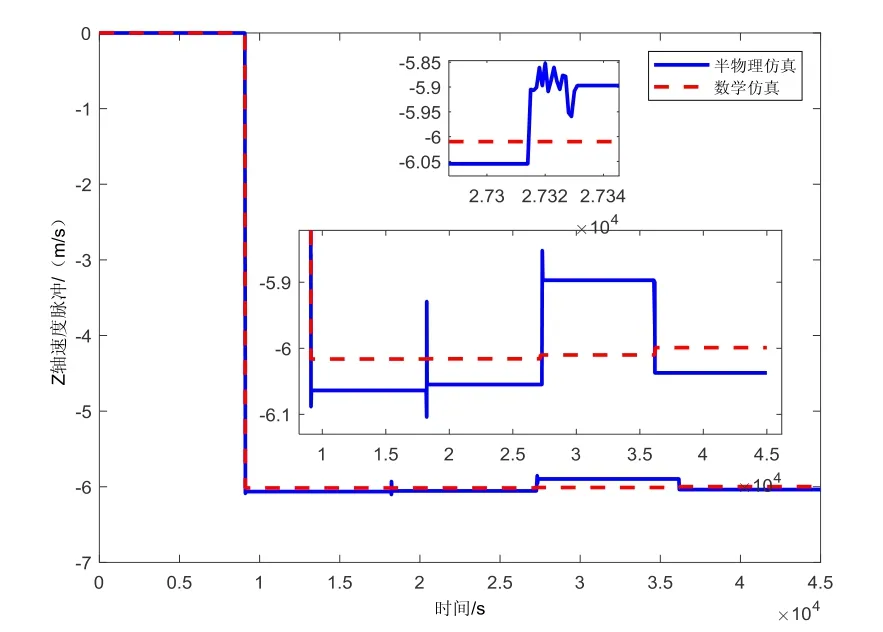
图11 数学仿真和半物理仿真Z 轴速度脉冲曲线 Fig.11 Mathematical simulation and semi-physical simulation of Z-axis velocity pulse curve

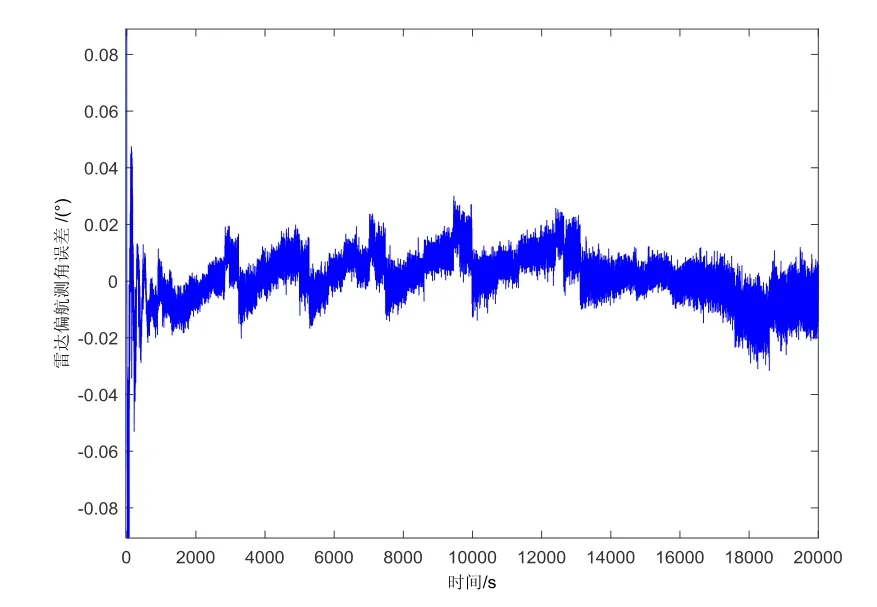
图13 半物理试验雷达偏航角误差 Fig.13 Yaw angle error of radar in semi-physical test

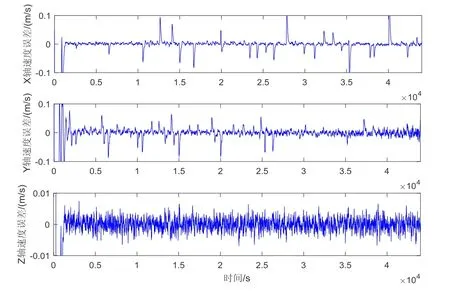
图15 半物理过程速度估计误差 Fig.15 Velocity estimation error of semi-physical process

4 结 论

本文采用相对轨道参数的描述方法，采用半长轴差和偏心率差两个参数对面内“水滴”悬停构型的形成进行了深入研究，得到了构型的形成条件；推导了基于半长轴差和偏心率差两参数的水滴悬停构型设计方法，同时分析电化一体推进体制下构型的演化特性，提出了一种多模式混合推进体制下的面内悬停两参数设计方法和制导方案；设计了一套空间运动仿真试验系统对本文提出的悬停控制技术进行半物理验证，试验表明，制导方案正确有效，同时试验系统和验证方法具有通用性，可推广应用于其它相对运动控制技术的地面验证。