陀螺电机用H型动压气体轴承启动摩擦特性分析
2019-11-20任天明忽敏学刘志宏
任天明,冯 明,忽敏学,刘志宏
(1.北京科技大学 机械工程学院,北京 100083;2.天津航海仪器研究所,天津 300131)
H 型动压气体轴承具有动量矩指向精度高、噪声低和可靠性好等优点[1-3],是陀螺电机的主要支撑方式之一。但其基于气膜动压效应的工作原理决定了在启动和低转速时转子与轴必然会发生接触与摩擦,导致轴的磨损,甚至表面微粒的脱落,严重时造成气体轴承无法启动,降低陀螺电机的可靠性和寿命。
针对陀螺电机中动压气体轴承的启动特性,王京峰[4]等讨论了安装姿态对轴承静摩擦力据和转子浮起时间的影响,指出倾斜安装时气体轴承的静摩擦力矩更大,需要的浮起时间也更长,但其假设轴承启动时摩擦系数为常数,并未考虑表面粗糙度的影响。Cui[5]和Zhang[6]等分别对考虑表面粗糙度影响的径向和止推轴承的启停特性进行了分析,结果显示表面粗糙度对轴承运动、浮起转速、最大接触压力等特性有显著的影响。Henry[7]和Braun[8]等在对粗糙表面形貌特征的研究中发现,适当的微观形貌可减小粗糙表面的摩擦系数、提高轴承的承载力。
本文采用 Kougut[9]等提出的粗糙接触模型及Pair[10]等提出的平均流润滑模型,建立可考虑表面粗糙接触与润滑的H 型动压气体轴承模型,对轴承启动过程中的粗糙接触和摩擦问题进行研究,并分析表面粗糙度和腔型结构参数的影响,为陀螺电机用气体轴承启动特性研究和结构设计提供理论依据。
1 H 型动压气体轴承分析模型
图1为水平安装的H 型动压气体轴承的结构示意图,该轴承由带有螺旋腔的径向轴承和止推轴承组成。在轴承启动前,转子处于重力和径向轴承接触承载力相平衡的静止状态。启动过程中,转子与径向轴承之间存在接触和摩擦,且随着转速的升高,径向轴承气膜承载力增大,使转子与轴逐渐脱离接触。为对H 型动压气体轴承的启动特性进行研究,需建立同时考虑轴承运动、轴承表面粗糙接触和润滑的分析模型。
1.1 轴承运动方程
在H 型动压气体轴承的质心建立o-xyz坐标系(如图1所示),轴承转子在该坐标系内的五自由度运动方程为:

式中,m为转子质量,eu为转子质量偏心,Ii(i=x、y、z)为转子绕各个坐标轴的转动惯量,Ω为轴承转速,g为重力加速度,θ为转子绕z轴的转角,φx和φy分别为转子绕x、y轴的转角,Fi(i=x,y,z)为轴承的反作用力,Mi(i=x,y)为轴承绕坐标轴的反力矩。
轴承由静止状态启动,假设在驱动力作用下其转速曲线为正弦形式:

其中,Ωn为启动目标转速,Tn为启动时间。
1.2 轴承表面粗糙接触和润滑模型
对于采用水平安装的H 型动压气体轴承,启动过程中的粗糙接触与摩擦仅发生在径向轴承,根据轴承内气膜厚度的大小,将其润滑分为全膜润滑和粗糙接触与润滑两部分。而止推轴承中因不发生接触,其润滑为全膜润滑。

图1 H 型动压气体轴承结构示意图 Fig.1 Schematic of H-type hydrodynamic gas bearing
1.2.1 全气膜润滑
在全气膜润滑区域,气膜厚度较大,可通过雷诺方程的求解得到气膜压力。径向、止推轴承的气体润滑雷诺方程分别为:

其中,μ为气体粘度,pjh、pt分别为径向和止推轴承内气膜压力,hj、ht分别为径向、止推轴承的气膜厚度,
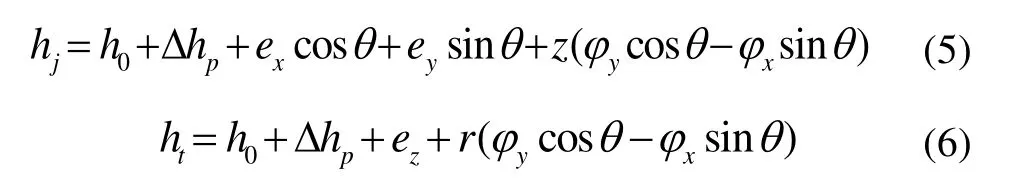
其中:h0为轴承设计间隙;hp为腔深,在有腔区域内Δ=1,反之Δ=0;ex、ey、ez分别为轴承沿各个方向的偏心。
对H 型轴承,径向、止推轴承在交界处应满足压力相等、流量相等的边界条件: 径向、止推轴承的气膜的剪切力为:

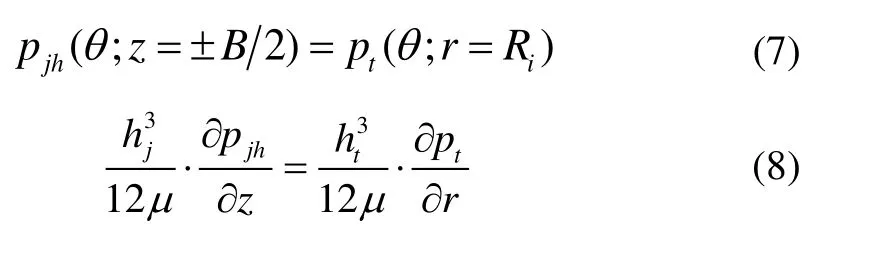
1.2.2 粗糙接触与润滑
在粗糙接触与润滑区,转子与轴发生粗糙接触。这里将两个粗糙表面当量为一个复合粗糙表面(轴)和一个光滑表面(转子),并假设复合粗糙表面覆盖有随机分布的粗糙峰,粗糙峰峰顶高度的概率密度函数为ΨS(δ),标准差为σS,峰顶面密度和峰顶半径分别为NS和RS。轴承粗糙接触与润滑模型如图2所示:h为粗糙表面高度均面到光滑表面的距离,即轴承的名义间隙;d为粗糙峰峰顶高度均面到光滑表面的距离;hT为局部间隙,即两粗糙表面的实际间隙;δ为粗糙峰峰顶的高度。
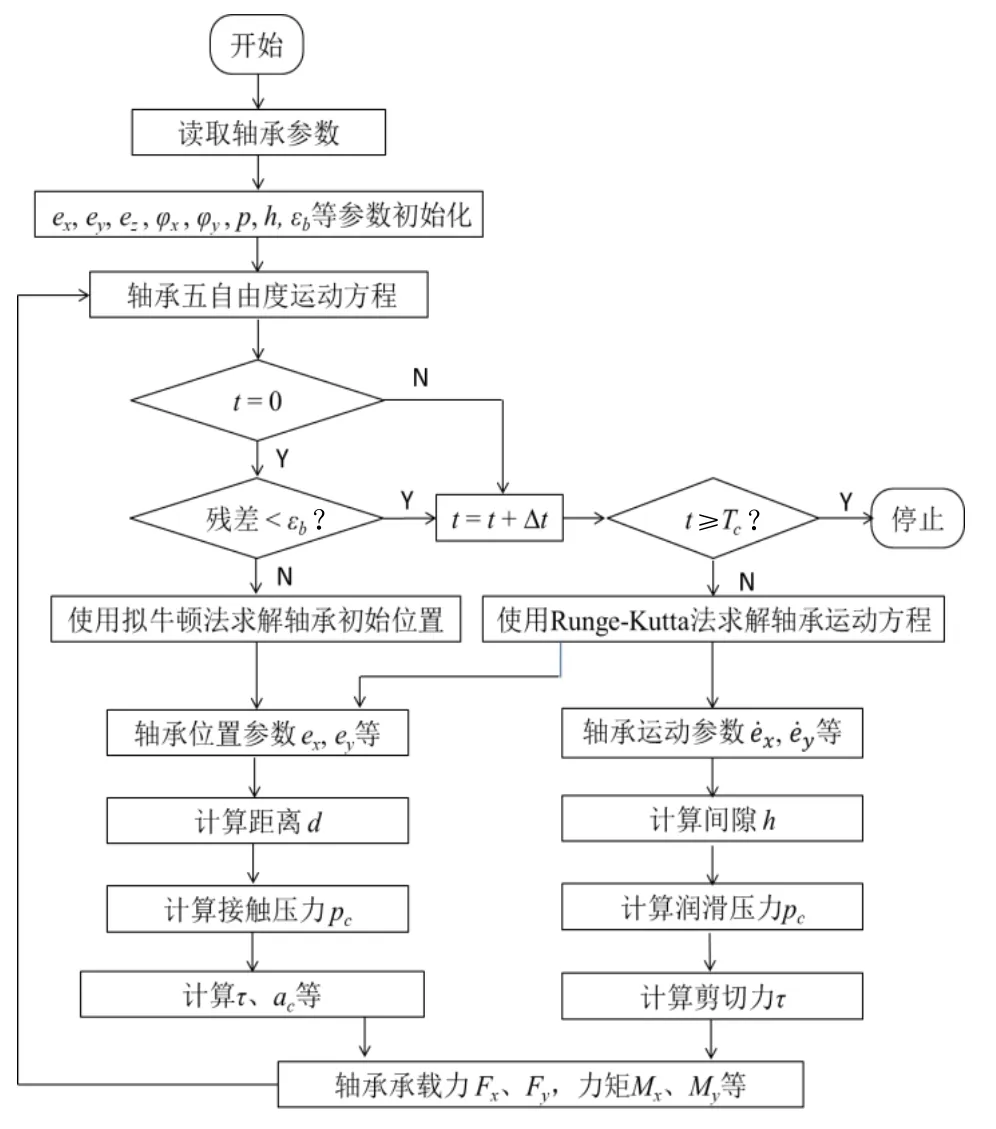
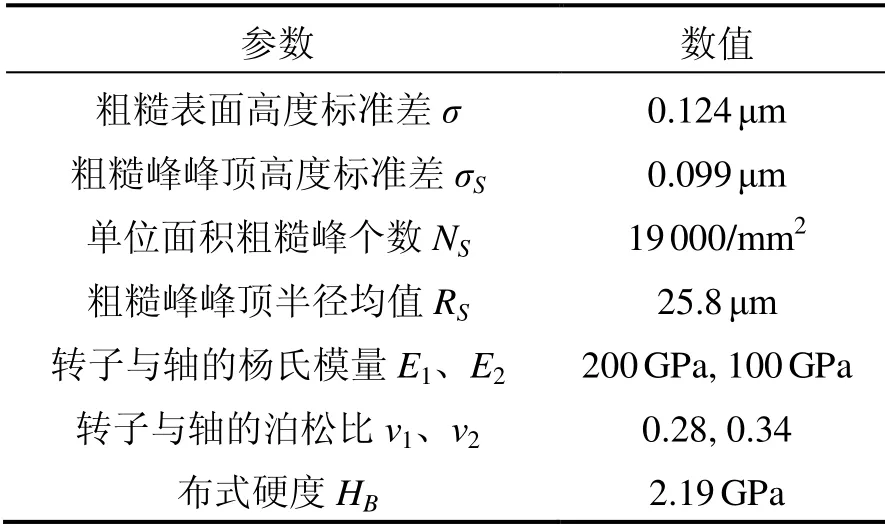
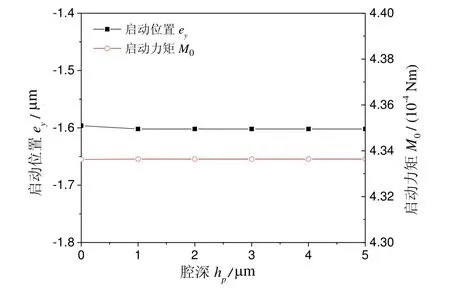
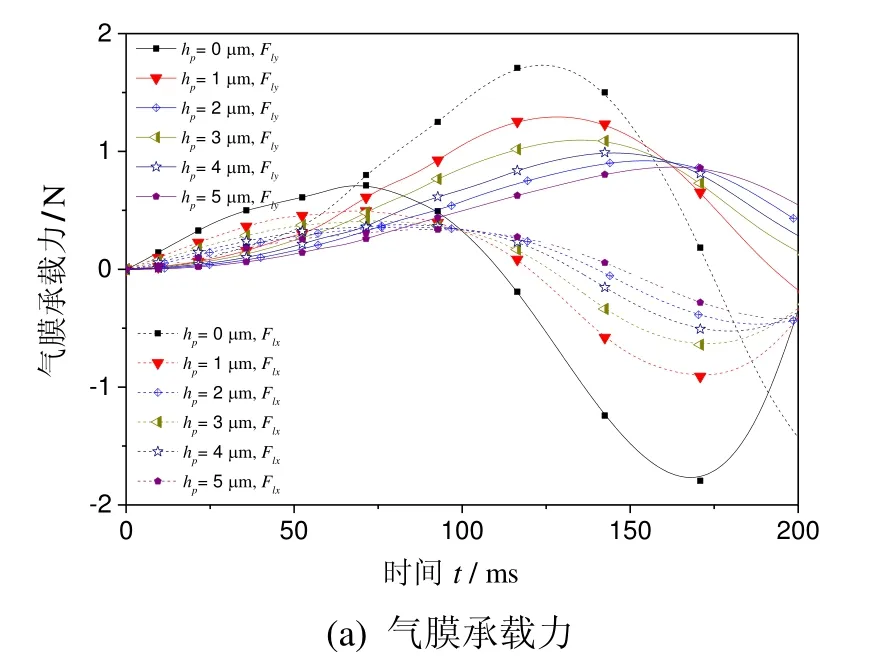
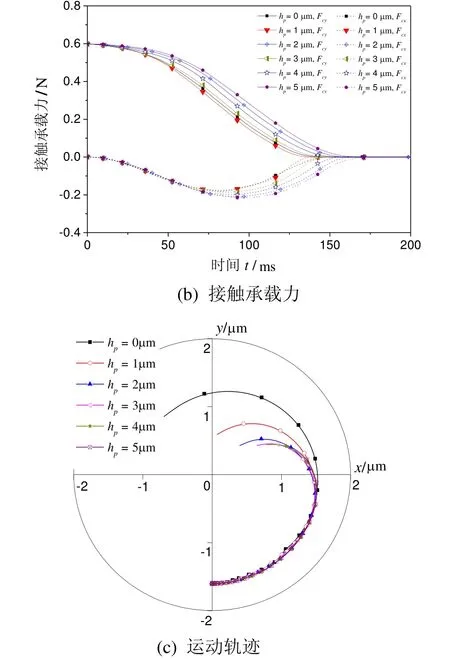
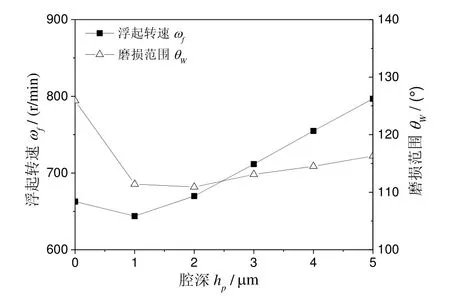
根据粗糙峰峰顶高度δ的大小,粗糙接触与润滑区进一步分成黏着区(δ≥d)和部分膜润滑区(δ 1)黏着区 当δ≥d时,粗糙峰与光滑表面发生接触。假设仅粗糙峰的峰顶发生弹塑性变形,而忽略粗糙表面的基体变形,粗糙接触压力pc为[9]: 其中:W(d)中的四个积分项及其上下限分别表示粗糙峰在完全弹性变形区、弹塑性变形区和完全塑性变形区的分布;ω=δ-d为峰顶的屈服值;ωp是单个峰顶由完全弹性变形转变为弹塑性变形的临界值, HB是转子与轴中硬度较低材料的布式硬度;K是与较软材料的泊松比有关的硬度系数,K=0.454+0.41ν6;E是复合表面的杨氏模量,定义为 其中,E1、E2和ν1、ν2分别是转子与轴的杨氏模量和泊松比。 两表面间弹塑性粗糙接触的剪切力为: 两表面间粗糙接触的真实接触面积为: 2)部分膜润滑区 当δ 其中,φpθ和φpz分别为考虑表面粗糙度影响的圆周和轴向的修正因子[10],为简化分析,不考虑表面粗糙度的各向异性,则有: 其中,H=h/σ;E(hT)是局部间隙的期望值[11], 其中,ψ(δ)是复合粗糙表面的概率密度函数。 部分润滑区内气膜剪切力为: 其中,φf和φfp是剪切流和压差流的修正系数, 通过雷诺方程及粗糙接触压力的求解,可得到轴承内压力分布及轴承承载力。径向轴承沿x、y方向的接触承载力为: 径向轴承沿x、y方向的气膜承载力为: 止推轴承的承载力及绕x、y轴的反力矩为: 轴承启动过程中的阻力矩为: 图3为H 型动压气体轴承启动特性计算流程图。计算时,首先确定轴承静止时的初始位置,求解轴承的粗糙接触压力,并采用拟牛顿法进行对轴承位置进行迭代修正,直至粗糙接触承载力与重力相平衡。然后对轴承的启动过程进行仿真计算,同时求解轴承的运动方程、润滑方程和粗糙接触方程等,并采用Runge-Kutta 法对轴承的运动轨迹进行迭代计算,得到轴承在启动过程中的位置、速度、承载力、阻力矩和接触面积等特性。当t>Tc,即完成设定的仿真时间时停止计算。 图3 H 型动压气体轴承起动特性计算流程图 Fig.3 Flow chart for numerical calculation of start-up characteristics of H-type bearing 轴承启动过程的仿真计算需要多步迭代,且为提高仿真精度,收敛精度和迭代时间步长都不能太大,因此所需总计算时间较长。在本文分析中,轴承启动目标转速为Ωn=3000 r/min,启动时间Tn=1.0 s,收敛精度εb=1×10-6,迭代时间步长Δt=2×10-6s。 H 型动压气体轴承几何参数和复合表面粗糙度参数分别如表1和表2所示[11]。 表1 H 型动压气体轴承参数 Tab.1 Parameters of H-type hydrodynamic gas bearing 表2 轴承复合表面粗糙度参数 Tab.2 Roughness parameters of bearing's composite surface 设定仿真时间Tc=Tn,对H 型动压气体轴承的启动过程进行仿真分析,得到从静止到目标转速的完整启动过程中轴承特性的变化,如图4~6 所示。 H 型动压气体轴承启动前处于静止状态,转子所受重力与接触承载力相平衡。轴承的静平衡位置位于-y轴方向,ey= -1.602 μm,此时轴承的真实接触面积ac为1.366×10-4mm2。图4为轴承接触压力分布云图,由图可见,转子与轴的粗糙接触主要发生在250°~290°的角度范围内的无腔区域,且在θ=270°,即-y轴的方向,有最大接触压力8209 Pa。 图4 H 型动压气体轴承启动前接触压力分布 Fig.4 Distribution of bearing contact pressure before startup 图5为H 型动压气体轴承的启动过程中承载力和运动轨迹随时间的变化。初始时刻,轴只有垂直方向的接触承载力Fcy=0.60 N,其大小与转子所受重力相等。轴承启动后,随着转速的升高,气膜承载力Flx和Fly逐渐增大,使得转子与轴脱离接触,接触承载力逐渐减小,直至轴承浮起,如图5(a)所示。在转子浮起前,其运动以沿轴表面的滑行为主。转子浮起后, 其运动轨迹随着转速的继续升高收敛到目标转速下的动态平衡位置(如图5(b)所示),气膜承载力在转速和转子偏心位置的影响下呈现出波动,并最终达到动平衡状态。在动态平衡位置,气膜承载力为Flx= 0,Fly=0.60 N,同样与转子重力相平衡。 图5 H 型动压气体轴承启动过程中承载力及运动轨迹 Fig.5 Variation of load capacity and trajectory of H-type bearing during start-up 图6为轴承启动过程中接触面积和阻力矩随时间的变化,由图可见,随着时间的增加,轴承接触面积先略有增大,然后减小。当t=161.9 ms 时,接触面积ac减至0,由式(2)计算可得轴承浮起转速Ωf= 754.9 r/min。此外,初始时刻的轴承阻力矩,即轴承的启动力矩为M0=4.337×10-4Nm。在轴承启动过程中,阻力矩呈现出先减小后缓慢增大的变化趋势。这主要是因为在转子浮起前,其阻力以轴承表面的粗糙接触剪切力为主,其随着接触面积减小而减小,气膜剪切力虽随着转速的升高而增大,但其数值较小,影响不大。而转子浮起后,粗糙接触剪切力消失,气膜剪切力随着转速的升高继续增大,导致轴承阻力矩增大。由于启动目标转速较低,气膜剪切力增大的趋势较为缓慢。 为分析轴承在启动过程中的摩擦磨损,以转子从启动到浮起所旋转的角度θf做为评价指标,如图5(b)中所示,θf越大,表明磨损范围越大。 受美国退出伊核协议及重启制裁的影响,伊朗的油气投资及石油出口目前几近陷入停滞,给已建项目投资回收带来较大压力,新进入项目的履约也面临挑战。中国石油企业应依托政府的力量,做好与资源国政府的沟通,协商解决目前面临的困难,并利用一切时机,加快提油和回收投资,降低风险损失,暂时不宜签署新的油气合同。 图6 轴承接触面积和阻力矩随时间的变化 Fig.6 Bearing contact area and reaction moment versus time 为验证理论分析的正确性,搭建实验平台对表1所给的H 型气体动压轴承的启动特性进行实验研究。由于轴承摩擦和磨损量很小,很难测量,因而仅对轴承的启动力矩和浮起转速进行验证。轴承启动力矩可由反力矩测试仪直接测得,而浮起转速很难直接测得,本文采用电阻法进行间接测量,如图7所示。当转子与轴接触时,两者间的电阻值为有限值,而浮起后电阻值会突然变大,因此转子与轴之间电阻突然增大时的转速即为浮起转速。 对轴承启动力矩和浮起转速分别进行了多次实验,结果如表3所示。实验所得启动力矩均值为4.49×10-4Nm,与计算值相差3.7%,而浮起转速均值为717 r/min,比计算值低5.0%。可见理论计算值与实验值相差不大,验证了本文理论模型与计算结果的正确性。 图7 H 型动压气体轴承启动特性实验台 Fig.7 Test rig of H-type hydrodynamic gas bearing 表3 H 型动压气体轴承启动力矩及浮起转速实验值 Tab.3 Experimental and theoritical results of startup characteristics of H-type hydrodynamic gas bearing 图8 轴承启动位置及启动力矩随峰顶标准差σS的变化 Fig.8 Bearing starting position and starting torque versus standard deviation of summit heights 图8为轴承启动前特性随粗糙表面峰顶标准差σS的变化。随着峰顶标准差的增大,轴表面粗糙峰的高度增大,转子与轴发生粗糙接触的偏心减小,因而静 平衡位置沿y轴正向移动。此外,由式(17)可知,粗糙峰弹塑性接触的剪切力也随着峰顶标准差的增大而增大,因而启动力矩增大,但增大的幅值较小。 图9为峰顶标准差不同时轴承启动过程中承载力和运动轨迹的变化。计算中,仿真时间Tc为0.2 s。由图9可见,不同峰顶标准差条件下轴承承载力的变化趋势相同。随着时间的增加,气膜承载力先增大后减小,在启动过程中有最大值。而随着峰顶标准差的增大,气膜承载力的最大值降低,且最大承载力出现所用时间增加,如图9(a)所示。结果表明气膜动压效应随峰顶标准差的增大而减弱,这也使得轴承粗糙接触的时间随着峰顶标准差的增大而延长,且接触承载力的下降趋势变缓,如图9(b)所示。图9(c)为轴承启动过程中的 运动轨迹。由于表面粗糙峰高度随着峰顶标准差的增大而增大,因此轴承的运动范围随着峰顶标准差减小。 图9 不同峰顶标准差条件下轴承承载力和运动轨迹的变化 Fig.9 Variations of bearing load capacity and trajectory under different standard deviations of summit heights 图10 为轴承浮起转速与磨损范围随峰顶标准差的变化,由图10 可见,随着峰顶标准差由0.05 μm 增大至0.15 μm,轴承浮起转速由644.3 r/min 增加至863.9 r/min,而磨损范围由76°增加至86°。 图10 轴承浮起转速与磨损范围随峰顶标准差的变化 Fig.10 Lift-up speed and wear zone of bearing versus standard deviation of summit height 由以上结果可知,随着峰顶标准差的增大,轴承浮起转速明显增大,启动力矩和磨损范围增加有限。为提高轴承的启动特性,可减小轴承表面峰顶标准差。 图11 为轴承启动位置和启动力矩随腔宽比的变化,由图可见,腔宽比对轴承启动位置和启动力矩影响不大。这主要是因为轴承表面粗糙峰峰顶高度随机分布,转子与轴在启动前的粗糙接触为有限个较高粗糙峰的接触,接触压力和剪切力的大小取决于表面粗糙度形貌参数和轴承载荷,而与轴承腔宽等结构参数关系不大。 图11 轴承启动位置和启动力矩随腔宽比的变化 Fig.11 Bearing starting position and starting torque versus groove width ratio 图12 为不同腔宽比条件下轴承启动过程中承载力和运动轨迹的变化。由图12(a)可见,随着腔宽比的增大,气膜承载力的最大值降低,且最大承载力出现所用时间增加。同时,轴承接触承载力减小为0 的时间也随着腔宽比的增大而增加,如图12(b)所示。结果表明,启动过程中气膜动压效应随着腔宽比的增大而减弱。不同腔宽比条件下轴承的启动轨迹如图12(c)所示,由于轴承浮起前的运动以沿轴表面的滑行为主,因而运动轨迹受腔宽比影响很小,而轴承浮起后,轴承轨迹范围随着腔宽比的增大而减小。 图12 不同腔宽比条件下轴承承载力和运动轨迹的变化 Fig.12 Variations of bearing load capacity and trajectory under different groove width ratios 图13 为轴承浮起转速和磨损范围随腔宽比的变化,由图可见,随着腔宽比的增大,轴承浮起转速增大而磨损范围减小。为减小轴承启动过程中的摩擦和磨损,腔宽比可取0.8。 图13 轴承浮起转速和磨损范围随腔宽比的变化 Fig.13 Lift-up speed and wear zone of bearing versus groove width ratio 图14 为轴承启动位置和启动力矩随腔深的变化。与腔宽比的影响类似,腔深的变化不改变轴承表面形貌参数及载荷,因而腔深对启动位置和启动力矩的影响很小。 图14 轴承启动位置和启动力矩随腔深的变化 Fig.14 Bearing starting-up position and starting-up torque versus groove depth 图15 为不同腔深条件下轴承启动过程中承载力和运动轨迹的变化。由图15(a)可见,随着腔深的增大,气膜承载力的最大值降低,且最大承载力出现所用时间增加。同时,轴承接触承载力呈现出随腔深的增大而快速减小的趋势。此外,由图15(c)可见,在浮起前的滑行阶段,不同腔深轴承的轨迹基本相同,而浮起后轨迹范围随着腔深的减小而增大。 图15 不同腔深条件下轴承承载力和运动轨迹的变化 Fig.15 Variations of bearing load capacity and trajectory under different groove depths 图16 轴承浮起转速和磨损范围随腔深的变化 Fig.16 Lift-up speed and wear zone of bearing versus groove depth 图16 为轴承浮起转速和磨损范围随腔深的变化,由图可见,随着腔深的增大,轴承浮起转速和磨损范围均呈现出先减小后增大的趋势。当腔深为1.0 μm 和2.0 μm 时,浮起转速和磨损范围分别有最小值。因此,为提高轴承启动特性,减小磨损范围,轴承腔深应取2.0 μm。 本文针对陀螺电机H 型动压气体轴承的启动过程,建立了考虑5 自由度运动方程、表面粗糙接触和润滑的分析模型,对轴承启动力矩、浮起转速、磨损范围等特性进行了分析,主要得到以下结论: 1)轴承启动前处于重力与表面接触承载力相平衡的静止状态,启动力矩为4.337×10-4Nm。在启动过程中,随着转速的升高,转子与轴接触面积逐渐减小,转速为754.9 r/min 时转子浮起,磨损范围约83.9°。 2)表面粗糙度对轴承启动特性有一定的影响。随着峰顶标准差的增大,浮起转速明显增大,而启动力矩和磨损范围受表面粗糙度影响有限。为提高轴承启动特性,可降低轴承峰顶标准差,提高轴承表面粗糙度加工等级。 3)腔宽比和腔深对启动位置和启动力矩影响不大。随着腔宽比的增大,浮起转速增大,但磨损范围减小。而随着腔深的增大,浮起转速和磨损范围均先减小后增大,当腔深为1.0 μm 和2.0 μm 时浮起转速和磨损范围分别最小。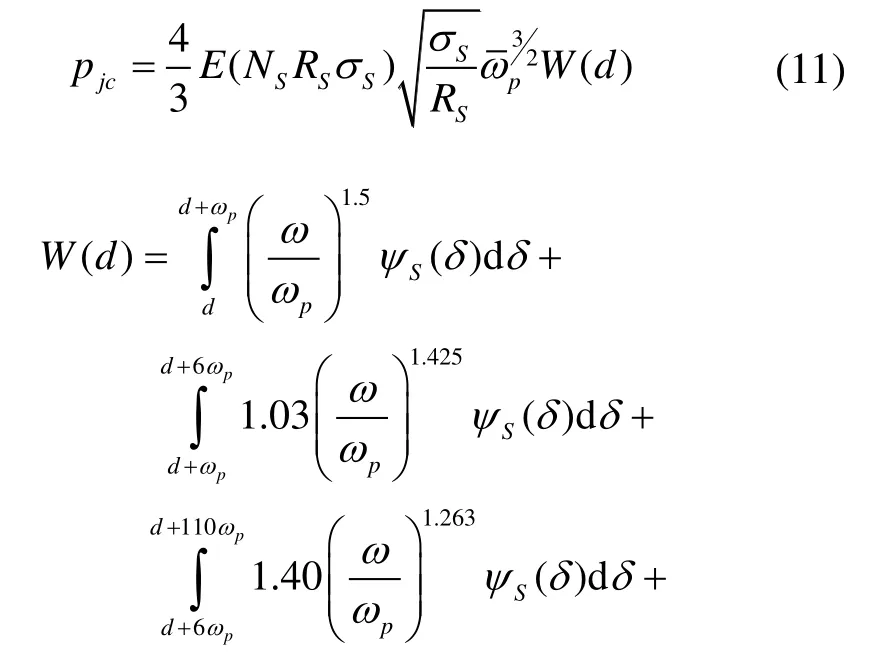

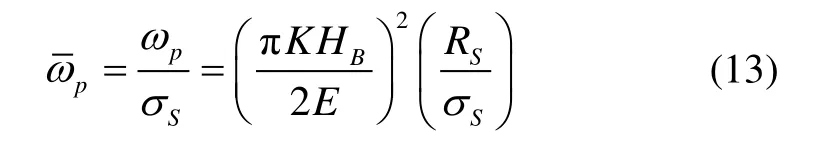

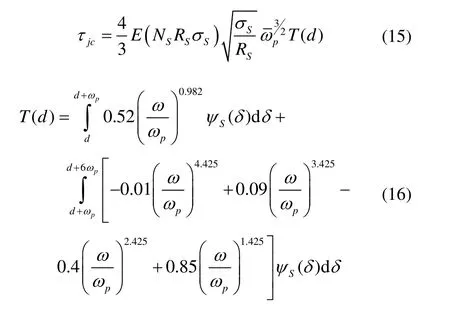
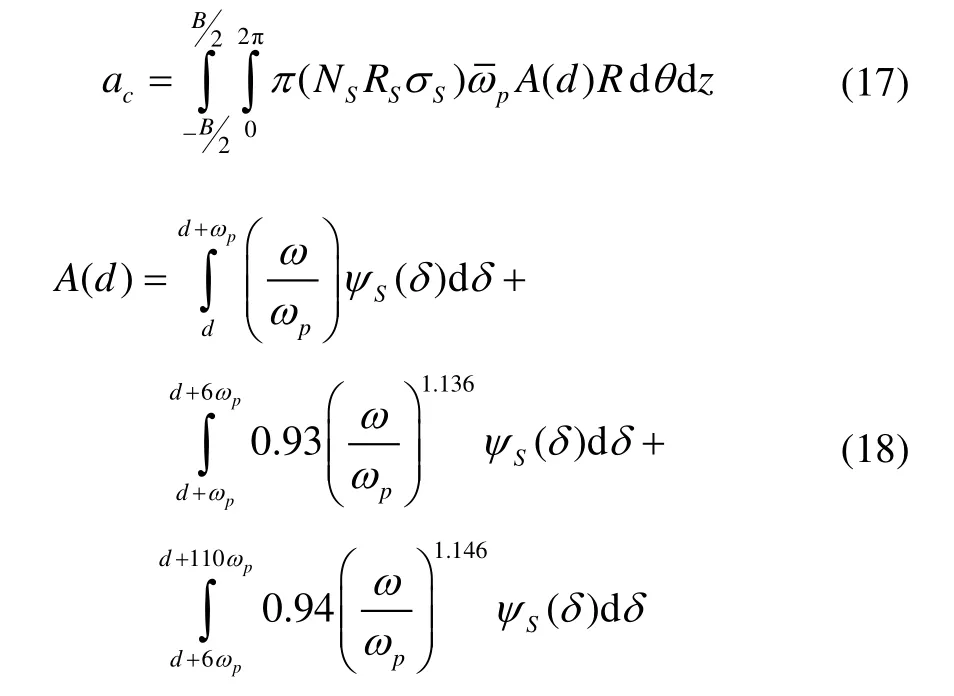
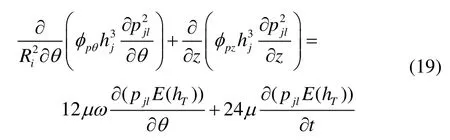




1.3 轴承反作用力
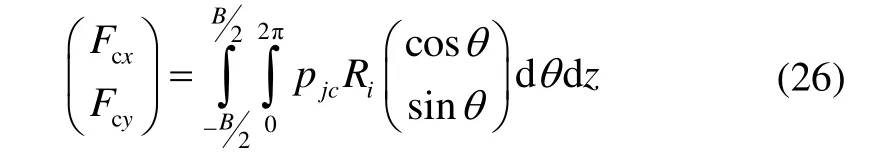
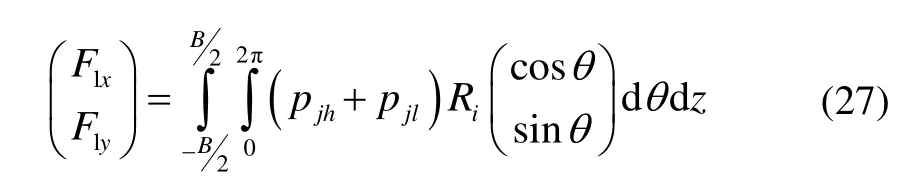
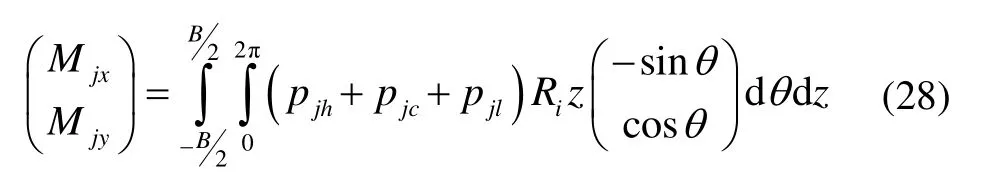
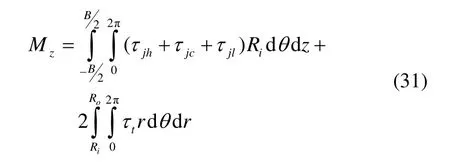

1.4 数值算法

2 结果与讨论
2.1 轴承启动特性分析



2.2 实验验证


3 轴承表面及结构参数影响分析
3.1 表面粗糙度的影响



3.2 腔宽比的影响



3.3 腔深的影响
4 结 论
