关于乘性噪声驱动的随机动力系统的中心流形的逼近

李 琴, 陈光淦, 杨 敏

(四川师范大学 数学科学学院, 四川 成都 610066)

稳定流形、不稳定流形和中心流形等不变流形刻画了动力系统演化的几何结构.Mohammed等[1]研究了由半鞅驱动的随机微分方程的稳定流形与不稳定流形;Boxler[2]和Roberts等[3]分别考虑有限维和无穷维随机微分方程的中心流形;Duan等[4]研究在指数二分性条件下利用Liapunov-Perron方法证明随机不变流形的存在性及其光滑性;Wong等[5-6]从数值模拟与计算机角度研究了随机微分方程的逼近；Acqistapace等[7]用光滑的Φε(t)去近似不光滑的W(t),得到随机微分方程的刻画；Shen等[8]通过平稳过程研究了Wong-Zakai型的近似.

本文考虑一类Stratonovich乘性噪声驱动的随机发展方程

(1)

其中,W(t)是Wiener过程,它处处连续,处处不光滑,“∘”表示Stratonovich乘积.系统(1)在通常乘积意义下的形式为

考虑随机系统

0<ε≪1.

(2)

1 预备知识

令H为无穷维可分的Hilber空间,其范数为|·|,内积为〈·,·〉.假定线性算子A:D(A)→H在Hilbert空间H上生成了一个强连续半群S(t):=eAt,并满足下面条件：

(A1) 指数三分性

|eAtPcv|≤Keγ|t||v|,t∈R,v∈H,

|eAtPuv|≤Keαt|v|,t≤0,v∈H,

|eAtPsv|≤Ke-βt|v|,t≥0,v∈H,

(3)

其中,α>γ>0>-γ>-β,K>0和I=Pc+Pu+Ps.记Hc=PcH,Hu=PuH和Hs=PsH,则有H=Hc⊕Hu⊕Hs.空间Hc、Hu和Hs分别被称为中心子空间、不稳定子空间和稳定子空间.

假设非线性项F(u)满足F(0)=0并且在H上满足

(A2) Lipschitz条件

|F(u1)-F(u2)|≤LF|u1-u2|,

(4)

其中LF>0是Lipschitz常数.

定义算子B:R→L(H),

定义 1.1设(Ω,F,P)是一个完备概率空间,θ={θt}t∈R是Ω上的变换族,定义映射

θ:(R×Ω,B(R)⊗F)→(Ω,F),

如果映射θt满足如下条件:

(i)θ0=idΩ;

(ii) 对t,τ∈R,有θt∘θτ=：θtθτ=θt+τ;

(iii) 映射(t,ω)→θtω是B(R×F,F)-可测,且对任意t∈R,有θtP=P,

则称(Ω,F,P,θ)为驱动动力系统.

定义 1.2设(H,dH)是一个完备度量空间,如果映射

φ:(R×Ω×H,B(R)⊗F⊗B(H))→(H,B(H))

满足下面性质:

φ(0,ω,x)=x,

φ(t+τ,ω,x)=φ(t,θtω,φ(t,ω,x)),

τ∈R,ω∈Ω,x∈H,

则称θ和φ构成的二元组(θ,φ)为一个随机动力系统.

定义 1.3对于随机动力系统φ(t,ω,x),如果对任意的t≥0,ω∈Ω有

φ(t,ω,M(ω))⊂M(θtω),

那么随机集M(ω)称为正不变集.

定义 1.4对于不变集M(ω),如果存在一个Lipschitz映射

hc(·,ω):Hc→Hu⊕Hs

满足

M(ω)=Mc(ω)={(ξ,hc(ξ,ω))|ξ∈Hc},

hc(0,ω)=0

和相切条件,即导数Dhc(0,ω)=0,对每一个ξ∈Hc,hc(ξ,·)是可测的,Hc、Hu、Hs如条件(A1)中所定义,那么M(ω)称为一个中心流形.

考虑一个Langevin方程

(5)

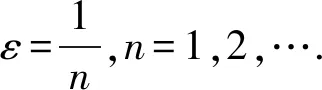
它具有轨道不变性和测度不变性[9].定义

引理 1.1[7]设W(t)是R上的一个布朗运动,那么对每一个固定的T>0,当ε→0时,Φε(t)在[0,T]上几乎处处一致收敛到W(t).

引理 1.2[9]假设zε(θtω)是Langevin方程(5)的解,那么

作变换T(ω,x)=xe-εzε(ω),方程(1)转化为

G(θtω,vε),v(0)∈H,

(6)

其中G(ω,x)=e-εzε(ω)F(eεzε(ω)x).显然,对任意固定的ω∈Ω,函数G和F有相同的Lipschitz常数LF.

引理 1.3[10]假设vε是方程(6)生成的随机动力系统,那么

T-1(θtω,vε(t,ω,T(ω,u0)))=:u(t,ω,u0)

也是一个随机动力系统.对任意u0∈H,随机过程:(t,ω)→u(t,ω,u0)是方程(1)的解.

2 中心流形的Wong-Zakai型逼近

2.1 中心流形的存在性首先证明随机系统(6)和(2)中心流形的存在性.

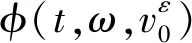
对正数η∈[γ,min{β,α}],定义2个Banach空间

Cη(ω):={φ∈C(R,H):

其范数为

|φ(·)|Cη=

以及

Cη,ε(ω):={φ∈C(R,H):

其范数为

令

Mvε,c(ω)={x∈H|φ(·,ω,x)∈Cη,ε};

MXε,c(ω)={x∈H|φε(·,ω,x)∈Cη,ε}.

引理 2.1[3]如果LF满足

(7)

那么系统(6)有不变的Lipschitz中心流形

Mvε,c(ω)={(ξ,hvε,c(ξ))|ξ∈Hc},

其中,hvε,c(·,ω):Hc→Hu⊕Hs为Lipschitz连续映射,并且

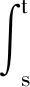
用文献[3]中类似的方法可得到系统(2)的中心流形.

引理 2.2如果LF满足

那么系统(2)有不变的Lipschitz中心流形

MXε,c(ω)={(ξ,hXε,c(ξ))|ξ∈Hc},

其中,hXε,c(·,ω):Hc→Hu⊕Hs为Lipschitz连续映射,并且

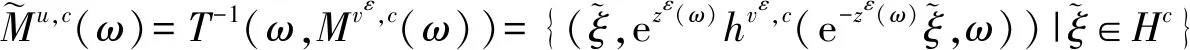
2.2 中心流形的Wong-Zakai型逼近

引理 2.3设hu,c与hvε,c分别为系统(1)和(6)的中心流形映射,当ε→0时,那么

|hu,c(ξ,ω)-hXε,c(ξ,ω)|→0, a.s..

证明设u(t)和vε(t)分别是系统(1)和(6)的解.对于u(t),由引理1.3知

u(t,ω,u0)=eεzε(θtω)vε(t,ω,u0e-εzε(ω)).

系统(6)在中心流形上的解vε(t)[3]有如下表达式

vε(t)=ΨA(t,0)Pcvε0+

(8)

其中

对应的中心流形的映射为

hvε,c(ξ,ω)=

(9)

由u(t,ω,u0)=eεzε(θtω)vε(t,ω,u0e-εzε(ω)),得u(t)的中心流形的映射为

hu,c(ξ,ω)=eεzε(ω)hvε,c(e-εzε(ω)ξ,ω).

(10)

因为hvε,c(ξ,ω)关于Lipschitz连续的,而且当ε→0,e-εzε(ω)→1.

易知,当ε→0时有

hu,c(ξ,ω)-hvε,c(ξ,ω)=

eεzε(ω)hvε,c(e-εzε(ω)ξ,ω)-hvε,c(ξ,ω)→0,

得证.

引理 2.4假设条件(A1)、(A2)与(7)式成立,并且hvε,c与hXε,c分别为系统(6)和(2)的中心流形映射.当ε→0时,那么

|hvε,c(ξ,ω)-hXε,c(ξ,ω)|→0, a.s..

证明系统(2)在中心流形上解Xε(t)为

Xε(t)=eAt+Φε(t)PcXε0+

(11)

对应的中心流形映射为

hXε,s(ξ,ω)=

(12)

由引理2.1和2.2知

|hvε,c(ξ,ω)-hXε,c(ξ,ω)|=

e-εzε(θsω)F(vε(s))+

e-εzε(θsω)F(vε(s))-F(vε(s))+

F(vε(s))F(Xε(s))]ds|≤

(e-εzε(θsω)-1)]ds|+

F(Xε(s))]ds|:=I1+I2.

对于I1,由指数三分性假设可得

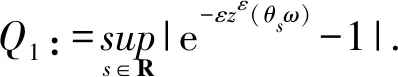
由引理1.1知-εzε(θtω)=Φε(t)-W(t),可得当ε→0时,Q1→0.这说明当ε→0时,I1→0.

对于I2,由指数三分性假设可得

如果能够证明,当ε→0时,

|vε(·)-Xε(·)|Cη,ε→0,

就可得到I2→0,从而证得结论.因此,下面证明|vε(·)-Xε(·)|Cη,ε→0.

|Xε(t)-vε(t)|≤

F(Xε(s))|ds+

F(Xε(s))|ds≤

I21+I22+I23+I24+I25+I26,

(13)

那么

I22+I23+I24+I25+I26).

(14)

对于I21有

2KLF|vε(s)||e-εzε(θs)-1|ds≤

2KLF|vε(·)|Cη,ε×

(15)

对于I22有

e-η|t|-Φε(t)I22≤e-η|t|-Φε(t)×

|Xε(·)-vε(·)|Cη,εeη|t|+Φε(s)ds≤

KLF|Xε(·)-vε(·)|Cη,ε×

(16)

类似地,对于e-η|t|-Φε(t)I23、e-η|t|-Φε(t)I24、e-η|t|-Φε(t)I25和e-η|t|-Φε(t)I26有

e-η|t|-Φε(t)I23≤

(17)

e-η|t|-Φε(t)I24≤KLF|Xε(·)-

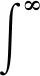
(18)

e-η|t|-Φε(t)I25≤

(19)

e-η|t|-Φε(t)I26≤KLF|Xε(·)-

(20)

由(15)、(17)和(19)式,可得当ε→0时,

再由(16)、(18)和(20)式可得

|Xε(·)-vε(·)|Cη,ε×

从而由(14)和(7)式有

|hvε,c(ξ,ω)-hXε,c(ξ,ω)|→0,

得证.

定理 2.1假设条件(A1)、(A2)与(7)式成立,且hu,c与hXε,c分别为系统(1)和(2)的中心流形映射.当ε→0时,那么

|hvε,c(ξ,ω)-hXε,c(ξ,ω)|→0, a.s..

由引理2.3和2.4,易得定理2.1成立.