一类含有未知导函数的积分不等式中未知函数的估计

范乐乐, 王五生, 钟 华

(河池学院 数学与统计学院, 广西 宜州 546300)

Gronwall-Bellman[1-2]为了研究微分方程的解对参数的连续依赖性考虑了下面的积分不等式

其中c≥0是常数,给出了未知函数的估计

(1)

人们发现Gronwall-Bellman型积分不等式及其推广形式是研究微分方程、积分方程和微分-积分方程解的存在性、有界性和唯一性等定性性质的重要工具,因此致力于研究它的各种推广形式,使它的应用范围不断的扩大.大部分数学工作者研究积分号内不含未知函数的导函数的积分不等式[3-12].由于积分号内包含未知函数及其导函数的积分不等式在研究微分-积分方程中具有重要作用,Pachpatte[13]研究了下面的积分号内含有未知函数及其导函数的线性积分不等式

t∈R+,

(2)

和

(3)

Akin-bohner等[14]在此基础上进一步研究了时标上的线性积分不等式

t∈T0,

(4)

和

uΔ(t)≤a(t)+b(t)(u(t)+

(5)

Zareen[15]更进一步研究了积分号内含有未知函数及其导函数的非线性积分不等式

t∈R+.

(6)

本文受文献[13-15]的启发,研究了积分号外具有非常数因子,且积分号内含有未知函数及其导函数的非线性积分不等式

u2(s))ds),t∈R+.

(7)

不等式(7)把文献[13]中的不等式(3)推广成非线性积分不等式,把文献[15]中的不等式(6)推广成积分号外具有非常数因子的积分不等式.本文给出了不等式(7)中未知导函数的估计,举例说明了本文结果可以用来研究相应类型的微分-积分方程解的性质.

1 主要结果与证明

为了简化本文主要结果的证明过程,先给出一个引理.

引理 1假设函数u(t)、a(t)、b(t)、c(t)、d(t)都是定义在R+=[0,∞)上的非负连续函数,且满足不等式

d(t)u3(t),t∈R+.

(8)

如果u(0)>0,

则有未知函数u(t)的估计式

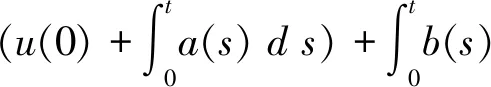
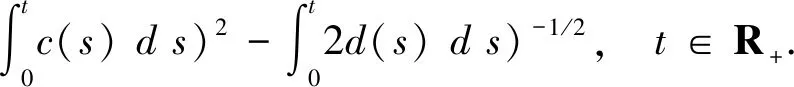
证明先把不等式(8)中的t改写成s,然后两边关于s从0到t积分,得到

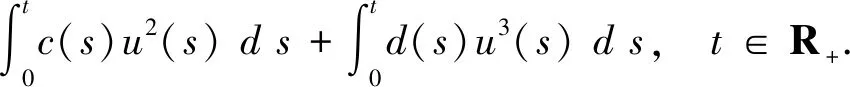
对于任意非负实数T,由不等式(10)可以看出

把不等式(11)右端定义成函数v(t),即

由定义式(12)可以看出

t∈[0,T].

(13)

求函数v(t)的导函数得

b(t)v(t)+c(t)v2(t)+d(t)v3(t),t∈[0,T]. (14)

不等式(14)两边同除以v(t)得到

t∈[0,T].

(15)

先把不等式(15)中的t改写成s,然后两边关于s从0到t积分,得到

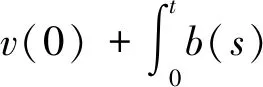
(16)

把不等式(16)的右端定义为函数w1(t),即

(17)

由(16)和(17)式可以看出w1(t)是非负连续增函数,且满足

v(t)≤ew1(t),t∈[0,T].

(18)

求函数w1(t)的导数得到

c(t)ew1(t)+d(t)e2w1(t),t∈[0,T]. (19)

不等式(19)两边同乘以-e-w1(t)得到

t∈[0,T].

(20)

先把不等式(20)中的t改写成s,然后两边关于s从0到t积分,得到

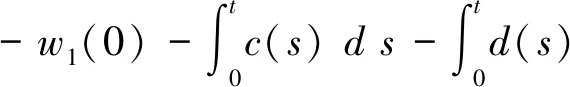
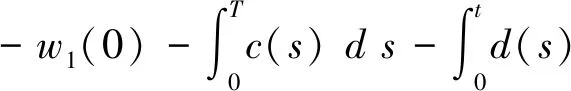
t∈[0,T].

(21)

把不等式(21)的右端定义为函数w2(t),即

t∈[0,T].

(22)

可以看出

(23)

求函数w2(t)的导数

t∈[0,T],

(24)

不等式(24)两边同乘以w2(t)得到

(25)

把不等式(25)两边积分得到

由(13)、(18)、(23)和(26)式,推出

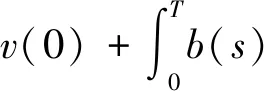
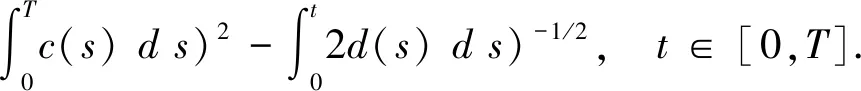
在(27)式中令t=T,得到

(28)

由于T的任意性,(28)式可以写成

u(t)≤((exp(-(ln(u(0)+

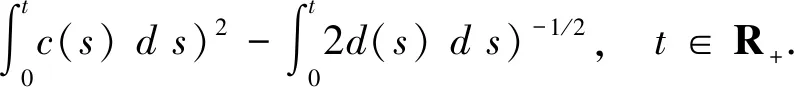
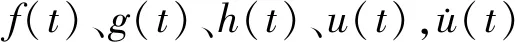
(30)

则有未知导函数的估计式

(31)

证明由不等式(7)定义函数m(t),

u2(s))ds,t∈R+.

(32)

由不等式(7)和(32)式可以看出

m(0)=u(0),u(t)≤m(t)

(33)

和

(34)

求函数m(t)的导数

f(t)+g(t)m(t)+h(t)(f(t)+g(t)m(t))2+

h(t)(f(t)+g(t)m(t))m2(t)=

f(t)+h(t)f2(t)+(g(t)+2h(t)f(t)g(t))m(t)+

(h(t)g2(t)+h(t)f(t))m2(t)+

h(t)g(t)m3(t),t∈R+.

(35)

把引理应用于不等式(35)得到

(36)

由(34)和(36)式得到所求的估计(31)式.

2 应用

本文结果可以用来研究相应类型的微分-积分方程解的性质.现在考虑微分-积分方程

x(0)=c.

(37)

推论 1假设|c|是正常数,H∈C(R×R×R,R)满足下列条件

(38)

f(t)、g(t)、h(t)满足定理的要求.如果x(t)是方程(37)的解,那么有方程解的模的估计式

(39)

证明利用条件(38),由方程(37)推出

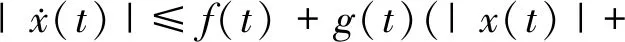
t∈R+.

(40)

由于(40)式具有不等式(7)的形式,且满足定理中的相应条件,利用定理就可以得到所求的方程解的模的估计式(39).