板桩入土深度计算方法探讨
2019-11-19王文杰杨火其孙逸豪
王文杰,杨火其,孙逸豪
(浙江省水利河口研究院,杭州 310020)
经典的土力学书籍均将板桩的土力学计算与挡土墙编写在一起,其基本思路是板桩因桩后承受土压力而发生水平移动的趋势,使板桩两侧分别产生主动和被动土压力,然后采用力和力矩平衡条件建立方程,再利用已知条件联立解出板桩的入土深度。基于这一思路,目前普遍采用图解法求解。这种解题方法基本上都假定板桩为刚性物体。对于截面尺寸较大且长度较短的板桩,这样做基本符合实际,但对于截面尺寸较小且长度较长的板桩,则该假定便显得不尽合理,此时应将其视作弹性物体考虑。《土力学》教材采用板桩发生弹性变形的力学模型推导出板桩入土深度计算方程组的,但该方程组存在两个方面的问题:其一是它采用力和力矩极限平衡条件建立方程式,所得结果是极限平衡解,并没有考虑到工程设计中常用的安全系数,所以无法在工程设计中直接采用。

1-a 板桩计算模型 1-b 板桩变形图1 板桩受力分析简图Fig.1 Sheet pile stress analysis
本文根据武汉水利电力大学出版的《土力学》[2]中的板桩受力模型,重新推导出力和力矩极限平衡方程式,然后参照有关规范,采用稳定安全系数对力和力矩极限平衡方程进行修正,得出可供工程设计者直接应用的板桩入土深度计算方程。
1 板桩受力情况分析
图1-a是较常见的板桩受力情况,将多根板桩扣接起来便成为板桩墙,它可用作永久性或临时性的挡土结构,属于受弯构件,其挠度曲线如图1-b所示。
板桩的结构形式可分为悬臂式与锚定式两大类,本文仅就如图1-a、1-b所示的悬臂式板桩进行分析。
板桩受水平力F作用而发生变形,使紧邻地面以下一段板桩所受的土压力与F力反向,而更深处的板桩所受的土压力又与F力同向,如图1-a所示。由于土压力是板桩推动土体而产生的,所以合压力应为被动土压力和主动土压力之差。假定合压力从地面向下按(EP-EA)比例线性增大到某点m达到最大值,此点距桩底端的距离为z,然后按线性比例减小到零,至n点,此点距桩底端的距离为z′,再往下则合压力反向,且逐渐按线性比例增大,至桩底端达到最大。
2 板桩极限平衡方程式的推导
根据学者们的研究[3-10],板桩稳定与多种因素有关,如抗力系数、桩基承载力、分项系数、承载力可靠指标等,均对板桩的稳定性产生影响,需要综合分析研究。
2.1 土压力及力臂
如图1-a所示,板桩受3个力的作用而处于极限平衡状态,即向左的集中力F、浅层向右的三角形分布力和深层向左的三角形分布力。
(1)向左的集中力。
集中力F的作用点在板桩顶端,计算时将地面以上部分的土压力转换成等效的集中力。力臂(系指力的作用点距板桩底端距离,下同)为(h+d)。
(2)浅层向右力。
m点以上部分力
该力力臂为
m点以下部分力
该力力臂
(3)深层向左力。
该力力臂
2.2 极限平衡方程式的推导
力以向左为正,力矩以逆时针方向旋转为正。
力极限平衡方程
整理后得
(1)
力矩极限平衡方程
整理后得
(2)
式中:z为浅层与F反向的土压力最大值距桩底端的距离,m;
d为板桩外侧刷深后的滩面距桩底端的距离,m;


h为桩顶距刷深后滩面的距离,m;
F为桩顶集中力,将滩面以上部分土压力转换成等效集中力,kN/m;
γ为土体容重,水下用浮容重,kN/m3;
Ka为主动土压力系数,Ka=tan2(45-φ/2);
Kp为被动土压力系数,Kp=tan2(45+φ/2);
c为土内聚力,kPa;
φ为土的磨擦角,(°)。
3 板桩入土深度方程
方程式(1)和(2)是板桩处于极限平衡条件下导得的方程式,所以不能在工程设计中直接应用。根据《地基基础设计规范》规定,抗水平滑动稳定安全系数KF≥1.3,抗倾覆稳定安全系数KM≥1.5。显然,力平衡方程式中的向左力促使板桩发生水平滑动,而向右力则阻止板桩发生水平滑动,故可在该方程式的各向左力项中分别乘以抗水平滑动稳定安全系数KF,其值可取1.3;力矩平衡方程中逆时针旋转的力矩促使板桩发生倾覆,而顺时针旋转的力矩则为阻止板桩发生倾覆,故可在各逆时针力矩项中乘以抗倾覆稳定安全系数KM,计算时可取1.5。用上述系数对方程式(1)和(2)进行修正,则得工程设计中计算板桩入土深度方程为
(3)
(4)
式中:KF为抗水平滑动稳定安全系数,据《地基础设计规范》规定,KF≥1.3;
KM为抗倾覆稳定安全系数,据《地基基础设计规范》规定,KM≥1.5;其余符号同前。
方程式(3)和(4)便是计算板桩入土深度d的方程式,方程组中未知数为d和z,由于该方程组为二阶拟线性方程组,故一般采用试算法求解。根据《理论土力学》(美)太沙基著板桩计算一章,板桩实际入土深度值可将计算值放大20%,即为1.2 d。
4 板桩最大弯矩确定
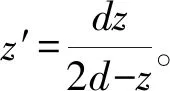
根据《材料力学》,最大弯矩发生在剪切力为零处(即图1中的n点),该断面弯矩为

(5)
5 板桩入土深度方程式验证
用《工程地质手册》(第五版)第二章关于悬臂支护桩设计一节的计算实例来验证板桩入土深度方程的有效性。
该书介绍了常用的三种方法—图表法、图解法和试算法。其中试算法的基本思路大体与作者的类同,即均考虑了稳定安全系数和板桩入土深度的附加值。现利用该书P798页例题二,分别用试算法和本文的方法进行计算。

图2 板桩计算非弹性模型Fig.2 Sheet pile calculation inelastic model
5.1 试算法
(1)解题步骤。
如图2所示,试算步骤分为:
①先假定插入深度为d1,计算绕e点的力矩,使净被动土压力DEF所产生的抵抗力矩为净主动土压力ACD所产生力矩的1.5~2.0倍;
②然后将d1增加15%,作为实际需要的插入深度。
(2)计算实例。
选取《工程地质手册》(第五版)P798页的例题二。
①已知条件。
表面均布荷载q=9 kN/m3,H=6.5 m,c=0,φ=30°,地下水高程-5.5 m,湿容重γ=18 kN/m3,浮容重γ′=8 kN/m3。
②计算步骤及结果。
设d1=11 m,则绕e点逆时针力矩Me=253 kN·m,顺时针力矩Me=276 kN·m,安全系数k=1.09<1.5,不满足要求。
再设d1=12.5 m,则绕点逆时针力矩Me=283 kN·m,顺时针力矩Me=434 kN·m,安全系数k=1.53>1.5,满足要求。故实际入土深度d=12.5×1.15=14.38 m。
5.2 作者方法
(1)计算条件。
计算条件同上。
(2)计算结果。
运用本文介绍的方程式(3)~(4),采用计算机计算得d1=11.7 m,板桩实际入土深度d=11.7×1.15=13.5 m。
由此可知,两者计算结果相近,说明本文介绍的方程可在工程初步设计中应用。
6 应用实例
本文作者在承担《浙江省上虞市标准海塘工程(吕家埠—花宫段)初步设计》课题任务时,对底脚防冲方案比较曾进行板桩结构计算及技术经济比较,板桩入土深度及最大弯矩计算时采用方程(3)~(5)。从工程多年运行情况看,计算结果安全可靠。计算过程如下:
(1)计算条件。
板桩顶高程3.0 m(1985国家基准,下同),板桩出露高度3.0 m;设计低水位3.05 m,故采用浮容重,γ=7.6 kN/m3;土体的力学指标为c=14.6 kPa,φ=6.1°。
(2)计算结果。
将以上已知条件代入方程式(3)~式(5),采用试算法求得d=4.2 m,z=2.76 m,Ep=220 kN/m,EA=26.5 kN/m,F=5.0 kN/m,Mmax=260 kN·m。
板桩护脚措施已在浙江省钱塘江海塘北岸险段标准塘工程海宁段建设中被采用。它既能防止底脚淘刷,又能适当提高海塘整体稳定性。
7 结论
本文根据板桩受力分析,采用极限平衡方程式,推导出板桩入土深度方程,然后采用《工程地质手册》中的相关算例进行验证,计算结果与其相近。最后,采用工程实例对板桩入土深度方程进行应用。结果表明,经过工程多年运行实践,认为计算结果安全可靠。
