宽带啁啾光纤光栅F-P腔磁场传感器研究*
2019-11-18吴梓楠唐冬林张旭辉代志勇
吴梓楠, 唐冬林, 张旭辉, 代志勇
(1.西南石油大学 机电工程学院 石油天然气装备教育部重点实验室,四川 成都 610500;2.电子科技大学 光电信息学院 光电传感与信息处理重点实验室,四川 成都 610054)
0 引 言
微弱磁场探测技术在诸如雷区以及武器的扫描搜索、舰船的磁隐形与潜艇的磁探测、利用磁制导导弹与磁导航等领域都有广泛的运用。在诸多的磁场探测技术中,光纤磁场传感器具备了灵敏度高、抗电磁干扰能力强、动态范围大、快速响应、结构紧凑体积小、绝缘防爆、交直流可测,可通过构建阵列进行矢量测量等优异特点。自1980年Yariv A教授首次提出利用磁致伸缩效应测量微弱磁场,并预测最小可探测磁场能够达到1.6×10-12T[1],有关光纤微弱磁场传感技术大量研究相继见报[2~4]。1981年,Trowbridge F R等人成功研制出以金属玻璃作为磁致伸缩材料的光纤微弱磁场传感器[5]。1983年,美国海军实验室的Koo等人成功研制了基于马赫—曾德(Mach-Zehnder,M-Z)干涉仪的光纤磁场传感器,并且通过实验分析验证了磁性材料的磁致伸缩量与外加磁场信号之间成平方正比。此外,为了改进系统的信噪比,还采用高频调制信号的方式,使系统性能大幅度地优化,获得了10-6T/Hz1/2的探测灵敏度。在此基础上,Bucholtz等人进行了一系列的改进,在单轴向的M-Z干涉仪传感臂上同时加载3只换能器,换能器彼此正交并且利用不同频率的高频信号进行调制,实现了3个垂直方向上的信号检测。
相较于国外,国内的研究起步较晚。2000年,文献报道了姚寿铨等人制作出基于M-Z干涉仪的光纤微弱磁场传感器,将8 cm长的磁致伸缩片粘贴在12 cm的干涉臂上,保证了干涉臂内的光场具有相对稳定的偏振状态。2001年,电子科技大学的薛志英[6]利用M-Z干涉仪,基于超磁致伸缩材料设计了光纤微弱磁场传感器,探测灵敏度可达2.86×10-10/Hz。2018年,沈涛等人将单根光纤的马赫—曾德尔模间干涉结构和双臂马赫—曾德尔干涉结构结合,实现模间干涉的马赫—曾德尔磁场传感器[7]。虽然目前的研究取得了丰硕的成果,但依然存在信号解调复杂、灵敏度不够高、稳定性差、体积大等问题。
为了解决现有光纤磁场传感器解调方法复杂、体积过大、稳定差等问题,本文提出并设计了一种结合反射光谱分析方法的宽带啁啾光栅F-P腔全光纤微型磁场传感器。实验测试表明该磁场传感器的相位灵敏度为1.62 rad/μT,平均测量误差为0.43 μT,测量误差方差为0.3 μT。
1 传感器的工作原理与特性分析
研制的啁啾光纤光栅F-P腔磁场传感器的系统结构如图1所示。ASE宽带光源发出的光通过耦合器进入到啁啾光纤光栅F-P腔中,反射回干涉光通过耦合器进入到光谱仪中,再通过微型计算机对采集到的光谱信号进行分析与处理。

图1 磁场传感器系统结构
1.1 宽带啁啾光纤光栅F-P腔
啁啾光栅是一种特殊结构的光纤光栅,光栅周期随轴向发生变化,从而构成宽带反射光谱。其布拉格波长λB不再是一个常数
λB(z)=2neff(z)Λ(z)
(1)
式中Λ为光栅周期,neff为光栅有效折射率。
将一非均匀的光纤光栅看作是由m小段光纤光栅级联构成,并且把每一小段光栅看作是近似均匀的,则第i段光纤光栅的传输矩阵Fi可以表示为
Fi=
(2)
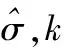
(3)
式中λD=2neffΛ为第i段光栅的布拉格波长,Δneff为折射率的调制深度,C为啁啾系数。其中γ由下式决定
(4)
将每段准均匀光栅的传输矩阵相乘,即可得到整段非均匀光栅的传输矩阵。
在同一段光纤中连续串入2个相同的线性啁啾光纤光栅(linear chirped FBG,LCFBG)就构成了啁啾光纤光栅F-P腔,其结构如图2所示。
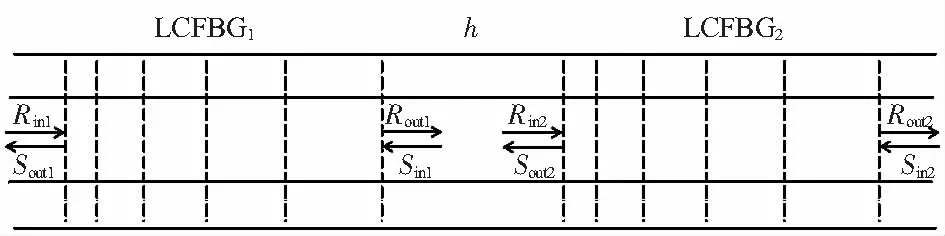
图2 啁啾光纤光栅F-P腔示意
利用传输矩阵法,将构成F-P腔的2个LCFBG单元的传输矩阵相乘,即可得到F-P腔的传输特性,由F-P腔入射端的光波场推算出F-P腔出射端的光波场。F-P腔传输矩阵
(5)
式中P=exp(-iβh),β=2nπ/λ为传播常数,n,λ分别为纤芯的折射率和真空波长,h为F-P腔的腔长。ρ1,ρ2分别为LCFBG1和LCFBG2的反射系数,τ1,τ2分别为LCFBG1和LCFBG2的透射系数。R,S分别为前向传输模式和后向传输模式。
根据上文推导的传输矩阵,利用MATLAB进行仿真,对啁啾光栅F-P腔的干涉光谱特性进行分析。仿真使用的啁啾光纤光栅的参数如下:光栅长度L=8 mm,有效折射率neff=1.45,折射率调制深度Δneff=2×10-3,折射率调制的条纹可见度v=1,中心波长λ0=1 550 nm,啁啾系数C=5 nm/cm。图3为不同腔长的啁啾光栅F-P腔干涉光谱图。仿真结果表明:随着腔长的增长,干涉条纹间距减小,干涉条纹数量增多。干涉条纹数量增多意味着有更高的传感精度,其光谱数据测试也就需要更高的光谱分辨率。
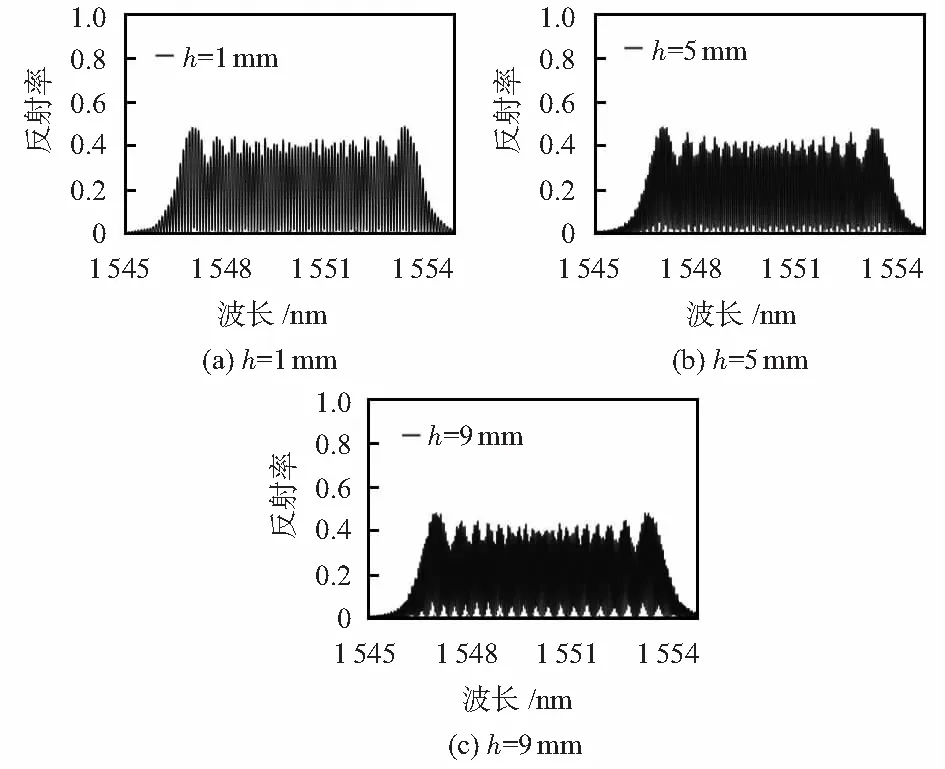
图3 不同腔长的啁啾光栅F-P腔干涉图谱
图4是不同光栅长度的啁啾光栅F-P腔的反射光谱特性图。其他参数不变,腔长为3 mm。仿真结果表明:随着光栅长度的增加,啁啾光栅的反射光谱变宽,对应的F-P腔的干涉光谱也变宽,干涉条纹间距变小,形成的干涉条纹变密,意味着可以获得的相位灵敏度越高。
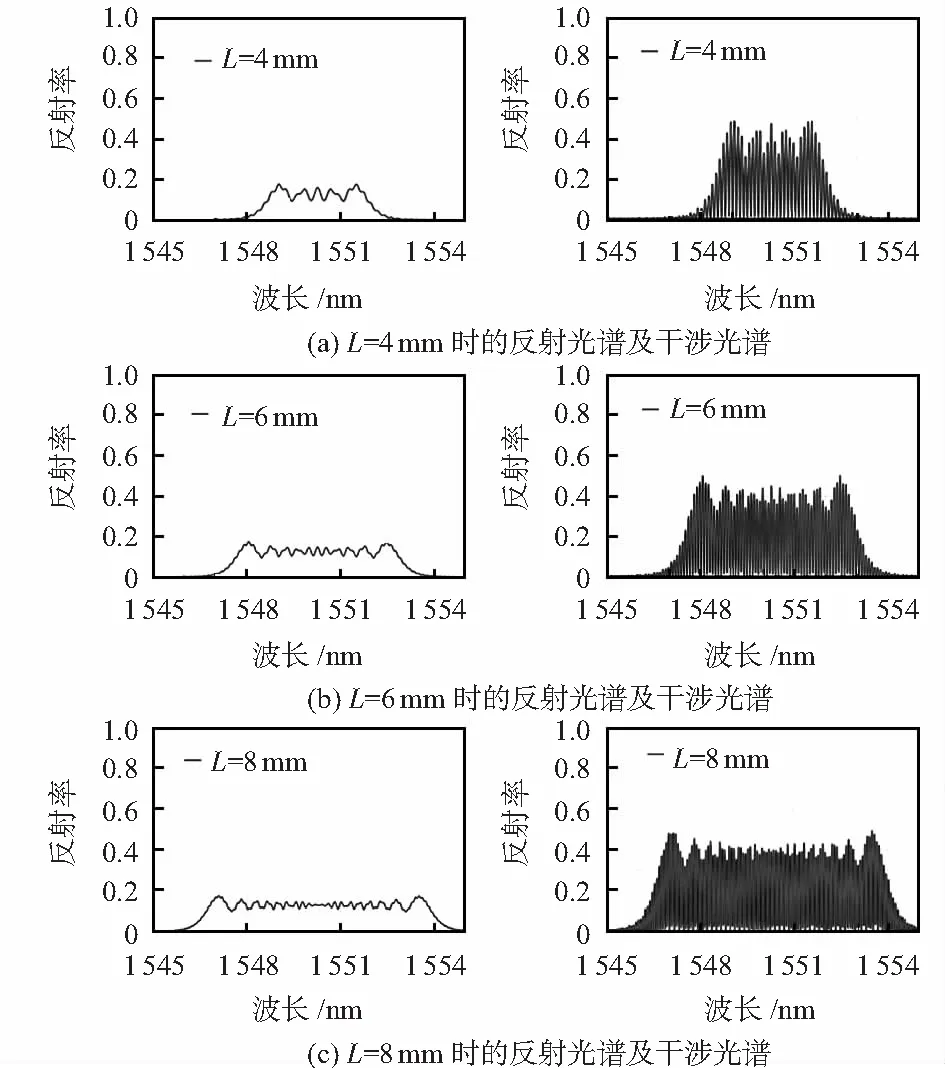
图4 不同光栅长度的啁啾光栅的反射光谱(左)以及其构成的F-P腔的干涉光谱图(右)
综上所述,该结构能够获得较好的干涉效果。理论上来说,腔长和光栅长度越大越好,但由于目前光谱仪分辨率的限制,无法实现更高精度的分辨,因此,综合各方面考虑,本实验中设置腔长为3 mm、光栅长度为8 mm。
1.2 磁致伸缩材料特性分析
磁性物质在外磁场的作用下尺寸伸长或者缩短,在去掉外磁场后尺寸恢复原状,这一现象称为磁致伸缩效应[8~11]。根据相干旋转理论,当测量方向与磁场方向有一定角度的情况下,磁致伸缩量与磁场的关系满足下列条件
(6)
式中HA为各向异性场,其大小由材料类型和退火条件决定,φ为磁场方向与材料长度方向的夹角,λs为饱和磁致伸缩量,Ceff为有效磁致伸缩系数。
本实验中,选用的磁性材料为Terfenol-D(成分为Tb0.27Dy0.73Fe2),外形尺寸为10 mm×5 mm×0.2 mm,将传感光纤粘贴在磁致伸缩材料上构成磁换能器。从式(6)可知,如果得知有效磁致伸缩系数Ceff,就可以根据磁致伸缩量ε求出磁场。
本实验通过迈克尔逊干涉仪对该换能器的应变特性进行了测量,再通过数据拟合得到磁致伸缩量ε和磁场的关系
ε=-20.061 77+3.112 12H+0.058 54H2
(7)
对比式(6)、式(7)中不仅有二次项,还存在一次项和直流常数项。是因为将不接通电流时测量得到的测量数据视为磁场为零时的磁致伸缩量,但此时磁场并不为零,所以拟合函数多出了负直流常数项;另一方面,通电螺线管的长度有限,由于尺寸的限制使得由通电螺线管产生的磁场分布不均匀且有限的,所以拟合函数中出现了一次项。但这些因数只改变拟合曲线的位置,并不会对曲线的形状造成影响,仍可以使用二次项系数表示磁致伸缩的系数,即本实验中有效磁致伸缩系数Ceff为0.058 54。综上,用这种方法测量得到的磁致伸缩系数是可靠的,磁致伸缩带来的非线性效应并不会对实验结果产生影响。
2 实验结果
2.1 实验系统
实验系统如图1所示。本实验中光源采用的是EXFO公司的ASE型宽带光源,波长范围为1 524~1 604 nm,功率为18.6 mW。光谱分析仪为日本YOKOGAWA公司的AQ6370C型,波长扫描范围设定为1 545~1 555 nm,波长分辨率设为0.02 nm,采样点数为500个。光纤F-P腔为自制的啁啾光纤光栅F-P腔,腔长为3 mm,光栅长8 mm,中心波长1 550 nm,啁啾系数5 nm/cm。为了产生微弱的磁场,实验中使用了通电螺线管,其为175匝无芯铜线圈,电源型号为MPS—3002L—3,输出电压范围0~30 V,输出电压精度为0.1 V,输出电流范围0~2 A,输出电流精度为0.1 A。磁通门磁强计(CTM—6W)作为参考仪器,工作磁场范围-82 026.5~82 026.5 nT。该系统具体的工作方式如下:宽带光源发出的信号光经过耦合器传输到光纤中,当有磁场产生时,粘贴在光纤表面的磁换能器将磁场能转换为机械能,由于超磁致伸缩材料的伸缩间接导致了光纤F-P腔在纵向上的应变。光纤F-P腔腔长的变化对信号光的传输产生了影响,从而导致了其干涉光谱的变化。利用光谱分析仪对变化后的干涉光谱进行采集,再利用微型计算机对该信号进行处理,通过解调算法,最终实现对待测磁场的测量。
2.2 信号处理与分析方法
条纹计数解调算法是利用干涉光输出光强和干涉相位之间的关系实现腔长解调。由于设计中采用的啁啾光纤光栅具有很低的反射率(R≪1),因此,将干涉光的输出光强表达式简化为
(8)
设干涉输出条纹的第m级和第m+n级极大值处对应的波长分别为λm和λm+n,则有关系
(9)
根据式(9)可以得到腔长h的表达式
(10)
依据式(10),通过对干涉谱的解调,可以得到腔长h。而且表达式中不含光强,可以忽略光强波动对腔长求解的影响,求解的准确性主要由干涉输出条纹的峰值波长准确性决定。测量出无磁场状态下的腔长h0,则可得磁致伸缩量ε=|h-h0|。代入式(6)中,即可计算出待测磁场H。
实验中的磁场信号是由通电螺线管产生的,磁场强度的大小可以通过控制通电螺线管中的电流进行调节,磁场从0 μT开始,每隔10 μT记录一次光谱数据,直到80 μT为止。在磁场从0 μT增大至80 μT的过程中,F-P传感器的腔长从18.365 0 mm伸长至18.375 9 mm。磁场每增大10 μT,腔长的平均伸长量为1.35 μm。通过微弱磁场探测实验,计算得到该光纤光栅F-P腔传感器系统的相位灵敏度为1.62 rad/μT。
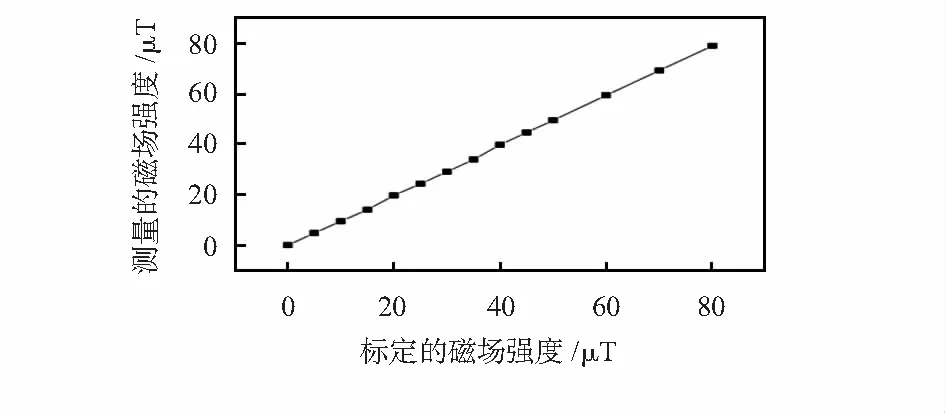
图5 测量结果与标定值对比
在整个实验中,磁场的制造与测量都是在恒温、恒压的环境中进行的,以减少系统误差。磁场探测实验中测量的结果与标定值的关系如图5所示,结果表明:光纤F-P腔磁场传感器探测得到的结果与标定值基本呈线性关系。经过计算,得到测量误差的平均值0.43 μT,测量误差的方差为0.3 μT。实验测得的数据与标定值有一定的出入,主要原因是由于本文中的超磁致伸缩材料为片状结构,由于实验室的工艺原因,光纤耦合效率不高,造成了一定的损耗。另一方面由于被测磁场本身的变化,也给实验结果带来了一定的偏差。
3 存在问题及分析
首先,温度对传感器的影响有两个方面,一是改变光栅的布拉格波长,另一方面是改变干涉光的相位。
通过对式(1)进行求导,可得布拉格波长在温度变化下的相对移动量
(11)
同理,对F-P腔的相位ΦB=4πnh/λB进行求导,可得相位在温度变化下的相对变化
(12)
结合式(11),相位变化为零。综上,在外界温度的影响下,光栅的布拉格波长发生漂移,但布拉格处对应的干涉相位变化始终为零,干涉光谱发生的变化体现为光谱整体的移动但形状不发生改变。
其次,磁换能器在拉伸腔长时,也同时将啁啾光栅进行了拉伸。这种拉伸改变了光栅的2个特性:光栅周期和折射率。对于光栅周期的影响,文献[12]对此做了仿真,结果表明:光栅周期的改变对反射谱没有影响。对于折射率的影响,通过MATLAB软件对该影响进行仿真,在保证其他参数不变的情况下,将折射率调制深度分别设为0.000 1,0.000 2,0.000 3,0.000 4,0.000 5,所得结果如图6所示。
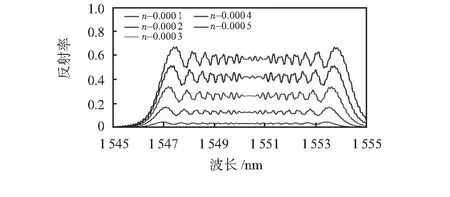
图6 折射率变化与反射谱的关系
结果表明,折射率的变化对反射谱有一定的影响。从图中可以推算出,光纤折射率每改变0.000 1,光谱移动大约0.1 nm,给系统带来的误差大约在3 %。
4 结 论
本文报道了一种基于全光纤啁啾光栅的宽带微型磁场传感器,分析了啁啾光栅F-P腔的传输特性并进行了数值仿真,采用条纹计数法对输出光谱进行解调,最后完成了对微弱磁场的测量。该磁场传感器具有体积小、响应速度快、响应带宽大、可多点组网等优势,在未来微弱磁场的测量中有着巨大的应用前景。
