MEMS振动陀螺仪AGC回路模型线性化与控制器设计

邢博文， 丁徐锴， 李宏生

(1.东南大学 仪器科学与工程学院，江苏 南京 210096；2.东南大学 微惯性仪表与先进导航技术教育部重点实验室，江苏 南京 210096)

0 引 言

硅微陀螺仪是一种非常重要的惯性传感器件，具有体积小、功耗低、成本低、易于批量生产等突出优点[1]。随着微机械加工工艺的发展，微机电系统(micro-electro-mechanical system,MEMS)陀螺仪在许多领域得到了广泛的应用，例如工业自动化、惯性导航和汽车电子等[2]。MEMS振动陀螺仪的一种常见的控制方法是自动增益控制(automatic gain control,AGC)。文献[3]采用自激振荡结合AGC的方式实现了陀螺数字化闭环驱动电路。文献[4]建立了非线性AGC系统模型，并通过相平面法和Routh-Hurwitz准则对整个回路的稳定性和收敛性进行了分析。文献[5]对自振荡驱动方法AGC环路进行了分析。大多数模型都能够预测AGC环路的稳定性，但很少能够直接指导闭环回路的设计。

本文提出了一种基于传递函数包络的AGC模型，并通过谐波分析方法对该模型进行了进一步的线性化。利用该线性化模型以及经典频域分析的方法可以很方便地进行控制器的设计。该线性模型使得控制器设计过程有了直接的指导并且使得仿真过程更加高效。

1 基于AGC的自激振荡驱动模型

MEMS振动陀螺仪驱动回路主要由硅敏感结构以及驱动和驱动检测电路组成。本文采用的陀螺结构为梳齿驱动结构，驱动电容器将加载到电容器极板的电压转换成静电力；驱动检测电容器将质量块的位移转变成电容的变化。忽略非理想因素，整个系统可以由图1和式(1)～式(5)进行描述[6]

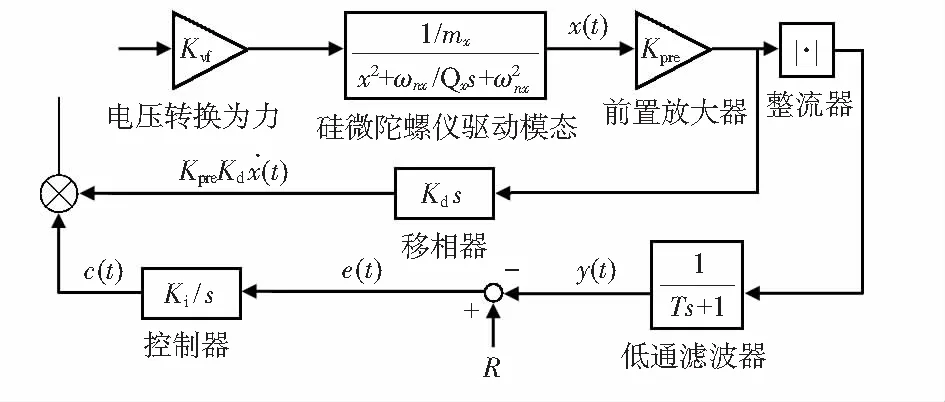
图1 自激振荡驱动回路框图

(1)

(2)

(3)

e=R-y

(4)

(5)

式中x为质量块沿驱动轴的位移，ωnx为驱动模态的固有频率，Qx为品质因数，f为驱动力，mx为驱动模态的有效质量，Kvf为电压转化为静电力的系数，Kpre，Kd，Ki以及T分别是前置放大器的放大倍数、移相器的增益、积分器的增益和低通滤波器的时间常数。

2 模型简化和线性化

2.1 模型简化

为了分析在一定驱动电压下位移包络的瞬态行为，假设

f(t)=p(t)·sinωdt

(6)

式中p(t)=P·u(t)，P为一个常数，u(t)为一个单位阶跃函数，移相器保证ωd=ωnx。将式(6)代入式(1)，考虑到Qx的值很大，所以，位移的包络可以近似化简为

(7)

则在驱动力的频率与谐振频率相同的前提下，驱动力振幅到驱动位移振幅的传递函数可以写为

(8)

在包络变化频率比信号频率慢得多的情况下，移相器输入输出信号包络之间的传递函数为KpsKdωnx。全波整流环节将信号的幅值以2/π的增益提取为一个与之相关的直流量。于是由一个纯积分器控制的AGC环路的自激振荡回路可以表示为方程(9)～式(11)，如图2所示。

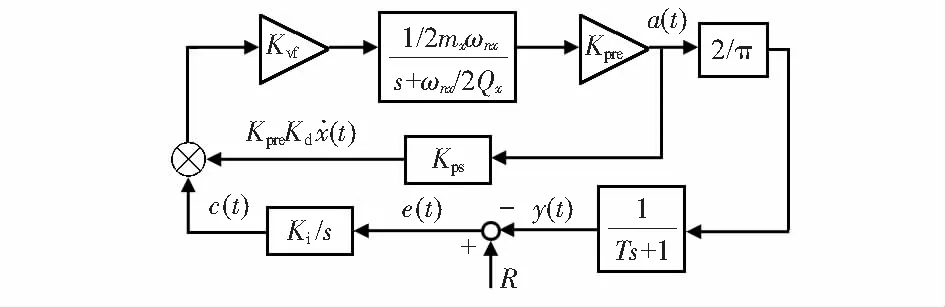
图2 简化的自激振荡驱动回路框图

(9)

(10)

(11)

式中K3为Kvf·Kpre·Kps,a(t)为位移x的包络。

2.2 模型线性化

简化后非线性系统的唯一平衡点可以通过令式(9)～式(11)右边全为零得到

在非线性系统平衡点附近的一个小邻域内，考虑非线性部分是在一个小周期信号驱动下的，则c(t)和a(t)可以表示为

c(t)=c0+Δc(t)

(12)

Δc(t)=Acos(ωt)

(13)

a(t)=a0+Δa(t)

(14)

(15)

将式(14)和式(15)两边对时间求导并代入式(9)可得

(16)

其中第一个式子反映幅频关系，第二个式子反映相频关系。

忽略高次谐波，可以得到

(17)

则从Δc(t)到Δa(t)的传递函数G(s)可以由式(17)和式(13)相比得到

(18)

通过将非线性的部分线性化，图2所示的模型简化为如图3所示。

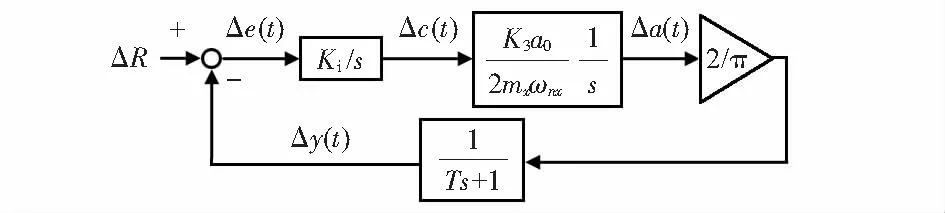
图3 驱动回路平衡点附近线性化框图

3 控制器设计

仿真中使用到的MEMS振动陀螺仪的物理参数：Kvf·Kpre/mx为27 140.6 N/V·m·kg，ωnx为20 664.2 rad/s，Qx为5 641，Kd为1.17×10-4，T为3×10-3s。

图3中描述的线性系统除了控制器之外的开环波特图如图4所示。由图可知，即使在非常低的频率范围内，系统的开环增益也很小，这意味着如果没有合适的控制器，稳态误差将会很大。因为稳态误差总是存在的，故引入一个积分器来提高系统的跟踪性能和抗干扰能力。但是纯粹的积分器会因其90°的相位延迟而使环路不稳定，故还需一个相位超前补偿环节以在增益穿越频率处获得足够的相位裕度。

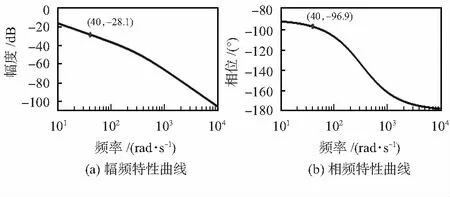
图4 不包含控制器的线性系统开环波特图

最简单的相位超前补偿的积分控制器的传递函数为

(19)

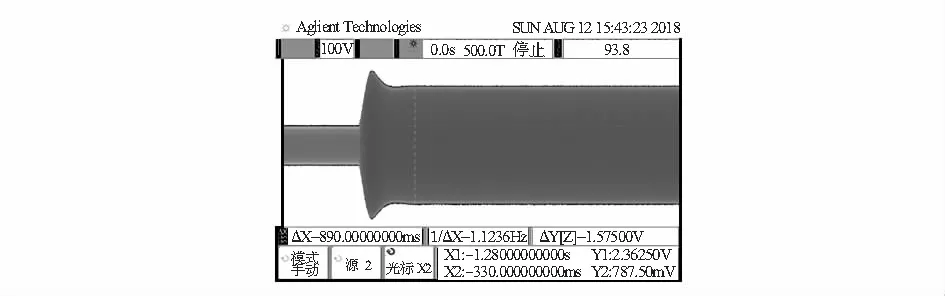
式中z为一个零点，p为一个极点，z

φc=arctan(ω/z)-arctan(ω/p)

(20)

对ω求导并令其为零，得最大超前角频率

(21)

将式(21)代入式(20)可以得到最大超前角

φcm=arctanλ-arctan(1/λ)

(22)

考虑到Kvf的有限性，增益穿越频率ωc可以根据经验设定在40 rad/s左右。较大的穿越频率通常意味着需要补偿更多的相位，这也是不切实际的。假设相位裕度不少于60°，且在该条件下闭环阶跃响应的超调是可以接受的，此时零极点对至少应该提供66.9°的相位超前，即λ=4.9。结合式(19)和式(21)，可以获得控制器的参数

Ki=4 945;z=8.2;p=195.2

(23)

图5是以式(23)为控制器参数的系统开环波特图。增益穿越频率、相位裕度和幅值裕度分别约为40 rad/s，60°和21.9 dB。

4 仿真与实验

4.1 仿 真

在MATLAB的SIMULINK仿真系统中分别建立图1所示的非线性控制系统模型以及图3所示线性化的控制系统模型，模型相关参数同第3章所述，控制器参数如式(23)所示。设定参考值R为0.5，系统运行稳定后将一个幅值为1的阶跃信号加载到参考信号处，线性化前后系统响应曲线分别在图6中示出。

从图6中可以看出，原始的非线性模阶跃响应的包络与线性化模型的阶跃响应曲线非常相近，尽管存在一些差异，但是线性化模型足以预测原系统的动态行为，即利用该线性模型进行控制器设计的方法是可行的。

4.2 实 验

为了进一步验证该线性化过程以及控制器设计方法的正确性，在平衡点处进行了阶跃响应实验。

实验用的陀螺仪是本课题组自主研制的全解耦双质量线振动硅微陀螺仪[8]，陀螺仪及其PCB电路如图7所示。

图7 真空封装陀螺仪及其驱动电路实物

控制电路的原理图在图1中示出，其中补偿控制器部分的电路如图8所示。

图8 补偿控制器电路

该部分电路的传递函数为

(24)

取

R=100 kΩ;C=2 nF;R1=600 kΩ;

R2=30 kΩ;C1=0.2 μF

(25)

则Ki=5 000;z=8.3;p=175，该组参数和式(23)给出的参数非常接近。

使陀螺在参考值R为0.5，控制器参数如式(25)所示的状态下工作，稳定后加载一个幅值为1的阶跃信号，系统的响应曲线如图9，可见AGC回路经过890 ms达到稳定，与图6中的仿真结果相一致。

图9 实际陀螺系统AGC回路平衡点处阶跃响应处阶跃响应

为了验证在该控制器控制下系统的环境适应性，分别进行了常温和全温测试。

将陀螺控制系统置于常温下，对位移信号振动幅度的稳定性进行测试，图10(a)，截掉前20 min，计算得振幅的标准差为8.5×10-3mV。振幅在前20 min内迅速上升了约0.2 mV，之后在1.115 32 V上下轻微波动。这里0.2 mV的下降主要是由非理想整流器的温度特性引入的。

在-40～60 ℃的全温范围内，对陀螺仪驱动回路的性能进行了测试[9]，结果如图10(b)所示。

图10 常温和全文下测试结果

由图10可以看到位移信号的振幅始终保持在一个相对稳定的范围内，在100℃的温度范围内变化约1 mV，计算可得全温范围内振幅的相对稳定性为9×10-6/℃。

5 结 论

本文针对MEMS振动陀螺仪驱动回路的AGC环路建立了其线性化的模型并利用该线性化模型进行了控制器的设计。在SIMULINK环境下进行了AGC环路的仿真，并设计了实际电路进行实验验证。实验结果表明:AGC环路平衡点出阶跃响应建立时间为890 ms，与仿真的860 ms基本一致；室温下截掉前20 min后振幅的标准差为8.5×10-3mV；全温度范围内，振幅相对稳定性为9×10-6/℃。因此，所提出的MEMS振动陀螺仪AGC回路线性化过程以及控制器的设计方法是有效的，且该控制器具备一定的环境适应性。