基于SURF特征的枪弹痕迹匹配方法*
2019-11-18李赵春殷旭阳
李赵春, 周 骏, 张 浩, 殷旭阳
(1.南京林业大学 机械电子工程学院,江苏 南京 210037;2.南京工业大学 机械与动力工程学院,江苏 南京 211800)
0 引 言
枪弹痕迹检验是指结合痕迹检验的一般方法以及枪械和弹道学的相关知识,对涉枪案件中的枪弹痕迹进行检验分析,为案件侦破提供线索、为刑事诉讼提供证据[1]。传统的弹痕检验方法主要是依靠弹痕检验人员,通过显微镜观察弹痕表面的细节实现子弹的比对。整个过程耗时长、工作量大且主观性强,不能满足枪弹痕迹快速、准确检验以及串并案的需要[2,3]。随着计算科学的发展,弹痕自动识别技术已经成为实现弹痕比对的有效途径。借助模式识别、数据挖掘等相关技术,提取和分析痕迹表面特征信息,可以准确高效地完成子弹和枪支的识别。
2017年,Chen Z等人[4]率先提出将CMC算法应用于弹底窝痕检验,给出了一套痕迹表面数据预处理方法如滤波、极端噪声和空值点剔除等,突出重点纹理信息,并通过对样本进行匹配元划分、旋转、互相关计算、匹配元一致性统计等处理,初步实现了枪弹痕迹的区域匹配与识别。本文则是从另一个角度出发,尝试将局部特征识别算法SURF应用于弹底窝痕匹配,以实现弹壳痕迹的快速高效比对。
1 SURF痕迹特征提取
SURF是一种基于尺度空间的局部特征提取和描述算法,源于SIFT算法的改进,主要应用于图像配准与识别[5,6]。算法使用积分图像并采用近似Hessian矩阵实现特征点检测;基于Harr小波分布生成特征点描述子,即特征点主方向分配和特征向量提取[7]。与SIFT相比,SURF除兼具鲁棒性、尺度不变和旋转不变性外,其运算量大幅减小,速度更快[8]。
如前所述,弹底窝痕是指弹壳底与弹底窝紧压贴合所留痕迹,表现为三维表面微观几何形貌,其表面波长成分可分为形状、波纹度和粗糙度。形状和波纹度通常反映了枪支的类特征,可用来识别枪支的种类,或枪支批次;粗糙度则包含了更多的个体信息,可以记录枪支部件在生产过程中表面的加工特点,具有唯一性,因此可被用来进行枪支鉴定。从实验看,粗糙表面的特征点更多表现在凸峰或凹谷,而实际的鉴定工作也基本围绕着这些较为突出的峰谷特征进行。SURF进行特征检测时所提取的特征点基本呈现斑点结构(blob-like structures),这些斑点结构恰恰就是凸峰或凹谷最基本的表现形式,因此,从理论上来说SURF对于纹理形貌的描述具有一定的适配性,可用于枪弹痕迹表面形貌的特征提取与匹配。
1.1 基于近似Hessian矩阵的特征点检测
使用Hessian矩阵来检测特征点,通过计算Hessian矩阵行列式局部最大值定位目标中的特征点[5]。SURF在构造尺度空间时,图像大小保持不变,通过逐步放大箱式滤波器对输入影像进行卷积操作得到尺度空间,然后在影像空间和相邻尺度的3×3×3的邻域内进行非极大值抑制,完成特征点的检测[6]。与尺度不变特征转换(scale invariant feature transform,SIFT)相比,箱式滤波器充分利用积分图像进行快速滤波,同时保留了更多的高频信息[9]。在弹底窝痕的三维表面形貌中,高频成分反映的是痕迹的粗糙度,涵盖了痕迹的绝大部分个体特征。图1为一弹底窝痕SURF特征提取结果,表现为特征点数量众多且分布均匀。
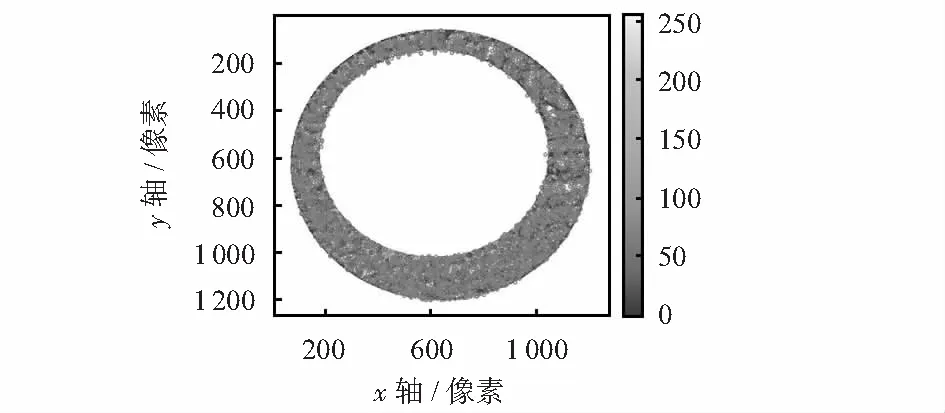
图1 弹底窝痕的SURF特征点提取
1.2 基于Harr小波响应的特征点描述子提取
SURF首先通过统计6s(s为特征点所在尺度)为半径的扇形窗口内x和y方向上的Harr小波响应来确定特征点的主方向,然后构造一个以特征点为中心、边长为20s、方向与主方向一致的正方形区域[9]。先划分为16(4×4)个子域,对每个子域分别统计x,y方向上的Harr小波响应及其绝对值之和:∑dx,∑dy,∑|dx|和∑|dy|,从而得到4×4×4共64维的方向向量作为特征描述子[10]。
1.3 特征点初匹配
在弹底窝痕的特征点匹配中,可利用描述子间的欧氏距离判定特征点对的匹配程度。首先,取待匹配图像a中的一个特征点Pn0,根据欧氏距离的大小找出对应另一幅图像b的最近邻特征点Pn1和次近邻特征点Pn2,然后计算这两个特征点与Pn0之间欧氏距离的比值K,当比值小于阈值时,则判定为特征点匹配
(1)
1.4 基于RANSAC提纯的误匹配点剔除
基于最近邻比值的方法只是实现了样本间的初匹配,如图2(a)所示,其中仍然存在较多误匹配点对,为此引入RANSAC对样本间匹配点对进行提纯。首先从初始匹配对中随机抽取几个匹配对,并建立一个符合匹配对的几何模型;然后把所有的初始匹配对代入模型进行评估,满足几何学模型的匹配对被采用为内点,不满足模型的为外点。整个过程:抽样,建模和评估都是重复的,当建立一个更好的模型的可能性变得足够低时,就终止该过程。RANSAC及其相关的假设验证方法在计算机视觉建模及匹配中得到广泛应用。提纯效果如图2(b)所示,经过RANSAC提纯后,匹配效果得到较大改善,所得匹配特征点对连接线基本平行。
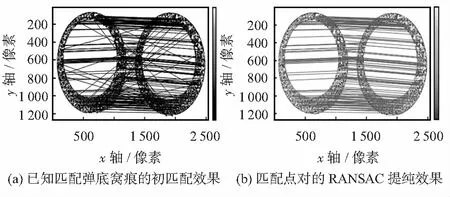
图2 经RANSAC提纯前后的匹配效果
2 SURF参数调整与选取
实验样本来源于美国国家标准与技术研究院(NIST)提供的弹痕数据库Fadul(2011)[11]。该数据库共包含40枚弹底窝痕,分别由10支手枪击发,枪支类型为9 mm口径Ruger P95。数据库样本采集均采用μSurf disk-scanning共聚焦显微镜完成,这种显微镜可以对三维表面形貌实现无损采集,该共聚焦显微镜具体的操作以及参数设置可参考具体文献[12]。
为了提升弹痕比对效率,满足刑侦过程中高速有效的弹痕检验需求,对SURF算法参数与枪弹痕迹匹配效果的关系进行了深度分析。SURF算法在特征点检测环节中可调整的参数[16]主要有组数(Octaves)、层数(OctaveLayers)和Hessian矩阵行列式阈值(Hessian-Threshold)。与SIFT算法类似,在构建尺度空间之后,需要将尺度空间划分为若干个组(Octaves)。一个组代表了逐步放大的滤波模板对同一输入图像进行滤波的一系列响应图。每个组又由若干固定的层(OctaveLayers)组成,层数控制着每组所使用的滤波器数量。其中组数和层数决定着箱式滤波模板的大小,即在哪些尺度空间中提取特征点。Hessian行列式响应图像表征图像中对应位置的特征强弱程度,根据特征的强弱,设定Hessian矩阵阈值,对特征点进行筛选,提取符合阈值的特征点,再对这些特征点进行描述。这三个主要参数的选取应结合样本的实际特点,综合考虑算法的效率、效果和稳定性[13]。
SURF算法中的参数设置对于不同的处理对象应有不同的取值策略,尤其是针对弹痕这类粗糙表面。本节重点讨论弹痕匹配策略中SURF最佳的参数取值方案。
2.1 组 数
以Fadul数据库中一对已知匹配样本为例(Fadul 7—1和Fadul 7—2),讨论改变组数对于匹配效果的影响,结果如表1所示(取矩阵阈值为3 000,层数为5)。
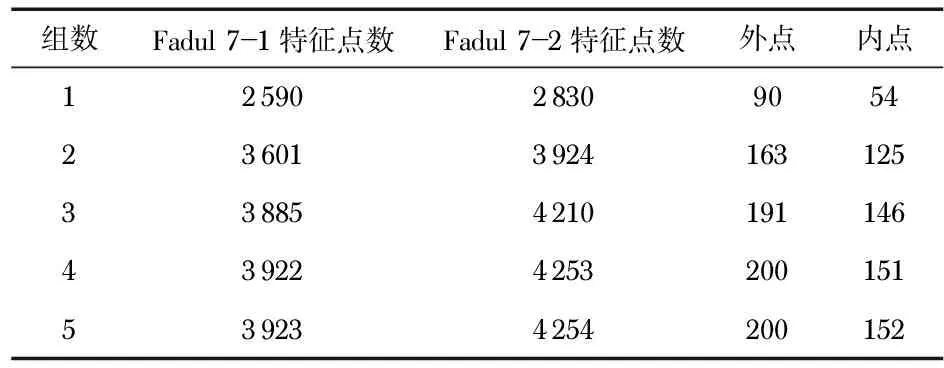
表1 Fadul 7—1与Fadul 7—2在不同组数下的匹配效果
组数量会影响检测到的特征斑点所覆盖的尺度空间的大小,组数量越大检测到的斑点越大。由表1可以看出,最佳的匹配效果组数取值在3~4之间,组数为3和组数为4匹配效果差别不大,而再取更大值时,效果几乎不变。
2.2 层 数
选择任意一对已知匹配的样本对(Fadul 9—1和Fadul 9—2),分析每组中的层数大小对于匹配效果的影响,结果如表2所示(其中取矩阵阈值为3 500,组数为4)。
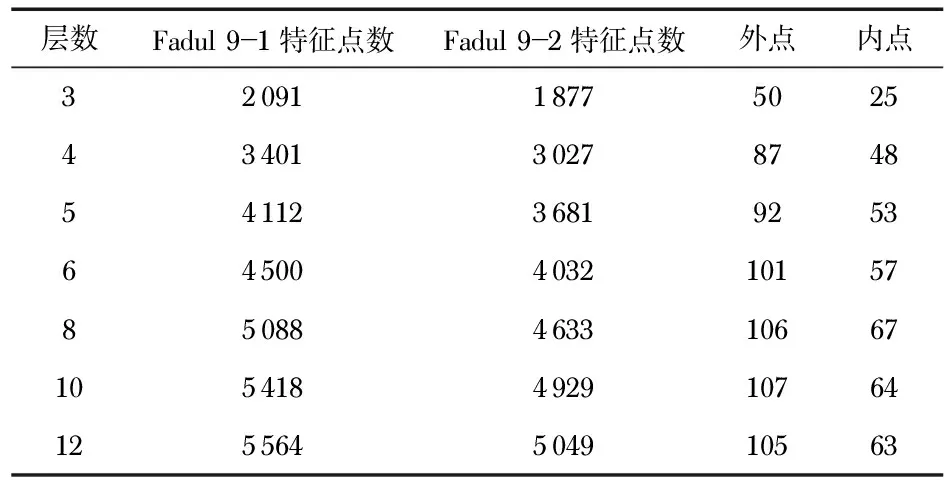
表2 Fadul 9—1与Fadul 9—2在不同层数下的匹配效果
由表2可以看出:层数对于匹配效果的影响很大,层数越大,匹配效果越好,但当层数的值超过8之后,整体的匹配效果变化不大,因此最终层数的取值选定在8~10之间。
2.3 Hessian矩阵阈值
如上节所述,层数在一定范围内增大可以改善匹配的效果,但通过实验发现,很多图像的匹配对出现在图像的空值区域,这是因为那些区域特征较弱的点以及图像的边缘点极易参与误匹配。可以通过设定阈值,将那些误匹配点剔除。再任取一对已知匹配样本对(Fadul 5—1和Fadul 5—2),改变矩阵阈值,其匹配效果如表3所示(取组数为4,层数为8)。
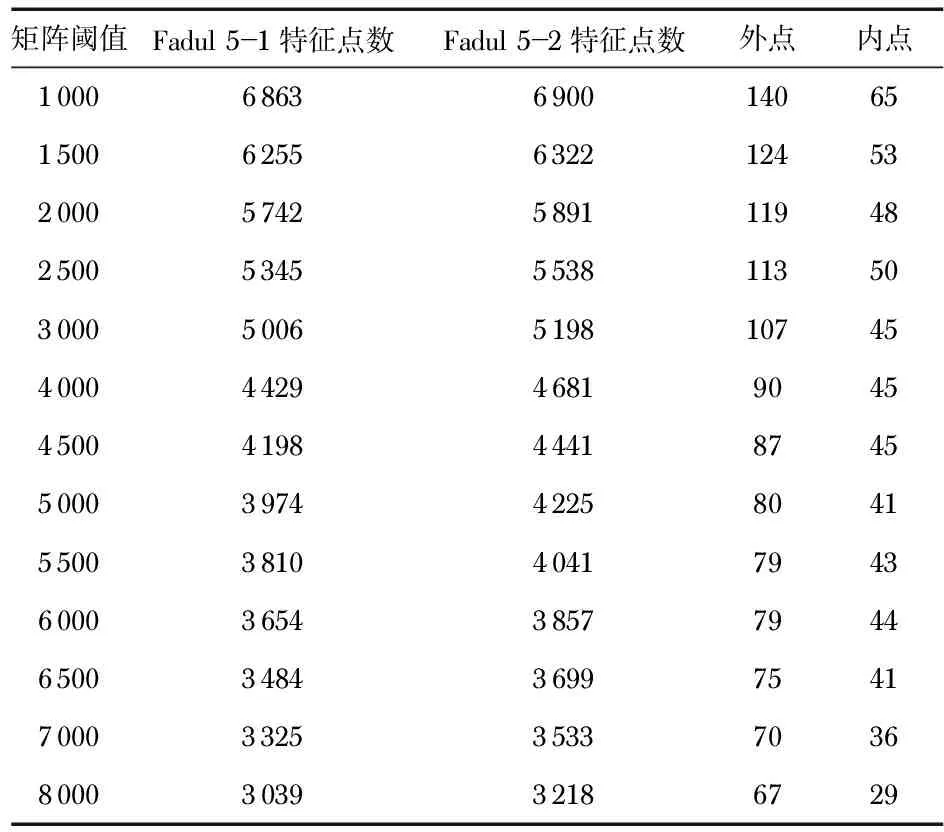
表3 Fadul 5—1和Fadul 5—2在不同矩阵阈值下的匹配效果
由表3可以看出,当Hessian矩阵阈值增大时,无效点可以被更有效地剔除,但是在一定程度上,也会误剔除部分有效的匹配对。所以需要根据尺度和组数选择适合的Hessian矩阵阈值,既要有效地去除误匹配对,又要最大程度地保留正确匹配对。根据10组样本的匹配效果来看,当阈值小于2 500时,保留了太多的无效匹配点;从3 000到6 500,匹配效果差距不大;当阈值大于6 500时,被剔除的有效匹配点变多,影响整体的匹配效果。因此,Hessian矩阵阈值合适的取值应该在3 000~6 500之间。
3 结 论
本文借鉴特征识别算法实现枪弹痕迹比对这一新思路,提出了基于SURF算法的枪弹痕迹特征检测、描述和匹配方法,并通过具体实验验证了该方法的高效性和稳定性。此外,重点讨论了SURF特征检测时参数设置对匹配效果的影响,并得到了以下结论:
1)将SURF应用于枪弹痕迹比对,可以实现表面纹理特征的有效描述,兼具旋转不变性和鲁棒性,其匹配效果良好。
2)通过详细实验论证可知,组数越大检测到的斑点越大,最佳的匹配效果组数取值应在3~4之间,当取更大值时,匹配效果几乎保持不变;层数对于匹配效果的影响较大,层数越大,匹配效果越好,其最佳取值应定于8~10之间;对于Hessian矩阵阈值,其值取3 000~6 500时,整体的匹配效果差别不大,取值更小或更大都会影响整体的匹配效果,因此,矩阵阈值的最佳取值应定于3 000~6 500,并视具体的样本以及组数与层数而定。
