小学生近似数量系统敏锐度与数学流畅性的关系研究

李烨 李蓉 邵秀巧

摘 要：近似数量系统是一种天生的理解和处理数量的能力。本研究探讨了近似数量系统敏锐度与数学流畅性之间的关系，使用非符号比较任务（Panamath）来测量近似数量系统敏锐度，数学流畅性主要是通过测试小学生1分钟内加减法和乘除法计算的正确率来获得。

关键词：小学生;近似数量系统敏锐度;数学流畅性

中图分类号：G420                       文献标识码：A                        文章编号：2095-624X（2019）29-0008-02

引 言

本研究发现，近似数量系统敏锐度与加减法计算的正确率紧密相关，而与乘除法运算的正确率无显著相关。近似数量系统敏锐度与数学流畅性之间的关系取决于数学计算的类型。

一、近似数量系统敏锐度对儿童数学能力的影响

近似数量系统是对数量的认知，新生儿和动物都具有这种能力[1]。它是个体在不依赖计算和数字符号的情况下，对一组非符号的数量进行近似表征的能力[2]。近似数量系统在数学能力的某些方面可能比其他方面更重要，因此，需要探索其与数学能力的具体衡量指标之间的关联[3]。目前，关于近似数量系统敏锐度与儿童数学能力的关系还没有一致的结论。一些研究认为，近似数量系统敏锐度与儿童数学能力呈现相关关系。近似数量系统敏锐度越高，个体的数学能力就越强[4]。近似数量系统敏锐度低的儿童在数学方面的表现较差，数学学习困难可能与儿童的近似数量系统受损有关[5]。近似数量系统敏锐度在预测儿童未来数学能力方面发挥着重要作用。3～4岁儿童的近似数量系统敏锐度可以准确预测他们6岁时的算术成绩[6]。但是，Inglis等（2011）发现被试对象的计算、加速计算、条件推理和应用问题的分数高低与近似数量系统的敏锐度无关。近似数量系统敏锐度与儿童数学能力之间的关系受多种因素的影响，其中数学流畅性可能是影响两者关系的重要因素，但目前还没有明确的研究结果。本研究旨在探讨近似数量系統敏锐度与数学流畅性之间的关系。

二、近似数量系统敏锐度和数学流畅性实验方法

1.被试对象

从河北省石家庄市某小学随机选取4～6年级90名小学生被试，每个年级30名学生，男、女生各半。

2.实验材料

本研究采用Panamath幻灯片来测量被试对象的近似数量系统的敏锐度。Panamath幻灯片一共有60张，每张幻灯片都由蓝色和黄色的点集组成。黄色和蓝色的点集同时在灰色背景下并排显示，每张幻灯片展示时间约1秒。每张幻灯片的黄色和蓝色圆点的结构、分组以及数量都是不同的。近似数量系统敏锐度使用韦伯分数（w）来描述。实验结束后将被试对象的成绩按照序列输入Panamath表格，计算得出w，从而测出被试对象的近似数量系统敏锐度。如果w越高，则近似数量系统的敏锐度越低。

数学流畅性通过加减法和乘除法计算的正确率来获得。实验中设置了两个测试，其中一个测试为132道加减法计算题，另一个测试为132道乘除法计算题。

3.实验程序

实验一共分两次进行。第一次是Panamath（近似数量系统敏锐度）和加减法测试。一周后是Panamath（近似数量系统敏锐度）和乘除法测试。

（1）近似数量系统敏锐度

整个测试分为练习阶段和正式测试两个阶段。

练习阶段。让被试对象先进行4个任务的练习，每张幻灯片呈现后，让被试对象展示出自己的答案，以便主试了解每个被试对象是否都理解实验任务。指导语如下：“你会在屏幕上看到一些蓝色和黄色的点，你需要去判断黄色和蓝色哪个点更多，这些点只会出现一小段时间。你不要数，用你的直觉来判断哪个颜色的点更多。”

正式测试。让被试对象在答题纸相应位置填写基本信息，包括姓名、性别、年级和日期。告知被试对象每一次试验中，需圈出“蓝色”或“黄色”，认为哪种颜色的点多就圈出相应的颜色;如果不确定，可以猜测，确保每次试验都有答案。每张幻灯片在屏幕上显示的时间非常短，所以被试对象很难在这么短的时间内数出数字。

整个实验进行集体施测，共需要5～10分钟。

（2）数学流畅性实验

在Panamath实验之后，被试对象要进行数学测试。第一次数学测试为加减法计算，第二次数学测试为乘除法计算。被试对象以书面形式回答问题，他们必须在1分钟内解决尽可能多的计算题。

4.数据处理

使用SPSS19.0和Panamath系统进行数据处理和分析。

三、实验测试结果

1.近似数量系统敏锐度

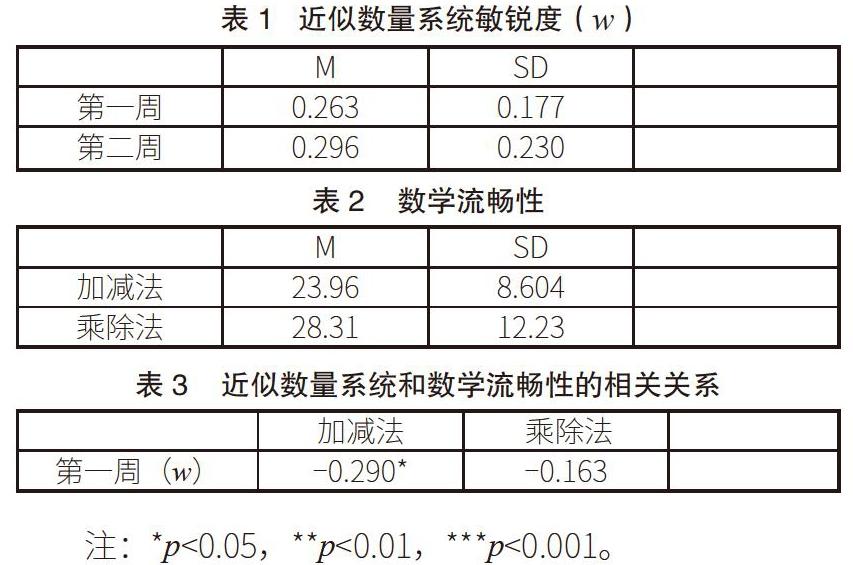
韦伯分数（w）越低表示近似数量系统敏锐度越高。从表1可以看出，第一周的w的平均分比第二周测试低，说明第一周的近似数量系统的敏锐度更高。为了提高评估测量的可靠性，计算了Pearson积差相关系数。第一周和第二周的韦伯分存在很强的正相关关系（r=0.482， p=0.001，<0.05）。Cronbach 's  alpha 为0.641（通常认为0.7到0.8为可接受值）。因此，之后数据中涉及近似数量系统敏锐度的分析使用的是第一周的分数。

2.数学流畅性

从表2可以看出，乘法和除法题中正确个数的均值高于加法和减法题中的均值（28.31>23.96）。被试对象在完成乘法和除法运算时表现较好。

3.近似数量系统和数学流畅性相关关系

表3说明，近似数量系统敏锐度与1分钟内加减法计算的正确率呈显著正相关关系（r=-0.290，p=0.033， <0.05），因为w低意味着高近似数量系统敏锐度。而近似数量系统敏锐度与1分钟内乘除法计算的正确率无显著相关。

四、近似数量系统敏锐度与数学流畅性关系的探讨

1.近似数量系统

实验第一周近似数量系统敏锐度要高于第二周实验，说明第一周的基础学习（数学学习和近似数量系统训练）对小学生的近似数量系统并没有起到太大的作用。但是，针对儿童的相关研究表明，持续的数学训练可以提高儿童的数学成绩。近似数量系统是否能通过训练而得到提高还有待进一步研究。

2.数学流畅性

加减法和乘除法是最基本的数学运算，人们从小开始学习计算，对于许多人来说，这几乎成了一个下意识的过程。加减法与乘除法相比，人们更倾向于用心算来解决加减法，而乘除法运算则可能借助九九乘法表或其他运算口诀来解决，也就是乘除法可能更依赖于记忆。由于乘除法计算依赖于熟练的口诀，因此，加减法的正确率要低于乘除法。这意味着解决加减法问题似乎取决于个人的数学能力。正确回答加减法题越多，越能反映数学能力的强弱。这也可能是影响近似数量系统敏锐度与数学能力之间关系的重要因素。

3.近似数量系统敏锐度与数学流畅性的关系

近似数量系统敏锐度与数学流畅性的关系取决于算术运算的类型（加、减、乘、除）。近似数量系统敏锐度与加减法计算正确率之间存在显著的正相关关系。这一发现支持了之前的研究，即在儿童中，近似数量系统敏锐度与数学能力有关，尤其是儿童算术运算。但是，近似数量系统敏锐度与乘除法运算无显著相关。这可能是因为进行乘除法运算时，人们更倾向于利用记忆力，而不是数学能力，这可能是导致近似数量系统与乘除法运算之间没有显著相关性的原因。

结 语

本文通过探讨近似数量系统的敏锐度与数学流畅性之间的关系，得出以下结论。（1）第一周近似数量系统敏锐度高于第二周，近似数量系统敏锐度是否可以通过相关的训练得到提高还有待进一步研究。（2）近似數量系统敏锐度与数学流畅性的关系取决于计算的类型。近似数量系统敏锐度与加减法计算正确率之间存在显著的正相关关系，而与乘除法计算无显著相关。数学流畅性可能是影响近似数量系统敏锐度与数学能力之间关系的重要因素。

[参考文献]

Brannon，E.M.，Jordan，K.E.，&Jones，S.M..Behavioral signatures of numerical discrimination.In M.L.Platt&A.A.Ghazanfar（Eds.），Primate neuroethology（pp.144–159）.Oxford：Oxford University Press，2010.

Piazza M，Facoetti A，Trussardi AN，Berteletti I，Conte S，et al..（2010）Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia.Cognition doi：10.1016/j.cognition.2010.03.012.

De Smedt，B.，No?l，M.P.，Gilmore，C.，&Ansari，D.How do symbolic and non-symbolic numerical magnitude processing skills relate to individual differences in children's mathematical skills？A review of evidence from brain and behavior.Trends in Neuroscience and Education，2013，2（2）：48-55.

Julie C.，G. Bel S. M.，Antonio V. S. P..Impact of High Mathematics Education on the Number Sense[J].PLoS ONE，2012，7（4）：832.

Libertus，M.E.，Feigenson，L.，&Halberda，J..Preschool acuity of the approximate number system correlates with school math ability.Developmental science，2011，14（6）：1292-1300.

Mazzocco，M.M.，Feigenson，L.，&Halberda，J..Impaired acuity of the approximate number system underlies mathematical learning disability（dyscalculia）.Child development，2011，82（4）：1224-1237.

作者简介：李烨（1988.7—），女，山西大同人，硕士研究生，讲师。

李蓉（1980.2—），女，河北石家庄人，本科学历，小学中级教师。

邵秀巧（1971.11—），河北石家庄人 ，博士研究生，副教授。