精于教学 准于设计*——以《分数的意义》课堂教学为例

吴善旺

一、立足课标 摸清学情

《孙子兵法》曰：“知己知彼，百战不殆。”教学亦如此，对于《分数的意义》这节课，笔者先认真研读课标，制订教学目标，根据目标制订相应的前测题目，运用电子书包统计功能，收集以下数据，并进行分析与处理。

例题1：下面各图的阴影部分能用分数1/3表示吗？如果能，请写出这个分数。

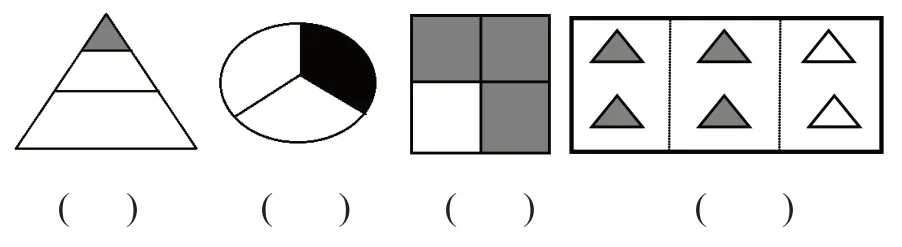
例题2：利用下图创造一个分数，并说说这个分数的意义

1.前测分析

学生在三年级上学期，对于初步认识分数掌握较好。但是对于分数必须是要平均分这个概念有些遗忘，对于单位“1”的理解上，大部分认为只能是一个物体。

参与前测的一共500人。具体结果见表1。

表1 前侧分析表

根据以上数据分析发现：学生已经初步建立了“分数”这个概念，能用分数表达生活中的事物。但并不是很明确分数的意义，对分数表示平均分没有很深刻的理解，观察、分析、概括能力不够强，“部分”与“整体”关系的了解不够多。

二、基于学情 精准设计

中医治病得先把脉，查清病因，方能对症下药，这一点在小学数学教学上也是类似的。福建省教研室主任罗明亮曾说过：“学生对于本节课知识大多数人都已经学会，您作为授课教师，是否依然涛声依旧？”学生已经会的，教师继续按照老套路教学，学生是否觉得厌烦？这样的课是否真的有意义？作为教师，更应该知道学生这节课还有哪个点是有疑问的。在《分数的意义》这节课中，根据前测中的问题，教学中有针对性地设计几个片段。

教学片段1：分数是先分后数的数，强调平均分。

例如，例题1中的三角形的阴影部分可以平均分吗？可以用分数表示吗？

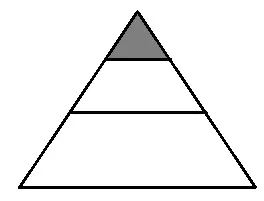
评析：解决前测中的不能平均分就不能用分数表示的问题，分数必须先平均分，才能得到分数。

教学片段2：探究以“一些物体”为单位“1”的分数表示法。

(1)操作探究

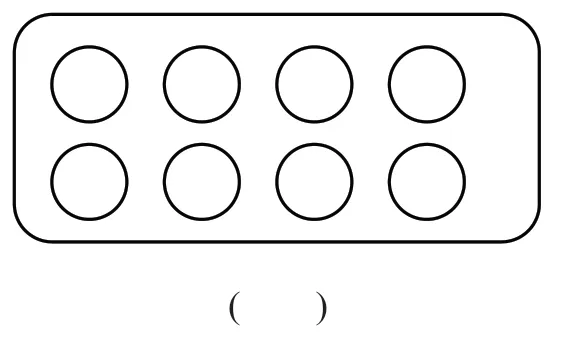
下面12个圆片，你能平均分吗？

在学习单上虚线画一画，并试着用分数表示其中的一份，比一比谁创造的分数多？

(2)展示交流

(你是平均分成几份？一份表示几分之几？两份呢？三份呢？)

学生可能平均分成2份、3份、4份、6份、12份5种分法。

追问：12个圆还可以怎么分？平均分成5份可以吗？7份呢？

引导小结：看来12个圆可以平均分成若干份，其中的一份或者几份都可以用分数表示。

分数的分母表示平均分的份数，分子表示其中的一份或若干份。

评析：在前测中发现大部分学生无法关注到平均分，所以降低难度，本环节先让学生尝试平均分，先找到平均分，然后再引导学生用分数表示，接下来拓宽学生思维，平均分成5份，7份可以吗？教师借助PowerPoint把12个圆叠加在一起，组成一个整体，形成一个圆柱状，利用PowerPoint动画演示切割过程。层层深入，打开学生的思维，平均分的份数不一定要是12的因数，任意整数都可以，所以就得到平均分成若干份。

三、巧用变式 突破难点

在日常教学中，教师应该熟读课程标准，明确重难点，练习的设计要紧扣重难点，但是不要出现大量的题目、复杂的题型，避免学生学习的负担太重。因此，巧用变式题组，增强学生的辨析能力，锻炼学生的思维，课堂上练习层层深入，让学生在课堂上的学习真正地发挥作用。以《分数的意义》为例，有以下例题供参考。

例1：把1米长的绳子，平均分成6段，每段是这条绳子的几分之几？

例2：把2米长的绳子，平均分成6段，每段是这条绳子的几分之几？

例3：把3米长的绳子，平均分成6段，每段是这条绳子的几分之几？

问题1：为什么绳子长度发生了变化，结果都是六分之一呢？

例4：把一条绳子，平均分成6段，每段是这条绳子的几分之几？

问题2：为什么不告诉你绳子长度，结果都是六分之一呢？

例5：把1米长的绳子，平均分成6段，每段绳子多少米？

例6：把2米长的绳子，平均分成6段，每段绳子多少米？

例7：把3米长的绳子，平均分成6段，每段绳子多少米？

问题3：观察例5，6，7题你发现了什么？

问题4：例1～4题与例5～7题有什么不一样？

评析：这1～7题，是小学数学的一个难点，也是高频考点，很多学生刚刚接触时对于这些题目是云里雾里。但是巧用变式题组，让学生在辨析中，理解分数的意义中的“量”与“率”的区别与联系，把复杂的数学问题简单化。

四、课堂后测 反思教学

有教师觉得，一节课上完，不知道学生接受知识程度如何，课余5分钟，笔者根据教学目标，设计对应的检测题，收集数据，既可以为这节课的教学效果反思，也可以为下一课的教学设计提供方向。同时也可以通过反思，为下一学年再教这节课积累宝贵经验。以《分数的意义》为例，部分题目如下。

例1：下面各图中都能用分数表示吗？能的请打√，不能的打×。

分析：本题3空的错误率分别为5%，1.25%，0。从数据看来，12个班级整体对于分数必须平均分已经掌握，对于多个物体表示分数也掌握得比较好。

例2：圈出每个图里表示的1/3。

分析：本题3图的错误率分别为：0，0，1%。从数据上看，学生对于《分数的意义》学习过程经历得不错，掌握较好，第2小题有5名学生答错，都是圈了3个桃子，受到思维定式的影响，而不是没有掌握知识点。

例3：填空题：

分析：第(1)题错误率为10%，第(2)题两空错误率分别为25%，38.75%。第(3)题两空错误率分别为：32%，10%。由此得出第(1)题掌握较好，剩下两道题，虽然经过变式题组比较，还是有很多学生答错，可见这个环节是一个难点，学生对于分数的意义从商的定义和分数与除法的关系上看，比较抽象，不好理解。后续还要进行适当的补充练习进行知识的巩固。

五、结语

精准化教学需要对教与学的过程进行数据的收集、分析，并将其融入信息技术支持下的教与学设计。教师不仅要关注学生是否掌握了知识、技能，更重要的是从学习的过程中得到的更加的客观、公正、精准的教与学评价，从而实现真正的有个性化的精准教学。未来，这种教学策略是时代发展的必然趋势，面对不同的学生，根据学生的学习习惯、生活习惯，会有一个智能的数据匹配，学生可以进行个性化的学习，教师可以更加精准化的教学。因此，这种精准化教学策略的研究，一定可以为未来的教育提升教学质量奠定基础，为未来学生减轻学习负担提供保障。