侵彻过程中弹头形状对PBX炸药损伤的影响*
2019-11-13石啸海余春祥戴开达崔云霄
石啸海,余春祥,戴开达,崔云霄,陈 华
(1 中国工程物理总体工程研究所, 四川绵阳 621000; 2 北京理工大学爆炸科学与技术国家重点实验室, 北京 100081; 3 西北核技术研究所, 西安 710024; 4 96901部队, 北京 100000)
0 引言
侵彻是指弹体在靶中的运动,是穿甲力学研究最关注的问题之一。弹体的侵彻行为与其头部形状密切相关,国内外研究者[1-3]对不同头部形状弹体侵彻靶体在侵彻性能、侵彻深度和侵彻过载等方面进行对比分析并取得了一些研究成果。但是目前关于弹体头部形状对装药损伤的影响研究还比较少。
内聚裂纹模型在Hillerborg[4]早期工作的基础上发展而来,基本理论框架是由西班牙马德里大学的Elice和Planas教授[5-7]基于强间断理论提出,可准确预测混凝土材料的断裂失效过程。内聚裂纹模型假设裂纹可发生在材料或结构的任何位置,引入能量方法来分析带预制裂纹或不带预制裂纹结构的断裂问题,后续得到不断的发展[8-10]。崔云霄等[11]改进了内聚裂纹模型,将其应用于PBX炸药断裂行为的模拟,并与试验结果进行比对。为准确预测PBX炸药在动载下的裂纹宽度和分布特征,文中采用了内聚裂纹模型模拟预测PBX炸药在侵彻过程中的断裂破坏行为。
1 内聚裂纹模型
内聚力模型(cohesive zone model,CZM)理论认为,裂纹尖端附近存在一个内聚力区,内聚力区的尺寸、内聚力的大小和分布与裂纹几何形状、外部载荷无关,其应力分布是该区域中材料点与裂纹尖端之间距离的函数,如式(1)所示:
(1)
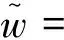
在载荷作用下,裂纹的行为一般包括裂纹的张开和滑移。内聚裂纹模型主要考虑裂纹的张开行为,将单元的位移场解耦为一个连续的位移场uα和一个间断位移场wα:
(2)
式中:Nα(x)为形函数,H(x)是Heaviside函数,A-和A+是裂纹张开时单元分离成的两个区域:
N+(x)定义为:
则相应的应变为:
εc(x)=εa(x)-[b+(x)⊗wα]s
(3)
其中:
在裂纹产生前,假设材料行为是线弹性的。裂纹起裂和裂纹方向采用最大主应力准则。一旦最大拉伸应力超过拉伸强度,材料开始起裂。假设裂纹的应力矢量与连续体中的应力矢量相一致,便得到内聚裂纹模型的基本方程:
(4)
式中:D是弹性模量的四阶张量。w是该方程唯一的未知变量,通过求解式(4),最终可得到单元应力。将内聚裂纹模型嵌入到LS-DYNA程序中,可以用于分析装药的动态损伤[11-12]。
2 有限元模型的建立
根据研究内容建立有限元模型,模型由弹体、装药、混凝土靶板组成。单元类型均采用SOLID164单元,利用六面体单元划分映射网格,靶板中心与弹体直接接触区域网格加密。为提高计算效率,考虑到模型的对称性,建立四分之一模型,对称面施加对称约束,共划分约20万个单元。混凝土靶板侧面和底部添加非反射界面。PBX炸药与弹体之间采用自动面面接触,弹体与混凝土靶板之间采用侵蚀面面接触。弹体直径为6 cm,装药长度为18 cm,壳体厚度为5 mm,混凝土靶板为Ф60 cm×80 cm的圆柱形,如图1所示。弹体正侵彻混凝土靶板,侵彻速度为600 m/s。
保持装药结构和弹体质量不变,改变弹头曲径比,建立几组模型进行计算,研究弹头曲径比1≤ψ≤4时装药的动态损伤。图2分别为ψ=1、ψ= 2.6、ψ=4的1/4缩比弹模型。

图1 四分之一弹靶模型
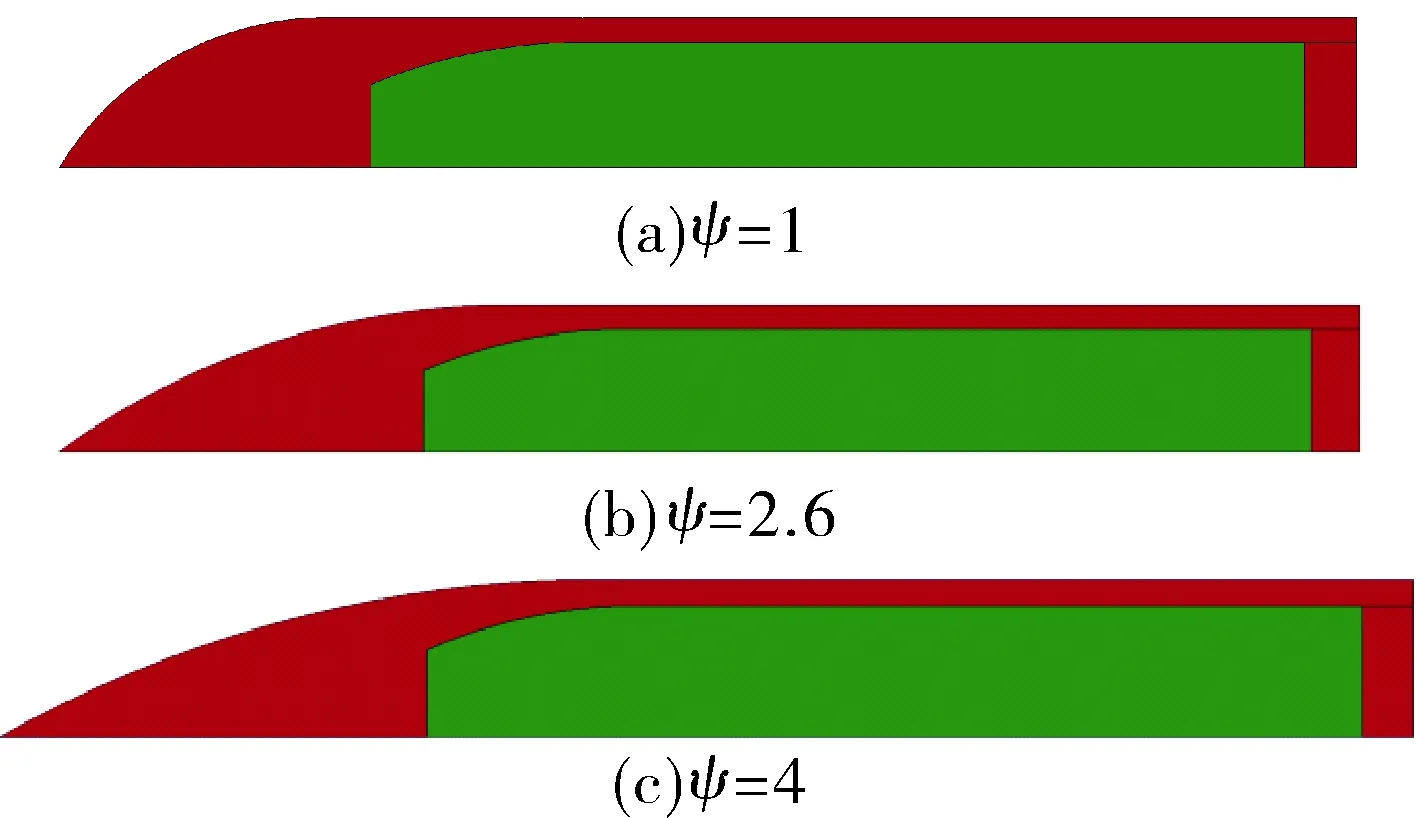
图2 不同曲径比的弹体模型
3 材料模型的选择
弹体为高强度钢,采用塑性随动硬化模型,屈服应力与应变率的关系为:
(5)

表1 弹体的材料参数
混凝土靶板采用HJC模型,该模型综合考虑了大变形高应变率下混凝土的力学响应。混凝土屈服强度用归一化等效应力来描述:
σ*=[A(1-D)+BP*N](1+C)lnε*
(6)
式中:σ*=σ/fc表示归一化等效应力(σ为等效应力,fc为准静态单轴抗压强度);A、B、C、N分别表示归一化内聚强度、归一化压力硬化系数、应变率系数和压力硬化指数;D(0≤D≤1.0)定义为损伤因子;P*表示归一化压力;ε*表示无量纲应变率。混凝土材料参数如表2所示。其中,EFmin为混凝土破碎的最小塑性应变;SAmax为混凝土所能达到的最大强度。
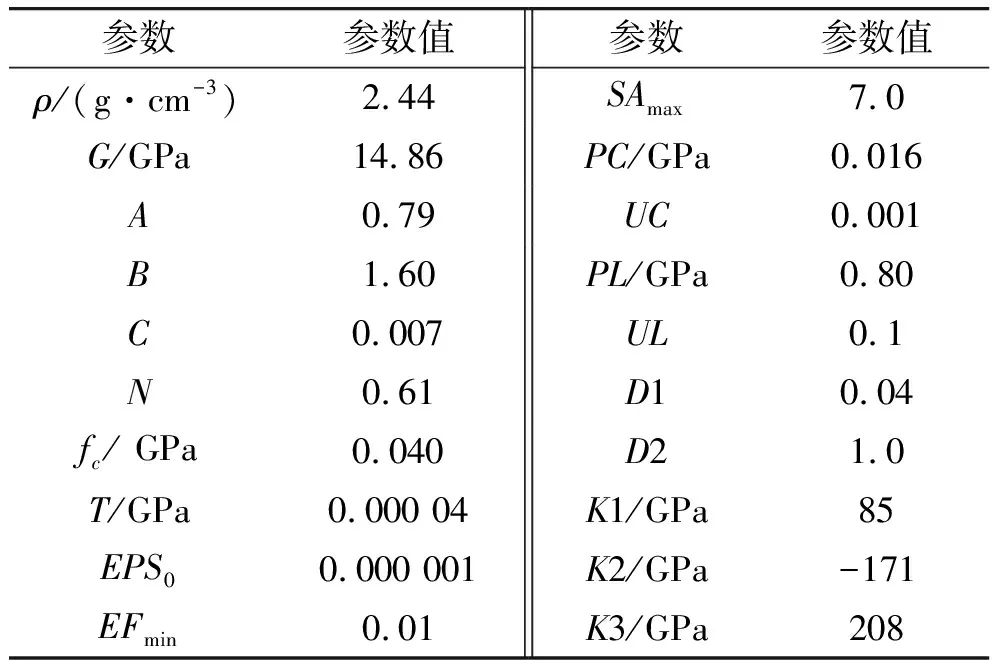
表2 混凝土靶板的材料参数
PBX炸药采用基于内聚裂纹的自定义材料模型,K和G分别为材料的体积模量和剪切模量,ft是材料的拉伸强度,Gf是材料的断裂能[12]。计算时没有考虑DIF增强效应,软化曲线选择线性软化形状。裂纹方向调整阈值和无量纲裂纹张开位移通过计算测试得到。该模型通过无量纲裂纹宽度ω表征装药损伤情况,单元裂纹宽度l与ω的关系为:
(7)
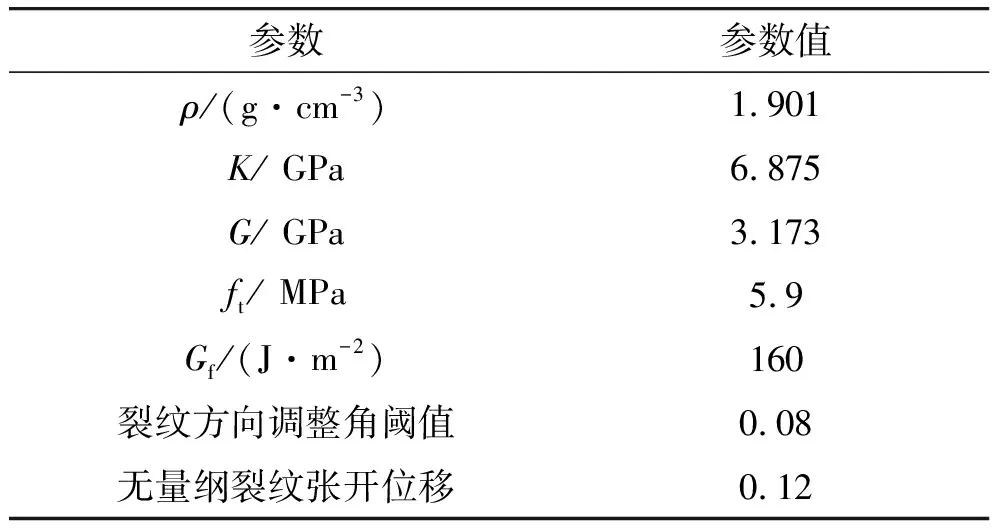
表3 PBX炸药的材料参数
4 计算结果及分析
4.1 初步计算分析
计算得到弹体和装药的过载曲线,如图3和图4所示。侵彻深度、侵彻时间和弹体最大过载的数据统计见表4。
不同曲径比下装药的最大过载都要大于弹体的过载峰值,这是由于弹体和装药之间的相对运动导致的。随着弹头曲径比增大,侵彻深度和侵彻时间增大,而弹体和装药的过载减小。
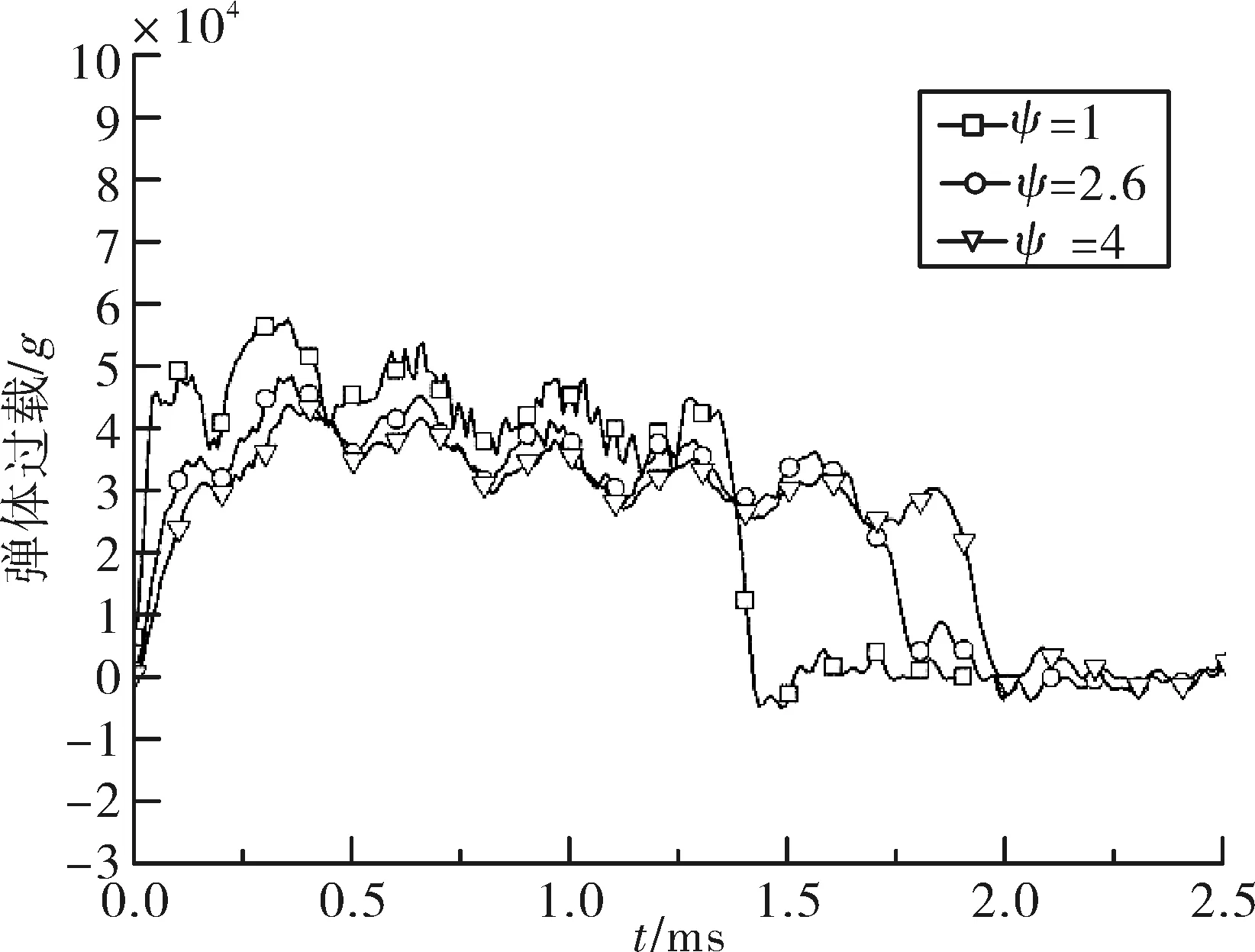
图3 弹体过载随时间变化
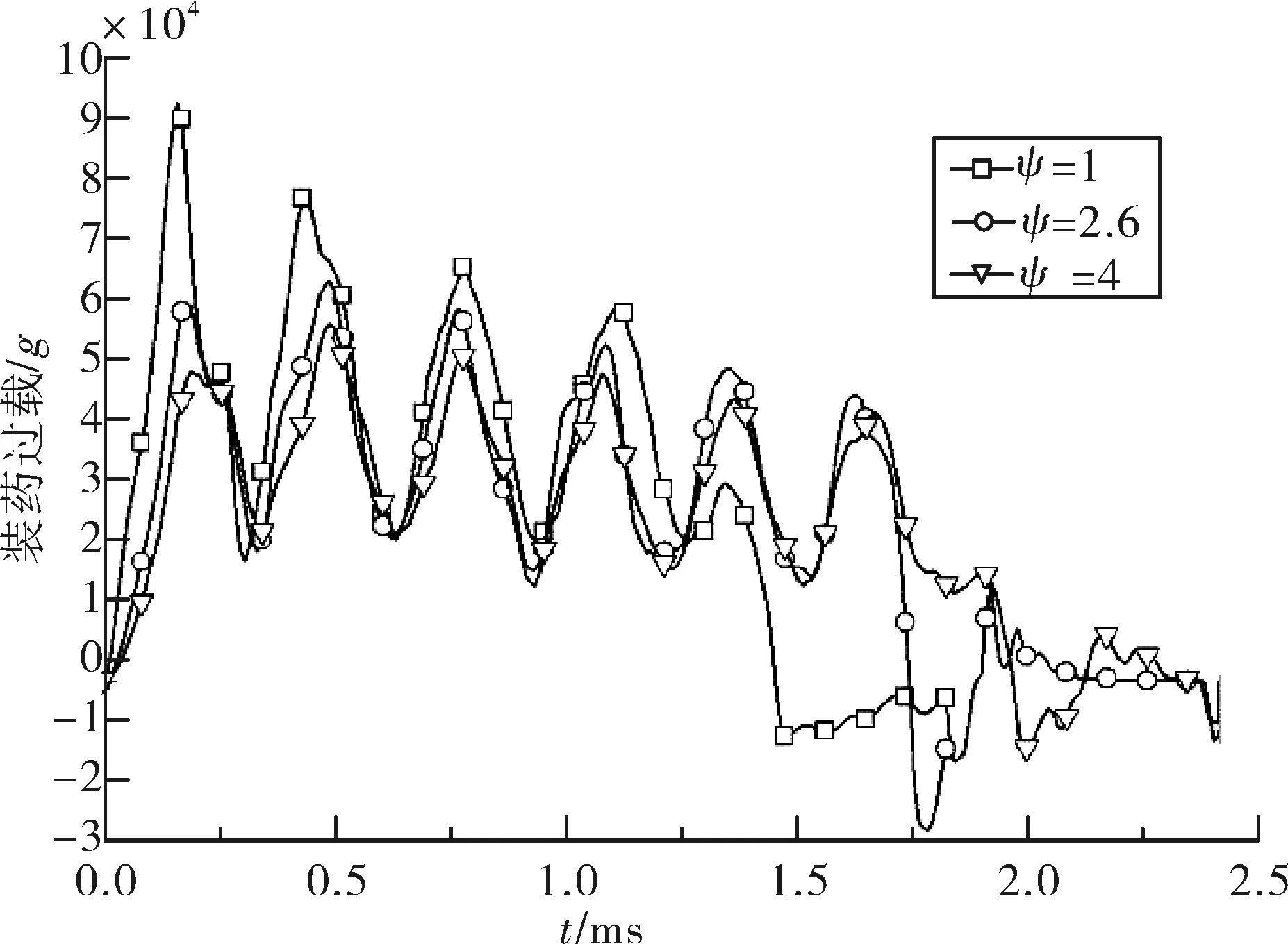
图4 装药过载随时间变化

弹头形状/ψ12.64侵彻深度/cm38.049.654.5侵彻时间/ms1.421.952.22弹体最大过载/g4.39×1044.85×1044.39×104装药最大过载/g9.05×1046.26×1045.60×104
图5为3种弹头形状的缩比弹侵彻结束时装药无量纲裂纹宽度ω的云图,表征装药的损伤情况。图5中单元的裂纹宽度由蓝色到红色逐渐增大。当ψ=1时,裂纹分布于装药各个部位,头部和尾部由于受到较大过载,受压产生严重损伤;中间部位受到拉应力和压应力的反复作用,裂纹横向扩展,形成断面。当ψ=2.6时,装药头部和中部仍有明显裂纹,而尾部装药几乎没有损伤。当ψ=4时,裂纹仅存在于头部和靠近尾部的位置,裂纹区域明显减少。
将图5中箭头指向处A、B、C的最大主应力与另外两个模型相应位置的最大主应力作比较。图6(a)表示3种弹体装药在A点的最大主应力,最大主应力在1.5ms之前没有太大差别,随后ψ=1和ψ=2.6的最大主应力值突然增大,对应图5中A点处ψ=1和ψ=2.6的装药都有裂纹存在。ψ=1的最大主应力最大值比ψ=2.6大,对应图6中ψ=1装药在A点处的裂纹宽度大于ψ=2.6装药的裂纹宽度。在图6(b)和(c)中也有这种现象。可以推测,单元最大主应力的突然增大,导致单元裂纹宽度急剧增大,形成裂纹。
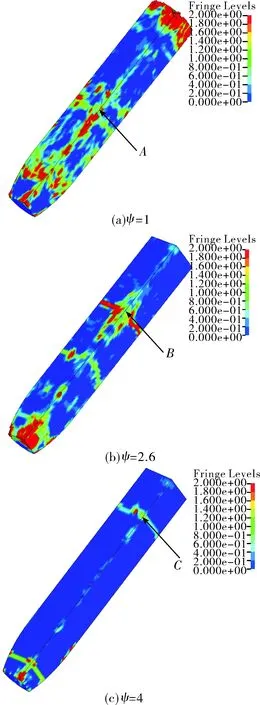
图5 装药的最终损伤情况示意图
图7为单元最大裂纹宽度随时间变化图。在0.4 ms之前,3种曲径比下的装药最大裂纹宽度增长趋势相似。随后ψ=1和ψ=2.6装药的单元最大裂纹宽度急剧增加,0.6 ms时ψ=1装药的单元最大裂纹宽度超过1.1 mm,1.25 ms时ψ=2.6装药的单元最大裂纹宽度超过1.1 mm。而ψ=4装药的裂纹宽度增长缓慢,最终最大裂纹宽度仅为0.62 mm。由于材料模型设置了单元删除阈值,当单元裂纹宽度超过1.1 mm时,该单元将会被删除,因此侵彻结束后ψ=1和ψ=2.6的装药最大裂纹宽度都超过了1.1 mm。
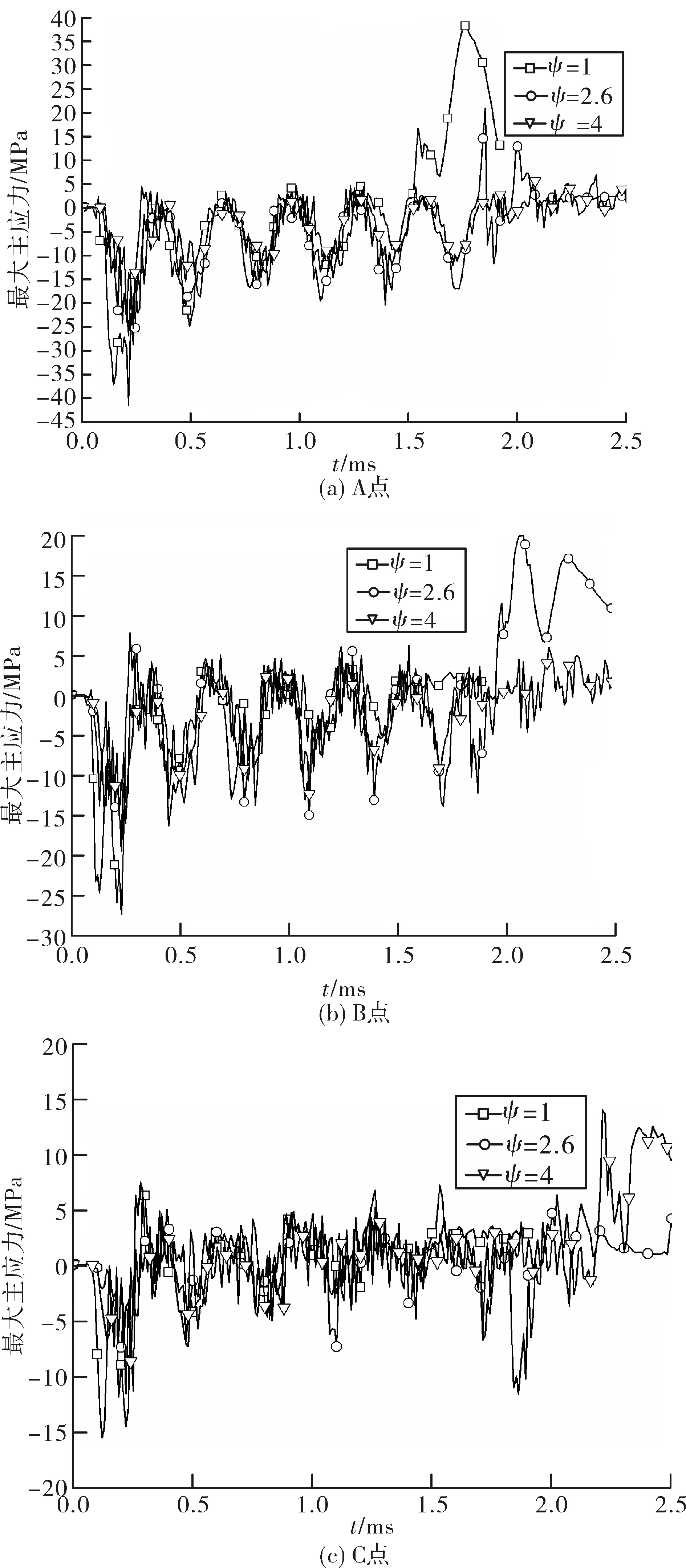
图6 装药最大主应力对比
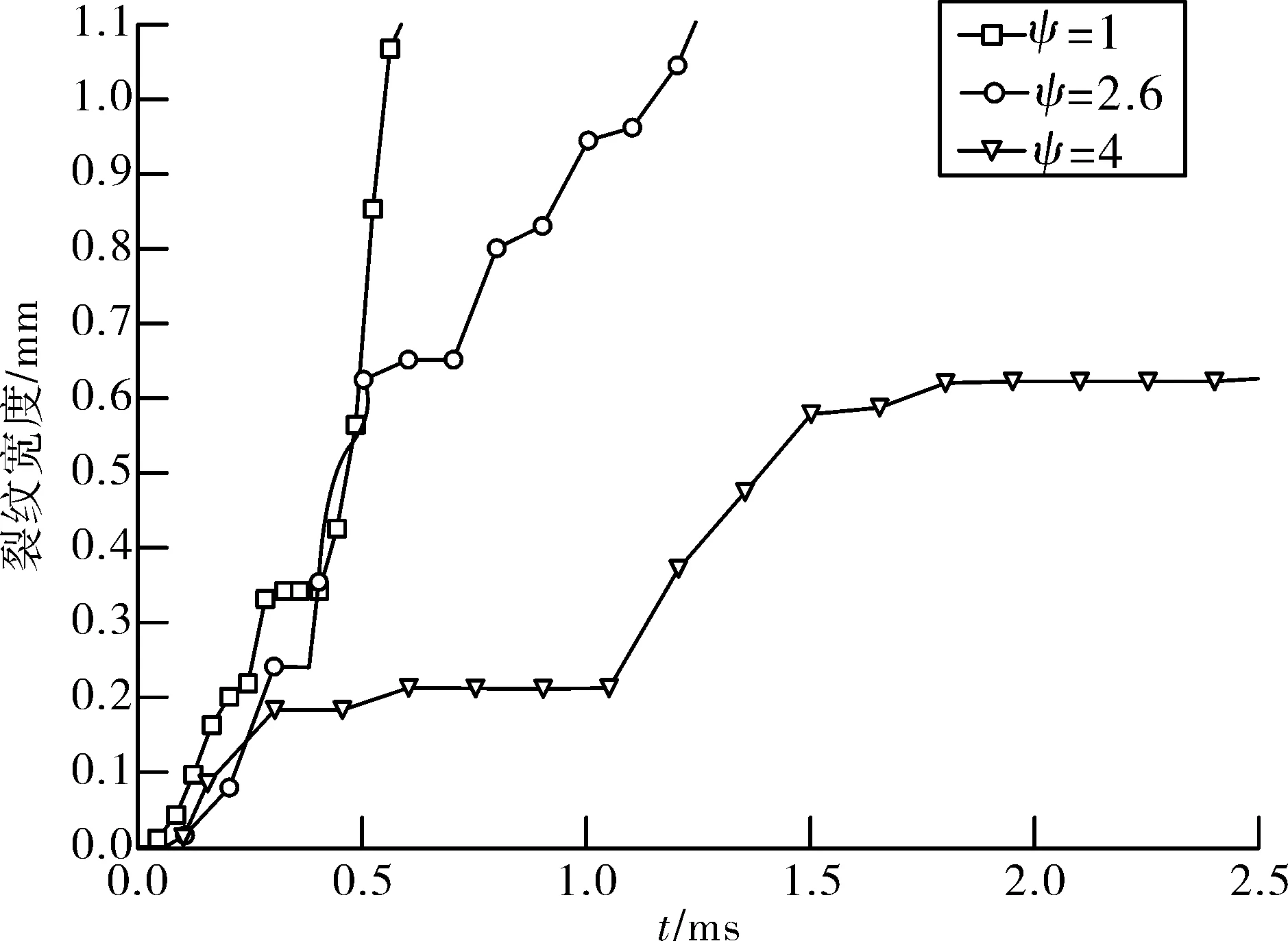
图7 最大裂纹宽度随时间变化
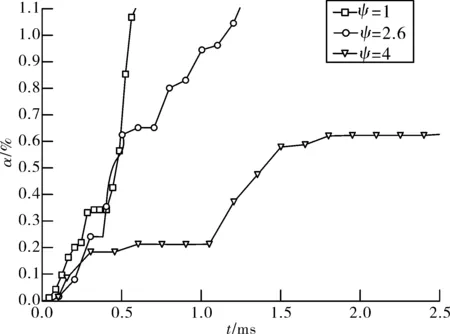
图8 可见裂纹含量随时间变化
将宽度超过0.1 mm的裂纹定义为可见裂纹,用α表示裂纹宽度超过0.1 mm的单元占装药的体积比,即可见裂纹含量。图8表示可见裂纹含量α随时间的变化情况。在侵彻过程中,ψ=1的装药可见裂纹持续增长;ψ=2.6的装药可见裂纹在2 ms之前增长缓慢,随后快速增长;ψ=4的装药可见裂纹增长速度最慢。3种弹头形状装药的最终可见裂纹含量αm分别为4.68%、1.47%和0.11%。
初步计算研究表明,弹头曲径比增加会使装药最大裂纹宽度减小,装药的可见裂纹含量也随之降低。
4.2 计算结果拟合
建立多组弹头曲径比在1~4之间的缩比弹模型并进行侵彻计算,得到装药过载和装药损伤等结果。对装药最大过载和弹头曲径比的关系进行拟合,如图9所示。可以看出,随着曲径比的增大,装药最大过载降低的趋势逐渐变缓。这种趋势与弹体最大过载随曲径比的变化趋势[13]相似。
图10为装药最终可见裂纹含量αm随弹头曲径比ψ增大的变化趋势曲线。从图中可以看出,曲线整体呈“减小-增大-再减小”的趋势。曲线在A区域时,αm随ψ的增大而减小,并在ψ≈2时达到极小值;当曲线在B区域时,αm随ψ的增大而略微增大;当曲线在C区域(ψ>2.4)时,αm随ψ的增大而减小,且减小趋势变缓。当ψ>3.5时,αm趋近于0。
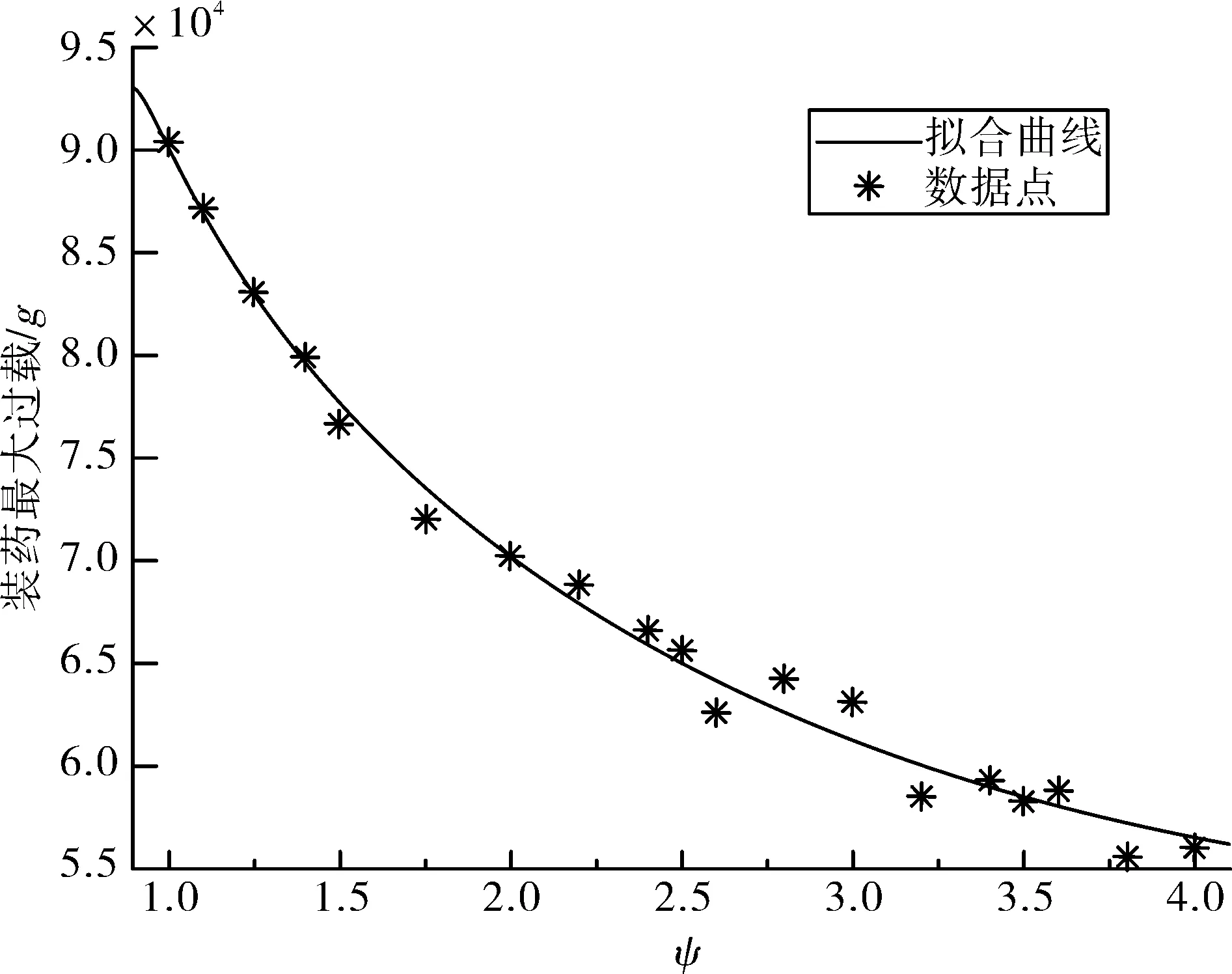
图9 装药最大过载与曲径比的关系
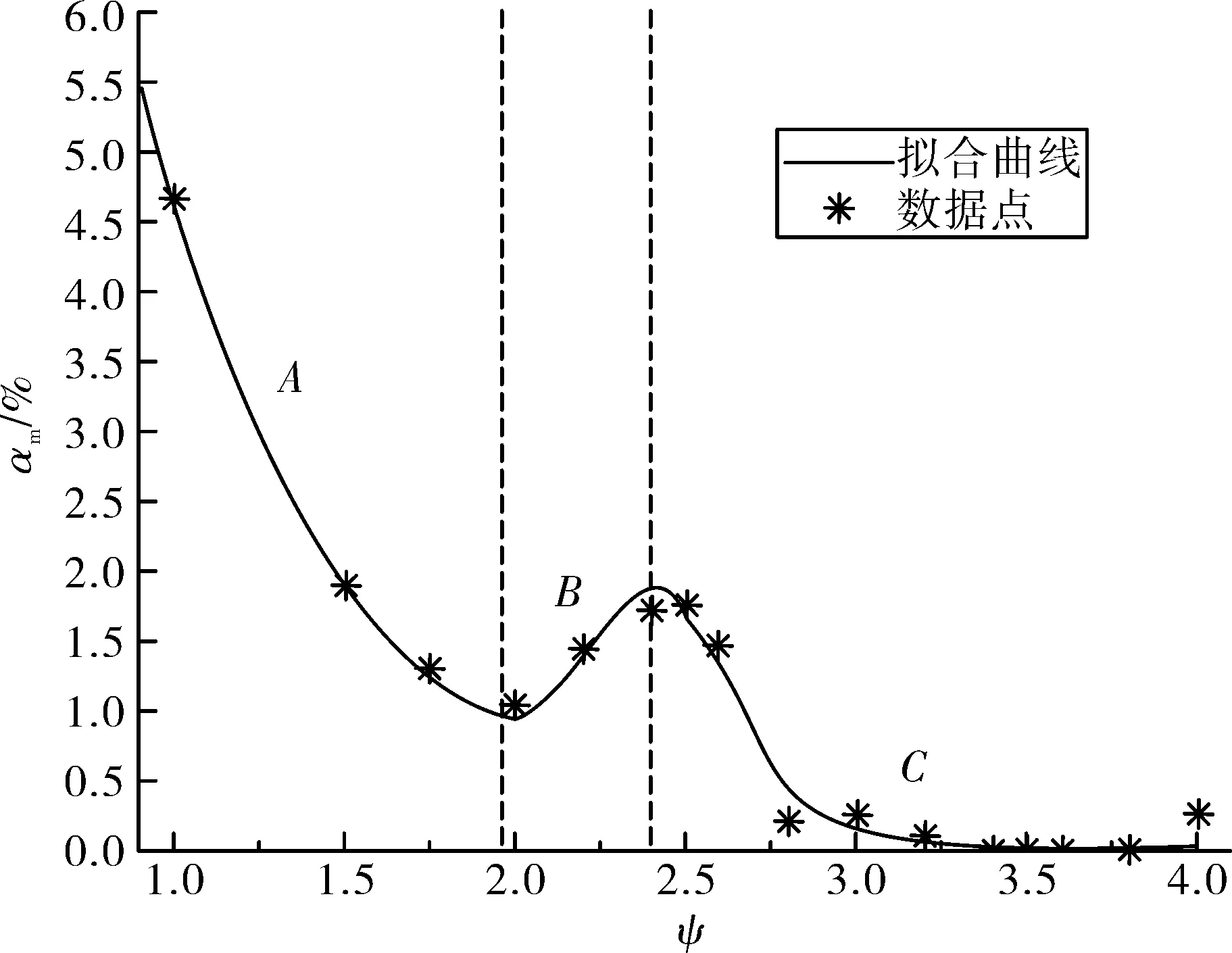
图10 装药最终可见裂纹含量与曲径比的关系
5 结论
利用LS-DYNA有限元软件,基于内聚裂纹模型,对某种缩比弹侵彻混凝土靶板进行了数值模拟。从过载、裂纹宽度、裂纹含量等角度比较了弹头形状对装药损伤的影响,得到如下结论:
1)弹头曲径比ψ增加会降低侵彻过程中装药的最大过载。随着ψ增大,最大过载值下降趋势平缓。
2)弹头曲径比ψ增加会使侵彻后装药最终可见裂纹含量出现整体下降,局部上升的趋势。
3)由内聚裂纹模型计算得到的装药可见裂纹含量,对工程设计具有一定指导意义。
