复合装甲材料厚度比对其抗侵彻性能影响研究*

吕竹文，吴 越，任 凯，刘玉军

(1 中北大学机电工程学院， 太原 030051； 2 山西聚脲防护材料有限公司， 太原 030006)

0 引言

现代战场复杂多变[1]，而穿甲弹的侵彻能力很强，是目前对主战坦克最具有威胁性的侵彻体之一。因此，多年来装甲设计者希望找到能够使穿甲弹侵彻能力降低的防护手段。目前，在装甲防护中采用较多的防护手段是在装甲表面增加其他结构，如反应装甲和复合装甲等。

为研究复合装甲材料厚度比对其抗侵彻性能的影响，基于ANSYS/LS-DYNA软件良好的性能及长杆弹穿甲理论，研究复合装甲三层材料厚度比对杆式穿甲弹侵彻性能的影响。

1 杆式穿甲弹侵彻厚度比为5∶3∶1的复合装甲数值模拟分析

陶瓷作为一种高硬度脆性材料，具有良好的抗侵彻作用，被广泛应用于复合装甲中[2]。文中的复合装甲，上层采用SiC陶瓷[3]，中间层为2024号铝，第三层为聚酰亚胺纤维。陶瓷材料发挥其高强度、高硬度作用，作为阻挡层；而铝合金的韧性好[4]、延展性好，声阻抗低(为1.69 kg·m-2·s-1)[5]，可以起到包裹破碎陶瓷的作用；聚酰亚胺纤维作为缓冲层，起到干扰穿甲弹、衰减应力波、防崩落、阻燃的作用。

1.1 杆式穿甲弹与复合装甲作用机理

通过建立复合装甲三层材料厚度比分别为1∶1∶1、3∶2∶1、5∶3∶1、6∶3∶1、7∶4∶1共5种抗穿甲弹侵彻有限元模型，详细分析三层材料厚度比为5∶3∶1的情况下，弹体头部磨蚀情况、质量损失及速度变化情况，得出结论可为优化复合装甲防护能力做出贡献。复合装甲的侵彻过程如图1所示。穿甲弹侵彻陶瓷阻挡层的第一阶段是破碎锥角的形成[6]，即t≤6hc/c；第二阶段为穿甲弹和破碎的陶瓷一起向前运动，继续侵彻，即t>6hc/c，其中hc、c分别为陶瓷的厚度和声速。

在第一阶段：

(1)

(2)

式中:Mp(t)、v分别为在t时刻穿甲弹的质量和速度，对于方程(1)和方程(2)，对给定的初始条件即可求出任意时刻的穿甲弹的质量和速度。由于在第一阶段作用时间很短，所以质量损失和速度损失可以表示为[7]：

式中:Mp1和V1分别为t=6hc/c时刻穿甲弹的质量和速度。

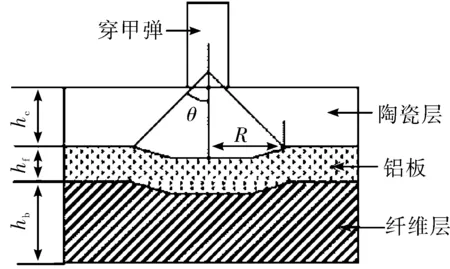
图1 弹靶作用简图

第二阶段，穿甲弹继续侵彻破碎的陶瓷锥角，后续的侵彻行为可以简化成穿甲弹和破碎陶瓷锥角共同侵彻剩余靶板。对于铝板部分，它被穿透所需的能量可以根据Martel假定来获得，其表达式为：

E2=πhfσsdD2/4

式中：hf为铝板的厚度；σsd为铝板的动态屈服应力；D为靶板的成坑直径，取D=1.8d。

穿甲弹侵彻尼龙材料的能量损耗为：

式中：εr为尼龙材料的最大破坏应变；σsf为尼龙材料的抗压强度；hb为尼龙的厚度；Mp1为第一阶段结束时穿甲弹的剩余质量；f(a)为：

式中mm为尼龙面密度。

利用能量守恒关系有：

从而可得陶瓷复合装甲阻挡穿甲弹的弹道极限速度表达式为：

杆式穿甲弹与陶瓷复合装甲作用机理是通过陶瓷板对弹体头部磨蚀[8-9]，因此对陶瓷的硬度具有较高要求，弹体在侵彻陶瓷板的过程中，会形成陶瓷锥，增大中间铝板层的受力面积，而铝板层因具有良好的韧性，可以包裹破碎的陶瓷继续与穿甲弹作用防止陶瓷破碎颗粒飞溅[10]。作为缓冲层，聚酰亚胺纤维会干扰穿甲弹，减弱应力波，防止崩塌和阻燃。

1.2 构建数值计算模型

文中的复合装甲上层为SiC陶瓷，中间层为2024铝，下层为聚酰亚胺纤维，总厚度为45 mm，三层材料厚度比为5∶3∶1。复合装甲与装甲钢靶板布置方式如图2所示，复合装甲放置角度为45°，穿甲弹直径d=22 mm，长径比为25[6-7]，以1 500 m/s的速度沿弹轴线侵彻复合装甲和装甲钢靶板。

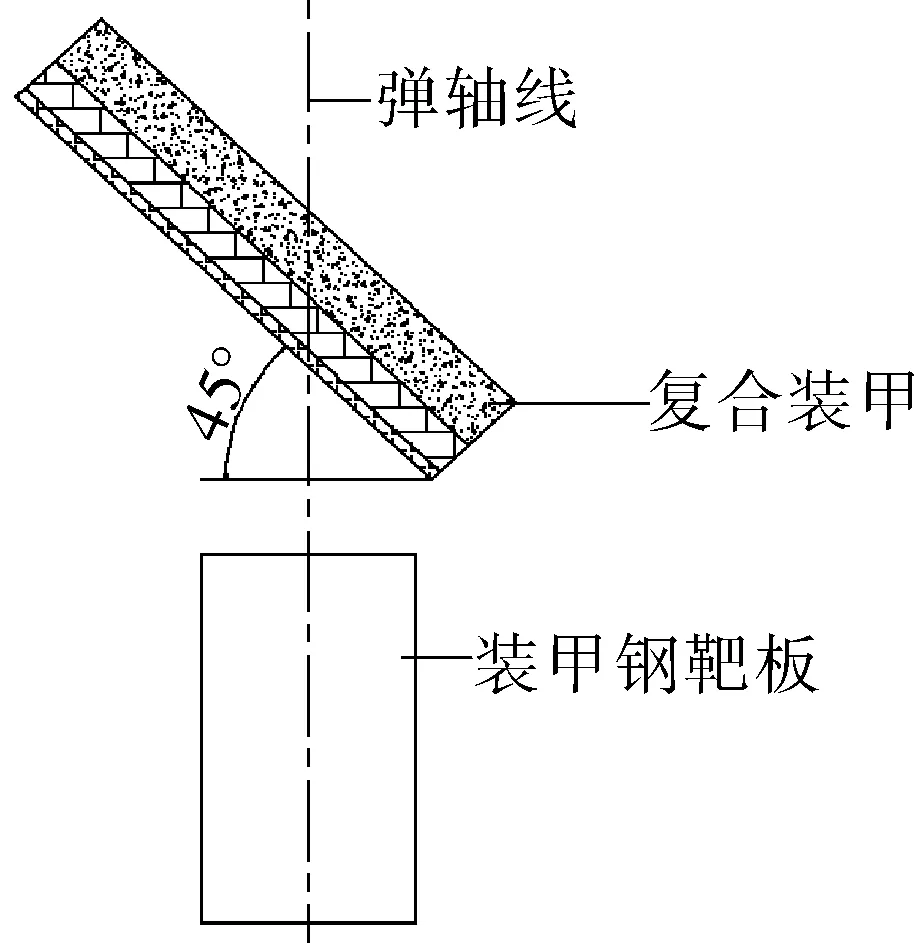
图2 厚度比为5∶3∶1复合装甲布置示意图

1.3 构建有限元模型

该有限元模型为轴对称结构，为方便计算，建立1/2模型。利用ANSYS/LS-DYNA进行三维建模，数值模型采用g·cm·μs单位制。有限元模型由穿甲弹、复合装甲、靶板几部分组成，均采用拉格朗日网格进行建模，见图3。文中所述穿甲弹模型为尾翼稳定脱壳穿甲弹(又称为长杆式穿甲弹)，其飞行弹体由风帽、弹体、尾翼等部件组成，为简化计算，文中有限元模型穿甲弹部分，只表现弹芯。穿甲弹材料选用93钨合金，靶板材料选用装甲钢，材料参数见表1。

图3 穿甲弹与厚度比为5∶3∶1复合装甲作用有限元模型

材料参数参数值材料参数参数值ρ/(g/cm3)7.85σY/GPa2.07E/GPa207β1.0υ0.3C/s-14.0Etan/GPa22P0.6

陶瓷材料模型选取Johnson-Holmquist(JH-2)陶瓷损伤模型。JH-2模型是由Johnson和Holmquist在JH-1[12]模型基础上发展起来的经验模型，主要用于陶瓷材料的工程设计。

金属材料应用最广泛的是Johnson-Cook模型和Mie-Gruneisen状态方程，文中采用这一模型。

聚酰亚胺纤维强度3.8 cN/dtex，伸长率32%，模量35 cN/dtex，密度1.41 g/cm，沸水和250 ℃收缩率各小于0.5%和1%。

2 数值模拟仿真结果分析

2.1 穿甲弹侵彻过程分析

当弹体以1 500 m/s的速度冲击复合装甲、装甲钢靶板模型时，弹体与复合装甲、装甲钢靶板变形发展过程如图4所示。

图3的数值模型中，复合装甲各层材料的厚度比为5∶3∶1，复合装甲总厚度为45 mm，陶瓷板的厚度为25 mm。当弹体以较高初速侵彻复合装甲时，在t=42 μs时，弹体头部已出现明显的破碎分离状态，头部顶端分裂成为两部分，在t=52 μs时，分裂状态更加明显，分裂尖端部分已出现破碎向外飞溅现象，随着侵彻过程的进行，弹体头部出现分裂，拉长飞溅现象，在图4(f)中最为明显，弹体头部尖端已出现明显的分离、破碎。在弹体侵彻复合装甲的过程中，弹体侵彻陶瓷板所用时间最长，头部磨蚀程度也最高，陶瓷板只在弹体侵彻孔径周围出现裂纹和孔洞，内部并未出现明显破碎和开孔现象，从图4(e)中可以看出；从图4(c)和图4(d)中可以看出，弹体侵彻铝板过程中，一直在冲击、挤压铝板，但铝板先是拉长、变形，给弹体一反作用力，最终超过材料自身断裂强度极限才出现开孔；在本节的数值模型中，聚酰亚胺纤维的厚度只有5 mm，但它起到了包裹弹体已经破碎的头部和弹体破碎的部分的作用。

图4 穿甲弹侵彻厚度比为5∶3∶1复合装甲发展过程图

2.2 弹头变形过程分析

从图5(a)中可以看出，弹体头部变形的过程，先是弹体头部尖端弯曲，在t=26 μs时，头部所受应力增大，出现镦粗、卷曲、变形，93钨合金的硬度很高，穿甲弹弹体头部尖端具有很高的侵彻性能，因此在复合装甲抗侵彻的过程中，使弹体头部弯曲、镦粗、卷曲、变形，可以有效降低穿甲弹的侵彻性能。在图5(c)中，弹体头部已弯曲的部分，由于反作用力的持续作用，出现孔洞，并在后续侵彻过程中，弯曲部分体积、质量继续增加，已弯曲的部分的孔洞直径继续增大，最后断裂分离、崩落、脱离弹体，此时弹体的头部部分尖端已不再明显，由于材料本身延展性良好，弯曲部分继续拉长，已经弯曲、拉长的部分对靶板的侵彻能力明显降低，在t=108 μs时，弹体所受应力明显增大，出现头部内部应力明显大于弹体后端的现象，受力不均会增大弹体的变形。

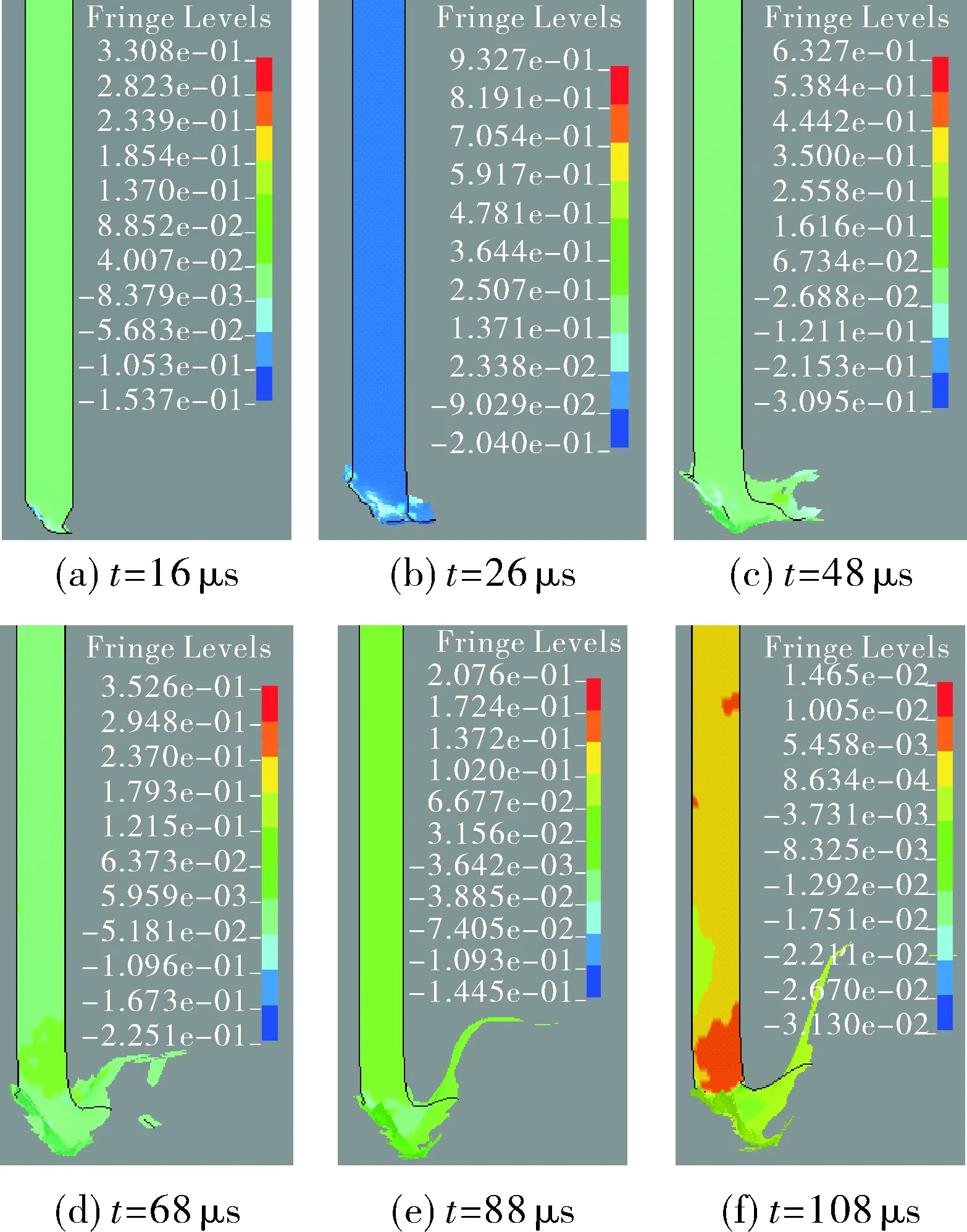
图5 穿甲弹头部变形过程

表2为穿甲弹穿透复合装甲所用时间及弹体长度、体积损失。从表2中可以看出，复合装甲可有效使弹体质量损失增加、长度降低。弹体头部具有较强的侵彻能力，而复合装甲正是与弹体头部作用，可有效降低其侵彻性能。

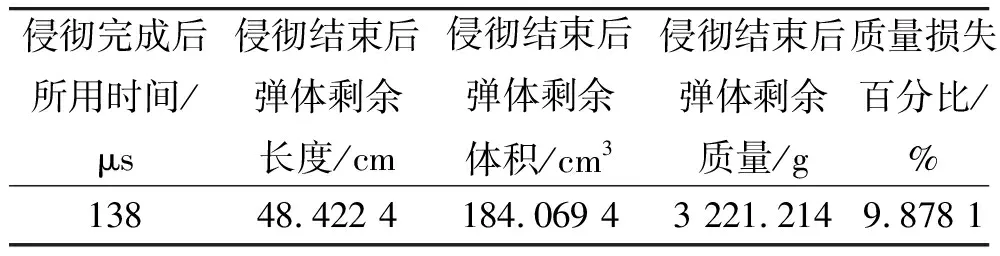
表2 穿甲弹侵彻厚度比为5∶3∶1时复合装甲

从表3可以看出厚度比为5∶3∶1的复合装甲，使弹体初速降低了25.87%。在复合装甲中，增加陶瓷板厚度，对降低弹体侵彻速度有明显效果，弹体初速被降低，侵彻性能随之降低。

表3 侵彻前后穿甲弹体速度变化对比

2.3 多种比例对比分析

由于篇幅限制，文中只详细介绍了三层材料厚度比为5∶3∶1的数值模拟仿真，为得出一般性规律，又进行三层材料比例分别为1∶1∶1、3∶2∶1、6∶3∶1和7∶4∶1的数值模拟仿真，对靶板侵彻孔径深度进行对比分析，如图6所示。

图6 3种材料不同厚度比例侵彻深度

图6中横轴上的0～4点分别表示比例为1∶1∶1、3∶2∶1、5∶3∶1、6∶3∶1和7∶4∶1，从图中可以看出，当比例为1∶1∶1时，靶板侵彻孔径深度最大，随着三层材料厚度比不同，侵彻孔径深度逐渐减小，在比例为5∶3∶1后，侵彻孔径深度下降趋势趋于平缓，综合考虑三层材料的每一层厚度和性能，建议采用三层材料厚度比为5∶3∶1。

3 穿甲弹威力计算

穿甲弹因初速高，动能大来毁伤钢甲[13]。而普通旋转式穿甲弹，因自身重量大，初速低，比动能小，所以其穿甲威力较小。目前这种结构已逐渐被淘汰，代之以脱壳穿甲弹。杆式穿甲弹的长细比大，比动能大，穿甲效能高。新设计的穿甲弹多采用这种结构形式。本节主要介绍杆式穿甲弹威力的计算，主要是从理论上验证数值模拟仿真的可行性。

当今，欧洲、美国大多采用穿甲弹击穿三层间隔装甲钢靶作为考核其穿甲性能的一种手段[14]。随着装甲技术的发展，最近这种方法，在我国也有所应用，并以此作为考核穿甲弹的性能指标之一。

据此，下面所介绍的方法，主要用于估算长杆弹丸穿透第一、第二两层靶厚的剩余质量mr和剩余速度vr，以便与弹丸残体对第三层靶作用的极限穿透速度vj估算值进行比较，从而判断弹丸穿透三层靶的可能性。

文中所述的数值模拟，已知93钨合金长杆形弹丸的下列数据：

弹丸质量m=3.574 kg；弹丸直径d=22 mm=0.022 m；撞击速度v=1 500 m/s；着角α=80°；弹丸材料的强度极限σb=1.275×109Pa；弹丸材料的屈服极限σ0.2=1.029×109Pa；弹丸材料的延伸率δ=4%；弹丸材料的密度ρp=17.5×103kg/m3。

靶板系统的数据(厚度mm/“牌号”)为：第一层：15/“2Π”；第二层：15/“2Π”；第三层：15/“2Π”。

靶板材料密度ρt=7.85×103kg/m3。

弹丸对三层间隔靶的穿透能力计算步骤及计算结果如表4所示。其中b为靶厚(mm)；ρ为靶塞密度(kg/m3)；Cm为弹丸相对质量(kg/m3)；Ce为靶板相对厚离；vj为极限穿透速度(m/s)；K为穿甲复合系数；σst为靶板材料的流动极限(Pa)；β为弹丸穿甲过程中的转角((°))；mq为靶塞质量(kg)；vr为弹丸穿透装甲后的剩余速度(m/s)；vf为弹体减速阶段后速度(m/s)；Cp为弹丸材料内的塑性波波速(m/s)；tp为冲塞过程的延续时间(s);Δm为弹丸在穿甲过程中的质量损失(kg)；ms为穿甲后剩余质量(kg)；αj为穿甲后的靶板着角((°))。

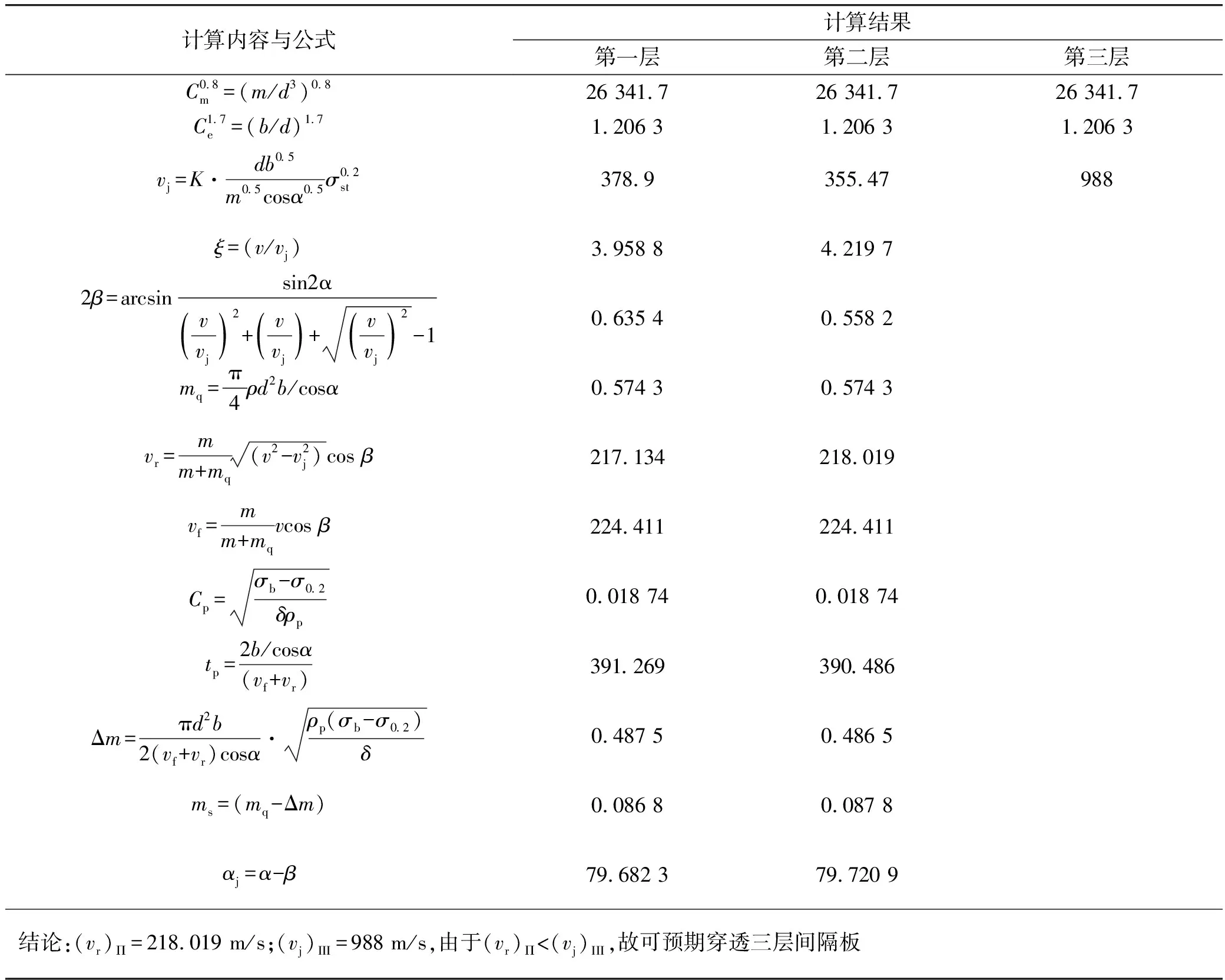
表4 弹丸对三层间隔靶的穿透能力计算结果

在所述的5种数值模拟中，弹体均穿透复合装甲，并穿透装甲钢靶板；在进行理论计算时，把复合装甲视为第一、二层靶板，下置装甲钢靶板为第三层靶板，理论计算结果：由于(vr)Π<(vj)III，故可预期穿透三层间隔板，数值计算结果与理论计算结果一致，故数值模拟计算可以为穿甲弹与复合装甲、装甲钢靶板相互作用过程提供一定的参考。

4 结论

文中分别介绍了碳化硅陶瓷、2024铝和聚酰亚胺纤维3种材料作为复合装甲材料的良好特性，从理论上分析杆式穿甲弹与复合装甲作用的机理，并进行多组复合装甲三层材料厚度比不同的抗侵彻数值模拟分析，得出：弹体初速为1 500 m/s，在复合装甲总厚度一定时，三层材料厚度比为5∶3∶1的复合装甲抗侵彻性能最好，使弹体质量损失9.878 1%、弹体初速降低25.87%，并使弹体偏离弹轴线，有效阻碍弹体侵彻复合装甲下置的装甲钢后效靶板。为验证数值模拟仿真的可行性，并进行理论计算，与数值模拟仿真结果进行对比，结果表明：数值模拟仿真结果与理论计算结果一致，可以为穿甲弹与复合装甲、装甲钢靶板相互作用和防护优化提供一定的参考。