基于改进能量熵的ESMD信号检测方法研究*
2019-11-13宿文才张树团贺英政
宿文才,张树团,贺英政
(海军航空大学, 山东烟台 264001)
0 引言
经验模态分解理论(EMD)由于其分解过程中包络线拟合偏差、端点拟合误差等原因导致分解结果存在严重的端点效应,并出现大量的虚假模态分量,导致EMD分解结果失真,从而严重影响其在工程领域中的应用,因此很多学者对EMD进行改进。Huang[1]等人提出了总体平均经验模态分解(EEMD),其在原始信号中加入大量的零均值白噪声来抑制端点效应和模态混叠问题,但并不能完全解决上述问题,并且重构误差较大[2]。Torres等人提出了互补集合经验模态分解(CEEMD),向信号中添加幅值相同、符号相反的高斯白噪声[3]。但多次添加随机噪声,计算量大,并且不可避免的存在噪声残留问题。
ESMD作为在EMD基础上改进的新方法,通过利用内部极点对称插值的方法来确定信号的包络线,能更好的降低由插值方式带来的拟合误差。其引入最佳自适应全局均线来优化剩余分量,残余量可以表征信号振动趋势,并由此确定最佳模态分解次数,以取得较好的分解效果[4]。目前,ESMD主要用于对海气通量[5]、声音特征提取[6]、故障诊断[7]、经济学分析[8]、混合储能配置[9]等领域的数据处理与分析。但ESMD在对故障信号分解时依然存在端点效应引起的模态失真以及模态混叠现象。
为解决上述问题,文中采用对称中点插值方法来替代ESMD内部极点对称插值,可有效缓解ESMD端点效应对分解模态内部的影响。针对ESMD分解存在的虚假IMF分量,提出基于改进能量熵对分解得到的模态分量进行虚假IMF识别,降低重构误差。经仿真分析,验证了提出的方法在信号检测的可行性和有效性。
1 改进极点对称模态分解方法
1.1 ESMD基本原理
ESMD算法具体分解流程如下[4]:
1)假设原信号为Y,依次连接相邻极值点,并将线段中点标记为Fj(j=1, 2,…,n-1) 。
2)通过线性插值的方式补充原始信号首尾边界中点F0与Fn,利用这(n+1)个中点构造p条插值曲线L1,L2,…,Lp(p≥1),取均值得到均值曲线L*。
3)对Y-L*重复上述1) ~2)步骤直到筛选次数达到最大值K或|L*|≤ε(ε为设定的容许误差),从而分解得到第一个模态分量M1。
4)将信号Y-M1重复步骤1) ~ 3) ,得到模态分量M1,M2,…,Mi和余量R。
5)设置K的变化区间[Kmin,Kmax],重复1) ~4)步骤,获取方差比率σ/σ0与K的变化关系。
6)取方差比率σ/σ0最小值时对应的刷选次数为K0,设置为最大筛选次数,重复1)~4)步骤,输出分解结果。
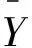
1.2 改进的ESMD
文献[6]提出的对称中点插值法可有效降低端点效应,其思想是根据ESMD极点中点插值(内包络)相对于极点插值(外包络)可减小端点对分解模态的影响,可在极点中点插值基础上再取一层内包络,进一步减小端点影响。具体步骤为:
1)标记并连接信号所有相邻极值点。
2)找出相邻极值中点,然后找出相邻极值中点的中点,用三次样条插值得到最终插值曲线。
假设原始信号为:
x(t)=cos(100πt)+4cos(256πt+π/3)
(1)
由图1可以看出:传统ESMD的IMF2分量曲线首尾“翘起”,端点效应程度较大。改进ESMD的IMF2分量曲线幅值整体都比较平稳,端点效应程度较小。由此可以验证改进ESMD方法抑制端点效应取得较为理想的效果。

图1 ESMD改进前后的分解结果
2 改进能量熵
2.1 传统能量熵
ESMD分解的各模态分量并不能严格按照频率依次分布,分解过程中还可能过分解导致大量低频IMF分量出现,造成模态混叠问题。因此,识别虚假IMF分量可有效改善ESMD分解中存在的模态混叠现象。
能量谱可表示各个状态变量在整个系统所占能量的比重。与原始信号相关性高的IMF占据主要能量,虚假IMF所占比例较小。通过构建能量熵函数表示各IMF所占的比例关系来区分虚假IMF分量。
能量熵识别虚假IMF分量的步骤如下[10]:
1)将原始故障信号用ESMD分解为N个IMF和一个残量R。
2)计算各IMF分量所占据的能量
(2)
式中,ci表示第i个IMF分量。
3)进行归一化处理
(3)
4)计算能量熵增量
Δqi=-p(i)log2(p(i))
(4)
能量熵增量较大的IMF可作为IMF有效分量,能量熵增量较小的IMF为虚假IMF分量。
2.2 改进能量熵
由能量熵识别虚假IMF分量的原理可知,能量熵在处理有效IMF能量与虚假IMF能量差别比较大时,识别效果较好,但是若原始信号含有弱信号成分,即有效IMF幅值较小,其能量熵必然较小,故能量熵不能将其余虚假IMF有效区分。由此,文中提出一种改进能量熵的方法来识别原始信号中的有效弱信号。
改进能量熵识别虚假IMF分量的步骤如下:
1)按照上述求取能量熵步骤求取各IMF分量所占据的能量E(ci)和能量熵增值Δqi。
2)求取最大能量值
计算IMF所有极大值点幅值的均值a和所有极小值点幅值均值b,IMF在时间t内的采样点为N,则最大能量熵为:
Emax(i)=N·(a2+b2)/2
(5)
3)标准化处理
(6)
4)计算IMF模态能量相对值
(7)
根据本征模态函数的定义,设定IMF分量应为标准模态函数。这里取标准模态函数为正弦函数,根据上述3)~4)步骤,求取一个周期内正弦函数最大能量熵的标准化处理结果为0.5,即PE=0.5。PE表示IMF能量与其匹配模态函数能量的相对值。
5)综合考虑能量熵增量和模态能量相对值
K=Δqi·P相对(i)
(8)
K为能量熵增量与IMF模态能量相对值的乘积,表示综合这两个指标的判断值,可以更有效的甄别虚假IMF分量。
3 仿真分析与应用
3.1 仿真信号分析
为验证文中所用方法的有效性,采用工频信号进行仿真验证,采样频率为12.8 kHz,采样时长为0.2 s。
(9)
式中:x1(t)为正常50 Hz工频信号;x2(t)为140 Hz信号;x3(t)为9倍工频的低幅高频谐波信号。
将该信号进行ESMD分解,结果如图2所示。改进ESMD将原始信号模态分解为5个IMF分量,通过各IMF分量首尾端点可以看出波动幅度平稳,端点漂移程度较小。
由图3可以看出:能量熵增量识别得到的主分量是IMF2和IMF3,模态能量相对值识别得到的主分量是IMF1~IMF3,而实际仿真信号有三个主要谐波成分,IMF1所对应的谐波信号x3(t)由于幅值较小,造成能量熵增量较小,但模态能量相对值高,从而识别存在误差。通过K值可识别出原信号的主分量为IMF1~IMF3,能量熵增量反映的是IMF能量在总能量的比重,而模态能量相对值反映的是IMF分量能量与匹配模态函数能量的相对值,将二者结合进行识别虚假IMF成分相比单独的能量熵增量识别度更高。
模态能量相对值只是表示IMF能量与其匹配模态函数能量的相对值,对于异常弱信号,其模态能量相对值可能较大,能量熵增量特别小,但对于工程应用无意义,因此识别虚假IMF分量需要结合实际情况,综合考虑能量熵增量和模态能量相对值。

图2 仿真信号改进ESMD模态分解图

图3 仿真信号IMF分量三种分析指标
3.2 实验仿真验证
为验证所提出方法的准确性,将该方法应用于采用MATLAB/Simulink搭建三相桥式整流电路。该整流电路的主要参数如下:三相交流电压源为100 V/50 Hz的交流电,串联相位相同的10 V/640 Hz谐波电压源,负载为阻感性负载,电阻为1Ω,电感为0.02 H,采样频率为100 kHz, 以整流后的电流为原始信号,仿真时间为0.5 s,取0.2~0.5 s的数据经改进ESMD分解后的结果如图4所示。
图4 整流信号改进ESMD分解结果
由图4可以看出:整流信号经改进ESMD分解后得到7个IMF分量和1个余量R,各IMF分量端点效应并不明显。
计算IMF的三种分析指标,结果由图5所示。能量熵增量识别的主分量是IMF1、IMF2、IMF3和IMF7。模态能量相对值识别的主分量是IMF1~IMF6。K值识别的主分量是IMF1~IMF3。因此能量熵增量和模态能量相对值都有识别误差,需要结合二者优势对IMF识别。

图5 整流信号IMF分量三种分析指标
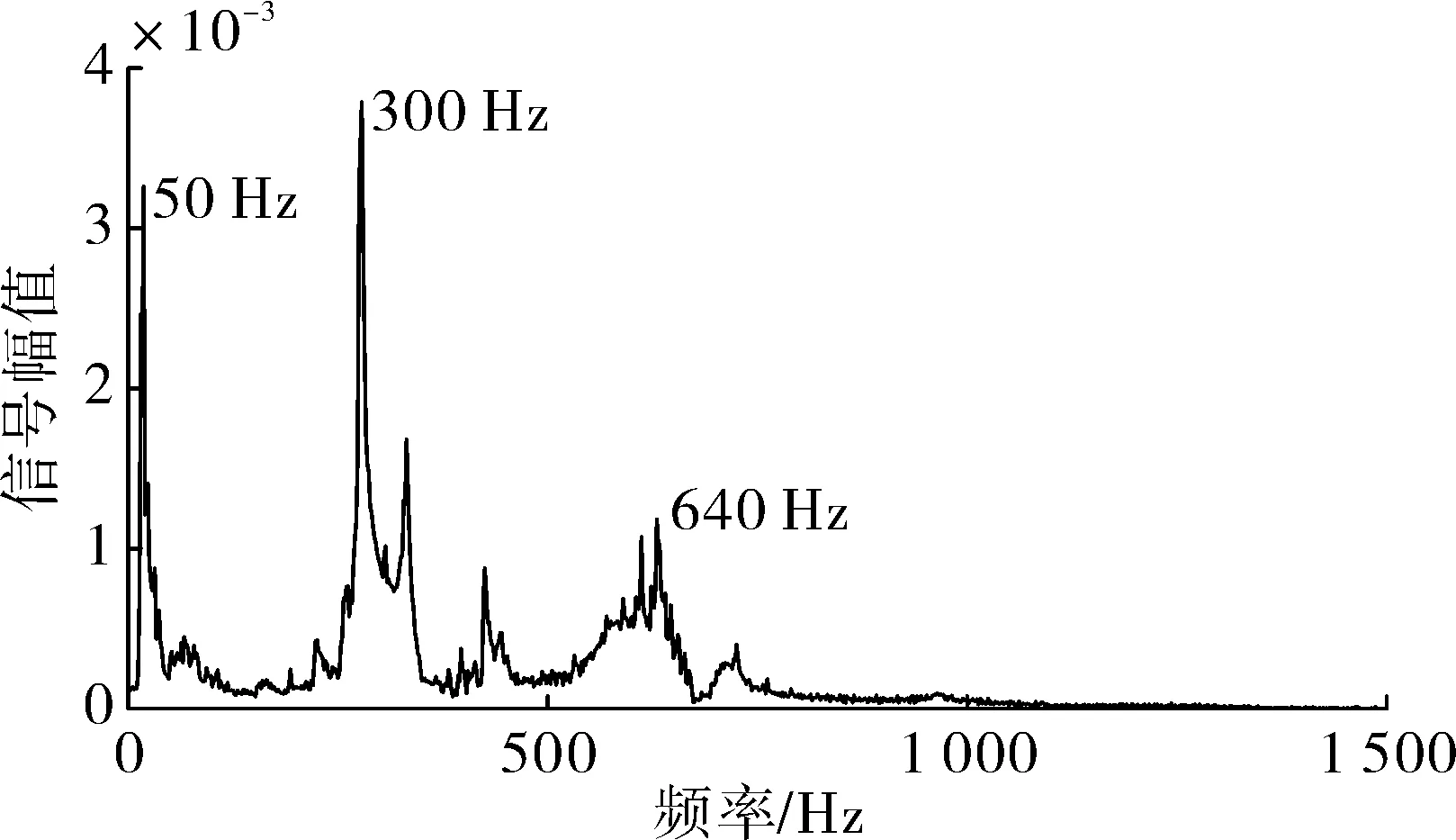
图6 整流信号边际谱
由图6可以看出:整流信号边际谱主要由3个信号组成,分别为工频50 Hz,6倍频300 Hz和谐波信号640 Hz。ESMD分解IMF的前提是该信号有多于5个极值点,工频50 Hz信号由于采样时间较短,极值点不超过5个,因此被分解在余量R中。6倍频300 Hz分量是50 Hz主电压源经整流后得到的。谐波信号640 Hz由于频率相对较高,相当于载波,经整流电路信号频率不变。
4 结论
文中针对ESMD处理故障信号存在端点效应和虚假IMF分量的问题,提出了一种基于改进能量熵增量的ESMD信号处理方法。该方法采用对称中点插值法抑制端点漂移,同时提出了一种改进能量熵增量的方法,将能量熵增量和模态能量相对值优势互补,有利于识别原信号中有效IMF分量。通过理论分析和仿真验证均表明该方法简洁易懂,识别度高,适用性强,能够较好地应用于故障信号检测。
