多线性约束结合自适应单脉冲测角方法

郑巧珍, 郭晓双, 邹小东, 王 鹏

(上海无线电设备研究所,上海201109)

0 引言

现代的相控阵雷达系统中,单脉冲测角技术可以对空域白噪声(各通道的噪声不相关且功率相等,即空域协方差阵为单位阵)背景下的单目标角度进行有效估计。然而,在高频雷达系统中,外界干扰和噪声(如宇宙噪声或杂波)占优,此时外界噪声为色噪声。在这种情况下,采用常规的固定参数和结构的信号接收系统来处理进入系统的外界干扰和噪声时,会带来较为严重的信噪比(signal-to-noise ratio,SNR)下降问题,增大测角误差。针对这一问题,通常采用自适应信号处理技术如广义旁瓣相消(GSC)[1]、自适应数字波束形成(ADBF)[2]、自适应空时二维信号处理(STAP)等来抑制干扰[3],提高SNR;但利用自适应信号处理技术完成干扰抑制的同时,带来了自适应和差方向图主波束畸变的问题,导致自适应单脉冲鉴角曲线出现畸变。

为了解决自适应单脉冲鉴角曲线畸变的问题,Nickel提出了自适应单脉冲特性的一阶Taylor展开表达式[4],该方法能够精确估计出和波束中心附近目标的角度,但对于主瓣内明显偏离波束中心的目标测角精度不高;Paine提出基于最小均方误差的目标方向搜索方法[5],以自适应地确定最优差波束权值,然而,该方法为得到校正的鉴角曲线需要很高的运算代价;Fante提出了一种三点线性约束的自适应处理方法[6],该方法能保证零点及3 dB波束宽度点的测角误差与真实值一致,属于方向图保形技术的自适应单脉冲测角算法,该算法实现较为简单,并且具有较高的精确度,易于工程实现等优点,得到广泛研究和应用,但该方法只对三点做了约束,除该三点外,其余角度的测角误差没有得到改善。为了兼顾干扰抑制效果与单脉冲测角性能,并有效应用于工程实现,本文提出一种在色噪声加干扰背景下的三点约束与导数约束结合的自适应单脉冲测角方法,该方法在抑制干扰的同时,选取零点和3 dB波束宽度点对鉴角曲线进行点约束,并对零点进行导数约束,改善了自适应单脉冲鉴角曲线的畸变问题。

1 自适应单脉冲测角

在自适应阵列信号处理中,最小方差准则是常用的统计最优波束形成准则之一,在此准则下得到的最小方差无失真响应(MVDR)波束形成器已广泛应用于雷达领域,它的思想是在保证期望信号方向增益一定值的条件下,计算最优权矢量使阵列输出功率最小。本文所用线性约束最小方差(LCMV)波束形成器是MVDR波束形成器的直接推广,LCMV波束形成器的权矢量可表示为

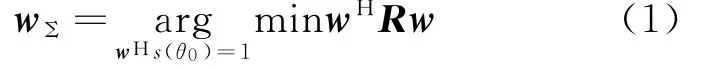
式中：θ0为期望信号方向(设-90°≤θ0≤90°),a(θ0)为θ0方向入射的阵列方向性矢量,其表达式为

用拉格朗日数乘子法求解式(1)得到LCMV权矢量：

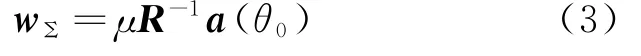
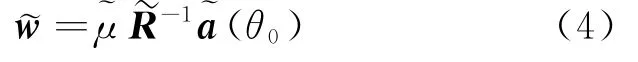
在一个窄带目标加K个干扰背景下,N元线阵接收信号为

式中：x为天线接收的信号;s,ji,n分别为目标、干扰和噪声。

理想情况下,无干扰,且噪声为白噪声,对应的理想单脉冲鉴角曲线为

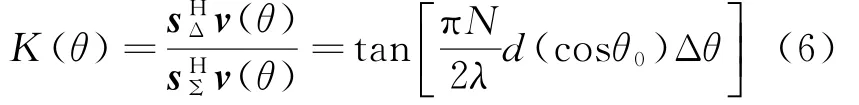
式中：sΣ,sΔ分别为阵列和、差波束导向矢量,θ0为主波束指向;Δθ为目标角度与主波束指向的差值,由式(6)可以得到Δθ的表达式为

色噪声及干扰背景下,信噪比下降、甚至目标为干扰所覆盖无法检测,采用自适应空域滤波可抑制干扰,提高信噪比,以此提高测角精度,满足最小方差准则的和、差波束自适应最优权矢量为

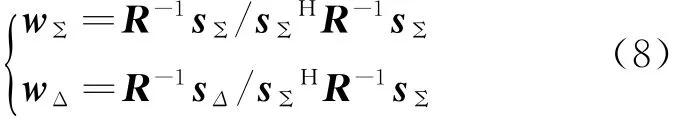
式中：R=E{x xH}为阵面接收信号协方差矩阵。由此可得自适应和差单脉冲测角的鉴角曲线为

虽然在色噪声及干扰背景下,自适应权矢量以最大限度抑制干扰和噪声,但较之理想鉴角曲线(式(6)),自适应单脉冲鉴角曲线(式(9))受到接收信号协方差矩阵R的影响,将产生畸变,即自适应单脉冲鉴角曲线不再具有理想线性特性,改善SNR下降带来的测角误差的同时,引入了新的角度估计误差。

2 多线性约束结合自适应单脉冲测角方法

本文采用对自适应单脉冲鉴角曲线进行线性约束的思想,以改善R带来的自适应单脉冲鉴角曲线畸变的问题。具体实现策略：对自适应单脉冲鉴角曲线进行点约束和导数约束,使其逼近理想鉴角曲线,保持自适应和波束不变,根据自适应和波束及约束条件,得到自适应差波束表达式。约束条件包括三个点约束(式(10)、式(11)、式(12))和一个导数约束(式(13)),其表达式分别为

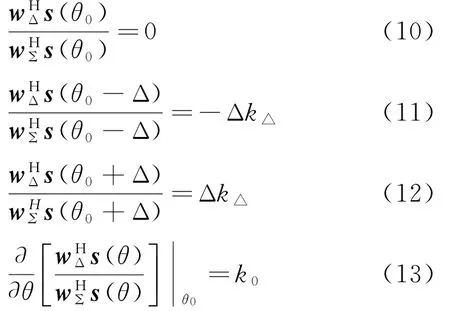
式中：θ0为主波束指向;s(θ)为入射角为θ的阵列方向性矢量;wΣ为自适应和波束加权矢量,其表示式如式(8)所示;Δ为3 dB波束宽度的一半;kΔ为理想鉴角曲线在(θ0±Δ)处的斜率;k0为理想鉴角曲线在θ0处的斜率。式(10)表示约束自适应单脉冲鉴角曲线,使其经过理想单脉冲鉴角曲线的零点;式(11)和式(12)表示约束自适应单脉冲鉴角曲线,使其经过理想单脉冲鉴角曲线的3 d B波束宽度的两端点;式(13)表示约束自适应单脉冲鉴角曲线,使其经过零点的斜率与理想鉴角曲线在该点处斜率一致。将式(10)～式(13)整理成线性约束的形式

式中：

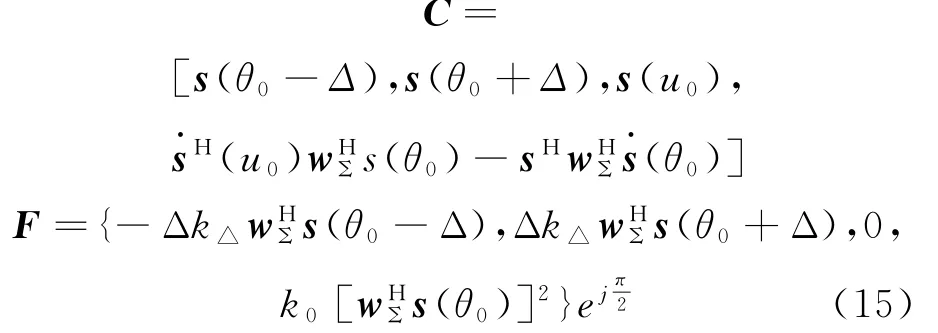
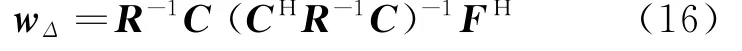
3 仿真结果

通过计算机仿真来分析本文多线性约束结合自适应单脉冲测角方法的性能。仿真参数设置如下：本文采用20个阵元的半波长均匀线阵进行简化仿真,目标位于1°,波束指向0°,阵元级信噪比为-20 dB;干扰位于-10°,干扰2位于20°,干噪比均为0 dB,3d B波束宽度为5°。仿真对比直接矩阵求逆算法(SMI),三点线性约束算法,以及本文算法的测角性能。

图1给出了3种自适应单脉冲算法的鉴角曲线对比图,如图所示,在没有加约束条件时,由于干扰协方差矩阵的影响,使得鉴角曲线偏离理想的鉴角曲线;加约束后的鉴角曲线和理想鉴角曲线吻合较好;在3 dB波束宽度内,较之三点线性约束算法,本文算法的鉴角曲线更接近理想值。

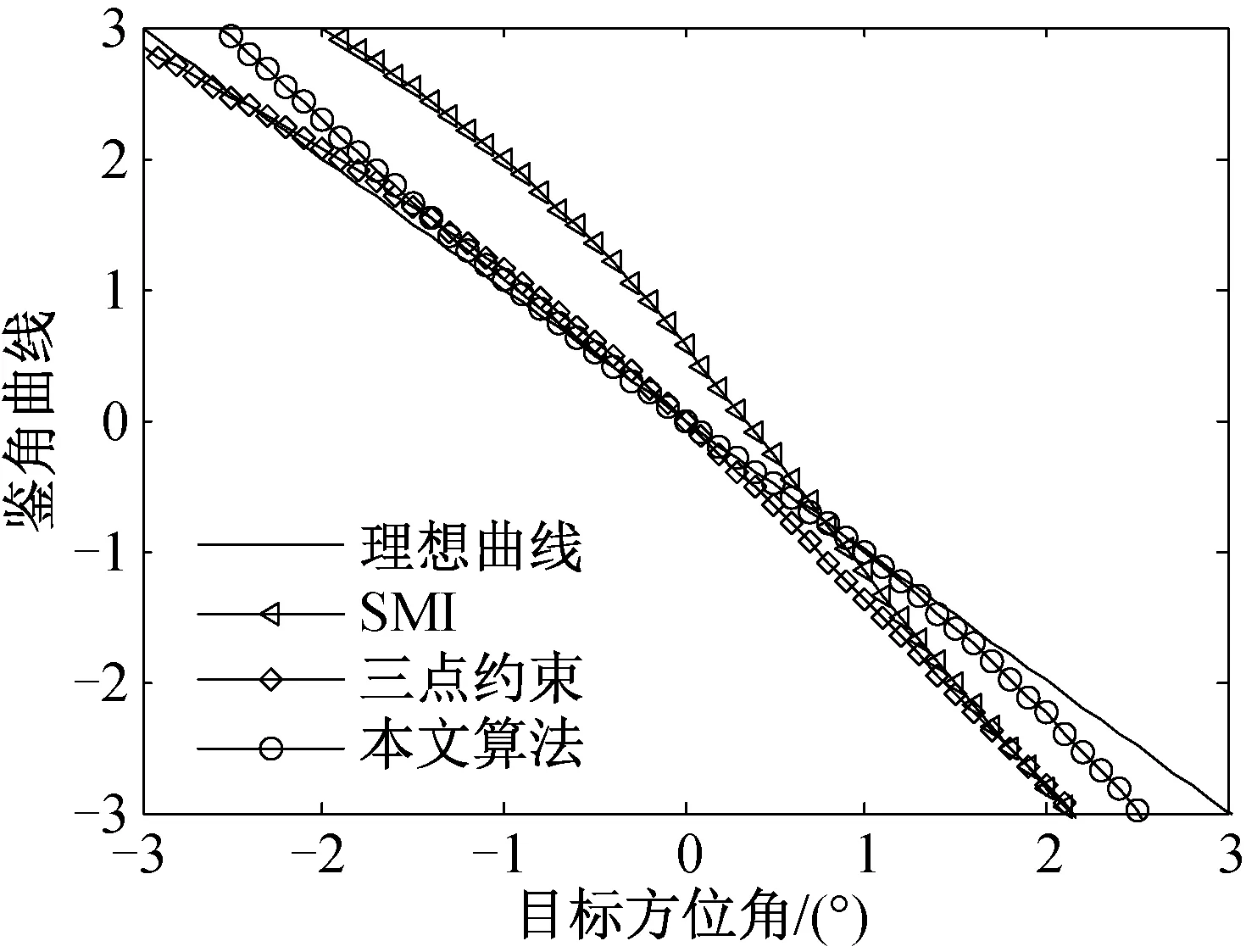
图1 鉴角曲线对比图

4 结束语

本文针对自适应单脉冲鉴角曲线畸变的问题,采用点约束与导数约束结合的方法,对自适应单脉冲鉴角曲线进行修正,完成干扰抑制的同时,使得修正后的自适应单脉冲鉴角曲线趋近于理想鉴角曲线,改善了自适应单脉冲鉴角曲线的畸变,通过仿真验证了本方法的有效性。该方法求解复杂度低,易于工程实现。