一种均匀共形天线阵列的测向方法

蒋 驰, 吴迎春, 陈 祎, 雷舒杰

(上海无线电设备研究所,上海201109)

0 引言

相对于主动探测系统,反辐射探测系统不需要发射电磁波,具有隐蔽性好、作用距离远、功耗小、抗电子干扰能力强等特点,是复杂电磁环境下,复合探测系统中不可或缺的组成部分。随着现代军事武器系统的高速发展,反辐射探测系统对天线构成体制的要求也是越来越高。反辐射天线体制主要包括旋转体制天线系统、共面天线体制以及共形天线体制。旋转天线通过时分复位技术进行测向,所需天线个数少,但实时性较低;共面天线与主动探测系统天线处于同一平面,占用了主动天线的空间,不适合系统小型化发展;共形天线位于系统的外围四周,所占空间小,且测向实时性高。因此,共形天线越来越多的使用受到了业界广泛的关注[1-3]。

受共形天线分布位置的限制,在角度较大时,电磁波的传播受天线罩以及系统结构的影响,会出现多路径、折射、绕射等电磁干扰现象,引起接收天线接收单元接收到的信号出现相位畸变,最终导致反辐射探测系统测向精度偏低、测角突跳等现象。同时,共形天线对入射电磁波的极化信息比较敏感,诸如多重信号分类(Multiple Signal Classification,MUSIC)等传统的测向算法在实际测向中会出现较大的误差,甚至失效。上述两大难题已经严重影响到了共形体制反辐射探测系统的精确制导[4-9]。

为了解决这一列问题,引入了相位匹配的思想,同时配合经典测向算法实现测向,具有计算量小、实时性高、抗干扰能力强以及空间分辨能力好等优点[10]。该方法预先输入一张全极化全空域的相位表,对共形天线所接收信号的相位进行匹配,确定目标的极化和初始角度位置,再利用相位表对该初始位置的相位进行相位补偿,将补偿后的相位作为输入,利用二维测向,最终确定目标的真实位置。

1 圆阵共形天线阵列

图1所示M个阵元均匀分布于半径为d的圆体周围。考虑到远场信号,信源足够远,则信号到达阵列各个天线时可认为是平行波。假设噪声与信号独立,且是加性独立同分布的高斯过程。

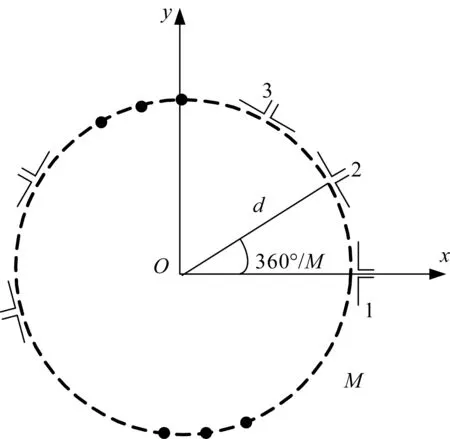
图1 均匀圆阵

如图2所示,空间有一远场辐射,对应的方位角和俯仰角分别表示为φ和θ,λ为信号波长,则可得到第m个阵元相对于阵元1的接收相位差φm。

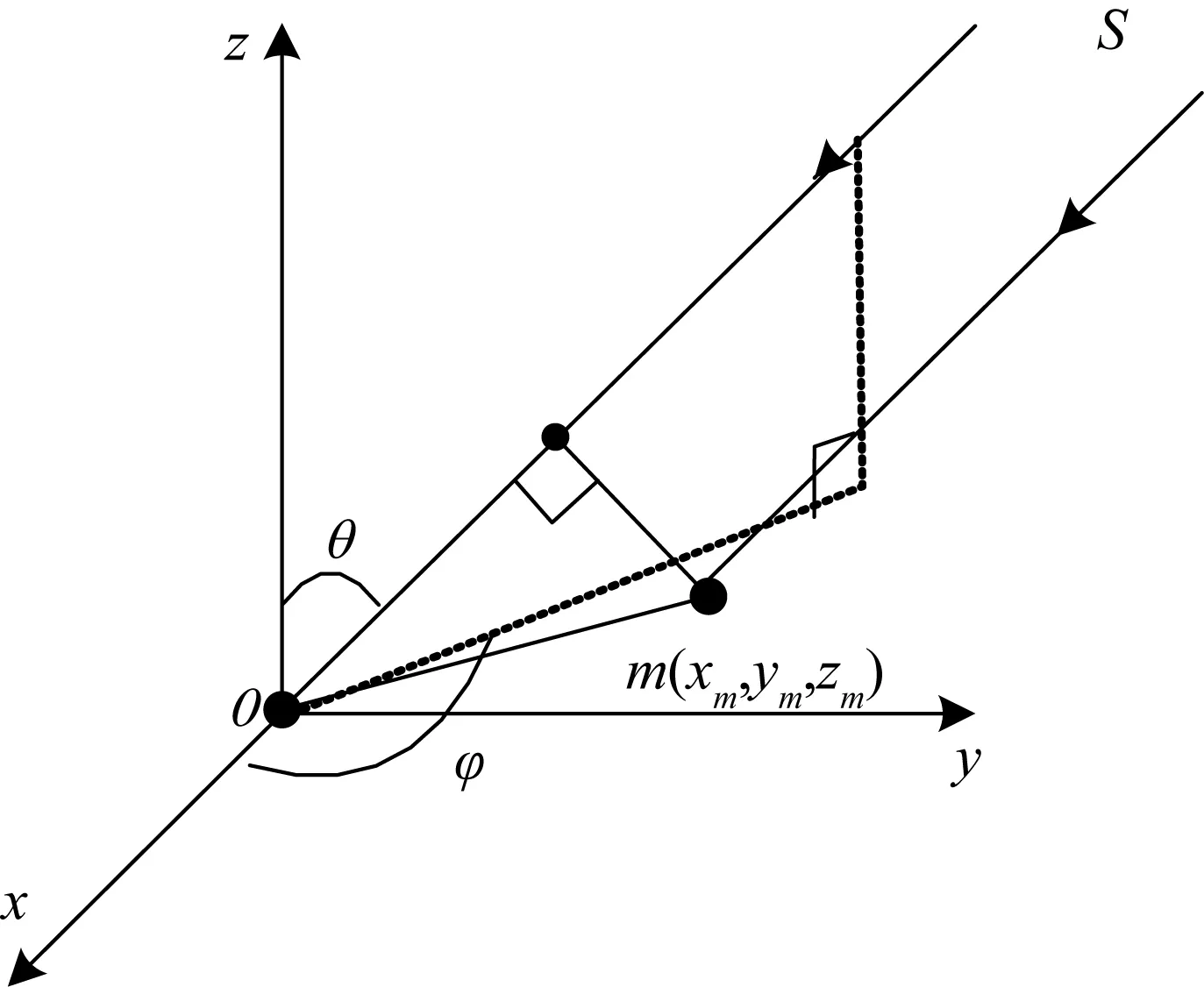
图2 测向空间直角坐标系

φm与阵元m相对阵元1的位置、系统结构影响、辐射源频率、极化以及角度相关,但在辐射源频率、极化和角度固定的情况下,各个阵元相对于阵元1的相位差是固定的。因此,可将极化域数字化为K等分,方位域数字化为P等分,俯仰域数字化为Q等分,从而建立起极化域、方位域、俯仰域三维表格,并在实验室暗室环境下测向。三维表格各点情况、各天线的相位差,表示为(k,p,q),其中k=1,2,…,K;p=1,2,…,P;q=1,2,…,Q;m=1,2,…,M,并作为校准数据存储。

2 传统MUSIC算法

如图1所示,以坐标系原点即圆阵的圆心为参考点,信号入射到阵列所在空间直角坐标系上的方 向 单 位 矢 量 为r=(sinθcosφ,sinθsinφ,cosθ),则信号入射到阵列的空域相移因子为

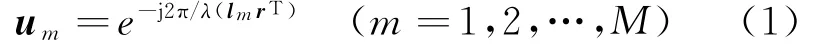
式中：[·]T表示转置;lm表示第m个阵元所在位置的坐标矢量,得到信号入射到阵列上时,第m个阵元相对于参考点的空域相移因子分别为gm。

定义极化域导向矢量为

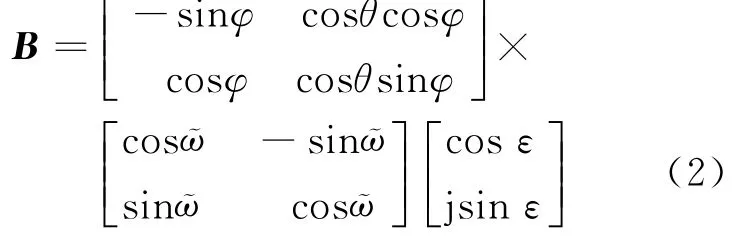
式中：ῶ和ε分别表示极化倾角和椭圆率角。则第m个阵元相对于参考点的输出增益为

从而得到阵列接收信号的导向矢量为

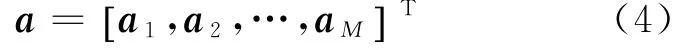
通过MUSIC算法构造的噪声子空间和阵列接收信号的导向矢量正交,设MUSIC算法构造的噪声子空间为UN,则有

式中：[·]H表示共轭转置。式(5)中的噪声子空间是通过对阵列接收数据的协方差矩阵R进行特征值分解得到的,而协方差矩阵R是根据有限次观测数据估计得到的,由于存在噪声的影响,实际测向中UN存在偏差,导致式(5)右边为非零向量。此时需要构造如下空间谱函数

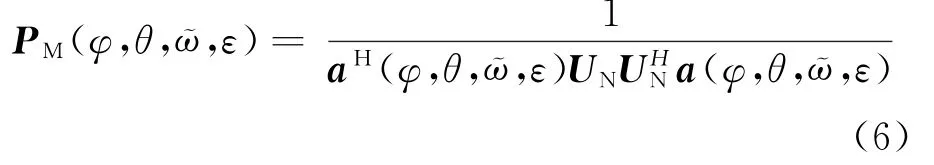
连续改变φ,θ,ῶ,ε的取值,构造式(6)对应的极化域、空间域谱并进行谱峰搜索,得到的极大值所对应的φ和θ就是目标信号的方位角和俯仰角。

3 相位匹配测向方法

不论是单脉冲干涉仪测向还是基于数据积的MUSIC算法测向,其测向前提为各个阵元接收的电磁波为平行波。由于系统环境的影响,辐射源发射的电磁波信号在天线阵元处并不能看做平行波,因此可以通过相位匹配的方法与测向算法相结合得到目标的精确角度。该测向方法主要分两步实现：首先,采用校准数据匹配得到目标初始位置,根据该位置的校准数据对相位差进行校准;其次,利用校准后的相位差数据作为测向输入,根据测向算法得到目标的精确角度。具体实现步骤如下。

3.1 相位匹配

现采用相位匹配的方法找到目标信号的初始位置。

定义相位几何距离

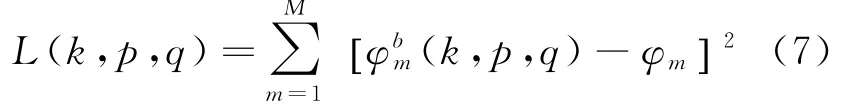
不失一般性,在实际计算相位几何距离时,采用T拍数据的相位数据作平滑处理后得到新的相位,表示为

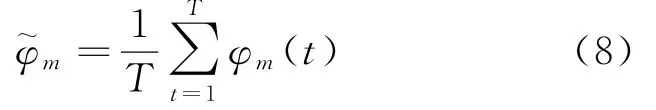
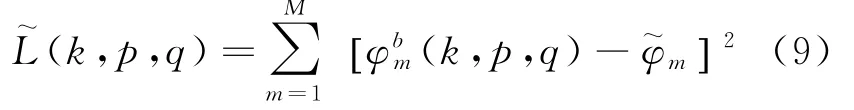
在k∈ [1,K]、p∈ [1,P]、q∈ [1,Q]的范围内遍历地比较全极化、全空域的相位表中的相位与接收信号相位几何距离。为提高相位匹配的效率,可将相位表按最大相位所接收的阵元进行如下分块

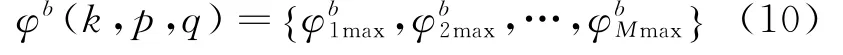
则平滑处理后的相位几何距离为

3.2 测向

由图1可得,在φ^m中选取阵元1～4所对应的相位,分别表示为γ1、γ2、γ3、γ4。

结合图2,阵元1和2的相位差为Δγ12=γ1-γ2,阵元3和4的相位差为Δγ34=γ3-γ4。则

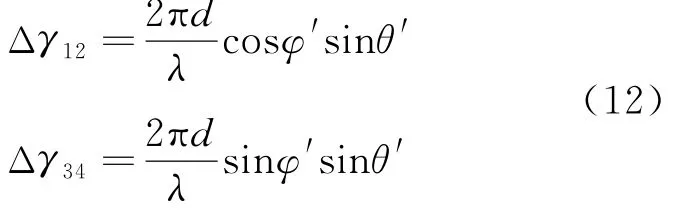
通过运算得出匹配校准后的方位角和俯仰角分别为

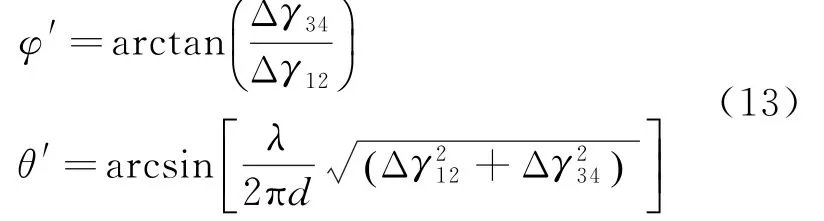
因此得实际接收的目标信号的真实方位角和俯仰角分别为

4 仿真对比

4.1 传统MUSIC算法仿真

仿真条件：目标信号为单频脉冲信号,极化固定为水平极化。俯仰角度固定为4°。目标方位向从-30°到30°缓慢变化,利用实测数据仿真结果如图3所示。

如图3所示,传统MUSIC算法可以实现反辐射探测系统在-20°～+20°范围内的有效测向,在20°以上则出现大的偏差和跳变。这是由于大角度时入射信号被弹体、天线罩等遮蔽引起了相位畸变所导致。

4.2 相位匹配测向方法仿真

仿真条件：目标信号为单频脉冲信号,极化固定为水平极化。俯仰角度固定为4°。目标方位向从-30°到+30°缓慢变化,利用实测数据仿真结果如图4所示。

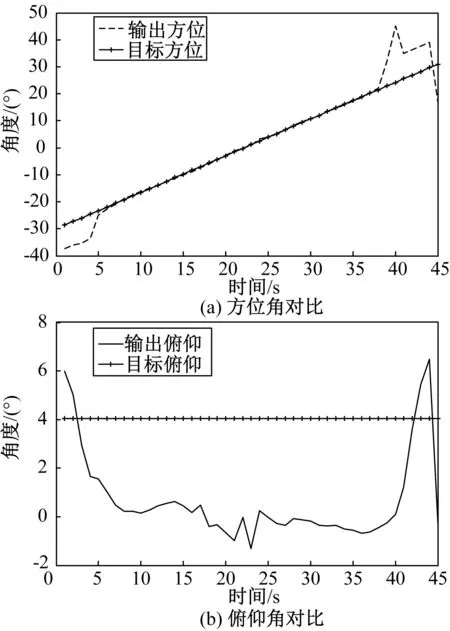
图3 传统MUSIC算法仿真结果

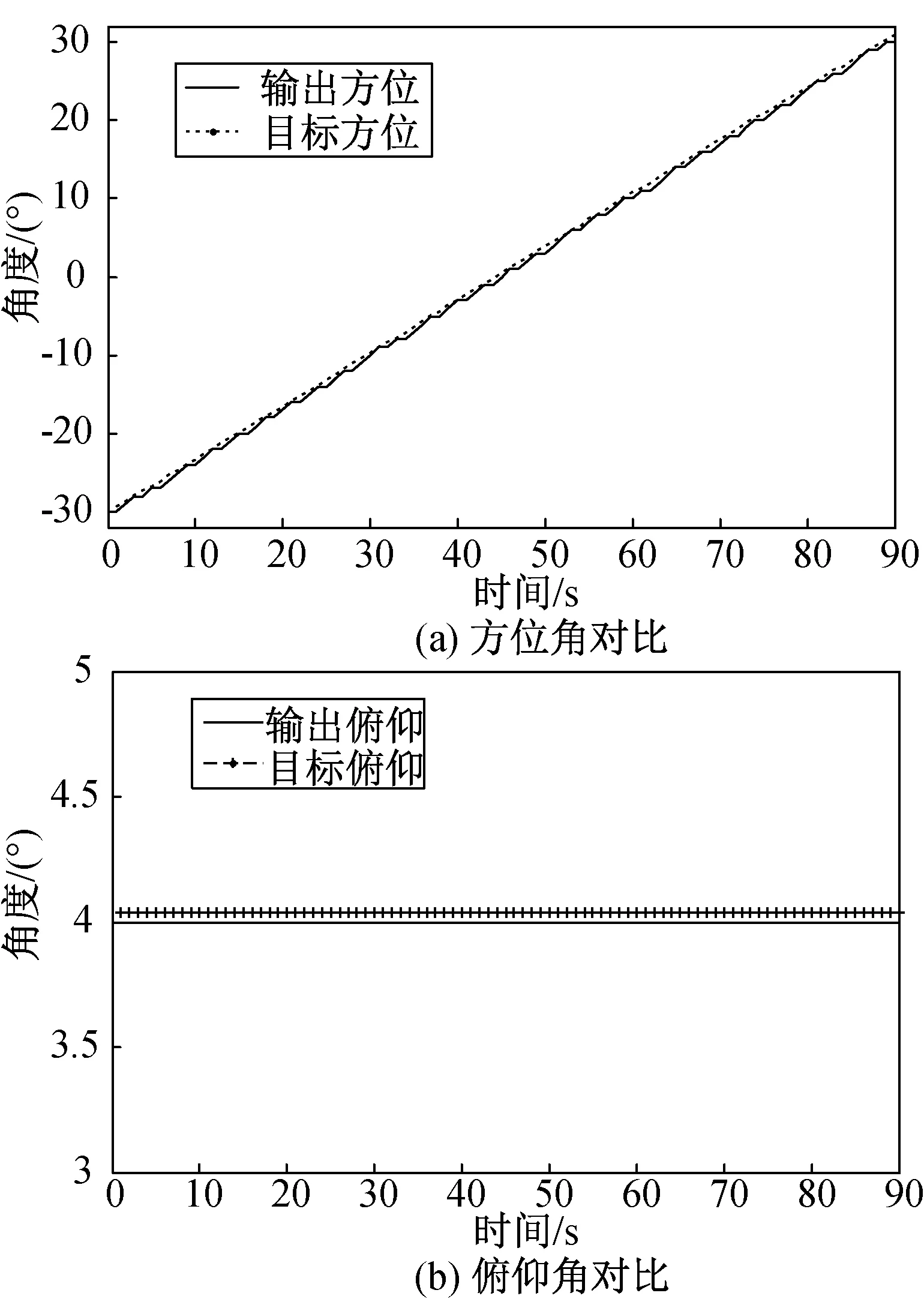
图4 相位匹配测向仿真结果

由图4可知,该方法可以实现反辐射探测系统在-30°～+30°范围内的有效测向。其中相位匹配得到的目标初始位置的角度和目标真实位置的角度有一定的偏差,而在此基础上经过测向后得到的角度基本与真实位置重合,误差非常小。

通过上述仿真对比,可以看出文中所提的测向方法具有较大的测向范围和较高的测向精度。

5 结论

基于共形天线排列的均匀圆阵模型提出了一种新的共形体制反辐射探测系统测向方法。利用相位匹配得到目标的初始位置,并利用该位置的相位校准数据进行相位校准,根据校准后的相位差计算得到目标的精确位置,可以实现目标信号的二维测向精确测向,同时可有效地识别信号的极化特征,并可以大概率地避免大角度测角时由于多路径、信号折射、绕射等情况下产生的噪声干扰,成功地对目标信号进行跟踪。