基于相变与真实气体模型的环形蒸汽引射器数值模拟研究
2019-11-12吴薇梵王占林孔凡超刘瑞敏张家仙
吴薇梵,王占林,孔凡超,刘瑞敏,张家仙
(1. 北京航天试验技术研究所,北京,100074;2. 北京市航天试验技术与装备工程技术研究中心,北京,100074)
0 引 言
研制上面级火箭发动机时,确定其高空特性是研制过程中的重要环节之一[1]。上面级火箭发动机工作时的环境压强低,需通过高空模拟试验建立相应高度下的低压真空环境才能真实获得其高空特性。因此,在高空模拟试验时,需对火箭发动机的真空舱进行抽吸,创造相应的真空环境。目前,采用的抽气装置有发动机-扩压器系统、发动机-扩压器-引射器(或机械真空泵)系统、低温泵-机械真空泵机组等[2]。目前应用较多的是发动机-扩压器-引射器系统。
国内外对高空模拟试验开展了大量的研究工作。随着计算机技术的快速发展,数值模拟手段被广泛应用于引射器流场的模拟和引射器参数的优化[3~7],部分结果得到了试验的充分验证[4~6]。刘盛田等[8]搭建了二维超-超引射器试验系统,获得了引射器混合室内流场纹影图;Stephens等[9]对二次喉道环形蒸汽引射器系统进行试验研究,确定了几何设计变量对系统启动和运行特性的影响。
随着行业的发展,在高空模拟试验中开始广泛使用蒸汽发生器,蒸汽不再是水蒸气,还含有酒精、CO2等多种组分。研究资料中大多采用理想气体的水蒸气进行数值模拟,缺乏对混合气体组分输运模型影响的研究,并且很少考虑水蒸气的凝结相变现象。虽然引射器研究成果很多,但环形引射器的研究资料相对较少,涉及组分输运及两相流动的理论分析和仿真更少。本文采用冻结流模型、组分输运模型、相变模型和真实气体模型,基于理论计算和数值模拟对环形引射器进行分析,并与试验结果进行对比。
1 计算模型
1.1 几何模型
图1为采用扩压器和蒸汽环形引射器方案的上面级发动机高空模拟试验系统。其中引射器长为10 900 mm,引射喷管喉部截面面积为38 111 mm2,混合室截面直径为 1104 mm,引射器出口截面直径为1561 mm。蒸汽由水/液氧/酒精蒸汽发生器提供。
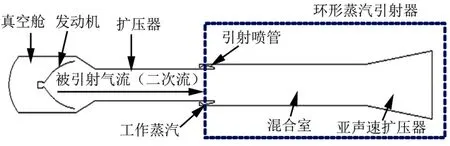
图1 高空模拟试验系统方案示意Fig.1 High Altitude Simulation Test System
1.2 网格无关性检验
本节用仿真软件Fluent进行流场计算,工作蒸汽采用纯水蒸气,理想气体。当残差曲线收敛,且引射器进出口流量及最大马赫数等几个重要参数曲线稳定不波动,可认为结果收敛,计算结束。网格无关性检验结果如表1所示。

表1 纯水蒸气仿真的网格无关性检验结果Tab.1 Result of Grid Independence Test for Simulation of Pure Water Vapor
由表1可知,几何模型的初始网格总数为2.5万个,采用结构化网格,壁面适度加密。网格划分方法不变,在初始网格的基础上增加不同倍数的网格数量(分别为2倍、4倍、6倍、8倍、12倍、16倍),然后监测表 1中的几个重要参数,通过对比这些参数的值来检验是否与网格无关。
通过表1中的数据可以看出,网格数量对仿真结果影响很大,当网格数低于15万个时,各监测参数值与高网格数的参数值存在较大差异;当网格数约大于20万个时,不同网格数下的参数变化和差异都很小,因此可以认为20万个的网格数可以达到网格无关性要求[10,11],计算区域网格划分如图2所示。

1.3 理论计算方法
引射器极限真空理论计算公式如下[2]:
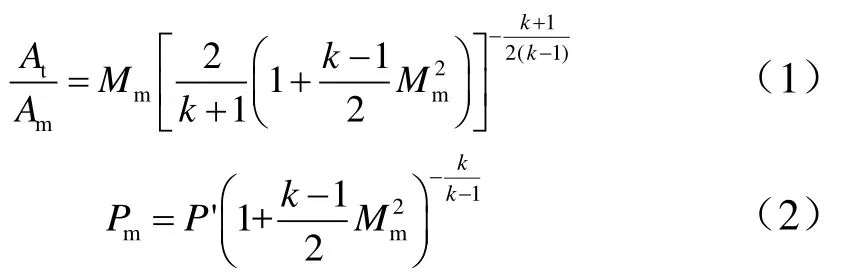
式中Am为混合室截面面积;At为喷管喉部截面面积;Mm为混合室马赫数;k为比热比;Pm为混合室静压;为混合室总压。
式(1)、式(2)中假设混合室静压为真空舱内压力,混合室总压为蒸汽入口压力。根据式(1)、式(2)即可求出真空舱压力。
1.4 仿真模型
1.4.1 控制方程
本文采用仿真软件Fluent对环形蒸汽引射器零二次流的流场进行模拟,控制方程为稳态二维轴对称雷诺平均Navier-Stokes方程,湍流模型选用Realizablek-ε模型[12]。采用二阶迎风格式对连续方程、动量方程和能量方程进行离散,采用 Coupled算法耦合求解。引射喷管入口边界条件采用压力入口,设定入口总温、总压和组分;引射器出口采用压力出口,给定出口。边界参数如表2所示,蒸汽化学成分如表3所示。

表2 环形引射器边界参数Tab.2 Boundary Parameters of Annular Ejector

表3 环形引射器工作蒸汽化学成分Tab.3 Chemical Composition of Working Steam of Annular Ejector
1.4.2 相变模型
图3为水的PT图。跨声速流动时,饱和水蒸气膨胀后温度压力降低,越过气液饱和线,部分蒸汽凝结;由于跨声速气流膨胀速率高,湿空气相变为非平衡凝结过程[13]。为简化研究,本文不考虑非平衡凝结过程中的液滴成核和生长等过程,假定为平衡凝结。

图3 水的PT图示意Fig.3 PT Diagram of Water
本文采用 Mixture相变模型和用户自定义函数(User-Defined Function,UDF)模拟相变过程。
水蒸气在气液饱和线上的压力温度计算方程为[14]
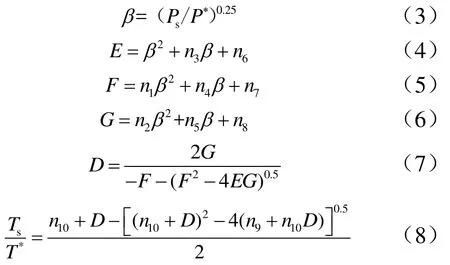
采用Lee模型模拟水蒸气和液相水之间的传质过程[15]:

若Tl>Ts(蒸发):
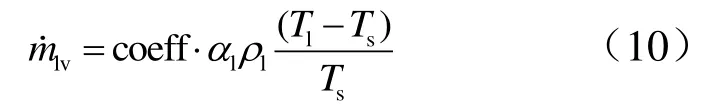
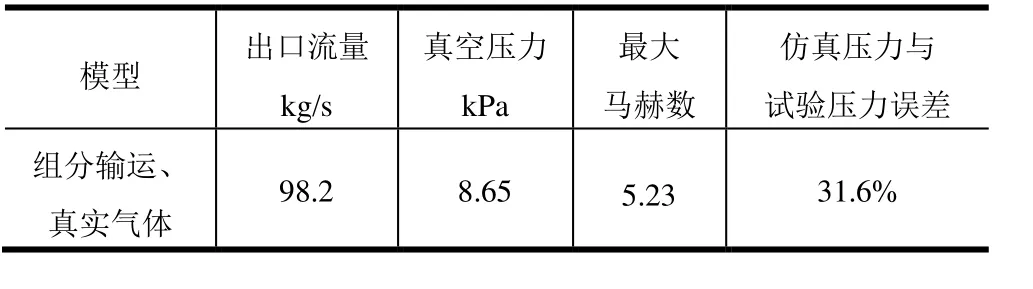
若Tv 式中 coeff为松弛系数。 1.4.3 真实气体模型 进入引射器的工作蒸汽温度和压力相对较高,采用理想气体有一定的偏差。为获得蒸汽引射时采用理想气体状态方程和真实气体状态的差异,提高真空压力预测精度,引入描述真实气体的 Redlich-Kwong状态方程进行比较分析[16]。修正后的通用形式为[17] 式中 P为绝对压力;Vm为比摩尔体积;T为温度;R为通用气体常数;b,c,δ,ε分别为临界温度、临界压力、偏心系数和临界比体积的函数;η为吸引系数,为温度的函数,通常写成η(T)。采用Soave-Redlich-Kwong三参数状态方程对式(12)进行修正[18],有: 式中 Tc为临界温度;Pc为临界压力;η0为临界温度、临界压力等参数的函数;ω为偏心系数;在Soave-Redlich-Kwong状态方程中:δ=b,c和 ε都为 0。 该环形蒸汽引射器典型试验结果及试验结果平均值如表4所示。 表4 环形蒸汽引射器典型试验结果Tab.4 Typical Test Results of Annular Steam Ejector 根据式(1),代入喷管喉部截面面积、混合室截面面积及工作蒸汽的比热比 1.305,计算出 Mm=4.446;再将混合室总压1.85 MPa代入式(2),求出真空舱压力4.80 kPa。与试验结果的平均值12.60 kPa相差较大。 分别采用冻结流模型和组分输运模型对蒸汽引射器进行对比分析。在冻结流模型中,将工作蒸汽假定成一种气体,其物性参数为:比热1806.255 J/(kg·K)、导热系数0.54925 W/(m·K)、粘度4.80039×10-5kg/(m·K)、摩尔质量19.615 kg/mol;在组分输运模型中,根据表3给定各气体组分,采用理想气体混合定律混合,不考虑相变。 计算过程均采用理想气体,马赫数分布如图4所示。 由图4可知,这两种模型中,引射器混合室内均存在斜激波和正激波:第1个斜激波最强,然后在中心轴上和它的对称激波相交,并反射向下游传播,斜激波沿下游方向逐渐减弱;正激波刚好出现在混合室与扩张段的交界面上。图4结果表明,两者区别不明显。表 5给出了两种计算模型下的主要参数。由表 5可知,除马赫数相差为3.7%以外,其余计算结果相差在1%以内。图5给出了冻结流模型和组分输运模型沿轴向坐标的压力和马赫数曲线,两种模型下的参数曲线基本重合。结果表明冻结流模型和组分输运模型计算结果接近,而与试验结果相比,两者与12.6 kPa均相差较大,误差超过30%。 表5 冻结流与组分输运计算结果Tab.5 Calculation Results of Frozen Flow and Component Transport 图5 冻结流和组分输运沿轴向坐标的参数曲线对比Fig. 5 Comparison of Parametric Curves of Frozen Flow and Component Transport Along Axial Coordinates 2.4.1 相变模型的影响 表6为在组分输运的基础上加入凝结相变模型的计算结果。图6为相变模型下的马赫数、液相水体积分数和温度的分布。对比图4b和图6a的马赫数云图可以看到,加入相变模型后,蒸汽凝结产生的水分会降低流动速率,导致马赫数减小,引射器引射能力降低,真空压力增加到11.32 kPa,与试验值相比误差为10.2%,精度大幅提升。且相变模型下斜激波的个数增多,正激波位置更接近出口。说明,在伴随有凝结相变现象发生的蒸汽流动中,应考虑凝结对流场造成的影响。 表6 相变模型计算结果Tab.6 Calculation Results of Phase Change Model 图6 基于组分输运和相变模型的云图Fig.6 Contours Based on Component Transport and Phase Change Model 2.4.2 真实气体模型的影响 表7为在组分输运的基础上加入真实气体模型的计算结果。相比表5中理想气体的计算结果,加入真实气体模型后,引射器出口流量和真空压力均增大,真空压力与试验结果的误差略有减小,但仍大于30%。对比相变模型,可以认为,真实气体模型对计算结果的影响不如相变模型的大。 表7 真实气体模型计算结果Tab.7 Calculation Results of Real Gas Model 2.4.3 相变模型加真实气体模型的影响 表8为相变模型加真实气体模型计算结果。由表8可知,引射器真空压力相比其它模型均增大,真空压力计算结果与试验结果更接近,误差缩小到 3.6%。图 7为在相变的基础上理想气体与真实气体沿轴向坐标的参数曲线对比。从图7a的对比曲线中可以看出,真实气体模型比理想气体模型产生了更多的液相水。结合图6和图7a可以看到,在激波前后,由于压强、温度变化梯度大,水蒸气发生凝结,液相水体积分数较大;从图7b中可以看出,两种模型的马赫数曲线基本重合。 图 7 理想气体相变与真实气体相变沿轴向坐标的参数曲线对比Fig.7 Comparison Results of Parametric Curves of Ideal Gas and Real Gas Based on Phase Change Model Along Axial Coordinates a)环形引射器真空压力的理论计算结果与实际试验结果差别较大,理论值4.80 kPa明显低于试验平均值12.60 kPa。 b)基于理想气体的冻结流模型与组分输运模型,二者仿真结果差别很小,各参数曲线基本重合,流场基本一致,可以认为在仿真时选用以上两个模型对结果的影响差别不大,误差均超过30%。 c)引入相变模型和真实气体模型对计算结果均有影响,相变模型的影响大于真实气体模型。引入相变模型后,马赫数减小,蒸汽流速减慢,真空压力升高,流场中斜激波个数增多,正激波更靠近出口,并且在激波面上有较多液相水析出。相比之下,真实气体模型的影响较小,但是比理想气体的计算结果更接近试验值。 d)基于组分输运加入相变模型和真实气体模型,随着模型越来越接近实际情况,真空压力越来越高,仿真结果更接近试验值,最终误差为3.6%。
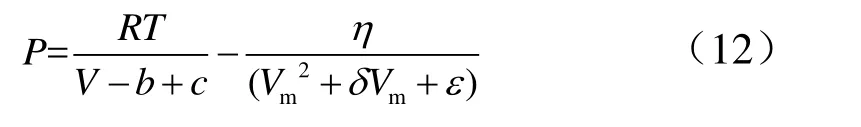

2 结果分析
2.1 试验结果
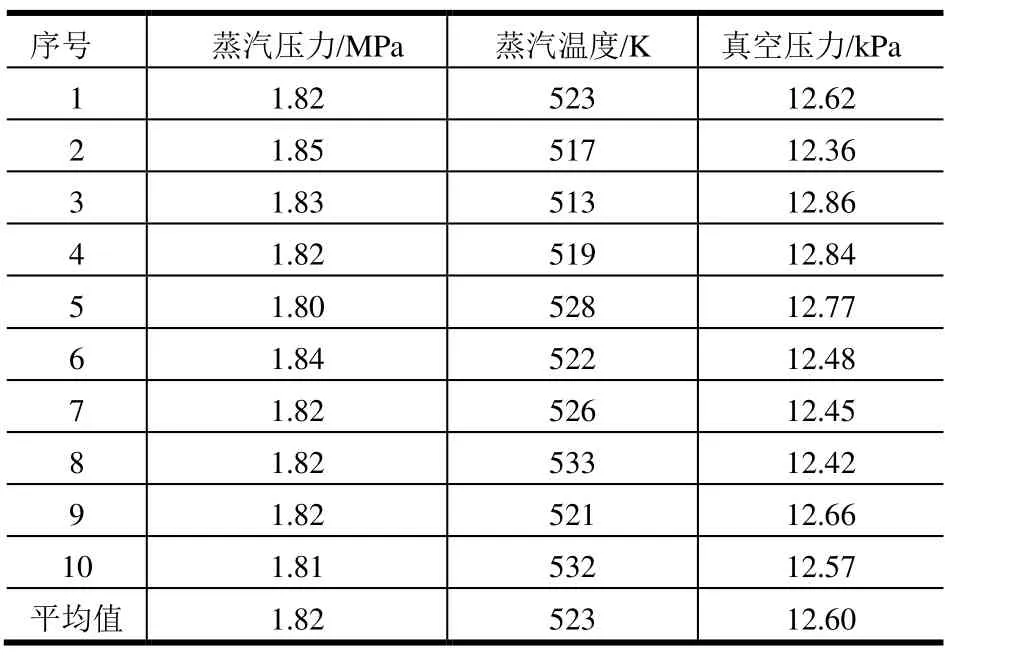
2.2 理论计算与试验结果
2.3 材料模型的影响分析



2.4 物理模型的影响分析



3 结 论
