多平面升力体外形设计与气动/隐身性能研究

薛 普，杨依峰，王锁柱，苏 伟，甄华萍

（北京航天长征飞行器研究所，北京，100076）

0 引 言

目前，高超声速技术研究是世界各国都在开展的研究热点。其中，德国宇航中心的高超声速再入飞行试验项目“锐边”（Sharp Edge Flight Experiment,SHEFEX）采用尖前缘多平面组成的新型飞行器结构进行防热材料和结构的测试，并利用飞行试验数据对数值模拟和地面测试结果进行验证[1]。

图1为SHEFEX系列发展路线图。其中，SHEFEX1飞行试验通过尖外形探索提升飞行器气动特性的途径；SHEFEX2飞行试验则用来验证气动力控制高超声速飞行技术。2005年和2012年，德国航空航天中心成功进行了 SHEFEX-I和 SHEFEX-II试验[2]。SHEFEX所采用的多平面布局飞行器既能实现气动力/热性能的提升，同时会引起雷达隐身性能的改变。美国的F117隐身战斗轰炸机就是采用多平面外形实现雷达隐身性能提升的典型实例。虽然综合作战性能的不足导致了F117的退役，但多平面布局在高超声速飞行器上仍具备一定的应用前景。因此，需针对多平面布局高超声速飞行器开展气动/隐身性能研究。

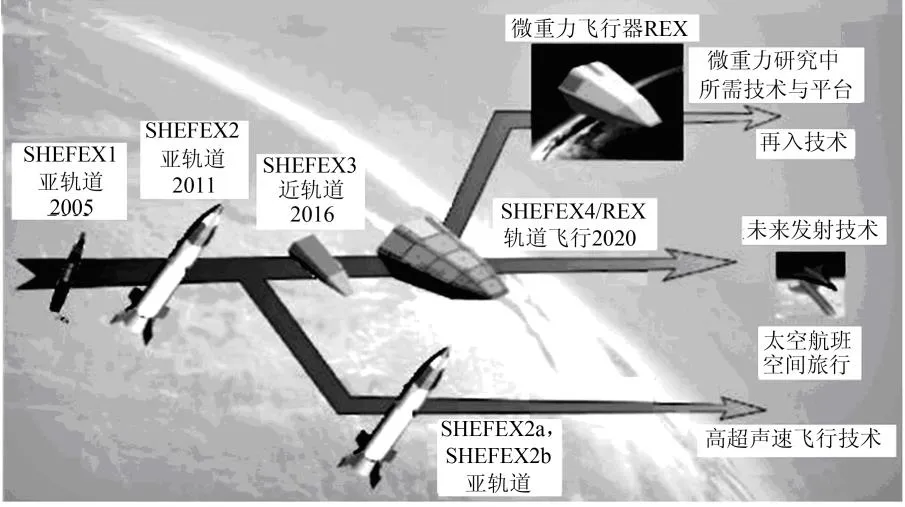
图1 德国SHEFEX系列发展路线图Fig.1 Roadmaps of SHEFEX

本文基于一种具有精确解析解的圆锥流场生成的乘波体（Waverider Vehicle，WRV）利用多平面设计方法生成一种多平面升力体（Multi-planar Lift-body Vehicle，MLV）。针对多平面升力体和乘波体开展气动/隐身性能对比分析，采用基于层流方程的数值计算方法开展基本气动特性的研究，采用基于物理光学法的雷达散射截面（Radar Cross Section，RCS）仿真开展雷达隐身特性的研究，研究结果表明多平面升力体同时具备较好的气动与隐身性能，可为高超声速飞行器气动外形设计提供一种可行方法。

1 多平面外形设计方法

乘波构型是可以突破升阻比屏障的高超声速飞行器[3]，通过具有精确解析解的流场（平面楔形流场、圆锥流场和“Λ”翼形流场等）设计获得。本文采用圆锥流场作为基准流场，利用 Taylor-Maccoll流动模型[4]求解生成一种锥导乘波体。以此乘波体为基础，将不同截面的形状调整为多边形，并利用多截面曲面将相邻截面进行拟合生成多平面升力体外形。多平面外形设计应当遵循以下原则：

a）相邻截面拟合形成的曲面应由多个平面相连形成，确保生成的外形为多平面外形；

b）不同平面交接处进行倒圆，以便降低RCS水平；

c）截面形状进行调整以防止下表面泄压严重；

d）不同截面进行形状调整时应确保装填空间不受影响；

e）锥段之间进行适当的锥角调整以保证较好的气动特性。

表1为基于上述原则设计的MLV与WRV的外形参数对比。

表1 MLV&WRV外形参数对比Tab.1 Configuration Comparison of MLV&WRV

图2为MLV与WRV底部截面形状对比。由表1和图2可知：MLV与WRV的长、宽、高、底部面积等主要参数保持一致，确保二者的装填空间不受影响；截面形状采用多边形+倒圆设计；下表面夹角变大，确保下表面有较高的压力。

图2 底部分截面形状对比Fig.2 Comparison of Bottom Shape

2 基本气动特性

基于层流方程对MLV与WRV的基本气动特性进行对比研究，从而得到MLV的升阻特性和静稳特性。利用有限体积法针对控制方程进行空间离散，离散格式采用Roe格式。计算状态选择典型高超声速飞行器飞行状态：高度H为60 km，马赫数Ma为6和8，计算攻角α为-2~10°，侧滑角β为0°、2°和5°。

2.1 升阻特性

图3~5分别为MLV与WRV无侧滑、马赫数为6和8时升力系数、阻力系数和升阻比随攻角变化曲线。

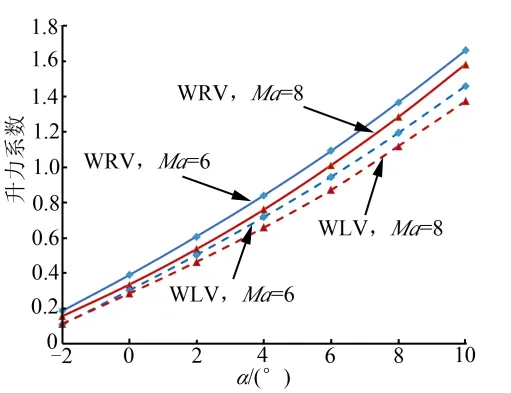
图3 MLV/WRV升力系数（β=0°）Fig.3 Lift Coefficeint of MLV/WRV（β=0°）

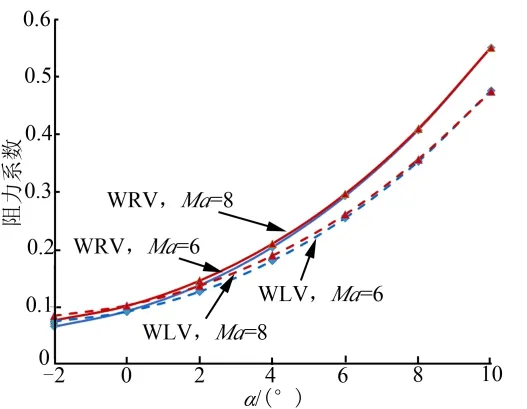
图4 MLV/WRV阻力系数（β=0°）Fig.4 Drag Coefficeint of MLV /WRV（β=0°）

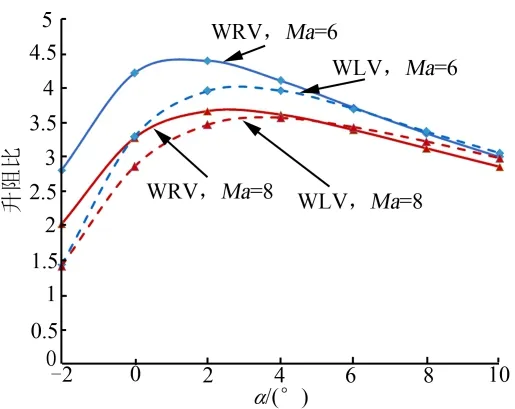
图5 MLV/WRV升阻比（β=0°）Fig.5 Lift-Drag Ratio of MLV/WRV（β=0°）

由图3~5可知，相比WRV，MLV的升力整体减小约 15%；阻力在攻角小于 2°时基本不变，攻角大于 2°时减小约 13%；升力减小、阻力先不变后减小的规律使升阻比在攻角小于4°时减小，攻角大于4°时变化不大；最大升阻比减小约 10%；最大升阻比对应攻角由1°增大至3°。

图6为MLV不同侧滑角时升阻比随攻角变化曲线。

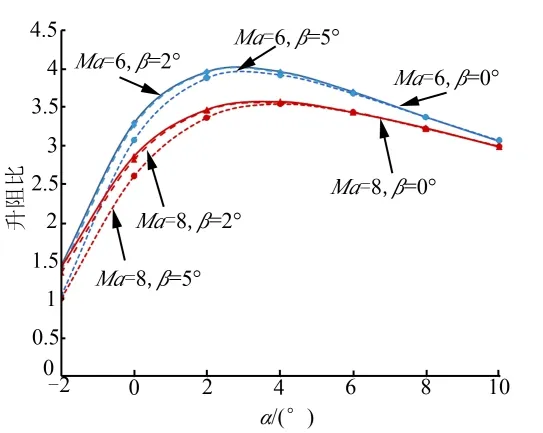
图6 MLV升阻比Fig.6 Lift-Drag Ratio of MLV

由图6可知，在计算状态高度H为60 km、马赫数Ma为6和8时，随着侧滑角的增大，小攻角时升阻比略有下降，大攻角时升阻比基本一致，最大升阻比的值略有降低；在计算状态下，最大升阻比变化范围为3.48~4。

相比WRV，在高度H为60 km、马赫数Ma为6和8时，多平面升力体最大升阻比减小约10%，最大升阻比的对应攻角增大；侧滑角引起多平面升力体的最大升阻比略微降低；在计算状态下，最大升阻比变化范围为3.48~4，具备较高的升阻比。

2.2 纵向焦心系数和航向压心系数

图7为MLV与WRV在马赫数Ma为6和8，侧滑角β为0°时的纵向焦心系数随攻角变化曲线。

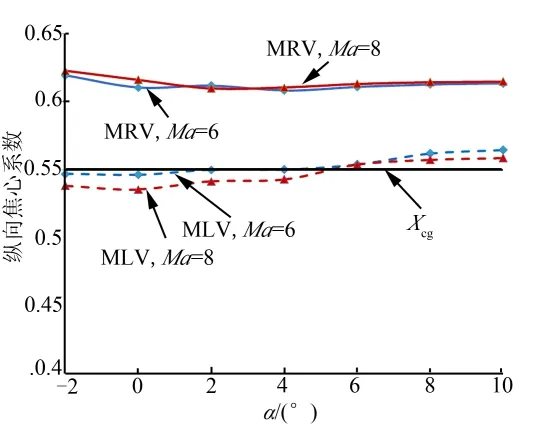
图7 MLV/WRV纵向焦心系数（β=0°）Fig.7 Longitudinal Pressure Center of MLV/WRV（β=0°）

由图 7可知，MLV的纵向焦心系数变化范围为0.536~0.565，WRV的纵向焦心系数变化范围为0.608~0.623，相比WRV，多平面升力体纵向焦心位置前移约6%，变化范围由1.5%增大至2.9%；质心系数取0.55时，纵向静稳定裕度变化范围为-1.4%~1.5%；小攻角时，多平面升力体处于静不稳定状态，控制系统设计考虑采用静不稳定控制。

图8为MLV不同侧滑角β为0°、2°和5°时纵向焦心随攻角变化曲线。由图8可知，相同马赫数不同侧滑角时，纵向焦心系数变化范围和变化趋势基本不变。

图8 MLV纵向焦心系数Fig.8 Longitudinal Pressure Center of MLV

图9 为MLV与WRV航向压心系数（侧滑角β为2°时）随攻角变化曲线。由图9可知，MLV航向压心系数变化范围为 0.595~0.630，WRV航向压心系数变化范围为0.630~0.656，MLV航向压心系数相对前移约3%；质心系数Xcg为0.55时，航向静稳定裕度变化范围为4.5%~8.0%。

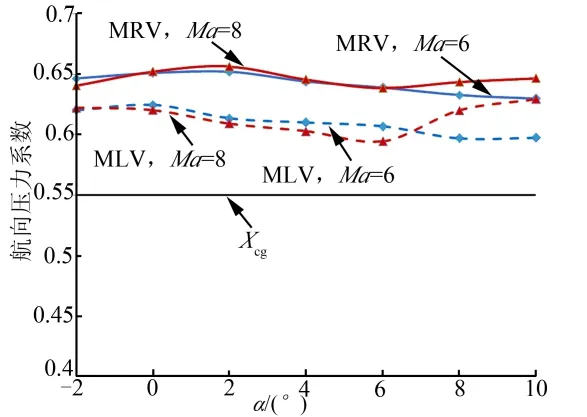
图9 MLV/WRV航向压心系数（β=2°）Fig.9 Lateral Pressure Center of MLV/WRV（β=2°）

图10 为MLV不同侧滑角（β为2°和5°时）情况下航向压心随攻角变化曲线。由图10可知，不同侧滑角时航向压心变化范围基本不变。

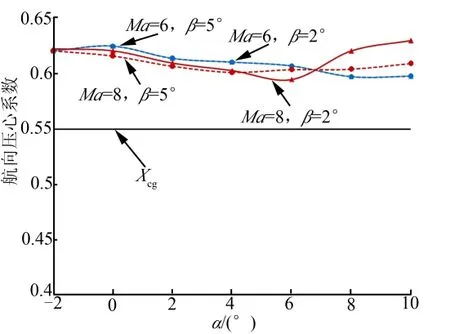
图10 MLV航向压心系数Fig.10 Lateral Pressure Center of MLV

结合图6、图8和图10发现：与0°侧滑相比， 2°和5°侧滑时升阻比略微减小，纵向焦心和航向压心处在相同变化范围；航向静稳定裕度较大，控制系统设计可以不考虑航向控制。

相比WRV，MLV纵向焦心相对前移约6%，航向压心相对前移3%；质心系数取0.55时，纵向静稳定裕度较小，变化范围为-1.4%~1.5%，小攻角时需进行静不稳定控制；航向静稳定裕度相对较大，变化范围为4.5%~8.0%，侧滑角未对升阻比、纵/航向静稳定裕度产生明显影响。

3 雷达隐身特性

RCS是衡量飞行器雷达隐身特性的重要参数，用于表征目标对雷达照射电磁波的散射能力[5]。对多平面升力体，前下方角域范围（俯仰角θ为60~120°，偏航角φ为-45~45°）是雷达波照射最重要的威胁方向[6]；多平面升力体飞行距离远，照射雷达通常为作用距离远的高频雷达，故选用高频算法作为雷达隐身特性评估方法。

物理光学法（Physical Optics，PO）是一种对目标表面电磁感应场进行近似并求解 Stratton-Chu积分方程实现散射场计算的高频算法[7]。PO的计算速度快，对电大尺寸的电磁散射问题求解有较大的优越性。矩量法（Method of Moments，MOM）是一种将连续方程离散化为代数方程组的方法，对于求解微分方程和积分方程均适用。MOM有很高的计算精度，是被公认电磁问题数值计算方法中最精确的算法，得到的电磁问题解常被当作精确值，以衡量其他算法的精确度；但MOM计算量、计算时间及耗费的内存较大。本文利用NASA标模对两种算法的适用性进行对比分析。

3.1 标模RCS计算

NASA标模Ogive是用于测试RCS计算结果的常用标模。Ogive半张角为22.62°，半长12.7 cm，最大半径2.54 cm。

Ogive模型的剖面轮廓曲线由以下表达式确定：

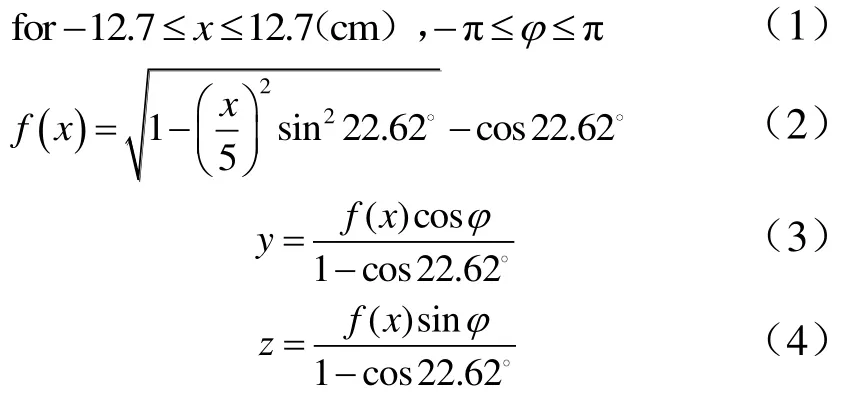
根据上述剖面建立的Ogive计算模型如图11所示。

图11 Ogive模型示意Fig.11 Ogive Model

分别利用PO和MOM对Ogive进行RCS计算。入射波为平面波，单站入射，入射波极化方式为水平极化，俯仰角θ为-90~90°，入射频率为9 GHz，表面材料选用金属良导体，标模计算结果如图12所示。

图12 Ogive单站RCS（f=9GHz）Fig.12 RCS of Ogive（f=9GHz）

由图12可知，基于PO的RCS计算结果与文献中基于PO的RCS计算结果的量值与变化规律均保持一致；采用PO和MOM的RCS计算结果在俯仰角θ为-30~30°时数值和变化趋势均保持一致；在θ为-90~30°和θ为30~90°时，采用PO计算得到的RCS明显偏小。原因在于采用PO进行RCS计算时，能够较好地计算出反射波，没有考虑尖端散射和边缘绕射的影响。多平面升力体和乘波体分别采用平面和大曲率曲面，影响RCS结果的主要因素是反射波。因此，本文采用PO计算多平面升力体和乘波体的RCS。

3.2 RCS计算

由于前下方角域范围是雷达波照射最重要的威胁方向，因此利用PO针对多平面升力体和乘波体在俯仰角θ为60~120°，偏航角φ为-45~45°范围内的RCS进行计算。入射波为平面波，单站入射，极化方式为水平极化，入射频率6 GHz，表面材料为金属良导体。多平面升力体RCS计算结果如图13所示。由图13可知，多平面升力体在俯仰角θ为60~120°，偏航角φ为-10~10°范围内出现峰值区域，而其他角域范围内 RCS均大幅减小。根据计算结果，RCS峰值为-12.26 dB，出现在（θ=117°，φ=±3°）处；RCS 平均值为-31.49 dB·m2。

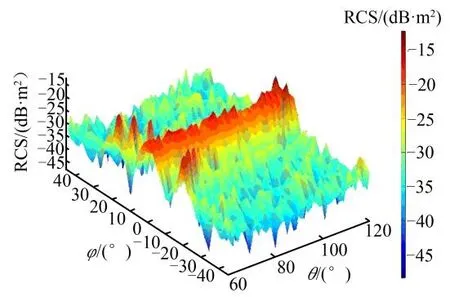
图13 MLV单站RCS云图（f=6GHz）Fig.13 RCS Nephogram of MLV

乘波体RCS计算结果如图14所示。

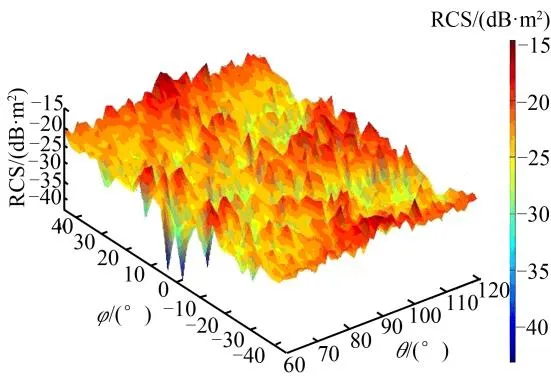
图14 WRV单站RCS云图（f=6GHz）Fig.14 RCS Nephogram of WRV（f=6GHz）

由图14可知，在俯仰角θ为100~120°，偏航角φ为-10~10°和俯仰角θ为 90~100°，偏航角φ为±20~±40°范围内，乘波体 RCS相对较大。根据计算结果，RCS峰值为-14.67 dB·m2，出现在（θ=90°，φ=±45°）处；RCS 平均值为-23.63 dB·m2。

对比图13与图14可知，乘波体的RCS分布更加平均，而多平面升力体RCS较高的部分主要集中在正前方角域俯仰角θ为60~120°、偏航角φ为-10~10°范围内。

表2为多平面升力体与乘波体的RCS计算结果对比。由表2可知，多平面升力体相比乘波体平均RCS减小 8 dB·m2，最大 RCS相近，而最小 RCS则减小5 dB·m2。

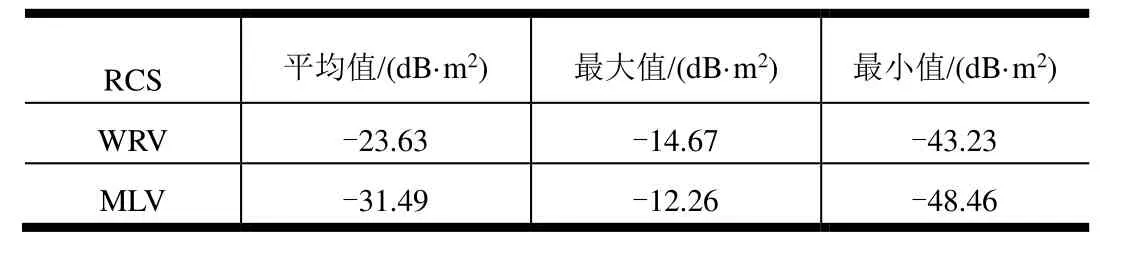
表2 RCS计算结果对比Tab.2 Comparison of RCS Results

依据雷达散射理论[8]进行分析可知，正对散射面方向上的雷达散射幅度较强，气动布局的多平面化使较强的雷达散射幅度集中在某些区域上，降低了其他区域的雷达散射强度，从而降低了整体RCS水平。

综上：相比乘波体，多平面升力体可以实现RCS的整体减缩，在特定角域俯仰角θ为60~120°、偏航角φ为-10~10°范围内RCS较大，飞行过程中可通过姿态控制避开此角域，进一步降低多平面升力体被高频雷达探测到的可能。

4 结 论

本文基于一种乘波体外形利用多平面方法生成一种多平面升力体，并对二者开展气动/隐身性能对比研究。基于层流方程完成了基本气动特性的数值计算，基于PO完成了RCS的仿真计算，结果表明采用本文的多平面设计方法生成的多平面升力体具备较好的气动和隐身性能，研究结果如下：

a）飞行高度为60 km、飞行马赫数为6和8时，相比乘波体，多平面升力体最大升阻比减小约 10%，最大升阻比对应攻角增大，侧滑角引起多平面升力体的最大升阻比略微降低；在计算状态下，最大升阻比变化范围为 3.48~4.0，具备较高的升阻比；纵向焦心相对前移约6%，航向压心相对前移3%；质心系数取0.55时，纵向静稳定裕度较小，变化范围为-1.4%~1.5%，小攻角时需进行静不稳定控制；航向静稳定裕度相对较大，变化范围为 4.5%~8.0%，侧滑角未对升阻比、纵/航向静稳定裕度产生明显影响。

b）相比乘波体，多平面升力体可以实现 RCS的整体减缩，在特定角域范围俯仰角θ为60~120°、偏航角φ为-10~10°内RCS较大，飞行过程中可通过姿态控制避开此角域，进一步降低多平面升力体被高频雷达探测到的可能性。