基于轨迹优化的返回式滑翔飞行器最小航程影响因素分析

许泽宇，王洪波，康永来，李建府，李亚辉

（中国运载火箭技术研究院，北京，100076）

0 引 言

返回式滑翔飞行器是指从不同轨道高度返回大气层后以滑翔飞行为主要飞行模式的飞行器的泛称。返回式滑翔飞行器的最小航程设计可以使得其落区范围能同时覆盖远距离和近距离区域，实现返回落区的大范围调节和控制。

目前关于最小航程影响因素的研究文献较少，一般是通过滑翔段能量管理实现纵平面内的大小航程调节[1,2]，也有基于空间机动模式下的最大横程再入轨迹设计[3]以及最小射程调节[4]，但关于飞行器最小航程的影响因素及其分析研究，在现有文献中很少见到。本文以类 CAV-H返回式滑翔飞行器为对象进行建模仿真，通过轨迹优化的方法实现最小航程，据此对最小航程轨迹优化中的初始状态、终端终态、质量规模、约束条件等影响因素进行了仿真分析，得到相关结论。

1 模型的建立

1.1 运动学模型

建立飞行器动力学模型如下[5,6]：

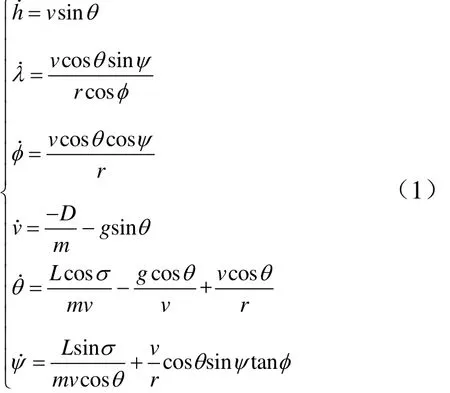
文中“航程”定义为飞行器在空间中运动时起始位置质心在球面的投影点至当前位置质心在球面的投影点构成的射程角所对应的球面大圆弧距离。

1.2 气动特性

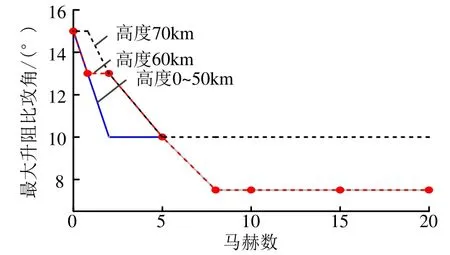
图1 最大升阻比攻角随高度变化曲线Fig.1 Change Curve of the Best Attack Angle with Height

由图1可知，随着返回式滑翔飞行器马赫数增高，最大升阻比攻角逐渐降低；高度越高，最大升阻比攻角越大。临近空间中低空条件下高超声速飞行最大升阻比攻角大致在 7.5~10°之间获得。本结论可用于后文的仿真结果分析。

1.3 飞行过程约束条件

式中 K为常数；Rd为驻点曲率半径；上标均与飞行器外形或材料有关；为当前高度下的大气密度；为标准海平面的大气密度；为当前飞行时刻；为环绕速度。

2 最小航程轨迹优化原理

通过轨迹优化方法，可得到返回式滑翔飞行器的三维空间最小航程轨迹。轨迹优化的原理如下。

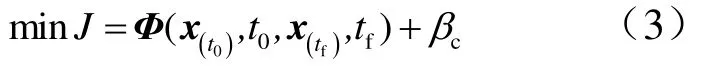
轨迹优化过程中，先用伪谱法[9]进行离散化处理，将最优控制问题转化为受到上述代数约束的非线性规划参数优化问题，再用成熟的序列二次规划法[10]进行寻优求解，得到最优轨迹。

3 最小航程影响因素仿真与分析

3.1 影响因素及仿真条件

返回式滑翔飞行器的初始状态信息，飞行器质量信息，以及滑翔末端的着陆需求信息等，构成了最小航程空间轨迹优化的主要影响因素。

以这些待优化变量为设计对象进行仿真，在标称状态值的基础上，对其量值施加上下偏差作为输入量，探究这些待优化变量对飞行器最小航程的影响。

标称状态仿真条件：初始飞行高度100 km、初始飞行速度 7200 m/s、初始倾角 0°、初始飞行航向角90°；末端飞行高度30 km、末端飞行速度3500 m/s、末端返回航向角360°；飞行器质量907 kg。

3.2 初始状态对最小航程轨迹优化的影响

3.2.1 初始飞行高度的影响

不同初始高度对最小航程空间轨迹的优化结果产生不同影响，按高度值逐渐下降进行仿真。在初始飞行速度7200 m/s、初始倾角0°条件下空间轨迹如图2所示。

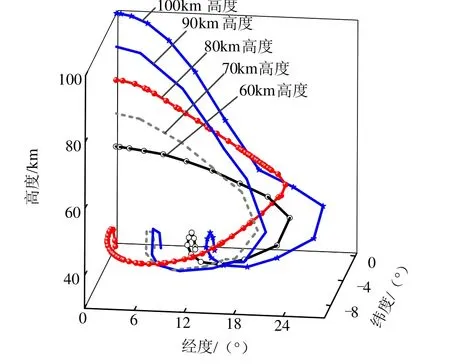
图2 初始高度下降对最小航程空间轨迹的影响Fig.2 Impact of Initial Height Decline in Trajectory Optimization

由图2可以看出，随着初始高度的下降，返回式滑翔飞行器的最小航程逐渐变小；但是随着高度继续下降，其最小航程反而逐渐增大。可知，适中的初始高度（80 km）有利于实现最小航程甚至返回离轨原点在球面投影点。在最佳高度下，可以得到为实现最小航程所需的控制曲线，如图3所示。

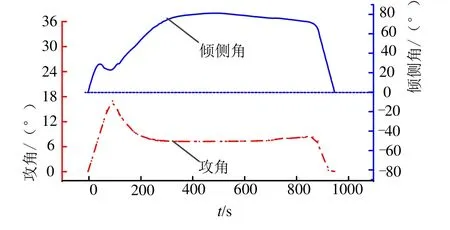
图3 最佳高度下的最小航程控制曲线Fig.3 Control Curve of Minimum Range with the Best Height

由图3可知，控制量曲线较为光滑，有利于控制系统的实现；且飞行器大部分时间以8~9°攻角飞行，与1.2节气动特性对比可表明，为了实现最小航程，飞行器需要保持最大升阻比攻角做三维空间机动飞行。

3.2.2 初始飞行速度的影响

初始速度对最小航程空间轨迹的影响如图4所示。

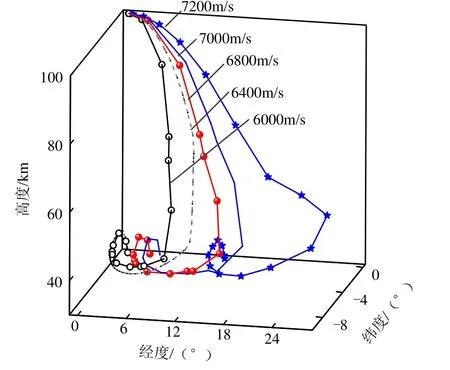
图4 初始速度对最小航程空间轨迹的影响Fig.4 Impact of Initial Velocity in Trajectory Optimization

由图4可知，初始速度对最小航程轨迹优化结果的影响较为单调（在一定变化范围内），随着初始速度的下降，最小航程不断降低。同时随着初始速度的下降，最小航程越来越接近于0。

3.2.3 初始倾角的影响

初始倾角对最小航程轨迹优化结果的影响较大，由于返回式滑翔飞行器一般不会“弹出”大气层，文中只取负值倾角0~-20°，仿真结果如图5所示。

由图5可知，随着初始倾角的减小，最小航程也不断减小，但减小的幅度越来越弱。所以在追求航程最小的同时，为了获得较大的参数调整效益，初始倾角可取小量负值（如-5°）。

同时，不同初始倾角条件下的热流密度约束情况如图6所示。由图6可知，虽然初始倾角减小有利于实现最小航程，但是热流密度峰值也因此增加、且热流峰值提前到来。从这个角度考虑，初始倾角也应该取小量负值。

图6 不同初始倾角下最小航程轨迹的热流约束情况Fig.6 Thermal Flow with Different Initial Bank Angle

3.2.4 初始航向角的影响

初始航向角对最小航程轨迹的形态和最小航程量值都有较大影响，仿真结果如图7所示。

图7 不同初始航向角下最小航程空间轨迹在水平面的投影Fig.7 Trajectories in the Horizontal Plane with Different Initial Heading Angles

由图7可知，初始航向角为90°且朝向目标方向时的标称状态下获得的航程比较适中；当初始航向角偏离标称值至 67.5°时可减小航程；但当初始航向角进一步偏离标称值至45°时，航程反而加大。这是由于标称状态下，飞行器在初始时间段内处于高空稀薄大气层中，无法通过气动控制实现大空域机动，这样飞行器沿初始航向方向进行滑翔飞行的距离较大，以至于无法完全实现绕弯返回；而在初始航向偏离标称航向较大情况下，则会导致横向滑翔飞行的距离较大，为了做到横向回归，需要进行大范围机动，这样会消耗能量，以至于无法兼顾缩小航程。

3.3 末端状态对最小航程轨迹优化的影响

在所有的末端状态中，末端航向角（返回角）对最小航程轨迹的影响最大，如图8所示。由图8可知，初始航向角相同时，针对不同的返回任务和场地需求，需要合理地选择返回角。

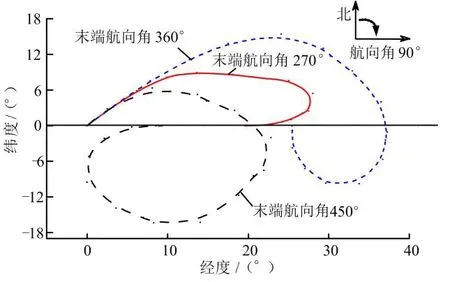
图8 不同末端返回角下最小航程空间轨迹在水平面的投影Fig.8 Trajectories in the Horizontal Plane with Different End-return Angles

关于末端高度和速度的其他仿真可以得到结论：适中的滑翔终端高度（30 km）有利于最小航程在工程中的实现；滑翔终端高度较高（40 km）时，由于整个飞行阶段空气相对稀薄，为了实现最小航程，飞行器大部分处于转弯状态中，转弯半径较大，且长期处于极限过载状态，对飞行器机体结构不利；滑翔终端高度太低（20 km）时，由于空气稠密，飞行器动压和热流密度峰值过大，因此不利于工程实现。

3.4 飞行器质量对最小航程轨迹优化的影响

飞行器质量对最小航程轨迹优化的影响如图9所示。

图9 不同质量飞行器的最小航程Fig.9 Minimum Range Curve with Different Mass

由图9可知，适当增加飞行器质量和减轻飞行器质量有利于实现最小航程。这是由于：a）较小质量下，飞行器机动能力更强，基本以过载上限值飞行，且能较早达到过载上限值，从而能够获得最小航程；b）质量增加时，由式（1），升重比下降，弹道倾角下降较快，这样飞行距离较近，也可获得最小航程。结果表明，质量907 kg以上时航程明显减小，侧面说明美国CAV-H飞行器质量数据选取907 kg可能有利于其维持较大射程。

3.5 飞行约束条件对最小航程轨迹优化的影响

飞行过程中的法向过载等飞行约束条件，会对最小航程轨迹的形态和量值产生较大影响，如图10所示。

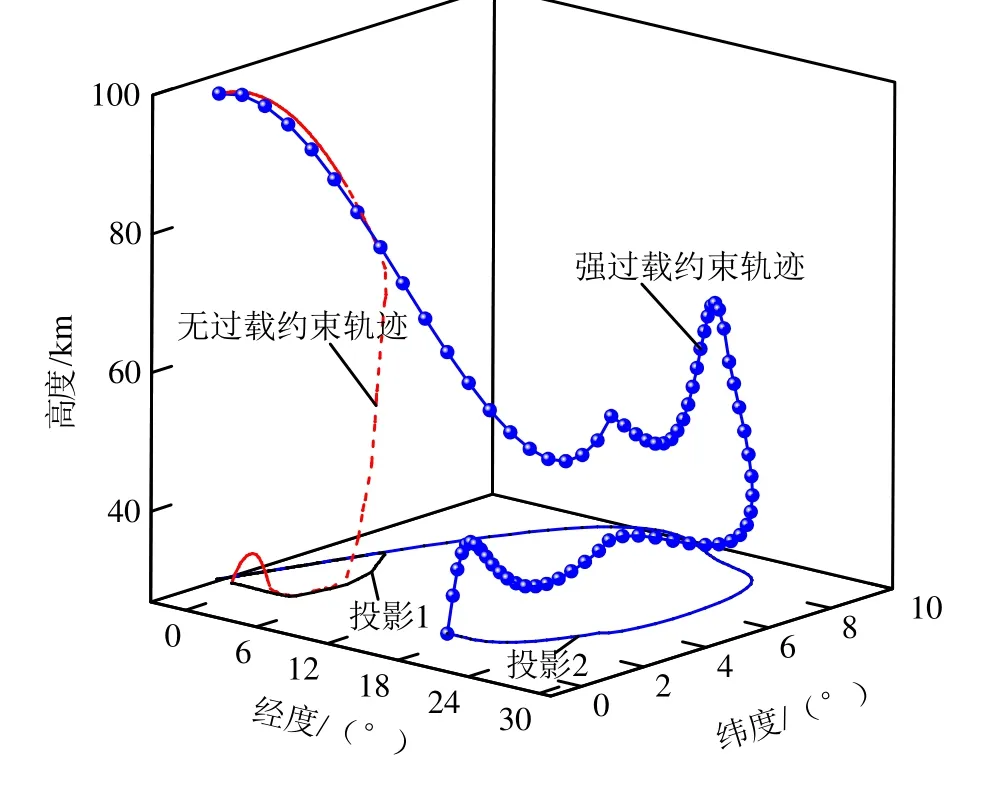
图10 不同过载约束下飞行器最小航程空间轨迹Fig.10 Trajectories with Different Overloading Constraints

由图10可知，在过载等强约束条件下，返回式滑翔飞行器的空间轨迹普遍存在绕弯半径偏大、返回更困难的现象。所以放宽约束条件有利于最小航程实现。

4 结 论

本文以类CAV-H返回式滑翔飞行器为研究对象，建立空间运动的坐标体系和运动学模型，给出法向过载、热流密度、动压等飞行约束条件，通过伪谱法和序列二次规划等方法进行轨迹优化，实现最小航程。以此为基础对最小航程轨迹优化中的初始状态、终端终态、质量规模、约束条件等影响因素进行了仿真分析，得到如下相关结论：a）适中的初始高度有利于实现最小航程甚至返回离轨原点；b）为了实现最小航程，飞行器需要保持最大升阻比攻角做三维空间机动飞行；c）适当减小初始速度能获得比较可观的最小航程；d）初始倾角可取小量负值，能在高效获得航程最小的同时兼顾热流密度；e）初始航向角适当偏离标称航向时，有利于获得最小航程；f）为了实现最小航程，在不同条件下需要合理地选择返回角/末端航向角；g）适中的滑翔终端高度有利于实现最小航程；h）适当增加或减轻飞行器质量有利于实现最小航程；i）放宽约束条件有利于最小航程的实现。