基于多分离剖面的航天器质心优化技术

张 群，杨 勇，杨自鹏，唐 颀，刘宇哲

(北京宇航系统工程研究所，北京，100076)

0 引 言

近年来，微纳卫星成为火箭发射的一个热门市场，为降低发射成本，一箭多星组合发射是商业微卫星发射的最优途径。升级版“太空摆渡车”的成功首飞，标志着中国上面级在多星部署技术瓶颈方面取得了新的突破，这一突破将有效满足中国的卫星市场发射需求，全面提升中国一次发射部署不同轨道及星座组网部署能力。

由于多星部署上面级组合发射的卫星尺寸规模、轨道高度、姿态要求各异，在多星部署过程中，不仅要进行多次变轨，根据不同的任务还要进行多次姿态机动，因此在释放掉一个或几个有效载荷后，其质心位置与转动惯量矩阵会发生较大变化。质心位置变化导致主发动机推力不再经过质心，姿控发动机产生的相对于质心的力矩也发生变化。以上面级为例，当质心偏离原主轴线时，姿控系统工作以稳定姿态，推进剂耗量将增加。以某型上面级飞行为例，假设质心横移增大1 mm，需要至少增加姿控推进剂用量为3.45 kg，若增大10 mm，则至少要增加34.50 kg 姿控推进剂。当质心突变量超出姿态控制能力时，将导致上面级姿态失控。由此可见，对于多星部署的上面级，基于分离剖面去优化箭体质心对飞行姿态控制意义重大。

1 多星质心优化研究现状

针对多星部署质心优化控制问题，国内外做了深入研究。Djerassi[1]研究了在运动中分离和捕获质量的变质量系统，并与传统的方法进行对比，得出只要在排除或捕获质量过程中作用在系统上的力已知，则可以用一个力来代替的结论；Reeves[2]针对利用反作用力来控制的系统，分析了推进剂的不断消耗对操作条件及飞行器设计指标的影响；Waishek等[3]研究了液体推进剂消耗对飞行器时变惯性特性的影响；吕红剑等[4]分析了质心漂移给空间飞行器姿态稳定控制带来的影响，计算出保证姿态稳定所允许的最大质心漂移量。

从国内外研究可见，大部分成果均集中于研究最优姿态控制方法，来解决飞行过程中质量特性变化引起的姿态稳定问题，这种方法对控制系统要求高；而对于通过分离剖面的质心设计来优化全箭质心突变的方法，国内外尚无深入研究技术成果。本文从复杂空间飞行器总体技术出发，提出航天器质心优化设计方法，以期降低多星部署上面级姿态控制系统的难度。

2 质心优化方法

对于多星部署上面级而言，因卫星规模和分离轨道需求差异，在结构布局上需要综合考虑分离时序和对上面级的横向质心影响。根据上面级姿控能力，全飞行周期内各分离剖面横向质心需控制在 Ф8 mm范围内。为达到这一指标且姿控耗量最低，需确定多星布局的质心优化方案。

为此，本文提出了一种基于分离剖面的航天器质心优化方法，即根据卫星结构规模和任务特性，优化上面级组合体的结构布局，再结合分离时序划定分离剖面，按剖面求解质量和质心位置，再根据质量局部修正来控制上面级质量及质心。

2.1 总体构型优化

总体构型如图1所示。

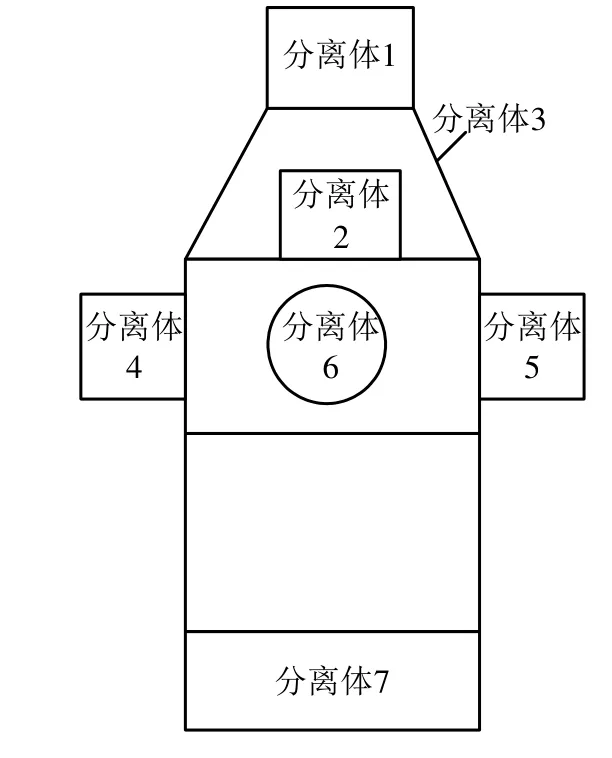
图1 总体构型Fig.1 Denotation of Combination

航天器构型设计是航天器系统设计的重要内容之一，是结构设计的基础和前提[5]。搭载“太空摆渡车”发射的7颗卫星规模迥异，质量最轻的仅23 kg，最重的达3000 kg。为减小横向质心偏移量，在总体构型设计上，需合理优化布局。

为使结构紧凑、受力合理，结构布局要有利于减小载荷和有利于力的传递[6]，优先布局主星和规模较大的结构部段，以保证箭体具有较大的静稳定裕度；其次根据卫星分离释放的时序布局卫星的具体位置；最后，对称布局尺寸规模较小的卫星。

2.2 分离剖面划分

分离剖面的划分需综合考虑飞行时序和结构布局。上面级一箭七星结构布局复杂，包括了运载器最典型的两种布局方案，串联和并联复合的结构布局方案，复杂布局和分离方案可以衍生出不同的分离面，为便于箭体综合质心设计优化，分离剖面以分离动作为标志，各卫星的分离方式见图2。

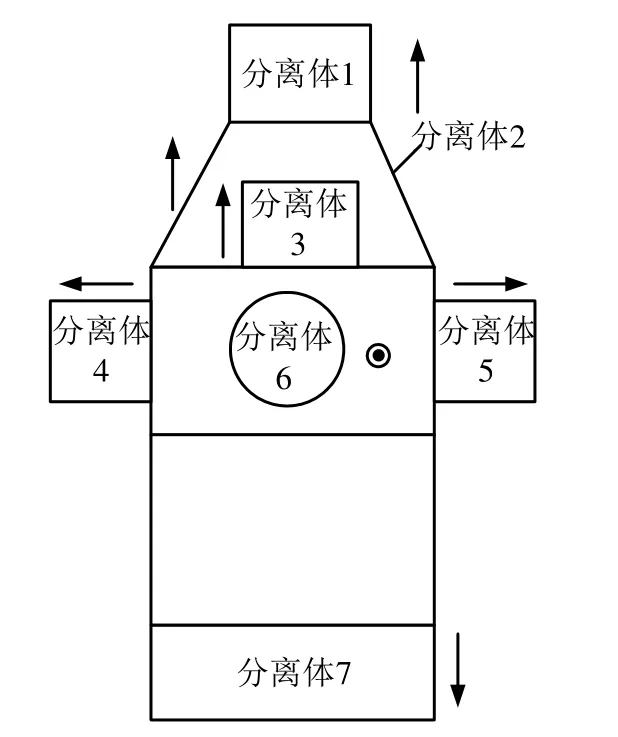
图2 分离方式示意Fig.2 Schematic Diagram of Separation Scheme

以太空摆渡车为例，组合体共包含7个分离载荷、1个上面级本体、5个分离剖面。此外，作为载荷组合体，与基础级火箭分离同样需要保证组合体的质量特性。因此，根据飞行任务剖面和姿、轨控控制精度要求，载荷组合体共划分为6个分离剖面，如图3所示。

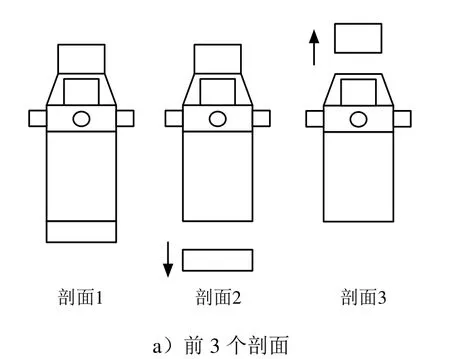
图3 分离剖面Fig.3 Plane of Separation

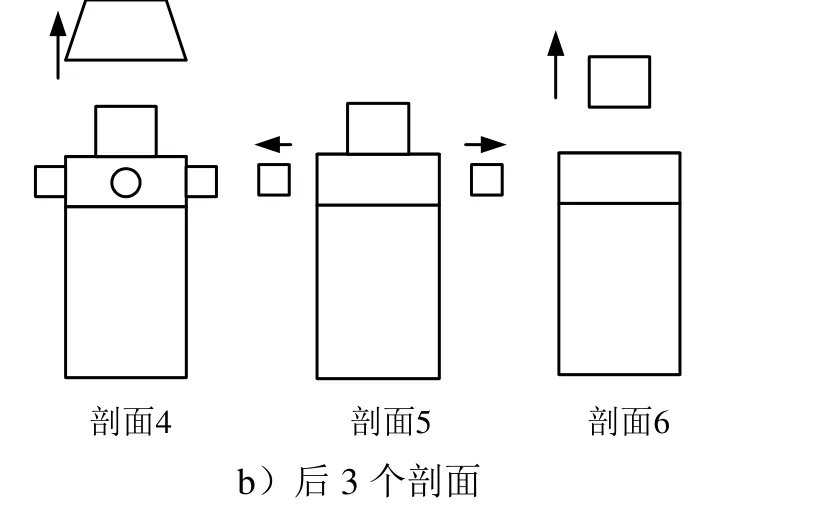
续图3

2.3 组合体质心优化

2.3.1 质心偏斜计算

对图2所示太空摆渡车组合体，根据6个分离剖面划分出 8个质量单元，分别为分离体 1~7、本体，然后对各质量单元质测，对各分离剖面推进剂剩余情况估算、质量特性局部修正，最终通过质心配平计算得出最终全箭质量特性。

式中mi为第i个质量单元的质量；yi为第i个质量单元横向质心的Y向坐标；zi为第i个质量单元横向质心的Z向坐标；y0，z0分别为全箭质心位置的横向坐标。

分别对分离体1~7进行质测，得出各质量单元的质量和横向质心，根据图3确定的6个分离剖面，按照式（1）所示质心偏斜计算方法及结构安装布局，计算出在未配平状态下各分离剖面的结构质量级质心横向偏移量，最终计算结果如表1所示。

2.3.2 质心调整方案

假设偏心点 A位于Ⅲ象限，配平装置最佳的安装位置为偏心点关于原点O对称方向，即Ⅰ偏Ⅱ象限线。如图4所示，A点为偏心点，B点为配平装置安装点，安装点位于上面级组合仪器舱壳体外表面，壳体直径为Ф，由此可得配平装置质量为mp。

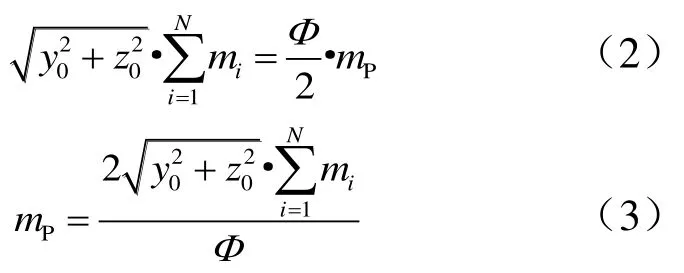
式中mp为需要的配重块质量。

图4 质心配平方案Fig.4 Principle of Keeping Centroid Balance

2.3.3 多剖面综合质心调整方案

对单个分离剖面配平时，该剖面状态下组合体偏心距L。因此该状态理想配重量所产生的偏心距应为-L，若容许偏差为 ΔL，则配重量所产生的偏心距为-L+ΔL，其中ΔL=。因此，综合分析每个分离剖面，允许配重产生的偏心距如图5所示。

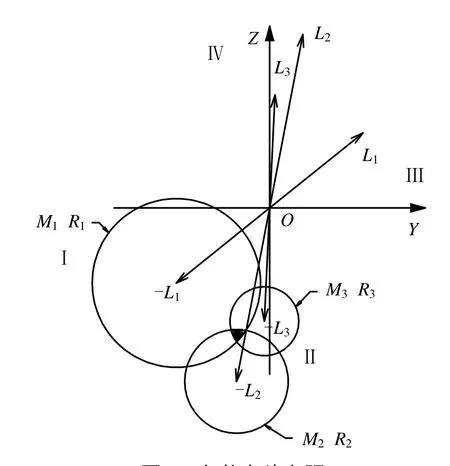
图5 各状态偏心距Fig.5 Eccentric Arm

由图5可知，如果配重偏心距存在交集，则矢端在阴影部分的偏心矩所对应的配重量及配重位置可以同时满足所有分离剖面的质心偏差要求。假设进而可得配重块安装位置为方位角，配重块质量为，其中D为配重块安装直径。

当各分离剖面偏心距无重叠部分时，表明配重后无法同时满足所有分离剖面的质心偏差控制要求，因此，需根据不同原则选取不同的配重方案，如图6所示。

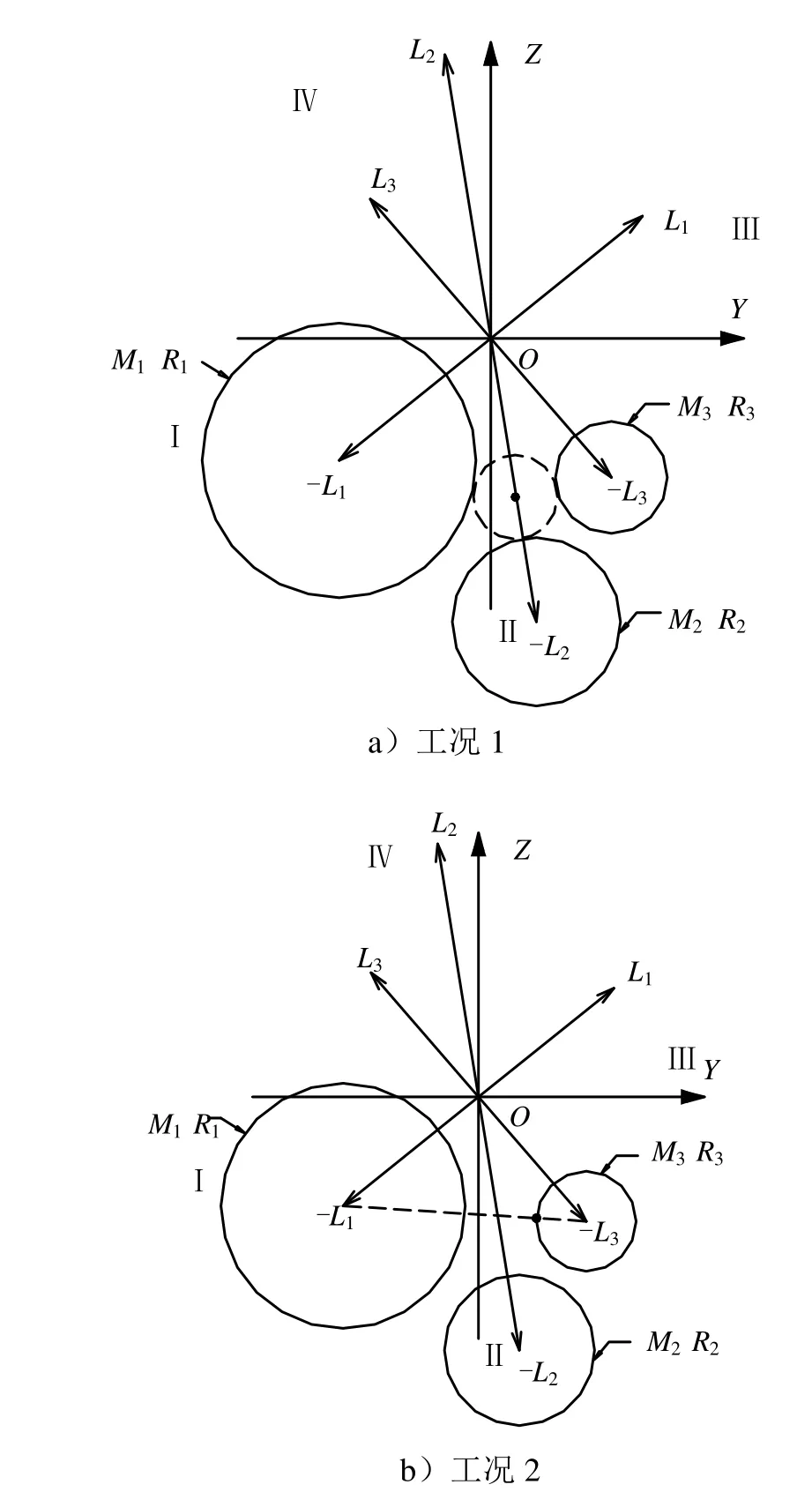
图6 各分离剖面偏心距图Fig.6 Eccentric Arm of Separation Planes

3 误差修正及实施效果

3.1 质量误差

质量误差可表示为

3.2 质心误差

质心误差可表示为

3.3 实施效果

各剖面质量和质心数据如表2所示。

表2 各剖面质量和质心数据Tab.2 Mass and Centroid of Separation Planes

由质心偏斜计算和多剖面质心综合调整方案，经误差修正后，对于具有7个分离剖面的箭体，在优先考虑箭体姿态控制能力前提下，对关键剖面和组合体进行质心调整，最终得出各飞行剖面的质心偏移数据。

4 结束语

本文通过总结上面级组合体全箭质量特性控制经验，提出一箭多星多分离剖面的上面级组合体质量特性控制方法，经优化计算，全飞行周期内，各剖面虽未达到0 mm质心偏移，但组合体最终质量和各剖面质心偏斜数据均得到了保证，最大剖面发生在剖面6，质心横移为 2.29 mm，若包络系统误差，最大横移为3.04 mm，满足最初提出的±3.5 mm制表要求。这一方法为实现多载荷分离技术的高精度轨道、姿态控制，提供了准确的被控对象质量特性参数，为航天器各飞行剖面精确入轨和安全分离提供了有效保障和具体措施。