一类立体几何试题的模式化解法分析——以2019年全国卷Ⅰ试题为例

云南

在历年高考数学选择题与填空题中总会设置一道以立体几何知识为背景的压轴题，球的切接问题、点到平面的距离和线面角等知识是考查的热点.垂直关系是命制这一类立体几何试题的核心要素，同时也是解答该类问题的关键点和突破口.如何抓住垂直关系合理构建模型是正确解答的前提，文章以2019年全国卷Ⅰ试题为例谈如何用特殊值(位置)法、分析法和补体法等模式化方法解答该类问题.

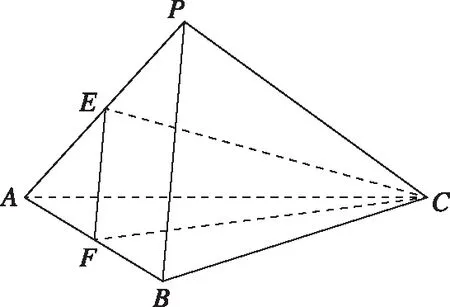
例1.(2019·全国卷Ⅰ理·12)已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF=90°，则球O的体积为

( )

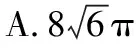
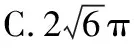
试题分析：从知识的角度看，本题考查多面体外接球体积的求法，首先要根据已知条件构建几何模型，弄清楚多面体的边角关系，其次找到球心并求出半径，最后利用球的体积公式进行计算；从思想方法的角度分析，本题重点考查转化与化归的数学思想，如何将已知多面体的几何关系转化为与球的半径有关的几何关系是解题的关键；从考查素养的角度分析，重点考查数学抽象、逻辑推理和数学建模等核心素养，以考查空间想象能力为切入点，考查数学运算能力.

方法一、特殊值(位置)法

鉴于该类问题多以选择题和填空题的形式出现，可以在符合题目要求的前提下，将几何关系进行合理的特殊化，以简化计算过程并快速得出答案.

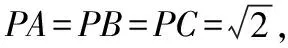
解法评析：采用特殊位置或者特殊值法具有操作简单而且有利于简化推理与计算过程的作用，从而快速得出答案，是高效解答选择题和填空题的有力武器之一，但不是所有的题目都能特殊化，要具体问题具体分析，比如例1假设了特殊位置后，要有意识地检验一下是否符合题设条件∠CEF=90°.

方法二、分析法

分析法指的是用常规方法解题，即立足于已知条件，着眼于解题目标，从目标倒推问题的解决过程.如例1要计算外接球的体积，只需要确定外接球的半径，而要求出外接球的半径，首先必须确定球心位置，而确定球心位置必须先弄清楚三棱锥的边角关系，经历以上的分析转化过程可知问题的关键在于探究三棱锥的边角关系和几何特征，按照这个解题思路问题可迎刃而解.

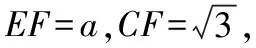
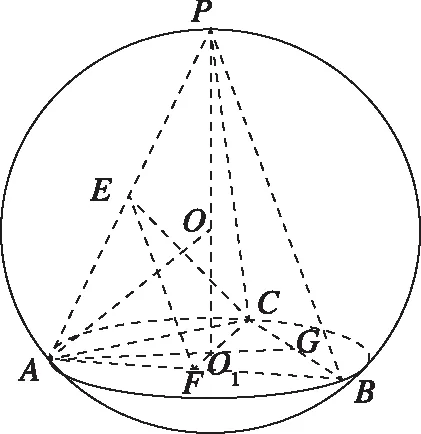
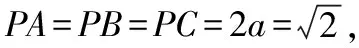
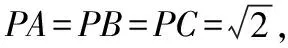
解法评析：思路2与思路1的出发点不同，思路2先探究PA，PB，PC之间的几何关系(定性)，即先证明PA⊥BC，PB⊥AC，PC⊥AB，再由∠CEF=90°得出三条侧棱PA,PB,PC两两互相垂直；思路1则是先从边的长度(定量)的角度出发，但是殊途同归，效果一样.

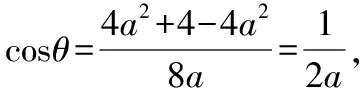
解法评析：思路3没有直接构造出多面体与外接球的几何模型，而是先着眼于探究三棱锥的几何特征，处理方法和思路1相似，根据定量计算得出三条棱两两互相垂直的定性关系，借助正方体模型顺利解题.

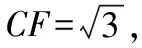
解法评析：思路4与思路3处理方法一样，只是着眼点不一样，都是将空间几何问题合理转化为平面几何问题，从而利用余弦定理得出结论.

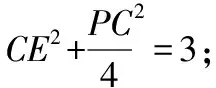
解法评析：思路5从三棱锥的定量计算出发，利用平行四边形“对角线的平方和等于四条边的平方和”这一重要性质得出4CE2=8+PC2，充分体现了转化与化归数学思想的实用性，也说明将立体几何平面化是处理多面体边角关系的有效途径.

方法三、补体法

补体法是解决该类问题的高效方法，根据柱体进行适当切割可得锥体这一几何特征，往往可以给锥体找一个合适的载体即柱体，将棱锥放置于特殊的棱柱中，若锥体的顶点与柱体的顶点重合，那么锥体的外接球即为柱体的外接球，由于直四棱柱外接球的直径即为体对角线，所以经过以上的转化过程即可将复杂问题简单化.

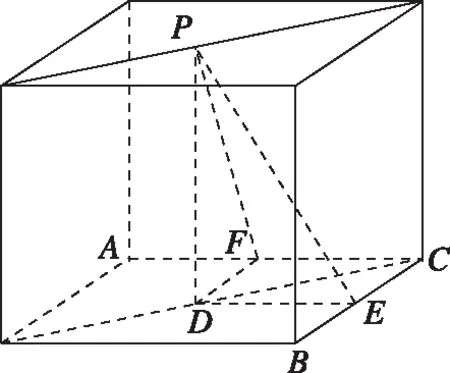
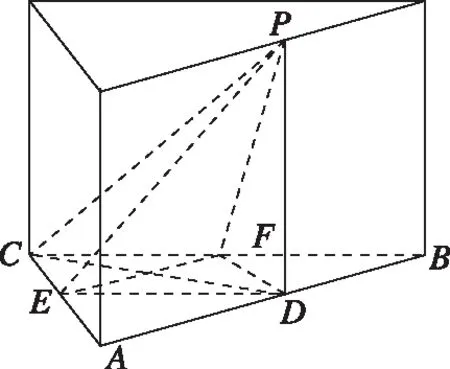
思路1.如下图所示，可将该正三棱锥放置于底面是菱形且∠CAB=60°的直四棱柱中，当然也可以是底面为正三角形的直三棱柱中，处理思路可参照方法二中的思路1与思路2.

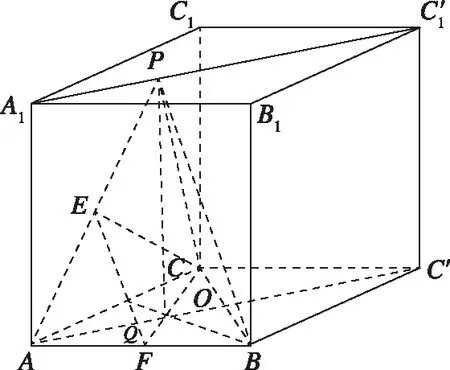
思路2.如下图所示，可将该正三棱锥放置于正方体中，当然也可以是底面为等腰直角三角形的直三棱柱中，处理思路与方法一的特殊位置法一致.

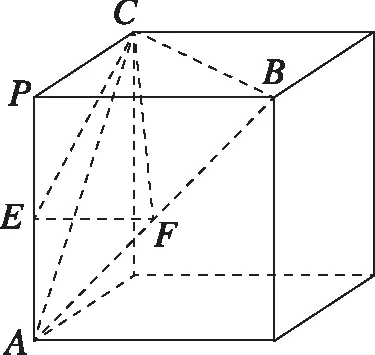
方法四、向量法

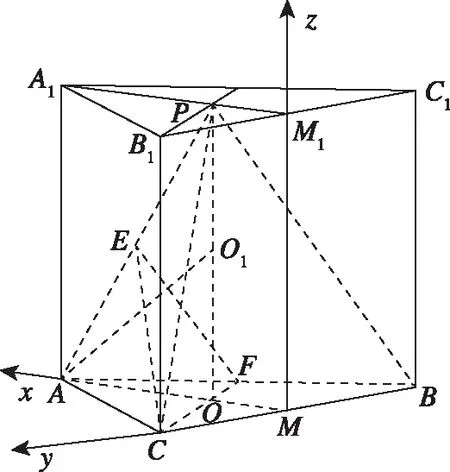
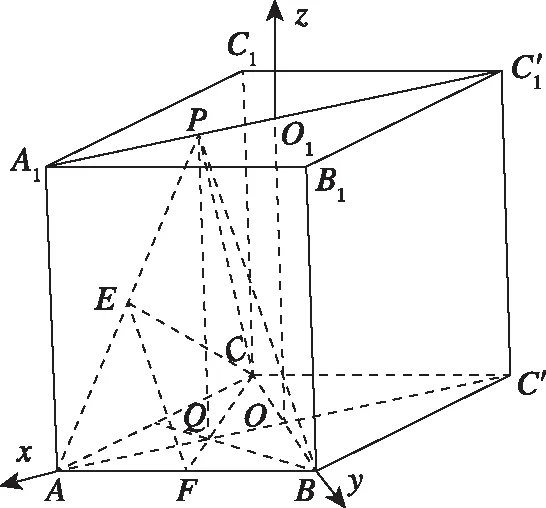
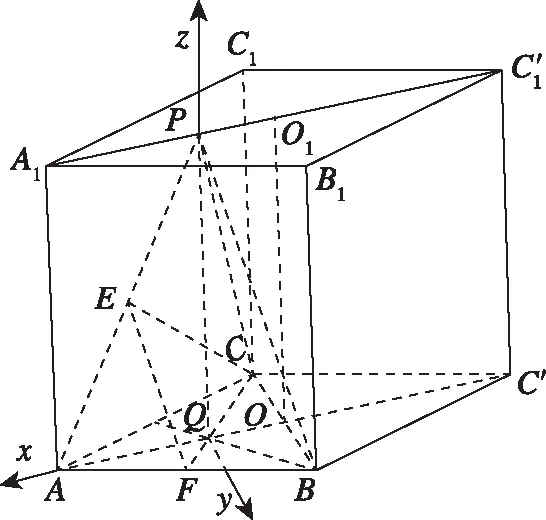
向量是解决立体几何问题的有力工具，抓住垂直这一关键几何特征并能建立恰当的空间直角坐标系，用好向量坐标运算能够有效降低题目的抽象性，从定量计算结果论证空间点线面的几何关系.

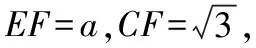
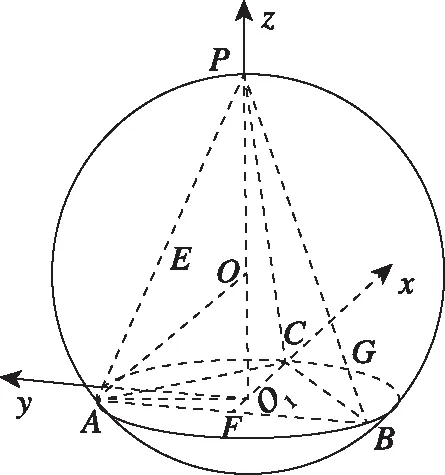
思路2.如下图，同一个几何体模型中，选择不同角度的垂直关系可以建立不同的空间直角坐标系，但是运算的方法和过程基本一样.

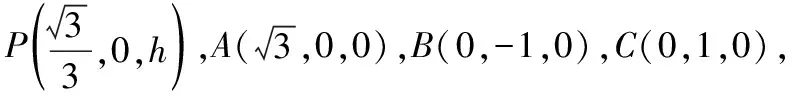
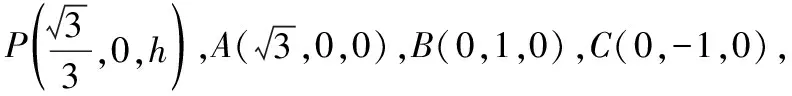
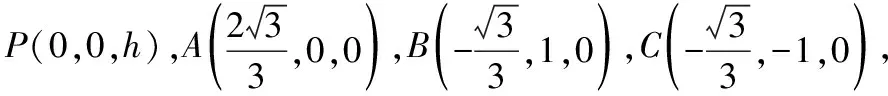
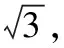
1.特殊值(位置)法

2.分析法

3.补体法

例2仍然可以用补体的思想来解答，既可以将其补体为解法1思路1中所示的长方体，也可以将其补为解法1思路2和思路3所示的直棱柱，解法同上.

4.向量法

例2中存在垂直这一特殊的几何关系，所以还可以通过建立空间直角坐标系求解，但是由于题目本身难度不大，选用向量法会显得有些小题大做，但是如果单从解题方法的角度来看，向量法也不失为一种好方法，所建的空间直角坐标系可参考下面两个图，具体解答过程略.

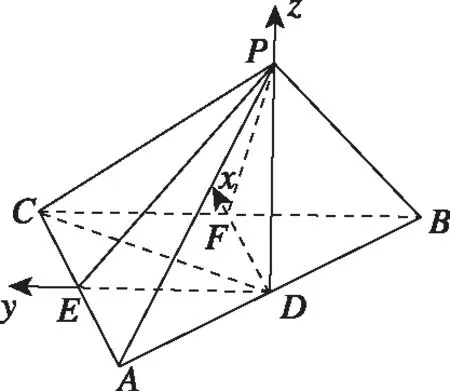
通过对以上两个典型试题从特殊值(位置)法、分析法、补体法与向量法等四个常用方法进行分析可以看出，解决该类以垂直关系为关键元素所命制的立体几何压轴题具有相对稳定的解题模式，而且方法各有所长，需要在平时的学习过程中不断总结，积极探索，以期能在解决实际问题的过程中以最短时间选择最优的解题方法实现正确解答.