稳定中创新，创新中提升——2019年浙江高考数学命题特点

浙江

2018年浙江高考数学卷比较，2019年高考数学命题呈现出命题的稳定性，其显著特点为“突出四基”——基本运算成为学生痛点，“重视素养”——核心素养的考查呈现难度提升，“风格简洁”——题干信息量丰富，设问角度新颖.新特点对2020年高考数学复习的启示是教学中要更加重视“数学基础的训练”“核心素养的渗透”“变式教学的训练”和“思维痛点的消除”，在新的数学课程标准引领下，扎实地做新时代数学基础教育.

一、2019年与2018年浙江高考数学比较

1.内容比较

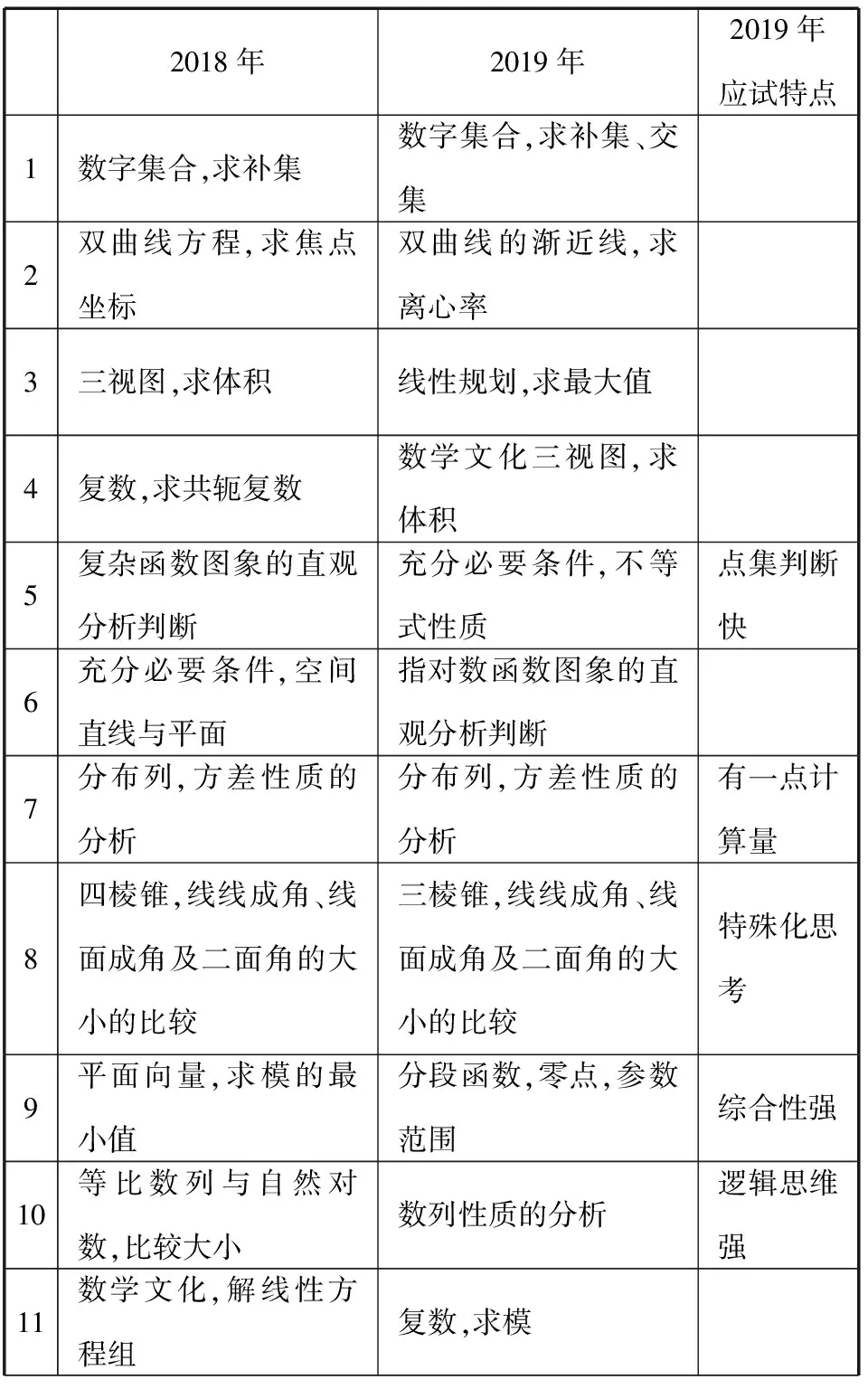
2018年2019年2019年应试特点1数字集合,求补集数字集合,求补集、交集2双曲线方程,求焦点坐标双曲线的渐近线,求离心率3三视图,求体积线性规划,求最大值4复数,求共轭复数数学文化三视图,求体积5复杂函数图象的直观分析判断充分必要条件,不等式性质点集判断快6充分必要条件,空间直线与平面指对数函数图象的直观分析判断7分布列,方差性质的分析分布列,方差性质的分析有一点计算量8四棱锥,线线成角、线面成角及二面角的大小的比较三棱锥,线线成角、线面成角及二面角的大小的比较特殊化思考9平面向量,求模的最小值分段函数,零点,参数范围综合性强10等比数列与自然对数,比较大小数列性质的分析逻辑思维强11数学文化,解线性方程组复数,求模

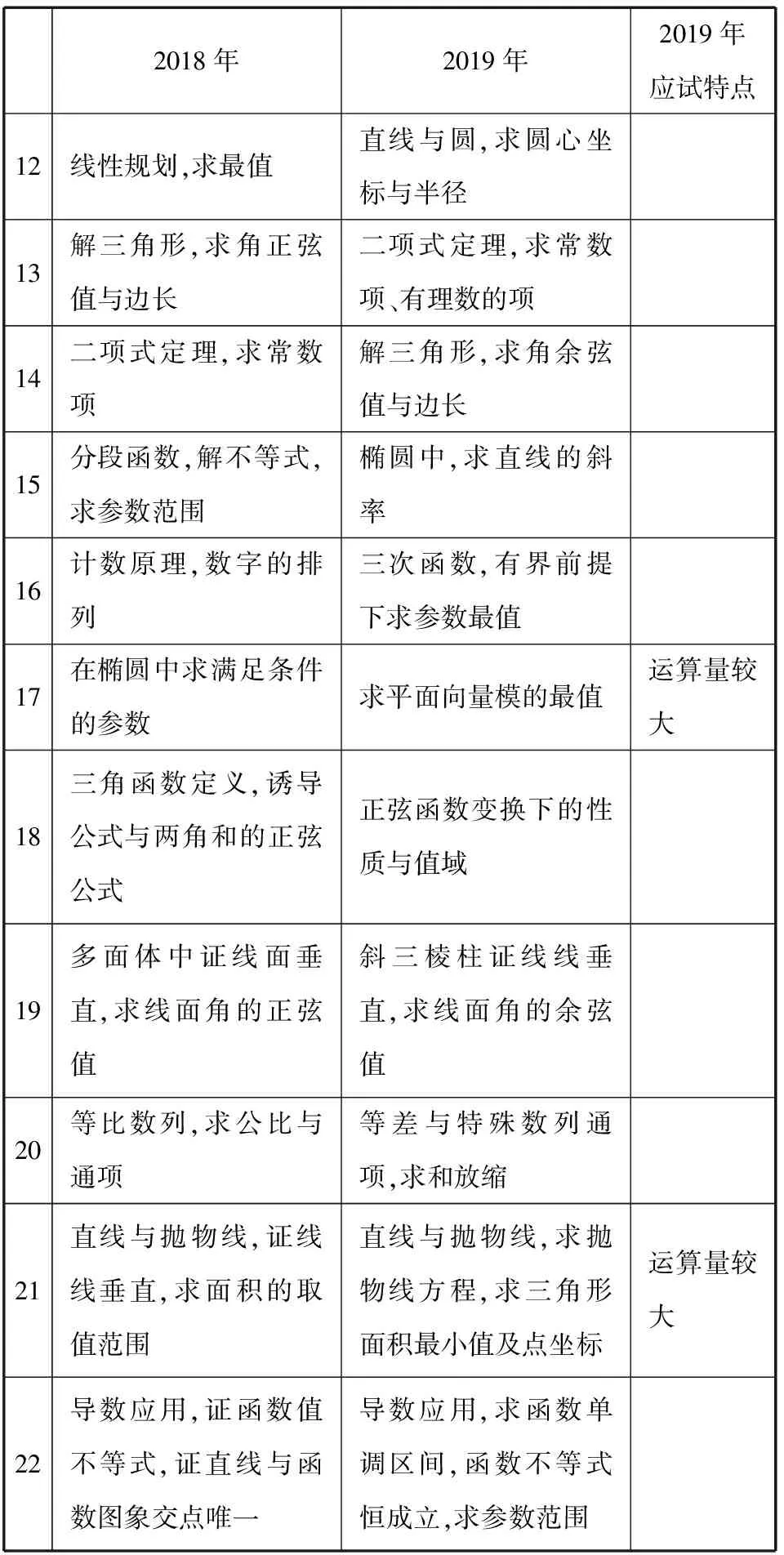
续表

从考查的主干内容上来看稳定优先，由上述对照可见变化不大，基础题保持高度一致，有创新亮点的题如第17题，在平面向量上显示亮点；第9，10题为难度较大的题，设计目的是要显示区分度；第16题考查函数不等式有解条件；第22题考查函数不等式恒成立时参数的范围.

2.2019年浙江高考数学命题的显著特点

(1)突出四基

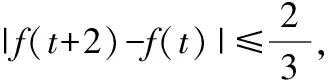
分析：在思考过程中蕴含了“绝对值的概念与意义”的基础知识，“运用乘法公式”的基本技能，“整体换元”“等价转化”“数形结合”等基本思想和“存在性、恒成立问题解决”的基本活动经验的综合，考生只有在真正意义上掌握了这“四基”，才能较好地解决此问题.

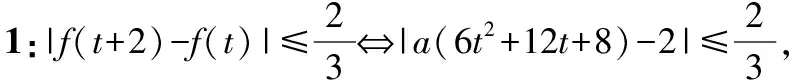
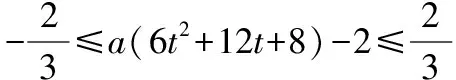
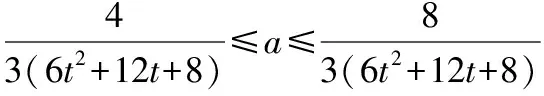
因为6t2+12t+8∈[2,+∞)，

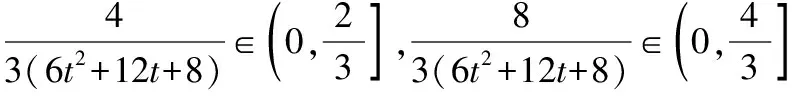
解析2：f(t+2)-f(t)=2a(3t2+6t+4)-2，令3t2+6t+4=m,m∈[1，+∞)，

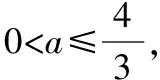
(2)重视素养

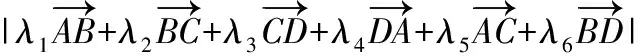
分析：以平面向量为背景，考查了考生是否具备核心素养：数学抽象(将具体的几何图形正方形和多个平面向量抽象为平面向量基本定理，用平面向量的基底描述问题本质)、数学建模(在众多平面向量中选取其中两个最特殊的向量作为研究问题的基底，然后建立模型解决向量问题)、逻辑推理(将所要求解的六个向量的线性式转化为两个基底向量的表达式，进行分析研究)、数学运算与数据分析(结合题设所给关于几个向量系数的选取条件，结合向量模长变化进行处理与确定)和直观想象(充分发挥平面向量作为数形结合典范的作用进行想象，确定问题答案)，考生只有具备这些核心素养，才能顺利解答，反过来，这个问题设计的亮点在于能够较好地考查考生的数学能力与素养，达到甄别和选拔人才的目的.

(3)风格简洁

浙江高考数学命题一直保持着“入口宽、起点低、解法活”的风格，2019年浙江高考数学命题见证了文章“2019年浙江高考数学考试说明解读新视角”中的预测，渗透“核心素养”，内容无变化，题型无变化，在三大方案中，仍然按方案二呈现“低起点高品位，简洁语内涵丰，强基础重主干”的特点，题目中最短阅读量只有10个字，最长阅读量也不会超过100个字，但是题干中信息量丰富，设问角度新颖.

( )

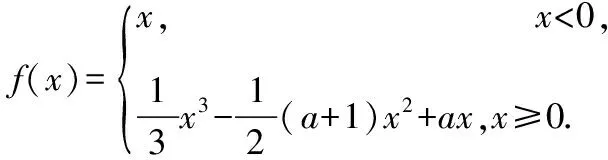
A.a<-1，b<0 B.a<-1，b>0

C.a>-1，b<0 D.a>-1，b>0

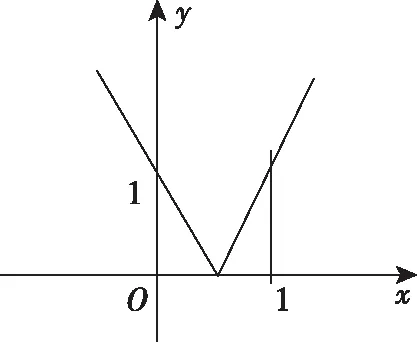
分析：本题涉及三次函数，分段函数、函数零点、方程求解、导数应用、双参数分析和数形结合分析等知识点，给应试者提供的思考空间很大，此题的解题思路很多.

二、新特点对2020年高考的影响

1.重视数学基础训练

浙江高考数学，数学基础何其重要！唯有数学基础扎实，才能有所作为；唯有数学基础扎实，才能谈数学方法.否则就如墙上的芦苇，头重脚轻根底浅，如山间的竹笋，嘴尖皮厚腹中空.数学复习中，教师要关注每一位学生的数学基础，由于小学和初中的数学基础薄弱对高中数学学习的影响极大，因此，每一位学生在高中的数学学习中，对初中和小学的数学知识点和解题方法欠缺的应及时补上，并记录在笔记本上，随时复习与记忆，要高度关注学生的数学运算，包括分数运算、繁分数运算和解各类方程(组)的运算，特别是含有参数的运算，运算训练的目标是会、准、快、简、优！高考数学应试时间只有两个小时，所以任何弱化运算能力培养的观点都是对学生的不负责任！

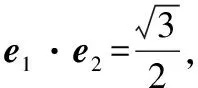
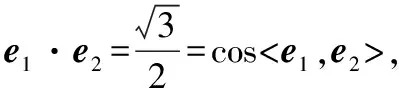
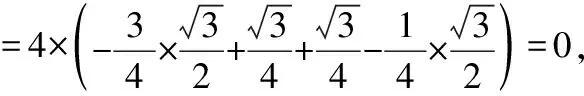
解读：这是一道涉及向量函数的基本运算的试题，许多学生过不了关有两个原因，一是向量函数本身的运算，只需要根据定义(*)；二是向量函数定义中向量夹角的变化对向量运算的影响(**)，这两处是学生运算出错较多的地方，如果对如此简单的向量基本运算都不重视，将如何应对高考数学平面向量问题呢？

2.重视核心素养渗透

2017年版《普通高中数学课程标准》已经明确数学教学要渗透“核心素养”，并给出了水平评价指标与案例，今后的高考数学题只会越来越强化这一点.特别是数据分析素养是数学教学的弱项，必须强化.

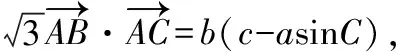
(Ⅰ)求角A的大小；

(Ⅱ)设b=c，N是△ABC所在平面上一点，且与点A分别位于直线BC的两侧，如图，若BN=4，CN=2，求四边形ABNC面积的最大值.

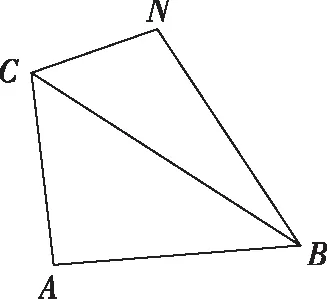
解析：

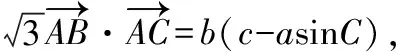
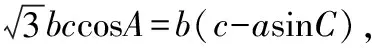
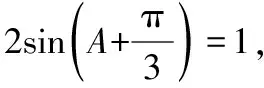
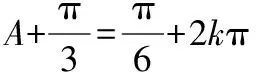
又a2=2b2，

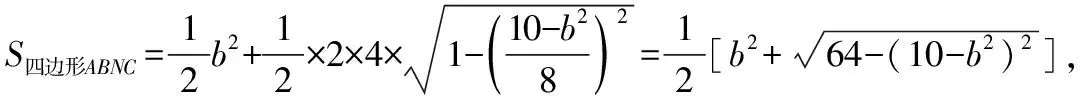
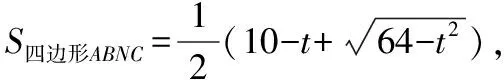
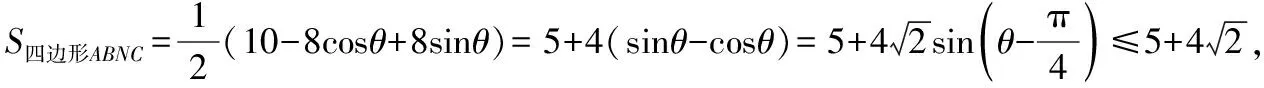
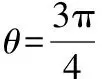
解读：

(1)第(Ⅰ)问中边角之间的灵活转化是求角A的关键，运用辅助角公式以及解三角方程是基本功；

(2)第(Ⅱ)问中如何选择变量建立关于面积的函数是解题关键，根据题设给定的边的关系以及对角A的确定，从而找到a2=2b2是一个关键点；

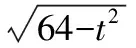
(5)最后借助辅助角公式，化简函数，利用正弦函数有界性求出函数最大值；

(6)此题求解中蕴含着数学建模、逻辑推理、数学运算和直观想象等数学核心素养.

3.重视变式教学训练

有效运用问题变式和解法变式是提升学生数学思维的重要途径，教学中不能只关注数学难题，而要多关注基础性试题对提升学生数学能力的作用.

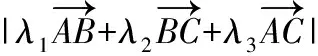
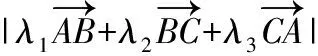
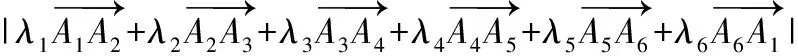
4.重视解除思维痛点

学生在数学学习过程中的痛点反映在“难题”的突破上，“运算力”的突破上，“基础”是否牢固上，“数学学习心理”是否优良上，“逻辑推理能力”是否形成上，“数学公式”是否记牢上，“数学解题目标意识”是否形成上，以及对“题目条件的解读”是否精准上等.

数学解题过程中遇到的痛点是由“错点”“漏点”与“智慧点缺失”所组成的一个问题，从已知信息出发，推出错误的结论，必然导致问题求解失败，这是错点；在求解过程中漏掉某一个条件的思考而形成的结论也是错误的，这是漏点；求解过程中需要一些智慧点才能实现问题的转化，而缺少这些智慧点就不能实现问题的突破.因此出现错点和漏点，以及缺少智慧点，共同构成解题失败的痛点.其中错点的“痛”是失败造成的痛；漏点的“痛”是遗憾不为造成的痛；而智慧点缺失的“痛”是激起奋进的痛.

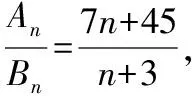
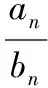
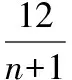
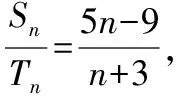
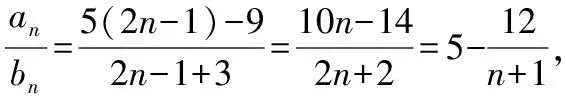
当n=1，2，3，5，11时，t=-1，1，2，3，4，所以符合题意的正整数t的个数是4.

解读：

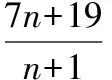
(4)等差数列中，通项、中项与前n项和之间的联系最为密切，这也是高中数学中应用的一个知识点.