核心素养导向下高考一轮复习策略探究——以圆锥曲线与方程章节为例

广东

随着基础教育课程改革的不断深入，学生学科基本素养的培养越来越为人们所关注，数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用过程中逐步形成和发展的.数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.数学高考一轮复习是数学高考复习中最重要的环节，如何将数学学科核心素养的培养和一轮复习有效结合，让一轮复习高效运行，是数学老师必须思考的问题.本文基于核心素养的导向，结合圆锥曲线章节探究数学高考一轮复习策略，以期提高复习教学效率.

很多数学老师认为核心素养是在高一高二的课堂中落地生根的，高三的一轮复习教会学生做题就可以了.因此造成了题海战术，学生一轮复习下来效果并不好.究其原因，这样的复习策略导致复习失去了数学培养的方向和目标，学生没能掌握数学学习与高考考查的本质.笔者基于核心素养的导向，结合圆锥曲线章节，探究数学高考一轮复习策略.

1 基于数学抽象核心素养，强化概念，整体把握

笔者认为圆锥曲线考查的最终落脚点是概念与计算.很多学生在做圆锥曲线的题目时，都卡在了概念的运用上.学生对概念不熟练，导致很多不难的题目变成了难题.

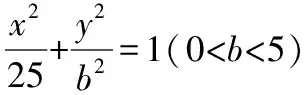
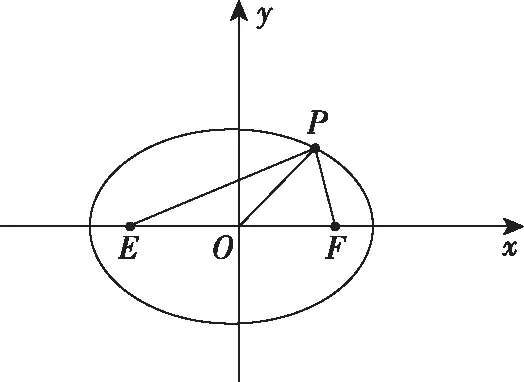
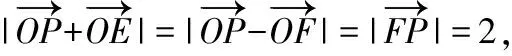
圆锥曲线在高考中会有一个12分的解答题，一般情况下这个题的第一问是围绕概念求圆锥曲线的标准方程.如果第一问做错，那么这个题基本上就得不到什么分.

【例2】已知圆A：x2+y2+2x-15=0，直线l过点B(1，0)且与x轴不重合，l交圆A于C，D两点，过点B作AC的平行线交AD于点E.

(1)求点E的轨迹方程；

(2)设点E的轨迹为曲线C1，直线l交C1于M，N两点，过B且与l垂直的直线与圆A交于P，Q两点，求四边形MPNQ面积的取值范围.

第一问是本题的关键，其本质就是对椭圆概念的考查.如果学生在复习过程中深度地把握了椭圆的概念，理解了椭圆的定义中有两个定点，然后椭圆上的点到两个定点之和是常数，那么学生就容易找到出发点解答，过程如下.

解析：(1)因为|AD|=|AC|，EB∥AC，所以∠EBD=∠ACD=∠ADC.

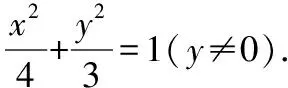
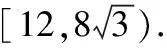
复习策略：数学抽象是指通过对数量关系与空间形式的抽象，得到数学研究对象的素养.在数学抽象的核心素养导向下，高三的学生在一轮复习中，对基本概念的复习不能像新课教学那样孤立复习，而是要整体把握，要从数量与数量的关系，图形与图形的关系中抽象出数学概念与概念之间的关系.如到两个定点距离之和为常数(大于两个定点之间的距离)能抽象出椭圆，定点为焦点，常数为2a；到两个定点距离之差的绝对值为常数(小于两个定点之间的距离)能抽象出双曲线，定点为焦点，常数为2a，等等.概念整体的把握可以使学生掌握概念的本质，清晰概念的内涵与外延.要多回归课本经典例题和习题，抽象出经典的圆锥曲线模型，如我们课本后面的习题就有两个通过中垂线转化线段长度的椭圆与双曲线的模型.另外还要加强转化思想，灵活使用定义，在椭圆与双曲线中到一个焦点的距离灵活转化为到另外一个焦点的距离；在抛物线中，到焦点与到准线距离的相互转化应用.

2 基于直观想象核心素养，贯穿数形结合数学思想

圆锥曲线是解析几何内容，解析几何是用代数方法研究几何对象之间的关系和性质的一门几何学分支.具有几何图形的直观性质，也具有代数的运算性质.因此在圆锥曲线的解答过程中，要充分利用图形的直观性.比如下面的这个例题，学生不但不会做，而且看答案都看不明白，因为当时答案中没有图象只有解答过程.

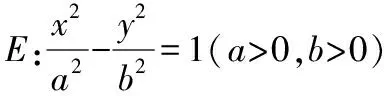
此题在解答的过程中，学生总觉得没有可能是两条的情况.解答时笔者给学生画了下面的两幅图，让学生从图形直观去分析.

在图1中，若|AB|=4b，根据双曲线的对称性，下方也可以画出一条直线l满足|AB|=4b；此时左支上则不存在满足条件的直线，得到：

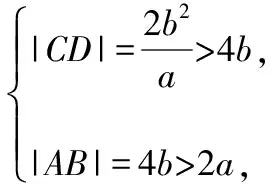
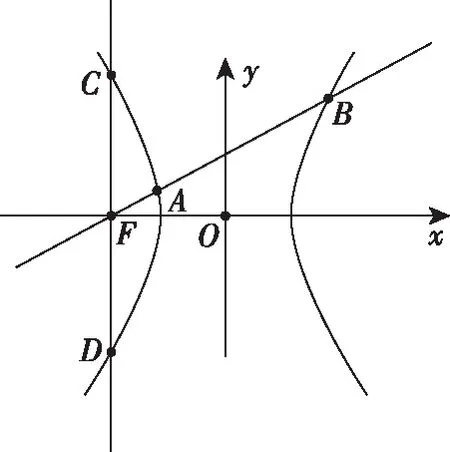
图1

在图2中，若|AB|=4b，根据双曲线的对称性，仍可以画出一条直线l满足|AB|=4b；此时左、右支上不存在满足条件的直线，得到：

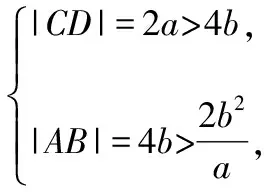
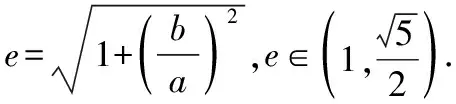
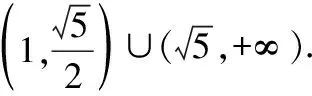
图2

这个题的解答如果没有图象，学生很难看明白为什么要分类，分类后又怎么去找关系列不等式.有了图象以后，就能通过有且仅有两条直线这个条件找到a，b，c之间的不等关系，求出离心率的范围.有图象后这样的直线有三条，四条一样也可以求出离心率的范围.

复习策略：直观想象是指借助几何直观和空间想象能力感知事物的形态与变化，利用图形理解和解决数学问题的素养.在直观想象素养的导向下，老师在高考一轮复习过程中，要突出圆锥曲线章节图形的重要性，让学生在做题的过程中养成先作图的习惯，然后再把题目的条件尽量放到图形中去，利用圆锥曲线图形描述和分析求解数学问题，进而建立形与数的联系，探索解决问题的思路.当然，准确作图的前提是要对圆锥曲线的知识有深度的了解，比如说圆锥曲线的对称性、双曲线的渐近线、抛物线的开口和准线等.

3 基于数据分析和数学运算核心素养，强化计算能力

前面提到解析几何具有代数的运算性质，因此在圆锥曲线题的解答过程中运算是必不可少的，而且有时候运算量很大.学生在做圆锥曲线解答题时，很多时候是有思路但输在了计算.

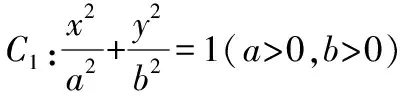
(1)求椭圆C1的方程；

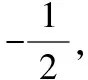
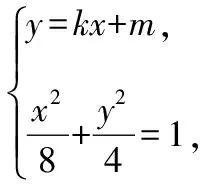
Δ=16k2m2-(8m2-32)(2k2+1)>0，得m2<8k2+4，

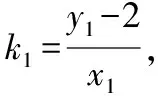
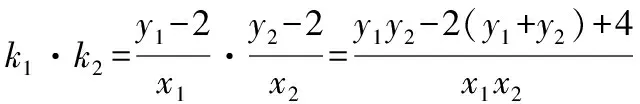
所以m=0，直线l的方程为y=kx，

因为|AN|=|BN|，所以ON垂直平分线段AB，

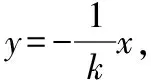
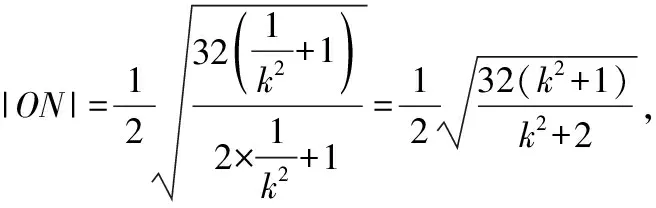
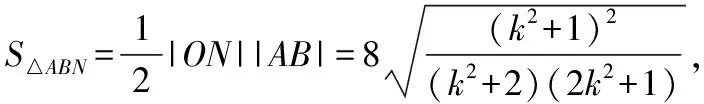
当k=0时，△ABN的面积也符合上式，

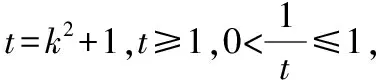
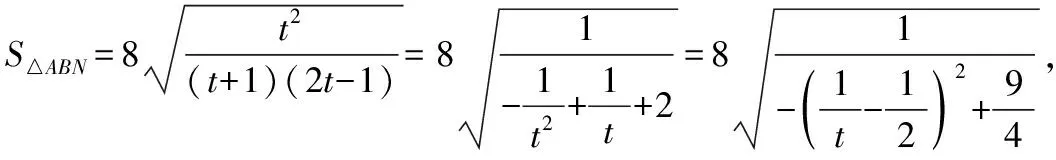
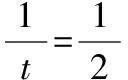
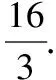
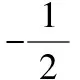
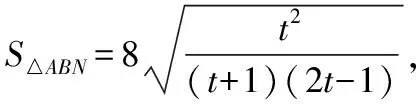
4 基于逻辑推理核心素养，强化结论的变式推广

由于椭圆、双曲线、抛物线具有很好的对称性，因此它们的很多结论都可以变式推广，很多结论也可以相互之间类比和拓展，通过变式推广和类比推理加强圆锥曲线知识的联系、开拓解题思路和培养创新思维.

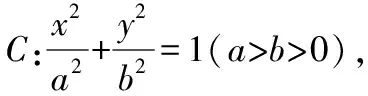
(Ⅰ)求C的方程；

(Ⅱ)设直线l不经过P2点且与C相交于A，B两点.若直线P2A与直线P2B的斜率的和为-1，证明：l过定点.

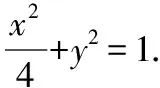
(Ⅱ)证明略.

在证明完l过定点(2，-1)后，考虑到2和-1与长半轴短半轴吻合的特殊性，可以对结论做出如下的变式推广：

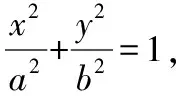
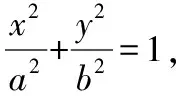
通过两个变式推广及其论证，加深了学生对圆锥曲线定点问题的论证思路.

复习策略：逻辑推理是指从一些事实和命题出发，依据规则推出其他命题的素养.逻辑推理素养导向下，高考一轮复习过程中，首先要加强培养学生逻辑推理的意识，主要有归纳、类比和演绎.然后再通过具体的知识内部以及知识与知识之间的关联，发现问题和提出问题.在复习圆锥曲线时，可以将特殊的结论一般化，主要是把条件的特殊性推广为一般性，探索结论是否仍然成立.由于椭圆、双曲线和抛物线都是平面截圆锥产生的曲线，其中一种曲线所具备的性质在另外的曲线中常可以推导出类似的结论，因此也可以将椭圆、双曲线和抛物线之间的结论通过适当改变条件，探索彼此之间结论的互通性，发现我们未知的圆锥曲线的性质.

以上基于数学核心素养导向，结合圆锥曲线章节的内容，从四个层面探究高考一轮复习的策略.这些策略同样也适用于其他的知识章节，如数列章节的复习，我们要加强等差等比之间的变式推广等.在函数章节复习中，加强数学抽象及数形结合思想方法.在概率统计章节中要加强数据获取及其数学运算能力，等等.总之，在整个数学一轮复习中，虽然是对高一高二学过的所有数学知识点进行全面的复习，但不能是简单的重复罗列，老师在一轮复习过程中要基于对章节知识整体把握的基础上，以数学核心素养为导向，通过一轮复习，深化学生对基础知识的理解，完善学生的知识结构，培养学生思维的广阔性，最终提升学生的成绩.