基本知识为载体、能力选拔为目的、学科素养为核心 ——2019年全国卷Ⅰ理科第21题折射出的高考命题规律

安徽

一、高考试题呈现

【试题呈现1】(2019·全国卷Ⅰ理·21)为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验.试验方案如下：每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠，随机选一只施以甲药，另一只施以乙药.一轮的治疗结果得出后，再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效.为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得-1分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得-1分；若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X.

(Ⅰ)求X的分布列；

(Ⅱ)若甲药、乙药在试验开始时都赋予4分，pi(i=0,1,…,8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0=0，p8=1，pi=api-1+bpi+cpi+1(i=1,2,…,7)，其中a=P(X=-1)，b=P(X=0)，c=P(X=1).假设α=0.5，β=0.8.

(ⅰ)证明：{pi+1-pi}(i=0,1,2,…,7)为等比数列；

(ⅱ)求p4，并根据p4的值解释这种试验方案的合理性.

【试题分析】本题是2019年全国卷Ⅰ最具代表性的题目之一.命题角度新，命题立意广，无论是知识立意，还是能力立意都体现了命题者的别具匠心.通过一道题把数学抽象、逻辑推理、数学建模、直观想象、数学运算以及数据分析六大核心素养融为一体.这种把能力立意提升到学科素养立意，目的就是以数学知识为载体，培养学生的数学思维和数学精神，同时也满足了高校对人才选拔的需求.

【解法剖析】(Ⅰ)要解决的问题就是概率统计的常规性问题——分布列的求法，通过对题意的分析不难得出随机变量X的可能取值为-1,0,1，不同的是，通常我们接触的概率值是具体的数值，而本题需要用字母来表示，在无形中增加了难度，对考生审题能力和处理数据能力的要求都提高了.(Ⅱ)第二问把概率问题与数列递推公式、等比数列以及方程思想和迭代思想结合在一起.

【解析】(Ⅰ)X的所有可能取值为-1,0,1.P(X=-1)=(1-α)β，P(X=0)=αβ+(1-α)(1-β)，P(X=1)=α(1-β)，所以X的分布列为

X-101P(1-α)βαβ+(1-α)(1-β)α(1-β)

(Ⅱ)(ⅰ)由(Ⅰ)得a=0.4,b=0.5,c=0.1.因此pi=0.4pi-1+0.5pi+0.1pi+1，故0.1(pi+1-pi)=0.4(pi-pi-1)，即pi+1-pi=4(pi-pi-1).又因为p1-p0=p1≠0，

所以{pi+1-pi}(i=0,1,2,…,7)为公比为4，首项为p1的等比数列.

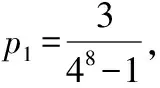
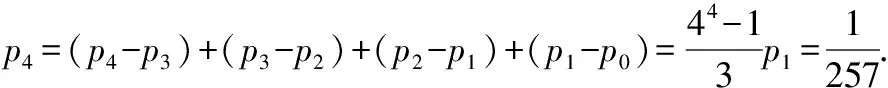
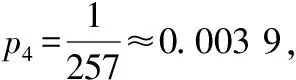
【解题反思】从解答过程可以知道，本题第一问的切入点并不高，只是一个基本的离散型随机变量的概率分布列问题，整个解题过程中的计算难度也并不复杂，本题的难度主要体现在审题困难、抽象困难、建模困难和数据处理困难上，这些困难恰恰是本题对数学核心素养的考查，也恰恰是高考对学生能力的考查.

二、命题规律探寻

纵观历年的高考数学试题，数学试题一直稳中求进，立足考纲、考查能力和选拔人才.把概率统计问题作为高考压轴题，是在继续保持以往高考数学试题的特点之外，让高考数学的应用性更强，实用性更强，试题的背景和来源更加贴近生活.这也是新时代对数学教学、数学核心素养和数学考试的新要求.高考的这种变化不是偶然，而是必然，也为广大一线教师指明，在今后的高考的压轴题会打破一成不变的命题方式，命题的立意和广度上都需要更加贴切数学应用和数学实用的思想，能够全面地考查数学核心素养，同时能够体现知识性、实用性、学科素养以及数学能力.

早在2014年江西省高考理科数学第21题就把概率统计、排列组合以及数学归纳法结合在一起来考查，那年这一题对考生的杀伤力也是很大的.

【试题呈现2】(2014·江西卷理·21)随机将1,2,…,2n(n∈N*,n≥2)这2n个连续正整数分成A,B两组，每组n个数，A组最小数为a1，最大数为a2；B组最小数为b1，最大数为b2，记ξ=a2-a1,η=b2-b1.

(Ⅰ)当n=3时，求ξ的分布列和数学期望；

(Ⅱ)令C表示事件“ξ与η的取值恰好相等”，求事件C发生的概率P(C)；

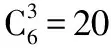
【解析】略.

【解题反思】本题的特点与2019年全国卷Ⅰ理科第21题的命题立意高度相似，试题从逻辑推理、数学抽象、数学建模和数据分析等方面全面考查学生的核心素养，尤其是第(3)问的处理，要冷静不怕麻烦，找到数据的生成过程，问题必然迎刃而解.

三、高考折射命题趋势

通过对高考试题的分析，我们不难得出，概率统计问题在高考中的地位举足轻重，尤其是在全面考查学生的核心素养以及能力方面更是起到空前的作用.这也必将是今后高考压轴题、各地区模拟考试和学生学业水平综合素质测试的命题方向.

2019年4月，笔者参与蚌埠市第三次质量检测命题，在试题讨论环节，命题组长陈耀忠老师就提出2019年全国卷Ⅰ理科数学压轴题应该是概率统计问题，但遗憾的是，由于第三次质量检测是高考前最近的一次大型模考，为了追求试题与往年高考题型的“稳定”，又能体现概率统计问题在高考中的地位越来越重要，我们把概率统计题从通常的18或19题的位置，大胆地移到了20题的位置，其目的就是要考生和老师知道概率统计问题在高考中的地位.

【试题呈现3】(蚌埠市2019届高三年级第三次教学质量检测)某地种植常规稻α和杂交稻β，常规稻α的亩产稳定为485公斤，今年单价为3.70元/公斤，估计明年单价不变的可能性为10%，变为3.90元/公斤的可能性为70%，变为4.00元/公斤的可能性为20%.统计杂交稻β的亩产数据，得到亩产的频率分布直方图如图①.统计近10年杂交稻β的单价(单位：元/公斤)与种植亩数(单位：万亩)的关系，得到的10组数据记为(xi,yi)(i=1,2,…,10)，并得到散点图如图②.

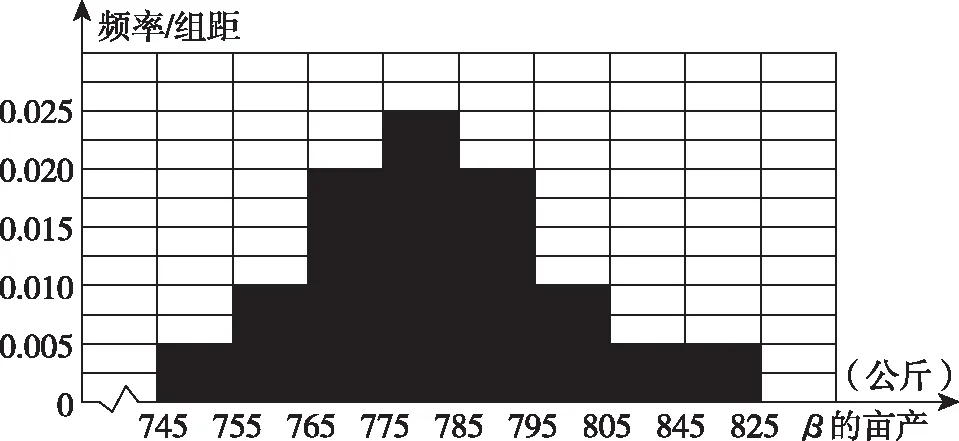
图①

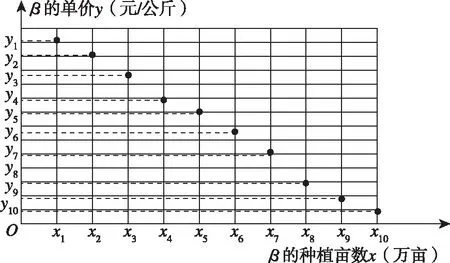
图②

(Ⅰ)根据以上数据估计明年常规稻α的单价平均值；

(Ⅱ)在频率分布直方图中，各组的取值按中间值来计算，求杂交稻β的亩产平均值；以频率作为概率，预计将来三年中至少有二年，杂交稻β的亩产超过795公斤的概率；

(Ⅲ)(ⅰ)判断杂交稻β的单价y(单位：元/公斤)与种植亩数x(单位：万亩)是否线性相关？若相关，试根据以下的参考数据求出y关于x的线性回归方程；

(ⅱ)调查得知明年此地杂交稻β的种植亩数预计为2万亩.若在常规稻α和杂交稻β中选择，明年种植哪种水稻收入更高？

【试题分析】本题从考查的知识性、能力性和核心素养方面都与高考压轴题较为接近，不同的是，本题侧重考查的是线性回归，并把决策性问题和不等式知识相结合，这是本题的亮点，唯一遗憾的就是本题未能与数列知识相交汇.

【解析】(Ⅰ)设明年常规稻α的单价为ξ，则ξ的分布列为

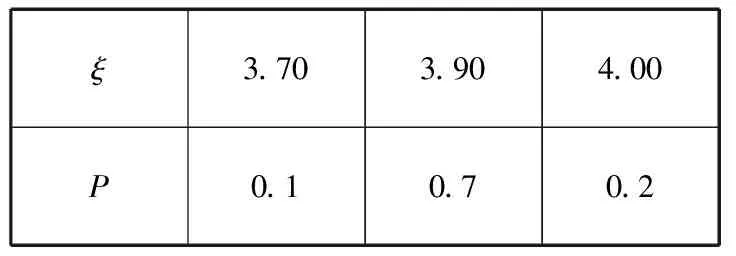
ξ3.703.904.00P0.10.70.2

E(ξ)=3.7×0.1+3.9×0.7+4×0.2=3.9，

估计明年常规稻α的单价平均值为3.9元/公斤.

(Ⅱ)杂交稻β的亩产平均值为：

[(750+810+820)×0.005+(760+800)×0.01+(770+790)×0.02+780×0.025]×10=78.2×10=782.

依题意知杂交稻β的亩产超过795公斤的概率为P=0.1+0.05×2=0.2，

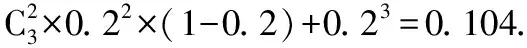
(Ⅲ)(ⅰ)因为散点图中各点大致分布在一条直线附近，

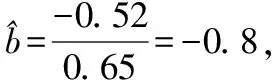
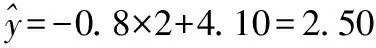
估计明年杂交稻β的每亩平均收入为782×2.50=1 955元/亩，

估计明年常规稻α的每亩平均收入为485×E(ξ)=485×3.9=1 891.5元/亩，

因为1 955>1 891.5，所以明年选择种植杂交稻β收入更高.

四、命题方向与时俱进

每年的高考试题都具有划时代的意义和风向标的作用，同时也是教学理念和时代发展紧密相连的体现.2019年高考全国卷Ⅰ理科用概率统计作为解答题的压轴题，这种导向同时也渗透即将实行的高考改革的理念和为新教材的投入使用奠定了一定的基础.在即将投入使用的北师大版新教材中关于统计部分在第六章第5节新增了分层随机抽样的均值和方差，这一块知识在以往的高中教材中没有涉及，但是这一知识已在地市级模考中出现.

【试题呈现4】(山西省2019年高三考前适应性测试)在一次高三年级统一考试中，数学试卷有一道满分10分的选做题，学生可以从A，B两道题目中任选一题作答.某校有900名高三学生参加了本次考试，为了了解该校学生解答该选做题的得分情况，计划从900名考生的选做题成绩中随机抽取一个容量为10的样本，为此将900名考生选做题的成绩按照随机顺序依次编号为001—900.

(Ⅰ)若采用随机数表法抽样，并按照以下随机数表，以方框内的数字5为起点，从左向右依次读取数据，每次读取三位随机数，一行读数用完之后接下一行左端.写出样本编号的中位数；

05 26 93 70 60 22 35 85 15 13 92 03 51 59 77

59 56 78 06 83 52 91 05 70 74 07 97 10 88 23

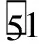
58 05 77 09 51 51 26 87 85 85 54 87 66 47 54

73 32 08 11 12 44 95 92 63 16 29 56 24 29 48

26 99 61 65 53 58 37 78 80 70 42 10 50 67 42

32 17 55 85 74 94 44 67 16 94 14 65 52 68 75

87 59 36 22 41 26 78 63 06 55 13 08 27 01 50

15 29 39 39 43

(Ⅱ)若采用系统抽样法抽样，且样本中最小编号为008，求样本中所有编号之和；

(Ⅲ)若采用分层抽样，按照学生选择A题目或B题目，将成绩分为两层，且样本中A题目的成绩有8个，平均数为7，方差为4；样本中B题目的成绩有2个，平均数为8，方差为1.用样本估计900名考生选做题得分的平均数与方差.

【试题分析】本题前两问都是常考问题，然而第(Ⅲ)问的这种分层随机抽样的均值和方差的求解让考生摸不着头脑，这类问题依然是以均值和方差的求法作为载体，只是考查的角度不同.(Ⅰ)由题取出十个编号，先将编号从小到大排列再求中位数；(Ⅱ)按照系统抽样法抽出的编号可组成以8为首项，以90为公差的等差数列，求该数列的前10项和；(Ⅲ)分别求出样本的平均数和方差，900名考生选做题得分的平均数与方差和样本的平均数与方差相等.

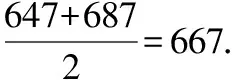
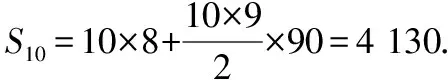
(Ⅲ)记样本中8个A题目成绩分别为x1，x2，…，x8，2个B题目成绩分别为y1，y2，

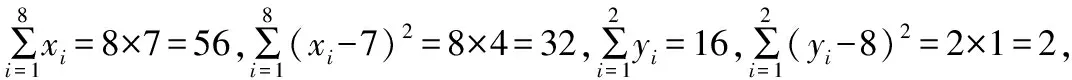
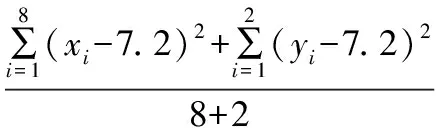
故估计该校900名考生该选做题得分的平均数为7.2，方差为3.56.

大数据推动着社会高速发展，这也体现了统计学的研究价值越来越大，概率统计问题无疑是最贴近生活和社会发展的.高考的命题以基本知识为载体、以能力选拔为目的、以考查学科素养为核心，同时高考的命题也必将与时俱进，概率与统计知识以及一切贴近生活的数学知识都必将成为高考命题的重要素材，也是高考命题的风向标.