基于DCCA-NSEn的系统耦合网络建模与评估*

冯龙飞， 高建民， 高智勇， 谢军太， 高 旭

(西安交通大学机械制造系统工程国家重点实验室 西安，710049)

引 言

流程工业生产系统生产设备繁多，且系统内部关联耦合度高，是一个分布式的复杂机电系统[1-3]。设备故障和工艺调整常常导致系统性的波动，及时准确地发现工业过程中的运行故障、合理评估故障过程的异常程度，对生产系统上下游进行合理调控非常重要[4-5]。利用有效的状态评估方法对系统运行状态做出及时准确的评估，为调度人员提供可靠的系统实时状态，是保障系统安全稳定运行的重要手段。

在复杂机电系统综合状态评估方面，李黎等[6]根据信息关联规则和因素空间理论的变权综合概念，提出了一种对电力变压器进行状态评估的方法。程瑛颖等[7]针对电能计量装置提出了一种基于数据的状态评估方法。姚云峰等[8]建立了基于改进证据理论的装备健康状态评估模型。但该类研究多关注系统的关键设备和部件，难以从整体上对系统的服役状态进行评估。

基于数据的时间序列分析方法，如DCCA、CDFA等方法[9]已广泛用于交通[10]、金融及股市[11]等领域，该类方法通过充分挖掘和分析时间序列数据中的信息，有效帮助了管理者的管理和决策。将这些方法应用于工业过程变量间的耦合关系分析，可及时获取过程监测变量间的耦合状态的变化，进而构建能够表征系统服役状态的耦合网络模型。这对系统上下游的快速精准调度，和系统的精细化管控具有辅助作用，有助于提升流程工业生产过程的安全运行水平。

谭跃进等[12]提出了网络结构熵的概念，阐述了网络结构熵与连接度分布的关系，对网络的异构特性进行了定量描述。而复杂机电系统生产过程具有较强的耦合性，各变量之间相互影响从而形成了基于耦合关系的网络模型。系统异常从网络结构熵的角度来看，就是系统的异构性发生变化的过程。因此，笔者通过网络结构熵理论，对系统耦合网络模型的异构性进行定量分析来实现系统的状态评估。

1 基础理论

1.1 时间序列耦合性分析的DCCA方法

2008年，Podobnik等[13]提出消除趋势相关分析方法，成为首个描述两列非平稳时间序列幂律相关关系的技术手段。DCCA方法基于随机游走理论，通过计算去趋势协方差最小化外部趋势对相关性探测的影响。

流程工业的生产过程具有强耦合性，其监测变量之间也存在着不同程度的耦合关系，笔者在此将DCCA算法应用于变量耦合关系分析。算法流程[14-15]如下。

(1)

4) 定义两序列间的去趋势游走，其值是每个盒子内集成序列与局部趋势之间的差值，即

(2)

5) 计算每个盒子内的协方差，即

(3)

(4)

FDCCA(n)～nh

(5)

其中：h为DCCA标度指数。

DCCA标度指数表征两序列间耦合特征，即衡量两序列间的耦合强度。

1.2 网络结构熵

复杂网络理论中包含众多统计参数，如节点度、累计度分布及网络结构熵等。笔者从网络结构熵的角度对系统耦合网络的状态演变过程进行分析，通过系统网络模型的异构性变化来表征系统的服役状态,流程如下。

1) 网络模型的点强度计算[16-17]

(6)

其中：Ni为与节点i相连接的近邻点的个数；Wij为节点i到j的权重。

2) 网络点强度分布计算

(7)

其中：n为强度ki的节点总数；N为节点总数。

3) 现实中复杂网络有少量具有高连通度的中枢节点和大量具有低连通度的节点，即无标度性。熵是系统的一种无序的度量，基于度分布的网络结构熵可以度量复杂网络的序状态。其定义[18]为

(8)

4) 为消除节点数目N对E的影响，采用标准结构熵[20]

(9)

2 基于DCCA-NSEn的多变量状态评估

流程工业过程监测变量之间具有复杂的耦合性，耦合关系的变化过程蕴含了系统状态的演变信息。因此，基于变量之间的耦合关系可以构建能够反映系统服役状态的耦合网络模型。笔者利用DCCA算法对变量耦合关系进行分析，并结合网络结构熵方法分析耦合网络模型的状态演变过程，提出了一种基于DCCA和NSEn的系统综合状态评估方法。

DCCA-NSEn方法对监测变量进行分析的最终目的是根据实时生产数据，实现流程工业生产系统的准确合理的评估。当系统状态发生异常时能够及时的报警提示相关责任人员，避免故障进行恶性传播，形成系统级故障而造成难以挽回的后果。DCCA-NSEn方法与历史正常监测数据和实时监测数据相结合，进行系统状态评估和异常报警的具体流程如图1所示。本方法适合于对长序列进行迭代分析，对长周期缓变的故障有很好的评估效果。

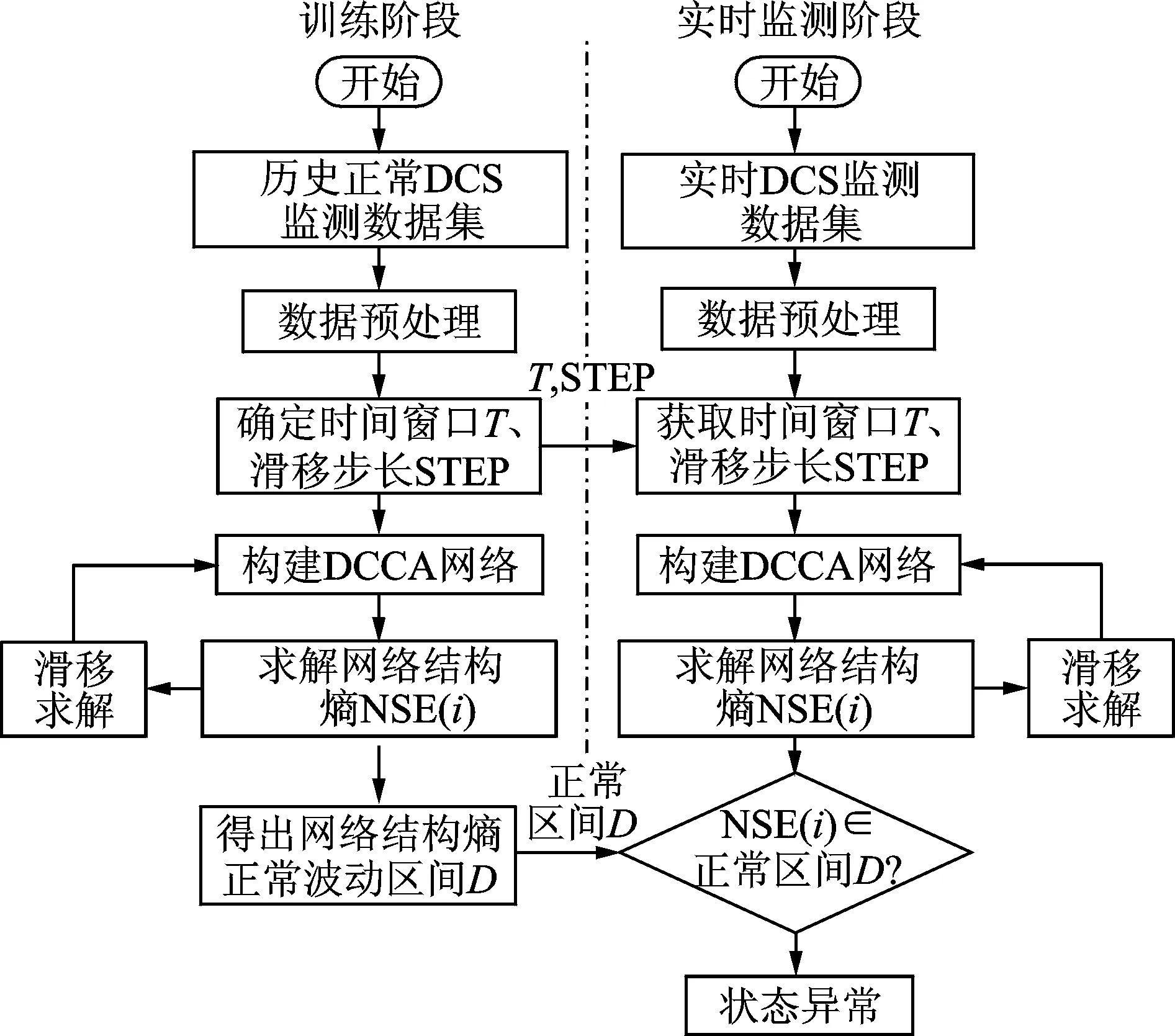
图1 DCCA-NSEn方法状态评估流程图Fig.1 DCCA-NSEn method state assessment flow chart

2.1 监测数据集预处理

流程工业系统监测数据具有异源异构的特点，且工况恶劣导致监测数据中存在噪声干扰，直接进行分析的话很难反映变量间的真实耦合关系。所以，进行数据处理之前首先要进行数据预处理。

归一化处理：对于变量X内的每一个值，进行如式(10)处理

X(i)=X(i)/mean(X)

(10)

降噪处理：为降低噪声干扰对状态评估过程的干扰作用，此处采用的是小波包降噪算法进行降噪处理。

2.2 时间窗口宽度的选取

时间序列真实地记录了动态系统的历史信息，因而包含了系统结构特征和运行规律。DCCA算法能够从采集得到的时间序列中，取其中有限长的一段时间序列，对两变量之间的耦合度进行分析。因此所选序列长度T必须能够反映变量的特征。

在此，笔者采用FFT算法对监测变量的拟周期进行计算，得到n个时间序列的拟周期。为使得序列长度能尽最大可能反映每一个变量的特征，此处以变量中最大拟周期为参考，选取最大周期的2倍作为序列的时间窗宽度，即T=2Tmax。

2.3 DCCA指数网络的构建

对于n个时间序列x1，x2，x3，…，xn，分别计算其两两之间的DCCA指数，DCCA(x1，x1)，DCCA(x1，x2)，…，DCCA(xn，xn)，形成一个n×n的DCCA矩阵D。

(11)

如式(11)所示，x1～xn为所选的n个要评估的变量。其中，dij为变量xi与变量xj的DCCA指数，即代表了两变量之间的耦合度。由n个变量两两之间的耦合度，构成了这样一个N节点的耦合度网络。由于DCCA方法是无向的，使得dij=dji，所以D矩阵是一个对称矩阵。D包含了n个变量中任何两个变量的相关性关系，对其特征分析能够同时监测到每一个变量与其他所有变量之间的耦合度变化。

2.4 基于NSEn的系统服役综合状态表征

当系统发生异常状态时，变量之间的耦合关系也会发生不同程度的变化，从而驱动了耦合网络特征的演变。本方法认为，当耦合网络的网络结构熵发生较大变化时，系统的服役状态发生异常。

如2.3节所述，对监测时间序列进行滑移求解可得到连续的耦合度网络。其网络结构熵曲线的连续变化过程可以反映系统的服役状态。当系统处于正常运行状态时，网络结构熵稳定在一定的区间内波动；当系统出现故障时，各变量相关性出现异常，耦合网络的网络结构熵会出现大幅度的变化，并超出合理阈值。

3 实例验证

3.1 监测时间序列变量选择

压缩机组作为流程工业系统的典型单元，其安全运行对于整个流程工业生产过程稳定运行至关重要。文中应用某煤化工企业的在一次部分设备故障停车前13天去除压缩机组的故障监测数据进行分析，其故障可描述为：在5月上旬，先后出现了多次异常工况，第1次出现异常，由于系统自身存在调节机制，恢复到了正常状态，很快又出现了更严重的异常，经过紧急维修，在一定程度上恢复了系统性能，但系统还是处于持续的异常状态，如此反复导致大部分设备在5月13号被迫故障停车，进行检修。在此过程中，选用与故障相关的5个监测变量如表1所示。以故障发展初期到严重阶段的数据为基础进行分析，验证本方法对系统状态评估的有效性。

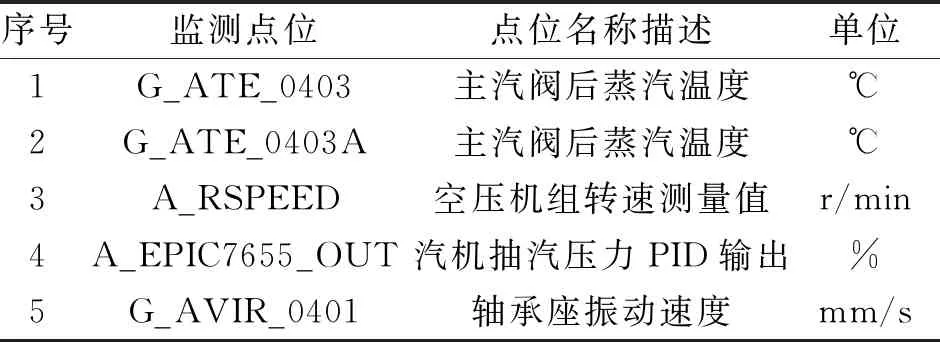
表1 压缩机组监控变量表

3.2 数据预处理

进行数据分析之前，需先将原始监测数据转化为可统一分析的时间序列，此处分为两步进行处理，即数据归一化处理和数据降噪处理。

此处采用了小波包降噪的方法。数据降噪过程分为分解和重构两个步骤：a.对不同变量采取合适的小波基函数和分解层数，用固定阈值方法对分解后的各小波细节系数进行软阈值处理；b.重构最后一层近似系数和所有层的细节系数，得到降噪后的变量时序图，如图2所示，其中横坐标为时间t，纵坐标为归一化的振动量T′。

由图2可知，归一化的数据降噪之后，信号的总体趋势不发生变化，且滤掉了部分高频噪声。

图2 变量G_AVIR_0401降噪前后效果图Fig.2 Comparison of variable G_AVIR_0401 before and after the noise reduction

3.3 求时间序列滑移窗口宽度W

为使数据尽最大可能反映数据的特征，提高DCCA算法计算变量间耦合度的准确性，此处采用FFT算法进行每一段序列的拟周期T进行计算，监测点每分钟采样一次。取最大拟周期Tmax的2倍周期作为滑移时间窗口W，即W=2max(T(1),T(2),…,T(n))。笔者选用了5个变量进行综合分析，每个变量的拟周期求解结果如表2所示。窗口宽度为2 500，即时间窗宽度为2 500 min。

表2 各变量的拟周期计算

3.4 监测变量间的耦合性分析及构建

为分析在随时间变化的过程中哪些变量之间的耦合度发生了变化，绘制DCCA指数变化曲线如图3所示。

图3 两两变量之间DCCA指数变化图Fig.3 DCCA coefficient variation between two variables

图3中，横坐标为滑动窗口号，纵坐标为DCCA指数值。由图可知：各变量间的DCCA指数变化趋势有的能够部分反映系统的状态异常信息，有的基本没有发生太大变化。可见，如果仅使用某两个变量的耦合度来反映系统的状态，则会带来系统评估过于片面，从而得出不准确、甚至错误的结论。在此，用DCCA算法计算变量之间的相关性，并构建监测变量耦合度网络。按2.3中的方法进行构建，式(12)为第1段窗口的耦合度网络。

D1=

(12)

在耦合度分析过程中，可用DCCA指数来判定两变量的耦合度。一般认为DCCA指数小于0.3时，变量间具有微弱耦合关系，当其处于0.3～0.7之间时为具有中等强度耦合关系，若其大于0.7，则具有强耦合关系。

在此处，为使得分析结果趋于稳定，辨识度高，去除弱相关元素，去除规则如式(13)所示。

D(i,j)=

(13)

3.5 基于NSEn的系统服役状态演化规律分析

计算得其网络结构熵的变化如图4所示。选取点1代表系统正常状态、点2，3代表系统的异常状态，分析在此窗口时各变量之间的相关性，如图5所示。

图4 网络结构熵随时间变化曲线Fig.4 The entropy of network structure changes with time

图5 系统不同状态下变量耦合网络Fig.5 Variable coupling network of systems in different states

由图5知，在7天过程中，系统刚开始处于正常状态，与之相对应的，其NSEn值非常平稳地稳定在0.75～0.80之间。到第4天发生异常时，网络结构熵值发生了很大的变化，NSEn逐渐变为了0.4。后由于系统存在的自动修复性能，状态恢复了正常，网络结构熵值也回升到正常区间。之后再次发生更严重的故障，NSEn值发生了非常剧烈的波动，后经过维修，系统性能恢复到了一定的水平，NSEn值也有所恢复，但未达到正常区间之内，系统仍处于持续异常状态。

为进一步分析在各阶段时，变量之间的相关性变化，图5进行多变量相关性分析[19]。蓝色线代表部分相关，粗红线代表强相关，虚线代表弱相关或不相关。

图4中1点为系统处于正常运行状态，此时各变量之间的耦合关系网络如图5(a)所示，当系统处于正常状态时，系统耦合关系网络基本不发生变化。2点为系统处于异常运行状态，此时各变量之间的耦合关系网络如图5(b)所示，与图5(a)相比发现网络模型发生了较大的变化，此时系统出现了一定的异常，但系统自动恢复了正常状态。随后系统发生了更加剧烈的异常状态，取3点为代表，当系统状态剧烈恶化时，其变量间的耦合关系网络如图5(c)所示，变量间的相关性发生了剧烈的变化。通过图(a)～(c)的对比可发现，当系统处于正常状态时，各变量之间的耦合关系网络比较稳定；当系统发生不同程度的异常状态时，变量间的耦合关系网络也会发生不同程度的变化。

通过图4,5的分析得出，笔者所提出的DCCA-NSEn方法不仅能判断系统是否发生了异常，还能对系统运行状态的异常程度进行评估。

3.6 其他多变量综合状态评估方法

CDFA是广义多变量去趋势协方差函数分析针对非线性、非平稳性的多个状态信息序列间耦合特性的方法[20]。在CDFA算法流程中，可以从绘制的多重分形谱曲线中提取分形特征。此处采取广义赫斯特指数h(q)、谱高度Δf(Δf=f(α)max-f(α)min)以及Holder指数的最大值和最小值4个特征作为特征组合(h(q)，Δf，αmax，αmin)。通过这些耦合关系特征的变化对系统运行状态进行评估。

为了将CDFA方法与笔者提出的DCCA-NSEn方法进行对比，此处采用上述数据进行CDFA方法的分析评估，CDFA方法所得评估结果如图6所示。图6中横坐标为滑动窗口号，纵坐标为各项特征参数。

经过CDFA方法分析，得到(h(q)，Δf，αmax，αmin)4个组合特征的变化曲线。由图6观察得，在系统初期运行时，4个特征指数都相对平稳，滑动超过30步以后，各指数都有上升趋势。这说明对系统的异常状态有一定的检测效果。

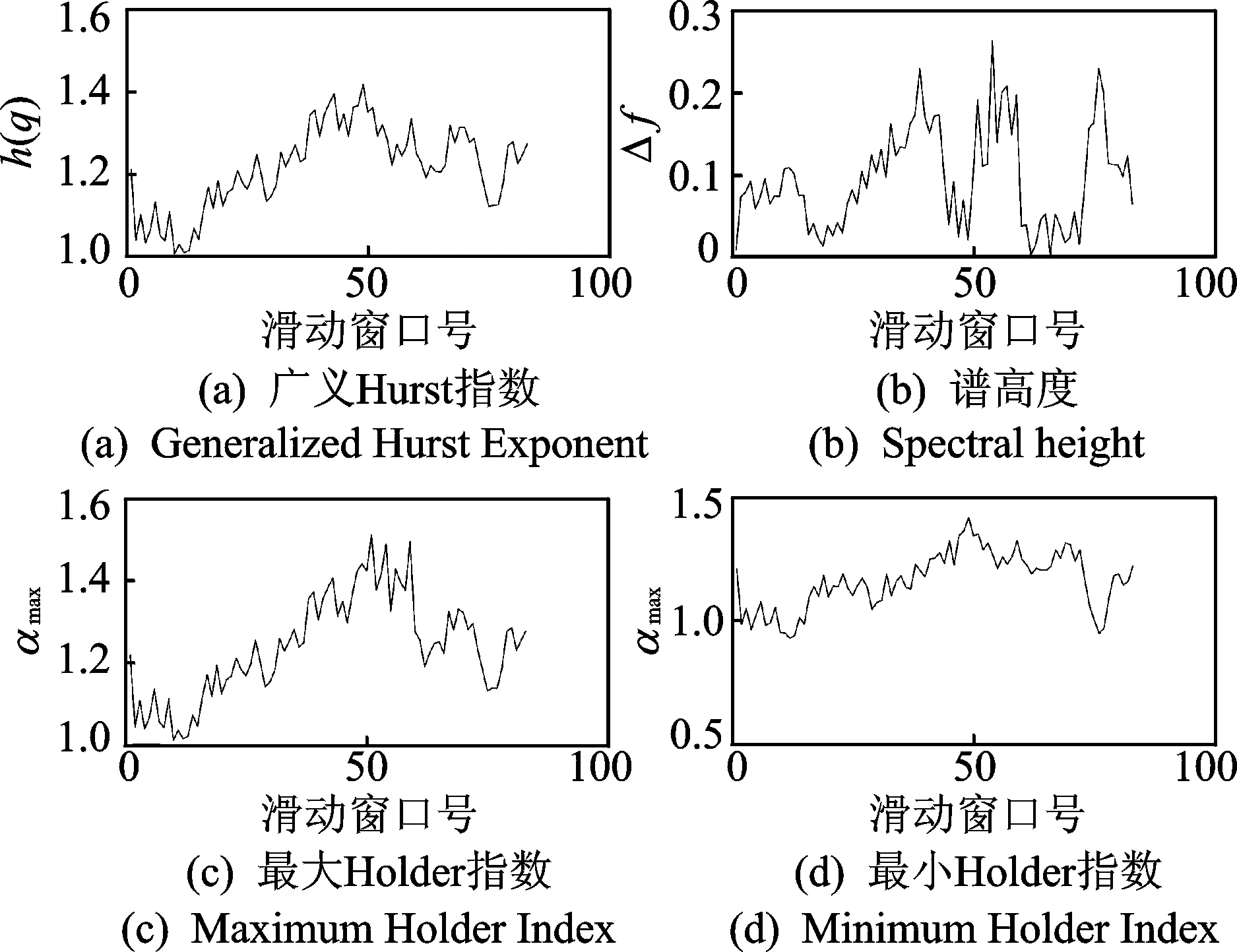
图6 CDFA方法提取耦合特征Fig.6 CDFA method extracts the coupling characteristics

3.7 方法评价与对比

流程工业生产系统中一般是通过各种控制系统使得其状态变量随时间在某一范围内变化，因此具有连续流程的化工生产都是在定态下进行的。DCCA方法是对两变量耦合度的评价，所以当系统正常运行时，其耦合度保持在一定范围内波动；当发生异常时耦合度会有较大的波动。由图4,5可知，当监测变量众多，对两两变量之间的耦合性分析不能反映出系统生产运行的综合状态，故此处引入了网络结构熵的方法对原方法进行改进，得到很好的综合评估效果。

笔者提出的DCCA-NSEn方法与CDFA方法进行对比，有以下优点：a.DCCA-NSEn方法的所得的特征曲线较CDFA方法，当系统正常运行时，曲线走势更加平稳；当系统出现异常时，则波动更加剧烈、明显。b.由3.5节中结果分析可知，DCCA-NSEn方法较CDFA方法不仅能够判别系统是否异常，对系统发生异常的程度也有一定的评估效果。c.DCCA-NSEn方法用变量间DCCA系数网络的网络结构熵的变化来评估系统运行状态，较CDFA方法不仅能评估系统运行状态，同时能够把控系统网络模型的动态演化。

4 结束语

笔者提出了一种基于去趋势交叉分析方法和网络结构熵理论的流程工业系统多变量综合评估的方法，并提出一种利用DCCA系数构建复杂机电系统的网络模型。根据FFT方法计算序列拟周期，以此确定时间窗口宽度，利用去趋势交叉分析方法对监测变量两两之间的耦合性进行分析。经过处理后，去除弱相关因素的影响，构建了反映系统服役状态演化特征的耦合网络模型,时间窗口在时间轴上滑移。提出了一种运用网络结构熵研究系统耦合网络模型的演化特征。利用网络结构熵在网络结构异构性表征的优势，定量表达变量间相关性变化规律，为故障预警和过程恢复评估提供决策支持。

应用某化工企业压缩机组的实际生产数据对该方法进行验证，并且将验证结果与多变量评估的CDFA方法进行对比分析。结果表明:本方法评估在系统正常状态下网络结构熵变化较为稳定，异常状态下曲线变化敏感，所以对流程工业的状态评估具有较好的评估效果。当系统发生不同程度的异常时，网络的连接方式也会发生不同程度的变化，这些变化都体现在了网络结构熵的变化中。这也验证了DCCA-NSEn方法的合理性。