超声纵-扭复合钻削系统的力负载影响研究*

常宝琪， 赵 波， 原路生， 李鹏涛， 赵重阳

(河南理工大学机械与动力工程学院 焦作，454000)

引 言

钛合金(Ti6A14V)作为一种先进材料，具有强度大、抗蚀性好、耐磨损、耐热性强及密度小等性能，被广泛应用于现代航空航天工业[1-2]。同时，钛合金属于难加工材料，传统钻削加工难以实现高质高效的加工效果。超声辅助钻削加工作为一种先进的特种加工技术，在钛合金和镍合金等难加工金属材料的钻孔过程获得良好的工艺效果，有效降低了孔表面粗糙度、孔出口毛刺高度和刀具磨损[3-5]。但是在超声辅助钻削钛合金等难加工材料中，较大力负载的出现会使声学系统的电流波动、频率偏移，导致声学系统不稳定甚至失谐。因此，研究力负载变化对声学系统特性的影响机理和规律，对提高超声辅助钻削加工效果具有十分重要的意义。

关于负载对超声振动系统特性的影响，已有学者进行了相关研究。伊晓春等[6]基于瞬态波传播理论，研究了周期激励下阶梯形变幅杆重复撞击加工工件的瞬态动力响应及特性变化。文献[7]根据刀具的几何参数变化，分析刀具负载对超声铣削声学系统稳定性的影响。针对力负载，刘折等[8]通过研究负载施加接触方式为点、线、面时，负载对超声加工声学系统特性的影响。文献[9]研究了超声车削中车削力与切削速度﹑切削深度以及切削质量之间的关系。张云电等[10]通过分析不同珩磨方式下的珩磨压力，得出系统承受不同珩磨力下谐振频率的变化规律。纪华伟等[11]通过对超声切割声学系统理论模型的建立，得到超声切割力与系统谐振频率及阻抗之间的关系。也有学者利用有限元仿真和理论分析相结合的方式，揭示了刀具负载、换能器和变幅杆组成的振动系统的各种谐振状态特性,研究了系统的谐振设计方法[12]。

综上所述，对于钛合金材料超声钻削声学系统的研究略显不足，不同力负载下，超声钻削系统的阻抗值、振幅和谐振频率变化规律尚不明确，超声钻削系统在实际加工中不够稳定。根据以上问题以及实际加工中出现的系统失谐、振幅衰减甚至停振等现象，基于四端网络法对由换能器﹑复合变幅杆和负载三者组成的超声钻削声学系统进行理论分析，获得系统阻抗和放大系数随负载的变化规律。基于有限元仿真研究了模拟力和周期钻削力对声学系统振动特性的影响，通过模拟试验与钻削加工试验,研究了负载变化对超声振动参数的影响规律。

1 超声钻削声学系统整体理论模型

1.1 超声复合变幅杆的等效四端网络模型

笔者采用圆锥过渡型复合变幅杆，将复合变幅杆的每一段等效为一个机械四端网络,然后将各传输矩阵连续相乘,得到一个整体四端网络及其传输矩阵[13]。图1为圆锥过渡复合变幅杆的结构简图。图2为复合变幅杆的总体四端网络图。

图1 圆锥过渡复合变幅杆结构简图Fig.1 Conical transition composite horn structure diagram

图2 复合变幅杆总体四端网络图Fig.2 Composite horn overall four-terminal network diagram

根据一维纵振杆波动方程、力和位移的边界条件，得到各段变幅杆的传输方程[14]如下所示。

变幅杆大圆柱段传输方程

(1)

变幅杆圆锥段传输方程

(2)

变幅杆小圆柱段传输方程

(3)

其中：T1，T2，T3分别为变幅杆各段传输方程中的传输矩阵；S1和S2分别为复合变幅杆大端和小端面积；c1为声波在变幅杆中传播速度；k1=ω/c1为圆波数；ρ1为复合变幅杆的密度。

联立式(1)～(3)，可得复合变幅杆的总体传输方程为

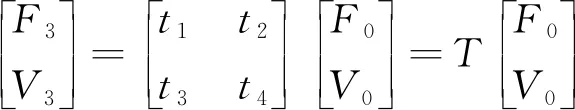
(4)

其中：T=T3T2T1。

1.2 压电陶瓷的等效四端网络模型

压电陶瓷是一个电输入到力输出的元件，压电陶瓷向两端面输出力，这两个端面分别与前﹑后端盖相连[15]。由于后端盖是作为声能的反射面，所有的负载以及工作端都在前端盖方向，故在分析时只选择前端盖作为研究对象。

图3 压电陶瓷四端网络示意图Fig.3 Piezoelectric ceramic four-terminal network schematic

根据使用条件和特性，笔者选择圆柱形压电陶瓷。当压电陶瓷满足一维轴向纵振时，对于无损耗的压电材料，结合牛顿第二定律、电荷守恒方程和边界条件，求得压电陶瓷传输方程[16]为

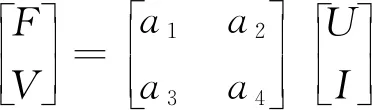
(5)

1.3 前端盖的等效四端网络模型

前端盖可以看作是一小段不具备放大作用的变幅杆，故前端盖的四端网络模型相似于等截面变幅杆四端网络模型。前端盖的传输方程为

(6)

1.4 带负载声学系统整体理论模型建立

利用四端网络法将超声声学系统的各部分结合在一起，使用ZF代表负载的统一参量。

根据图4可得声学系统的四端网络传输矩阵模型为

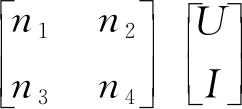
(7)

图4 带负载声学系统四端网络Fig.4 Four-terminal network with load acoustic system

为了方便计算及后面的分析，将传输矩阵中复数变量提取出来，令

(8)

变幅杆输入阻抗为变幅杆的输入端力与输入端振速之比。参考变幅杆输入阻抗的定义，声学系统的输入阻抗为

(9)

变幅杆的放大系数等于两端面的位移或者速度之比。参考变幅杆放大系数的定义，超声钻削声学系统整体放大系数的关系式为

(10)

由声学系统理论可知刀尖的瞬时位移为

S=Asin(2πft+b)

(11)

刀尖瞬时速度为

V0=S′=2πfAcos(2πft+b)

(12)

刀尖速度与振幅的关系可简化为

V=2πfA

(13)

将式(13)带入式(10)，得到负载、输出振幅和输入电流的关系式为

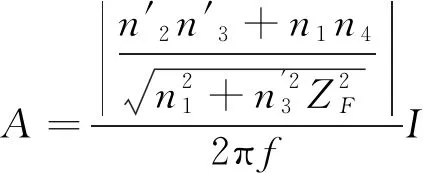
(14)

1.5 带负载声学系统数值计算及分析

确定系统的设计频率为35 kHz,复合变幅杆的几何参数[17]以及声学系统中各部分的性能参数如表1所示。四端网络参数如表2所示。

表1 声学系统性能参数表

表2 声学系统四端网络参数表

Tab.2 Acoustic system four-terminal network parameter table

类别参数大圆柱段C11=0.174C12=-3.41×10-5jC13=-2.84×104jC14=0.174圆锥段C21=-0.357C22=-6.8×10-5jC23=16 951.8j-1C24=0.44小圆柱段C31=0.724C32=-9.5×10-5jC33=-4 975.9jC34=0.724复合变幅杆t1=-2.927t2=4.82×10-5jt3=-1 221.28jt4=-0.362压电陶瓷a1=-21 764a2=-0.233ja3=-9.42×106ja4=1.819前端盖b1=0.395b2=-9.44×10-5jb3=-8 940.04jb4=0.395声学系统n1=1.86×108n2=0.169 5jn3=-5.76×105jn4=641.19

根据上述计算，将得到的声学系统四端网络参数带入式(9)，可得输入阻抗公式为

(15)

将声学系统四端网络参数带入式(14)，可得负载、输出振幅和输入电流的关系式为

(16)

当声学系统的调谐匹配无法进行快速响应时，系统存在静态匹配，输入阻抗的虚部无法被及时抵消。取输入阻抗虚部

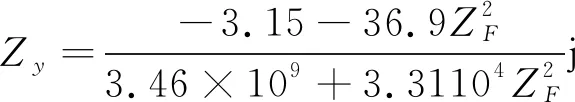
(17)

根据式(17)，用Matlab软件作图得到负载阻抗与输入阻抗虚部关系如图5所示。

声学系统作为超声波发生器的能量接受部分，其输入阻抗随负载阻抗的变化越小，接受能量就越稳定，系统的阻抗匹配与调谐匹配也就越容易完成。由图5可知，随着负载阻抗的增大，输入阻抗虚部先快速增加后趋于平稳。输入阻抗的快速变化导致使声学系统的阻抗匹配与调谐匹配无法迅速完成，从而导致谐振频率在系统匹配的过程中产生偏移。

图5 负载阻抗与输入阻抗虚部关系图Fig.5 Load impedance and input impedance imaginary relationship diagram

当声学系统的调谐匹配可以随时保持谐振时，系统存在动态匹配，则输入阻抗的虚部一直为零，此时取输入阻抗的实部

(18)

图6 负载阻抗与输入阻抗实部关系图Fig.6 Load impedance and input impedance real part relationship diagram

图7 负载阻抗-输入电流-输出振幅关系图Fig.7 Load impedance-input current-output amplitude relationship diagram

由式(18)利用Matlab软件作图得到负载阻抗与输入阻抗实部关系如图6所示。由图6可知，随着负载阻抗的增大，输入阻抗的实部先迅速增大，随后小幅减小。输入阻抗的增加会使系统的损耗升高，能量传输效率降低，影响系统阻抗匹配的过程，从而影响系统整体的稳定性。

根据式(16)得到负载阻抗、输入电流以及输出振幅之间的关系如图7所示。由图可知，随着负载阻抗值的增大，声学系统的输出振幅减小，输入电流增大，两者的比值逐渐减小。这说明负载阻抗越大，声学系统的放大系数就越小。

2 带负载超声纵-扭复合变幅杆有限元仿真

2.1 超声纵-扭复合变幅杆模态分析

通过理论设计35 kHz圆锥过渡型复合变幅杆，在复合变幅杆圆锥段开设3条均布螺旋沟槽，槽宽为6 mm,槽深为4 mm，螺旋角度为60°。使单向模态的纵向振动激励实现超声纵-扭复合振动输出。

根据理论推导的数据进行三维建模，在复合变幅杆节点处添加6 mm厚法兰盘，并在圆锥段开设3条均布螺旋沟槽。将模型导入分析软件Ansys中，对其进行模态分析。材料定义45钢，选用Workbench默认网格划分单元，模态拓展阶数为25，模态分析结果如图8所示。由图可知，纵-扭复合模态下的谐振频率为34 570 Hz，与理论值偏差430 Hz。分析其原因：a.开设沟槽后，变幅杆的质量发生变化，从而影响其谐振频率；b.螺旋沟槽结构使纵向振动转换为纵-扭复合振动，而纵向振动与扭转振动的波长不一样，其谐振频率也不相同；c.由于开设沟槽后，沟槽部分的刚性及强度减弱，施加相同的应力作用，沟槽部分的的变形量较大，即该部分材料的弹性模量E变小，而弹性模量E与波速c的平方成正比，波速c的减小会导致变幅杆谐振频率f的变化[18]。

图8 纵-扭复合变幅杆模态分析Fig.8 Modal analysis of longitudinal-torsional composite horn

2.2 超声纵-扭复合变幅杆谐响应分析

Ansys Workbench的谐响应分析可以在模态分析的基础上进行。设置分析的频率范围为0～34 570 Hz，分析数量为50个，在复合变幅杆的法兰处施加固定约束；查阅资料可知，换能器部分可提供3 μm的振动位移，因此在换能器前端盖与变幅杆接触面设置正弦式变化位移3 μm。分析结果如图9所示。由图可知，超声纵-扭复合变幅杆最大振幅处为变幅杆的小端面处，振幅大小为9.8 μm，相较于输入时3 μm，放大3.27倍。这说明变幅杆的设计及螺旋沟槽的开设较为合理。

图9 纵-扭复合变幅杆谐响应分析Fig.9 Harmonic response analysis of longitudinal-torsional composite horn

2.3 带刀具超声纵-扭复合变幅杆模态分析

在超声纵-扭复合变幅杆小端处添加ER系列弹性夹头、压帽及直径6 mm钻头，为了简化分析，三维建模时将钻头简化为直径6 mm圆棒，模态分析结果如图10所示。模态分析结果为34 306 Hz，相较开槽后下降264 Hz。分析其原因：a.弹性夹头、压帽及钻头通过装配组合在一起，影响声波的传输速率，波长不变声速和频率成正比关系，从而导致频率有所下降；b.弹性夹头、压帽及钻头的增加使变幅杆整体长度增加，声速不变的情况下，变幅杆半波长谐振长度增加，导致波长增加谐振频率降低。

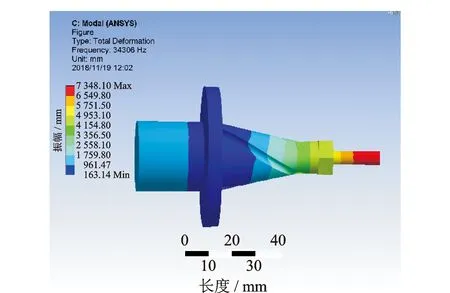
图10 带钻头纵-扭复合变幅杆模态分析Fig.10 Modal analysis of longitudinal-torsional composite horn with drill bit

2.4 超声纵-扭复合变幅杆预应力模态分析

预应力模态分析是在模态分析之前增加静力学分析，将静力学分析的结果带入模态分析里面。预应力模态分析是为了找出声学系统受力之后的模态规律。

根据实际加工时钻削力的大小，在钻头顶端施加0～500 N的轴向压力，设置求解阶数为25阶，得到谐振频率变化情况如图11所示。由图可知，带刀具超声纵-扭复合变幅杆在受到力负载后，其谐振频率整体呈上升趋势，但变化范围并不大。分析原因是预应力模态分析是在模态分析的基础上针对物体本身的结构模型进行分析的，只有当物体结构本身出现形变时，谐振频率才会出现较大的变化。超声纵-扭复合变幅杆在实际工作时，钻削力对其本身结构并不会产生很大影响，但却存在阻碍作用，抑制了声波在声学系统中的传播，所以此时预应力模态分析只能反映变幅杆受力之后谐振频率的变化趋势。

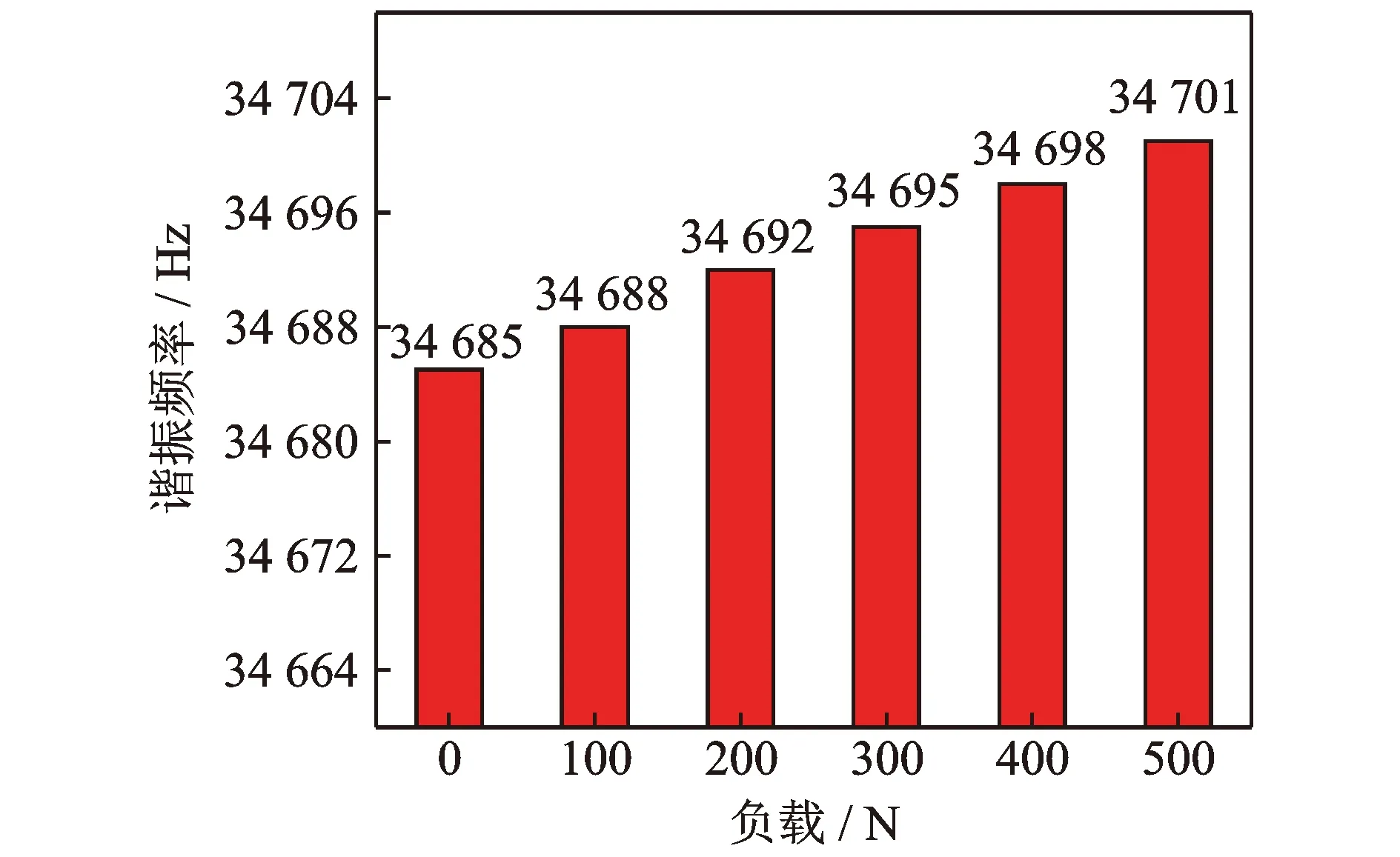
图11 谐振频率随力负载变化图Fig.11 Resonant frequency with force load change diagram

2.5 超声纵-扭复合变幅杆瞬态动力学分析

瞬态动力学分析是时域分析，仿真物体在随时间变化载荷作用下系统的响应过程。

声学系统受力是周期性的，选择5个周期作为分析对象，将一个周期分为两个分析步，一个为力的上升过程，另一个为力的下降过程，共10个分析步。超声钻削声学系统的振动频率为35 kHz，每个分析步时间为1.4×10-5s，选择每个分析步的分析点为10个。参考实际加工时的钻削力，在钻头顶端施加500 N周期变化的轴向压力，在变幅杆左端面施加正弦式变化位移3 μm。分析结果如图12所示。

图12 钻头振幅周期变化图Fig.12 Bit amplitude period change diagram

由图可知，在施加周期力之后钻头振幅随时间的增加呈近似正弦式变化。实际加工中声学系统的温升问题以及动力学分析中的阻尼问题都会进一步影响钻头的振幅，所以在实际情况下钻头受力后振幅不规律变化的现象会更加突出。

3 试 验

3.1 静态模拟力加载试验

模拟试验目的在于模拟加工过程中的受力情况，以及实际加工过程中振幅难以测量的情况。试验设计在万能工具铣床(X8130)上进行，试验装置示意如图13所示。超声振动系统由超声波发生器、无线传输系统、换能器、纵-扭复合变幅杆和钻头组成；在铣床主轴上装夹的工具杆末端开设阶梯孔，一面与钻头相接触，激光位移传感器(Keyence LK-G10)透过孔的另一面测量钻头的振幅。通过升降铣床工作台使工具杆与钻头接触，实现不同负载的施加；测力仪(Kistler-9257B)、电荷放大器(Kistler-5070A)和计算机用于实现负载的精确测量。试验现场如图14所示。

3.2 数据分析

记录不同负载下超声波发生器所追踪的声学系统谐振时的电流和频率值，以及激光位移传感器所测的振幅值，以此分析力负载对系统特性的影响。试验选取3组实际加工中适用的电流值与其对应的谐振频率作变量。试验参数如表3所示。

每个测试点测试3次后取其平均值，每组试验进行3次。采用单因素法，在频率保持不变情况下分别测得负载对电流和振幅的影响情况如图15，16所示。由图15可知，随着负载的增加电流都呈现上

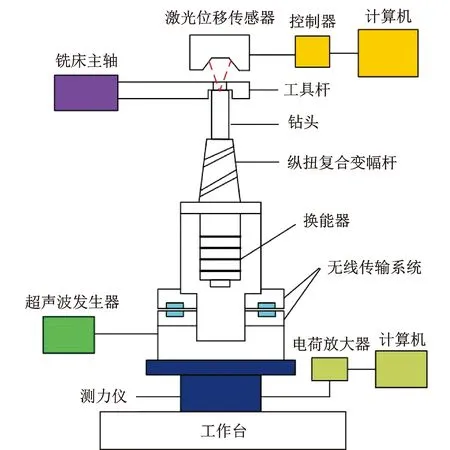
图13 试验装置示意图Fig.13 Test device schematic

图14 力加载试验现场Fig.14 Force loading test site

项目试验参数谐振频率/kHz34.6134.3234.13I/A0.10.20.3

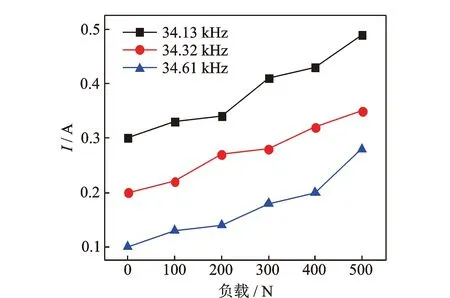
图15 不同频率下负载对电流的影响Fig.15 Effect of load on current at different frequencies

图16 不同频率下负载对振幅的影响Fig.16 Effect of load on amplitude at different frequencies

升趋势，负载为500 N时的电流相较于空载时分别增加63.3%，75%及180%。电流的过大会导致系统处于高损耗、高温度的工作状态，影响系统的稳定性。

由图16可知，振幅随着负载的增加呈现先升高后下降的趋势，当力负载大于400 N后，三者振幅均小于各自空载时的振幅。分析其原因：a.在力增加时，电流迅速增加，系统的输出功率会在短期内快速增加，因此振幅会在前期迅速增大；b.由上文理论推导可知，系统输入阻抗随着负载的增加而增大，系统损耗也随之增大，造成系统能量衰减；且电流的增大会使系统的放大系数减小，所以振幅会在后期逐渐减小；c.当施加的负载过大时，工具杆对钻头振动的抑制也会使得激光位移传感器测得的振幅减小。

按照前述试验方法，保持电流不变，记录不同负载下超声波发生器追踪频率的变化。测得负载对频率的影响情况如图17所示。由图可知，随着负载的增加，谐振频率呈现上升趋势，上升幅度在500 Hz左右，较仿真时有大幅增加。原因为仿真时未考虑系统的温升和超声波发生器自身的追频特性，以及测量过程中的误差。这说明负载的增加会使系统的谐振频率产生偏移，影响系统调谐匹配的过程。

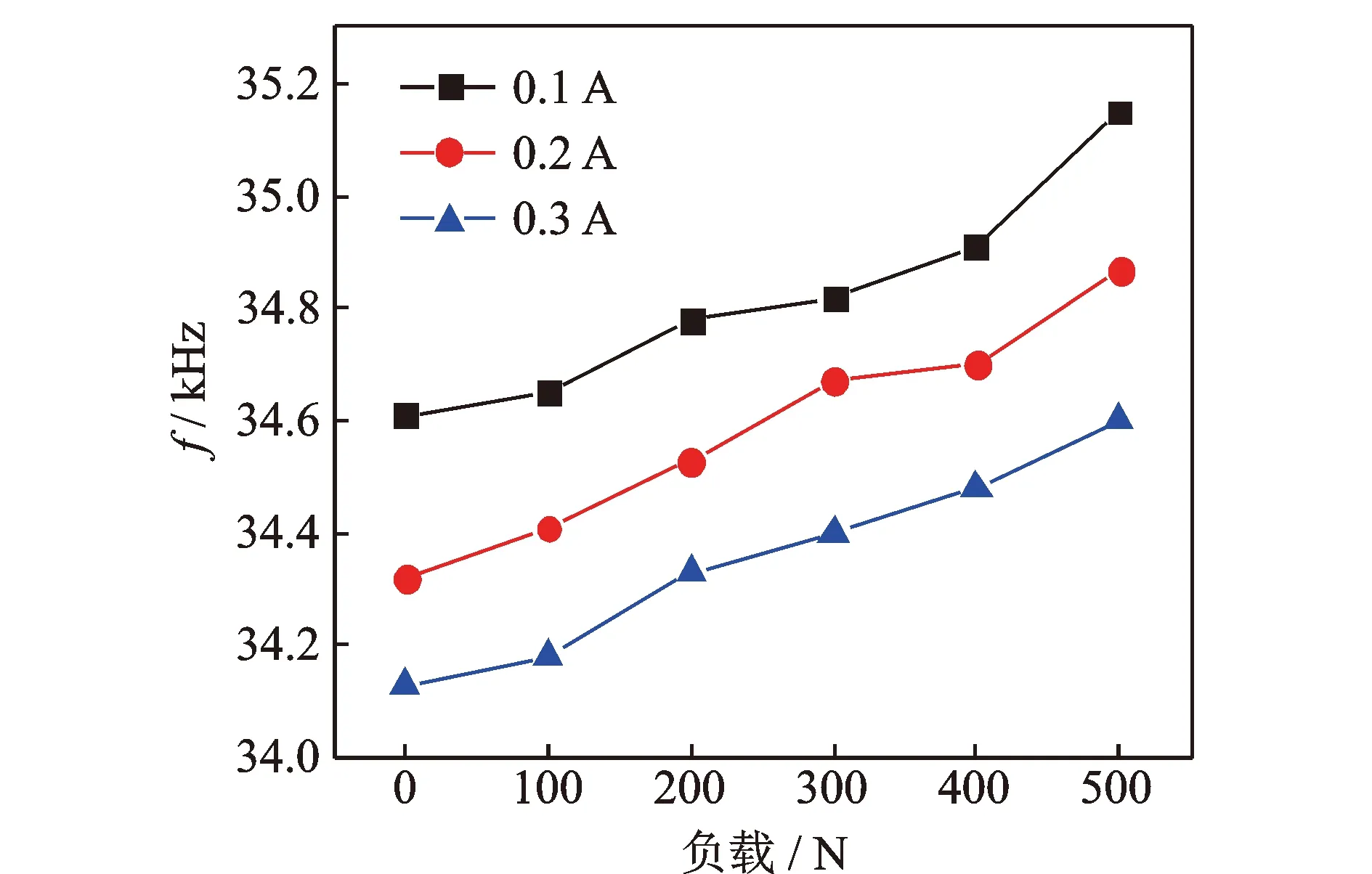
图17 不同电流下负载对频率的影响Fig.17 Effect of load on frequency at different currents

图18 钻削加工试验现场Fig.18 Drilling test site

综上可知，当负载大于400 N后，电流和频率偏移过大，振幅衰减至空载时振幅以下，使声学系统无法正常工作，故实际加工中应避免大负载的出现。

3.3 实际钻削加工试验

试验平台搭建在VMC850E立式加工中心上，工件选用Ti6Al4V钛合金，钻头为直径6 mm硬质合金钻头，试验现场如图18所示。通过虎钳将工件固定在加工中心工作台上，测力仪固定在虎钳下方，超声波刀柄及电磁感应盘固定在主轴上。

分别保持主轴转速和进给速度一定情况下，测得进给速度和主轴转速增加对钻削力的影响如图19所示。频率为34.26 kHz,电流为0.31 A，每组数据测量3次取平均值。

图19 进给速度和主轴转速对钻削力影响图Fig.19 Feed speed and spindle speed influence on drilling force

在给定的试验条件和参数范围内，进给速度每增加5 mm/min，钻削力增加50 N左右。主轴转速每增加500 r/min，钻削力下降40 N左右。可见，进给速度对钻削力的影响略大。

在主轴转速为2 kr/min时，系统谐振频率和电流随进给速度增加的变化情况如图20所示。由图可知，在系统自动匹配过程中保证电流和频率可变的情况下，电流增加了41.9%，频率下降了210 Hz。分别在不同转速、进给速度和超声参数下加工钛合金工件，记录声学系统的工作状态。当电流增幅超过60%、频率变化超过350 Hz时，声学系统会出现明显的失谐现象，超声波发生器无法准确地搜索到系统谐振频率，超声辅助加工效果明显降低。

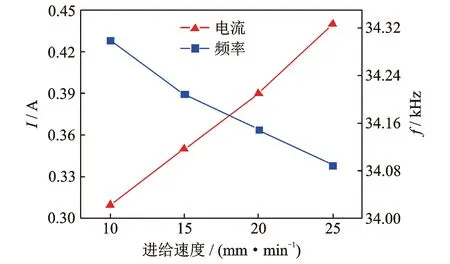
图20 不同进给速度下频率和电流变化情况Fig.20 Frequency and current changes at different feed rates

模拟试验和钻削加工试验表明，力负载变化对系统参数及工作状态影响明显，是导致系统失谐、钻头振幅波动和系统稳定性衰减的主要因素。因此，为使超声辅助作用达到最优，在实际加工中必须合理选择加工工艺和加工参数，以及合理的冷却措施，避免负载大幅度变化及大负载的出现。

4 结 论

1) 通过对整体理论模型进行参数化分析，得出随着力负载的增加，声学系统的输入阻抗增加、电流上升、谐振频率产生偏移，以及系统放大系数减小的结论。

2) 基于有限元仿真，得到谐振频率随静态力增加而升高的变化规律，并发现周期力负载的施加会使系统振幅产生一定波动，其幅度达到13%。

3) 本系统在试验中发现，当力负载大于400 N时，系统谐振时的电流和频率会产生较大偏移，振幅急剧降低。超声辅助钻削钛合金加工中，当电流增幅超过60%，频率变化超过350 Hz时，声学系统会出现明显的失谐现象，从而无法正常工作。在实际加工中应合理选择加工方案和参数，降低力负载对系统稳定性的影响。该结果为研究超声振动系统的稳定性以及超声辅助钻削加工提供了指导和借鉴。