自适应改进双树复小波变换的齿轮箱故障诊断*
2019-11-06陈旭阳韩振南宁少慧
陈旭阳, 韩振南, 宁少慧
(1.太原理工大学机械工程学院 太原,030024) (2.太原科技大学机械工程学院 太原,030024)
引 言
基于各种原因,机械设备采集到的振动信号普遍存在噪声干扰,使得故障特征提取成为故障诊断的重点和难点。离散小波变换在分解过程中的隔点抽样和重构过程中的隔点插零造成的虚假频率成分,易产生较严重的频率混叠,双树复小波变换的频率混叠抑制特性在很大程度上抑制了频率混叠现象的产生,但不能从根本上消除频率混叠现象。因此为了准确提取故障特征,有效地将信号展开,从特定的频率段中识别故障特征,避免频率混叠的方法具有非常重要的意义。双树复小波变换(dual-tree complex wavelet transform,简称DTCWT)是传统离散小波变换的改进方法[1],即用奇、偶滤波器组实现小波的分解与重构,不仅具有传统小波的时频局部化分析能力,而且有离散小波所不具备的抗频率混叠性、近似平移不变性、完全重构性、有限的数据冗余和高效的计算效率等优良性质[2-3]。
Dragomiretskiy等[4]提出一种自适应信号处理方法——变分模态分解(variational modal decomposition,简称VMD)。该方法通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽从而能够自适应地实现信号的频域剖分及各分量的有效分离[5]。摒弃了递归筛分剥离这一信号分解方式的束缚,因此能够有效缓解或避免模态混叠、过包络、欠包络、边界效应等一系列问题,具有较高的运算效率及良好的噪声鲁棒性。
峭度作为分析信号有无故障的指标,是无量纲参数,它与载荷、尺寸、转速等无关,对强冲击故障较为敏感,非常适用于诊断表面损伤类故障。峭度指标绝对值越大的分量中含有故障冲击的成分越多。依据峭度最大原则选取出相关频段信号做分析,可以有效地检测到瞬态信号。峭度指标绝对值越大,故障越严重。
本研究将双树复小波变换与变分模态分解(dual-tree complex wavelet transform-variational mode decomposition,简称DTCWT-VMD)结合,提出了一种改进双树复小波变换方法,将其应用于齿轮箱振动信号故障特征提取。由于采用变分模态分解将双树复小波变换得到的窄带信号进行自适应分解,从根本上消除了频率混叠现象,提高了信号分解的信噪比和频率选择性。仿真和实验分析结果表明,该方法能有效地消除频率混叠现象,减少频率干扰,有效识别故障特征。
1 基本理论
1.1 双树复小波变换
双树复小波变换采用二叉树结构的两路滤波器组进行信号的分解和重构,一树生成实部,一树生成虚部,合理设计实、虚部树低通滤波器,满足半采样延迟条件,具有近似平移不变性。两树滤波器采样频率相同,但是它们之间的延迟恰好是一个采样间隔,这样虚部树中第1层的二抽取恰好采到实部树中二抽取所丢掉的采样值,在获得了复小波变换的平移不变性的同时避免了大量的计算并且具有容易实现的优势。
图1所示为3层双树复小波分解和重构过程。
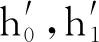
小波函数表示
ψ(t)=ψh(t)+iψg(t)
(1)
其中:ψh(t),ψg(t)为两个实小波;i为复数单位。
图1中,虚线上方实部树变换的小波系数和尺度系数可由式(2)和(3)计算
(2)
(j=1,2,…,J)
(3)
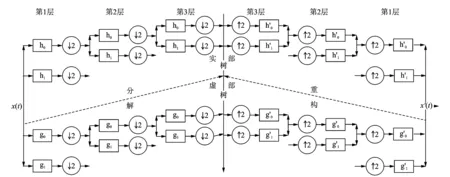
图1 双树复小波变换分解和重构Fig.1 Decomposition and reconstruction of double-tree complex cavelet transform
同理,下方虚部树变换的小波系数和尺度系数可由式(4)和(5)计算
(4)
(j=1,2,…,J)
(5)
因此,可得到双树复小波变换的小波系数和尺度系数
(6)
(j=1,2,…,J)
(7)
最后,双树复小波变换的小波系数和尺度系数可由式(8)和(9)重构
(8)
(9)
双树复小波变换后的重构信号可表示为
(10)
1.2 变分模态分解
VMD的目标是基于经典维纳滤波-希尔伯特变换和混频的变分问题,根据信号自身的频域特性完成频带的划分,并将其分解为指定个数的本征模态函数分量,在再现输入时具有特定的稀疏特性。该方法在获取分解分量时通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽从而能够自适应地实现信号的频域剖分及各分量的有效分离[5-7]。在信号分解精度和噪声鲁棒性方面具有明显优势,但需预先确定模态数k,而目前k只能靠先验知识进行预估。如果预估的k与实际信号存在差异,会导致分解误差较大。
假定将原始信号分解为k个IMF分量,则对应的约束变分模型表达式[8]为
(11)
其中:{uk}={u1,…,uk}为分解得到的k个IMF分量;{ωk}={ω1,…,ωk}为各分量的频率中心。
为求上式约束变分的最优解,引入如下增广Lagrange函数,即
L({uk},{ωk},λ)=
(12)
其中:α为惩罚参数;λ为Lagrange乘子。
利用交替方向乘子算法ADMM更新以上参数和求取上述增广Lagrange表达式式的鞍点[9]。具体实现步骤如下:
2) 执行循环:n=n+1;
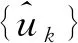
(13)
4) 更新ωk
(14)
5) 更新λ
(15)
6) 重复步骤(2)~(5),直到满足迭代停止条件
(16)
结束迭代,得到k个IMF分量。
1.3 粒子群优化
不同于进化类算法的复杂遗传因子的过程,粒子群优化算法采用速度-位移模式进行全局优化搜索。同时继承人工智能的记忆特性,可以根据当前最好的那个粒子位置及时调整搜索策略,是一种高效的搜索算法[10]。
粒子群算法的思想来源是鸟群觅食的群体共享机制模拟。每个粒子都是解空间中的一个解,根据自己和同伴的经验随时改变自己的速度和位置从而到达目标地点。每个粒子的最优解即个体极值为pb,而整个群体的最优解即全局极值为gb,每个粒子都是通过pb和gb随时调整自己的位置和速度。改变位置和速度的公式为
Vi(t+1)=ωVi(t)+c1rand(pbi-xi(t))+
c2rand(gb-xi(t))
(17)
Xi(t+1)=xi(t)+Vi(t)
(18)
具体步骤为
1) 初始化各粒子的速度和位置。
2) 确定一个适应度函数,适应度函数为双树复小波分解各分量的峭度最大值。
3) 比较粒子个体与种群的适应度值,粒子中峭度值最大的粒子为个体最优值,种群中峭度值最大的粒子为种群最优值。
4) 通过式(17,18)更新粒子的速度和位置。i表示第i个粒子,t表示迭代次数,rand为[0 1]上的随机数,c1,c2为学习因子。一般情况下,种群规模t取10次,视问题的复杂程度而定;ω取0.4~1;c1和c2都取1.0。每次更新位置时计算一次适应度值。
5) 计算粒子和种群的适应度值,与前一步中的个体和种群最优值进行比较,更新个体和种群最优值。判断新种群是否达到终止条件即各层分解后各分量的峭度最大值所对应的分解层数,达到则执行步骤6,否则继续执行步骤4。
6) 退出迭代,输出全局最优值(即峭度最大值所在的分解层数)。
2 实施流程
2.1 实施步骤
1) 通过粒子群寻优,寻找最优分解层数。
2) 双数复小波分解并分别对低频、高频分量进行单支重构。
3) 对各重构后高频分量分别进行变分模态分解,并通过最大峭度值寻找各高频分量经过分解后的主频分量。
4) 分析双数复小波分解并单支重构后的低频分量以及经过上述步骤处理后的各高频分量的频谱图。
5) 分别与只进行双树复小波分解以及只进行变分模态分解后的频谱图对比,并得出结论。
2.2 流程图

图2 流程图Fig.2 Flow chart
3 仿真结果分析
构造如下齿轮局部故障仿真信号验证本方法的可行性和有效性,调制-载波信号的表达式
x(t)=(|sin(100πt)|+|sin(200πt)|)·
|sin(400πt)|
(19)
图3为该信号波形图和频谱图。图4为上述仿真信号各分量信号单独的波形图和频谱图。
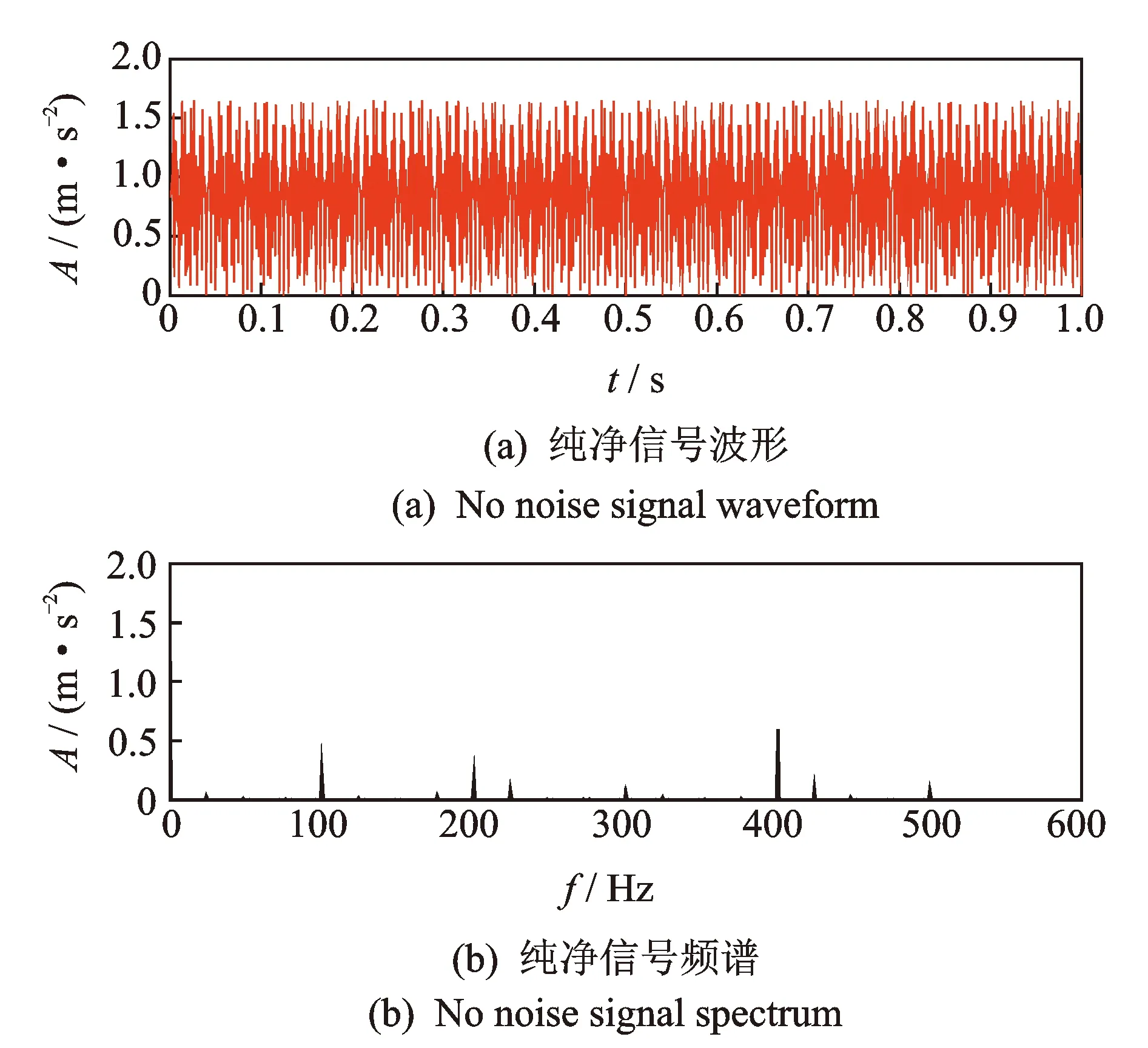
图3 仿真信号波形及频谱Fig.3 Simulation signal waveform and spectrum
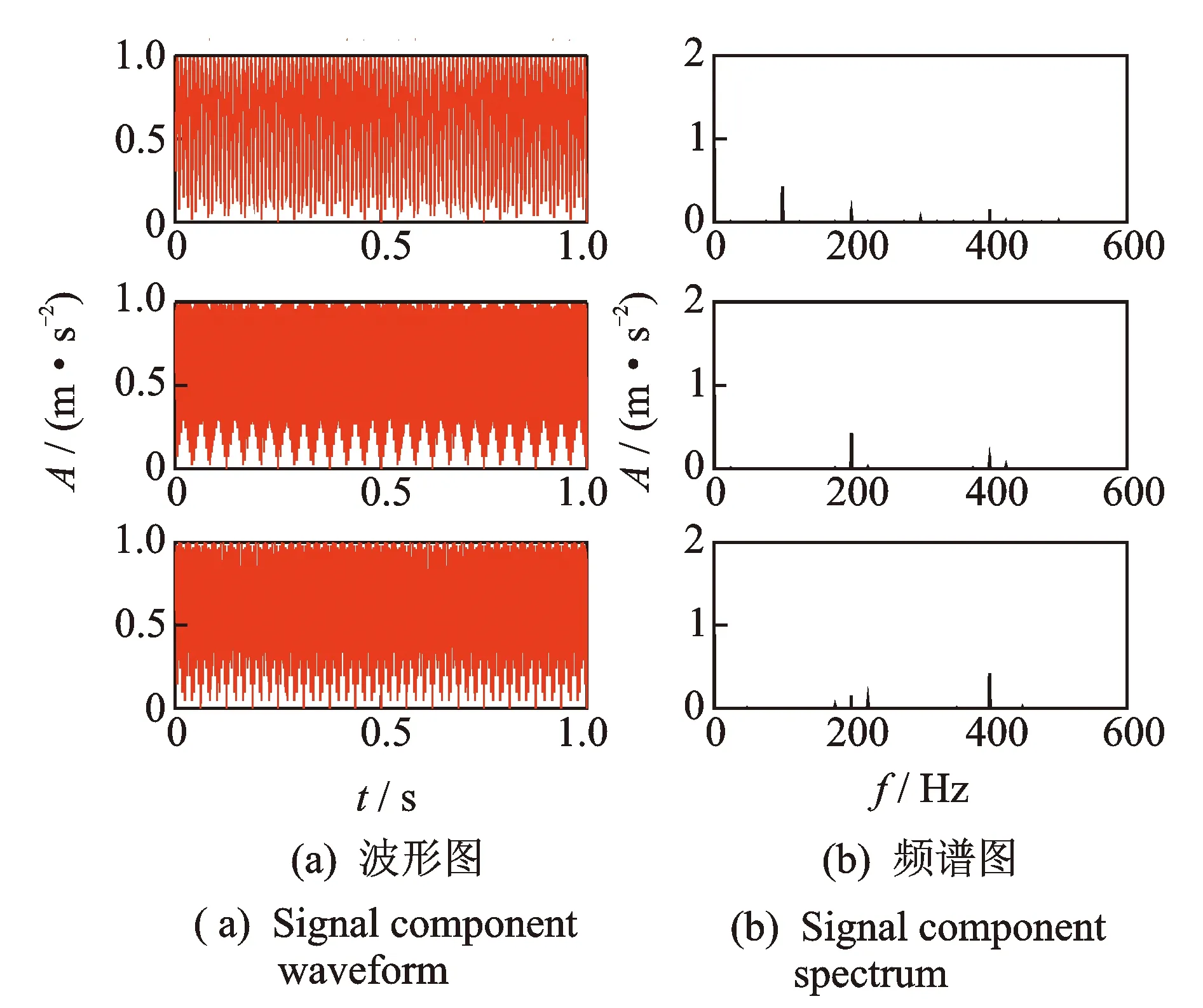
图4 各分量信号波形及频谱Fig.4 Each component signal waveform and spectrum
图5为信号经过双树复小波三层分解后的各分量信号的波形图和频谱图。从图中可以看出,分解后得到的信号分量比较接近图4原仿真信号各分量波形,但是b2和b3分量存在频率混叠现象,而且在b2,b3中有邻带频率成分,分解效果不是很理想。
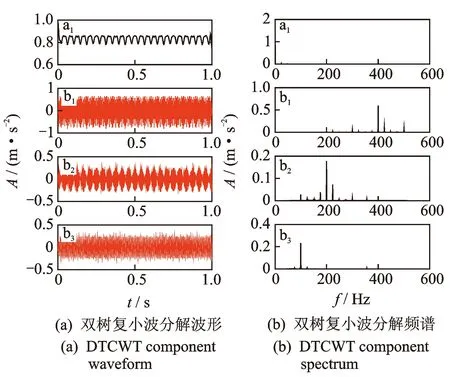
图5 双树复小波分解各分量波形及频谱Fig.5 Double wave complex wavelet decomposition of components and spectrum
图6为用VMD方法分量个数k取3分解得到的波形图和频谱图,从波形图可以看到分解效果不理想,和图4原仿真信号的波形相差较大。
图7为用本方法经双树复小波各高频分量经过变分模态分解后用最大峭度值提取出的最佳分量的波形及频谱图,从图中可以看出分解效果非常理想,基本没有频率混叠现象,消除了双树复小波会产生的奇行波以及邻带频率现象。
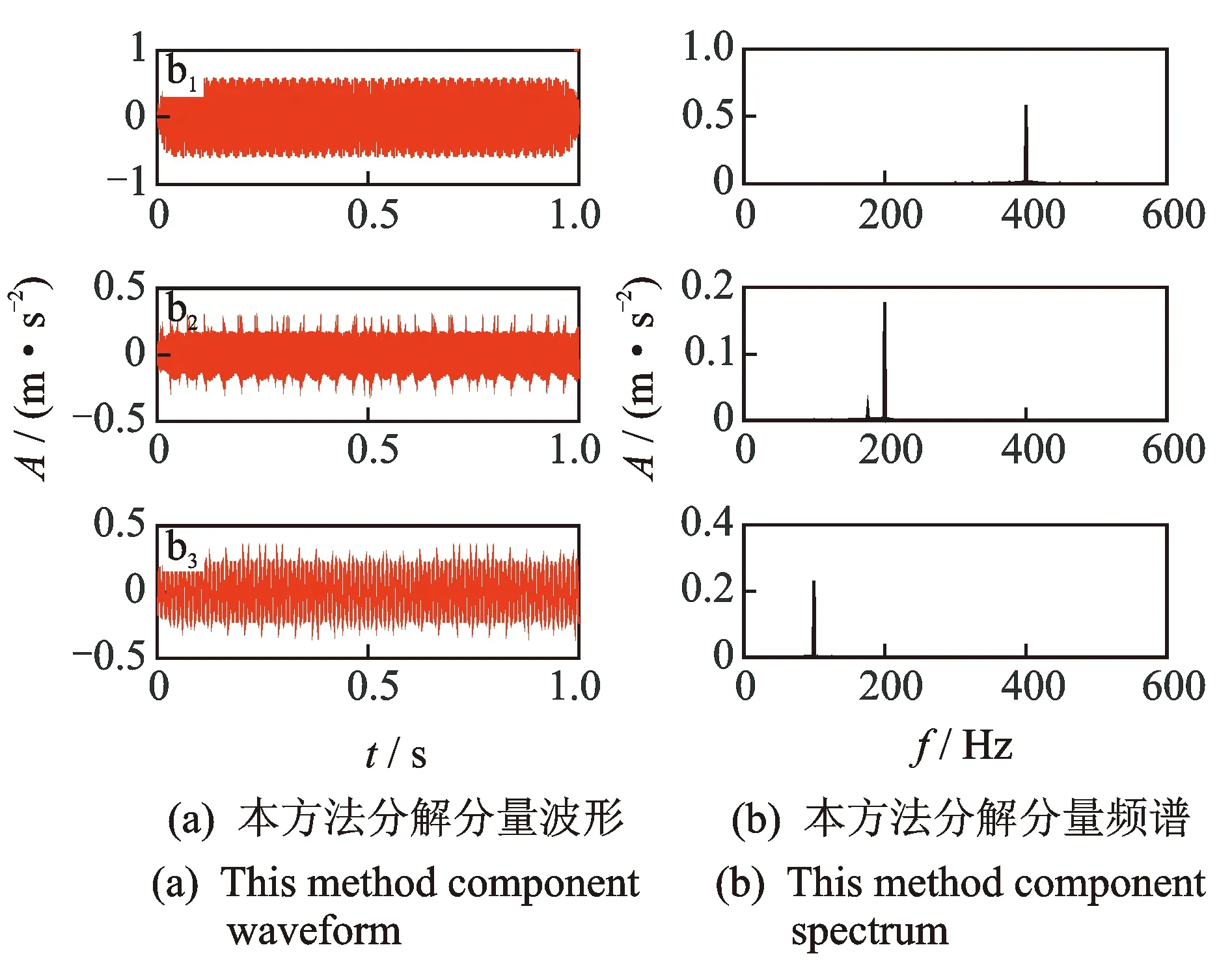
图7 DTCWT-VMD分解各分量波形及频谱Fig.7 This method decomposes the components of the waveform and spectrum
4 实验结果分析
笔者设计试验台通过扭力杆产生的内力进行加载,转速用电动机进行调节。实验齿轮的传动比为 1∶1,采取半齿啮合,图8为本研究实验台。

图8 实验台Fig.8 Test stand
粒子群寻优过程中峭度值随种群进化代数的变化见图9,图中为适应度曲线,终止次数为10。从图中可以看出3层以后的峭度最大值趋于定值。本研究采用3层为最优分解层数。

图9 适应度值随分解层数的变化Fig.9 The change of the fitness value with the number of decomposition layers
设计电动机转速保持在1 200 r/min左右,扭矩为800 N左右,采样频率为12 000 Hz,啮合频率为210 Hz,通过传感器,信号采集仪采集到的无故障实验信号波形图、频谱图和包络谱图如图10所示。
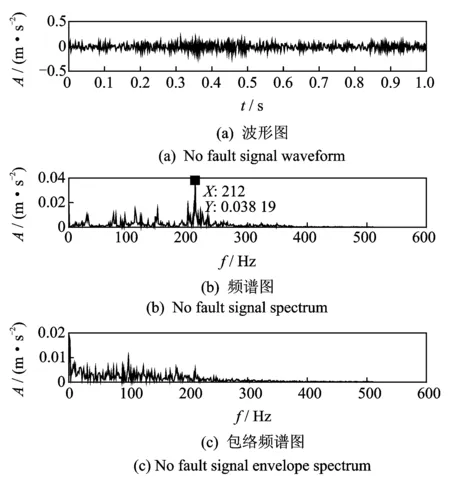
图10 无故障信号波形及谱图Fig.10 No fault signal waveform and spectrum
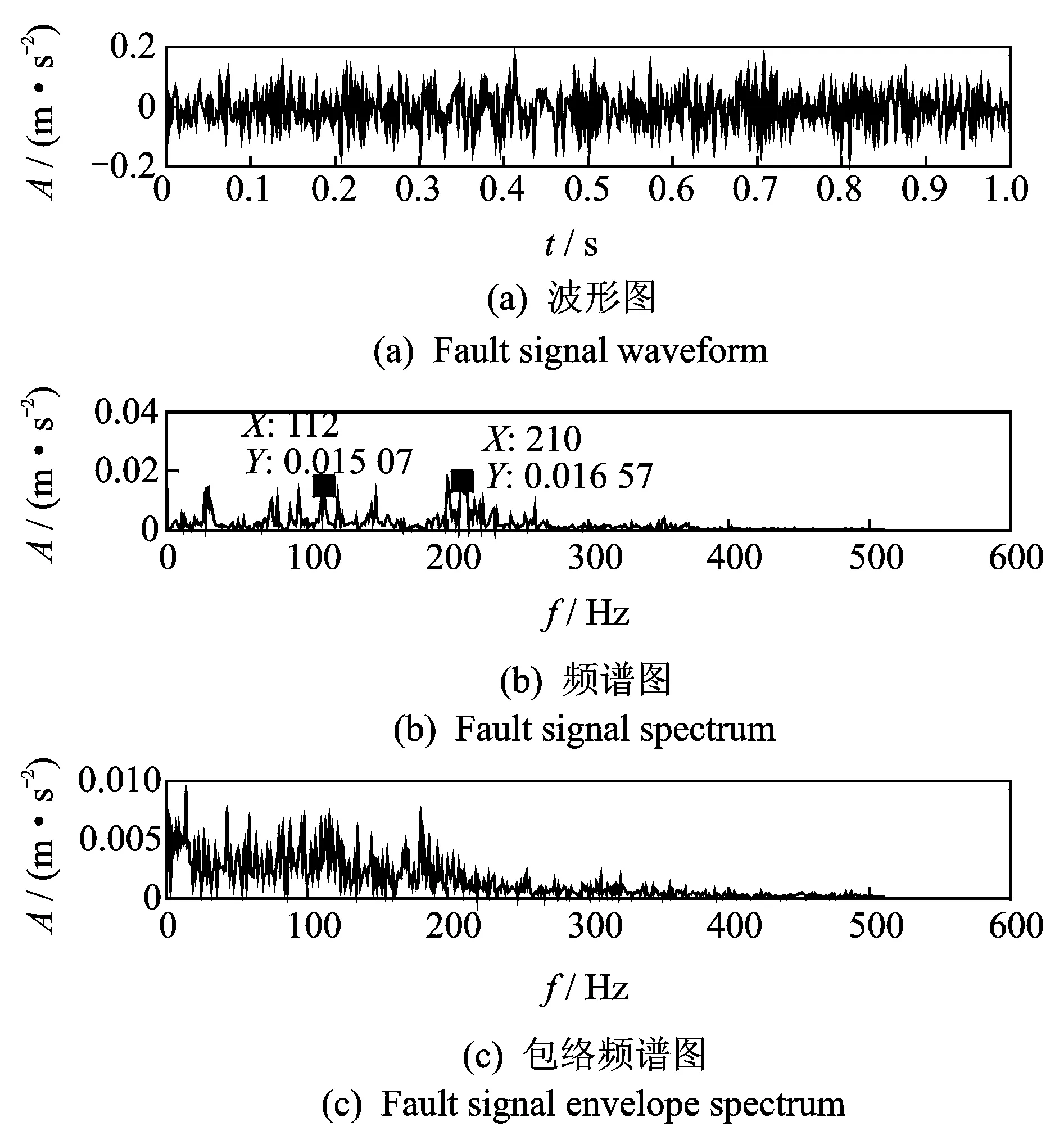
图11 故障信号波形及谱图Fig.11 Fault signal waveform and spectrum
图11为电动机转速保持在1 200 r/min左右采集的有故障的实验信号,由于故障信号(齿轮点蚀)比较微弱,而且淹没在强背景噪声下,从频谱图中看出存在边频成分和干扰成分。可以看出当齿轮出现点蚀时,出现了啮合频率和半频的边频成分,其幅值不均一,正常齿轮频谱在110和210 Hz处有明显峰值。
图12为信号经三层双树复小波分解得到的信号的波形图及频谱图,啮合频率出现在b2分量中,半频110 Hz出现在b3分量中,倍频的各次谐波出现在b1高频分量中。较好的分离出齿轮的啮合频率及半频。但是在高频分量b1和b2以及b3中可以看出存在频率混叠现象,存在严重的邻带频率现象。
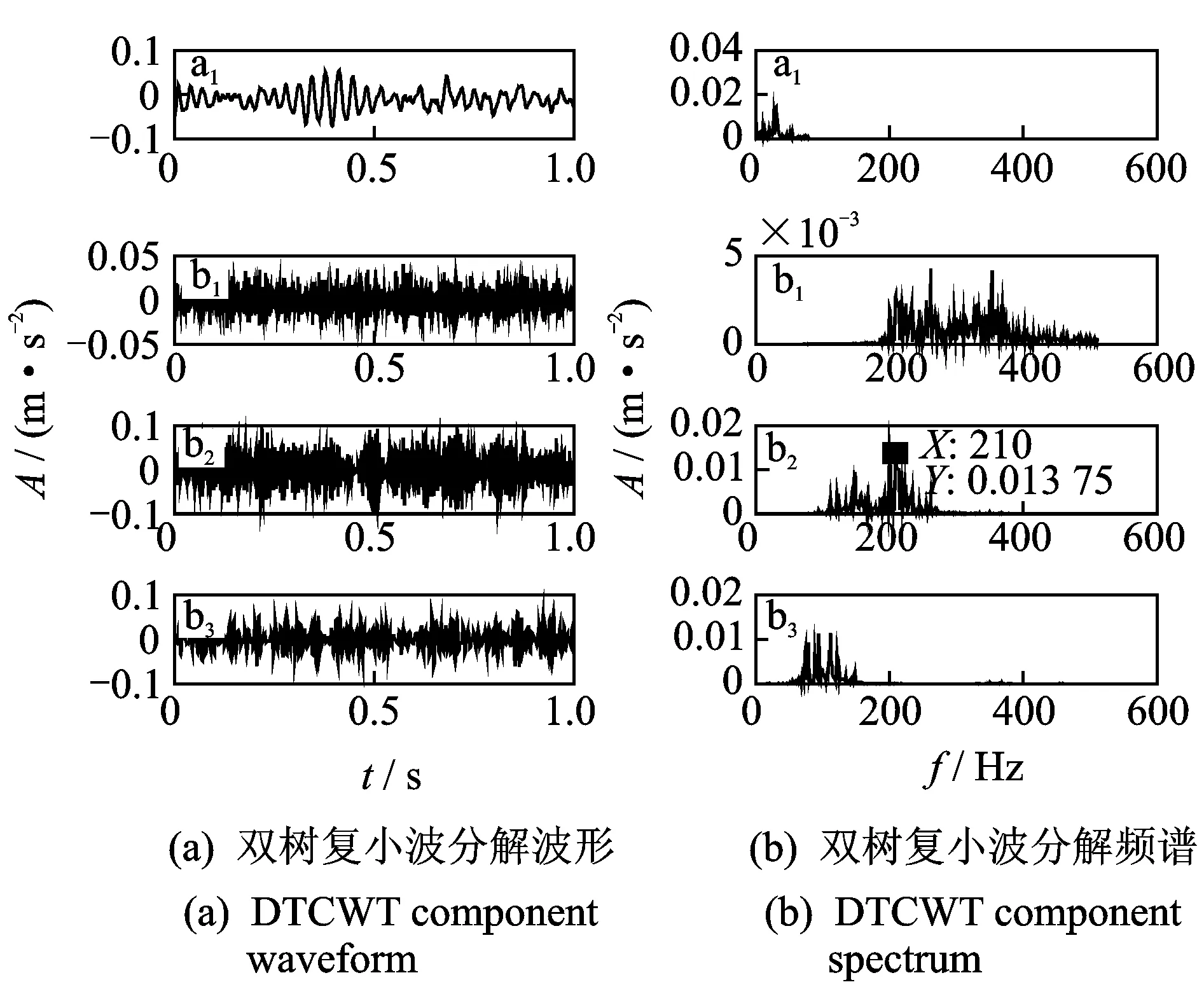
图12 故障信号经双树复小波分解波形及频谱Fig.12 Wavelet decomposition waveform and spectrum of fault signal by double tree complex vavelet
图13为信号经VMD分量个数k取3所得波形及频谱图。从图中可以看出虽然不存在频率混叠现象,但是丢失了啮合频率半频成分,分解效果不理想。
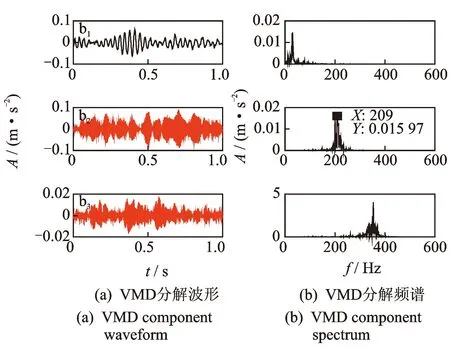
图13 故障信号经VMD分解波形及频谱Fig.13 Wavelet decomposition waveform and spectrum of fault signal by VMD
图14为本方法(DTCWT-VMD)对故障信号经双树复小波分解各高频分量再进行三层VMD分解所得各个峭度值最大分量的波形及频谱图(只是处理后的各高频分量频谱图)。从图中可以看出很好地分离出了啮合频率及半频成分以及倍频的各次谐波,而且不存在频率混叠现象。通过与图14对比可以看出,分解效果理想。从b1和b3分量中存在边频成分且从图12中看出出现边频成分,且本方法处理后的干扰频率较少,验证了本方法的可行性和有效性。
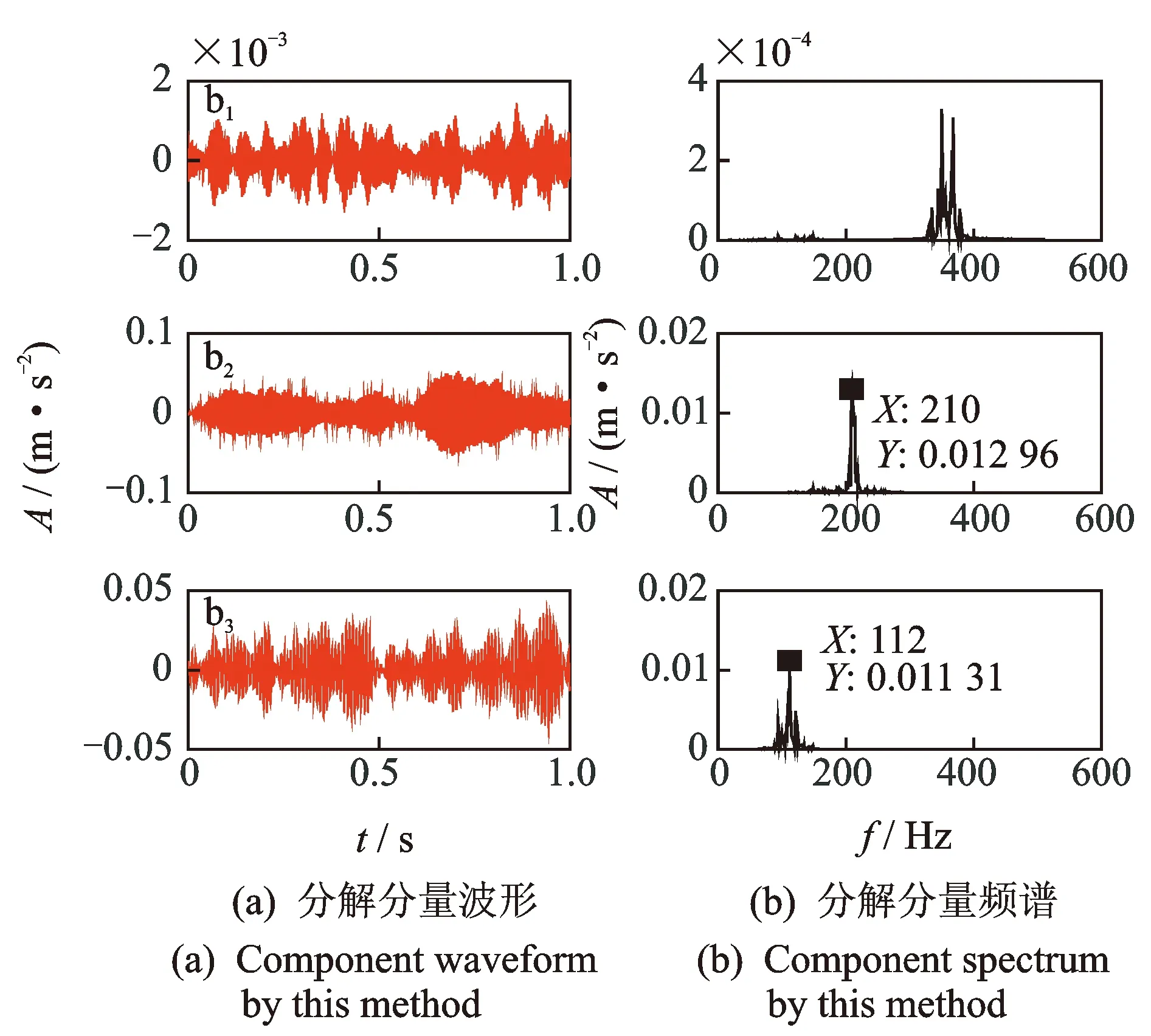
图14 故障信号经本方法分解波形及频谱Fig.14 Wavelet decomposition waveform and spectrum of fault signal by this method
5 结束语
为了克服双树复小波变换产生频率混叠的缺陷,提出了改进双树复小波变换的故障诊断方法。由于双树复小波分解不同分解层数会影响分解效果,分解层数少则分解效果不理想容易丢失有用信息,而分解层数太大则容易频率混叠,因此将峭度值作为适应度函数,通过粒子群选择最优分解层数。仿真和实验信号结果表明,与双树复小波分解及VMD分解效果相比,该方法不仅能够消除信号处理中频率混叠现象,提高了信噪比和频带选择的正确性,而且还提高了从强噪声环境中提取瞬态冲击特征的能力。
