一种新的摆度信号去噪方法及其应用*
2019-11-06贺生国杨清勇高炳春雷延科
刘 勇, 贺生国, 杨清勇, 高炳春, 刘 鹏, 雷延科
(1. 湘潭大学信息工程学院 湘潭,411105) (2. 广西桂茂电力有限责任公司 河池,546300)
引 言
水电机组的摆度是衡量机组运行稳定性的重要指标之一,其包含了丰富的机组运行信息。在水电机组测试过程中由于现场环境和设备的干扰不可避免地引入各种噪声,这对机组的安全运行和后续的故障诊断十分不利[1-2]。因此,迫切需要一种准确、快速滤除噪声的方法,才能获得真实有效的信息,从而获得可靠的分析结论。
小波分析具有良好的时频局部性能和多分辨率分析的特性,特别适用于分析突变和非平稳信号,已广泛应用于振动信号的处理[3-5]。基于小波变换的阈值法因其计算量小、实现方便而应用广泛。然而,机组摆度信号采集现场环境较为复杂,由传感器采集得到的信号包含大量噪声,其中以白噪声和脉冲噪声最为常见。小波阈值去噪法可以很好地抑制白噪声,但对脉冲噪声抑制效果不佳[6]。传统小波阈值去噪方法只对小波分解后的细节系数进行处理,并没有考虑近似系数对重构后信号的影响,其去噪性能还有待提高。
中值滤波是一种非线性滤波方法,其抑制脉冲噪声的能力强,同时又能保护信号边缘的有效复原[7]。Savitzky-Golay滤波被广泛应用于数据流平滑去噪,其最大的特点在于滤除噪声的同时可以确保信号的形状、宽度不变[8]。因此,笔者考虑将小波阈值去噪、中值滤波以及Savitzky-Golay滤波方法相结合,提出了中值-小波平滑去噪方法。该方法首先对待分析信号进行中值滤波处理,在最大程度保持原始信号特征的前提下抑制脉冲噪声及部分白噪声的影响;对小波分解后的各层细节系数和最后一层近似系数分别进行阈值降噪和Savitzky-Golay滤波,这样既能保持信号的高频特征部分,又可以有效保持信号低频部分的平滑特性。
对小波阈值去噪、中值滤波、中值-小波去噪以及本研究去噪方法进行了仿真分析。结果表明,新方法在均方根误差、局部相关指数、信噪比以及平滑度上均优于其他3种方法。最后,将新方法成功应用于水电机组摆度信号提纯,验证了该方法在提纯机组摆度信号的有效性以及优越性。
1 去噪预处理原理
1.1 小波阈值去噪原理及其去噪性能分析
假设一维含噪信号模型为
y(n)=x(n)+δ(n) (n=1,2,…,N)
(1)
其中:x(n)为原始信号;δ(n)为噪声信号;y(n)为含噪信号。
对信号y(n)进行小波消噪,就是对小波分解后的系数进行切削、阈值处理、缩小幅值范围来分离信号及去噪的过程,其具体步骤如下。
1) 小波分解。选取合适的小波基并确定分解层数L,对含噪信号y(n)进行小波分解,其分解公式为
(2)
其中:cL,K和dL,K分别为小波分解后的近似系数和细节系数;h,g为滤波器脉冲响应;N为采样点数。
2) 阈值选取和量化。选取合适的阈值函数及阈值对分解后各层细节系数进行阈值化处理。阈值函数包括软阈值函数和硬阈值函数两种[6],其中硬阈值函数形式为
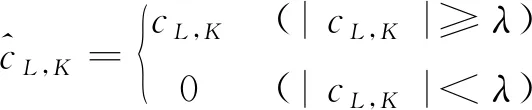
(3)
硬阈值处理是以设定的阈值为界限,大于阈值的点保存不变,而将信号的绝对值小于或等于阈值的点变为零;软阈值处理是将小波分解后各层细节系数的绝对值与设定的阈值进行比较,当数据的绝对值小于或等于阈值时,令其为零,大于阈值的数据点则变为该点值与阈值的差值,即
(4)
其中:sign(x)为符号函数,若x>0,则返回1;若x=0,则返回0;若x<0,则返回-1。
3) 小波重构。利用式(5)对经阈值处理后的各层细节系数和未经处理的近似系数进行重构,即得到消噪后的信号。
cL-1,n=∑cL,nhK-2n+∑dL,ngK-2n
(5)
由上述分解过程可知,小波阈值去噪方法对白噪声具有很强的抑制效果,因为白噪声的能量分布在整个小波域,而有用信号的大部分能量只集中于低尺度的若干系数中,在小波系数上表现为分解后有用信号的幅值大于白噪声的幅值,根据有用信号和白噪声这一不同特性就可以对信号进行阈值降噪处理[6]。然而,对于脉冲噪声,其能量也主要集中于小区域范围上,其分解后的细节系数不能满足远远小于有用信号的小波变换系数的条件。所以,当阈值选取过小时,经阈值处理后的细节系数仍包含较多的噪声成分;若阈值取得太大,经处理后的细节系数则丢失了原始信号的某些特征[9]。因此,对于含有脉冲噪声的信号,直接对其进行小波阈值去噪处理的效果不理想,有必要对其进行预处理。
在进行小波分解之前,首先要确定小波分解层数。分解层数的选取需要兼顾小波细节系数序列的层数以及小波近似系数序列的平滑特性。当分解层数过少时,最后一层近似系数序列中仍含有大量白噪声分量,信噪比得不到很大的提高;当分解层数过多时,虽然最后一层近似系数序列更加平滑,但需要采用阈值处理的细节系数序列的层数也越多,这会造成有用信号的丢失,使得重构后的波形产生畸变,信噪比反而降低。为了最大程度保持原始信号的形态特征,往往牺牲了近似系数序列的平滑特性。因此,可以通过对近似系数进行平滑处理,以进一步提高信噪比。
1.2 中值和Savitzky-Golay滤波
中值滤波是一种非线性处理技术,其对平滑噪声的抑制能力较差,但对满足一定脉宽条件的脉冲噪声抑制能力强[10-11]。对于小波分解后的细节系数的处理,大多数文献均采用阈值降噪的方法。因为细节系数是以噪声信号为主导的,其包含了大量的白噪声,应用阈值处理的方法能达到很好的抑制效果。此外,通过研究发现,Savitzky-Golay滤波方法对小波近似系数降噪效果较好,因为近似系数是以低频有用信号为主导的,经Savitzky-Golay滤波处理,可以使信号变得更平滑,同时可以有效保持原始信号的形态特征。因此,本研究考虑将小波阈值去噪、中值滤波以及Savitzky-Golay滤波方法有机结合,形成一种中值-小波平滑综合去噪方法,可以在有效滤除噪声的同时保留信号的全局和局部特性。
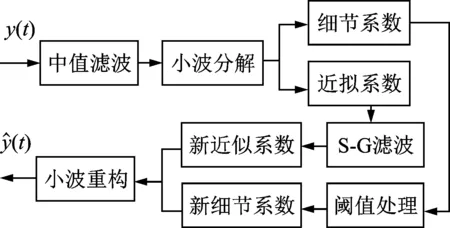
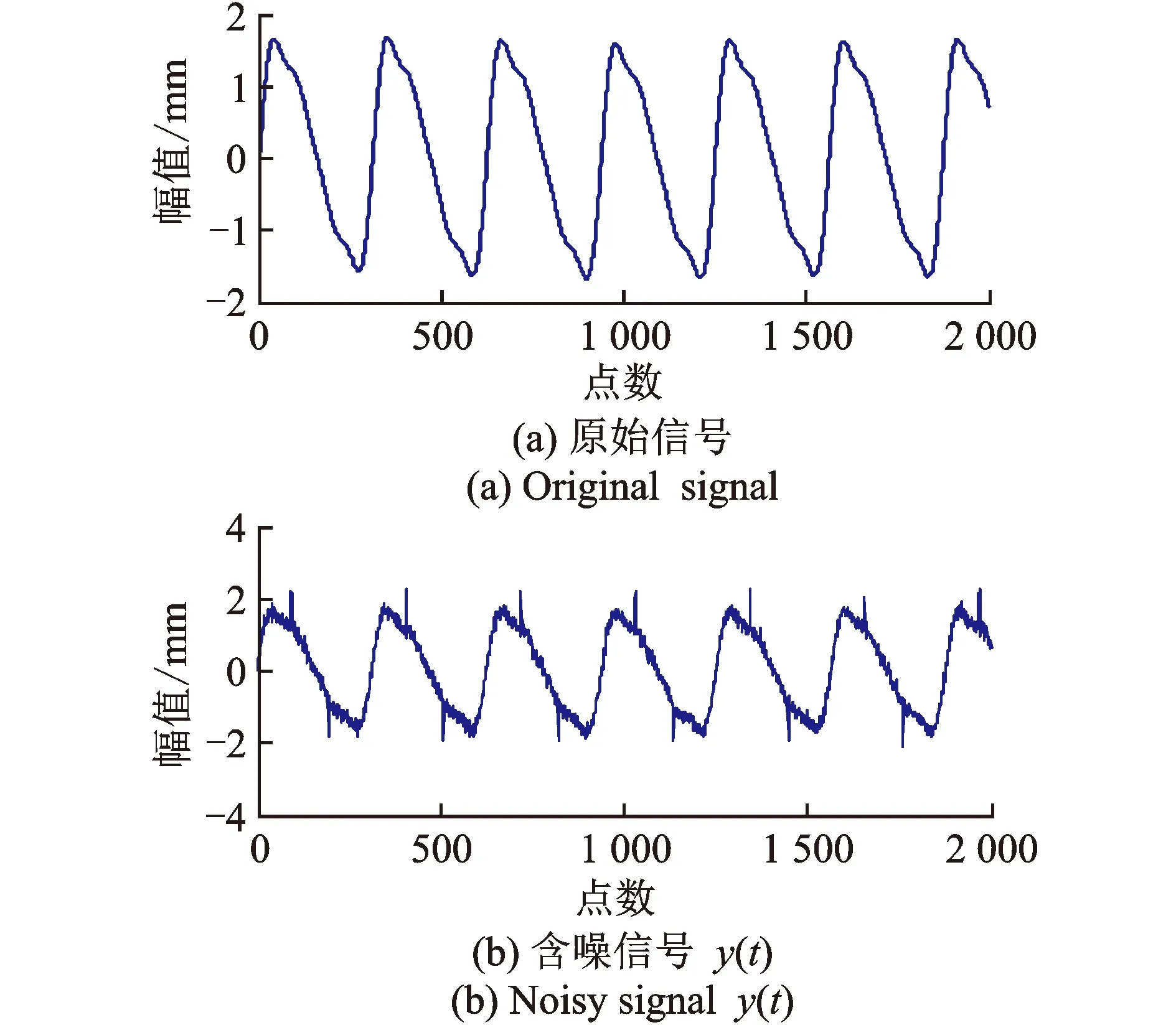
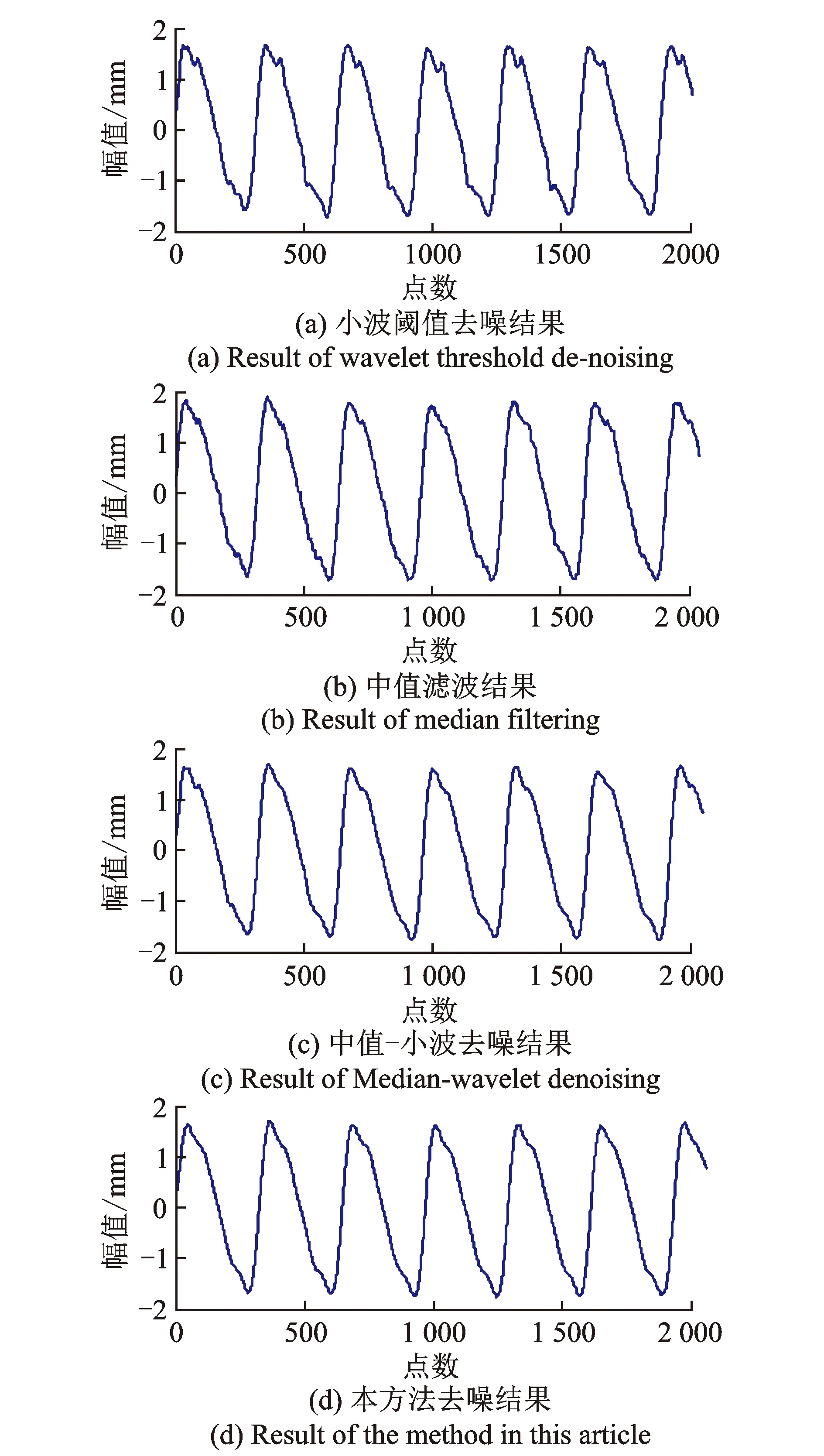
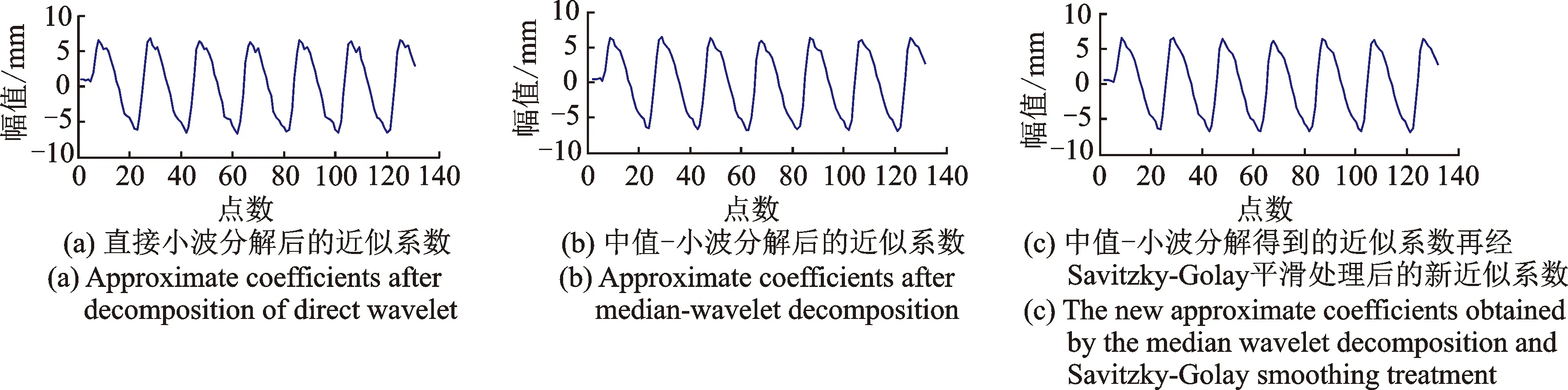
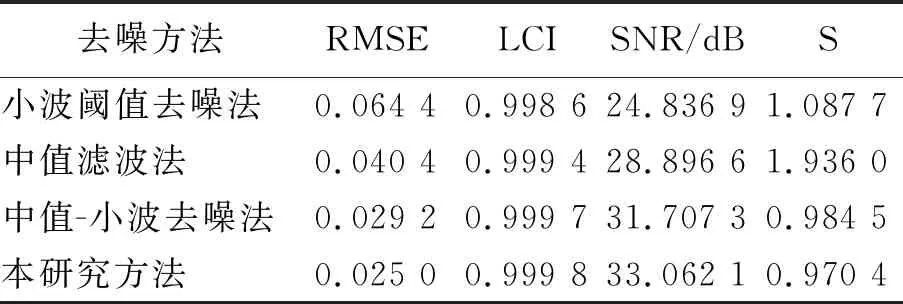
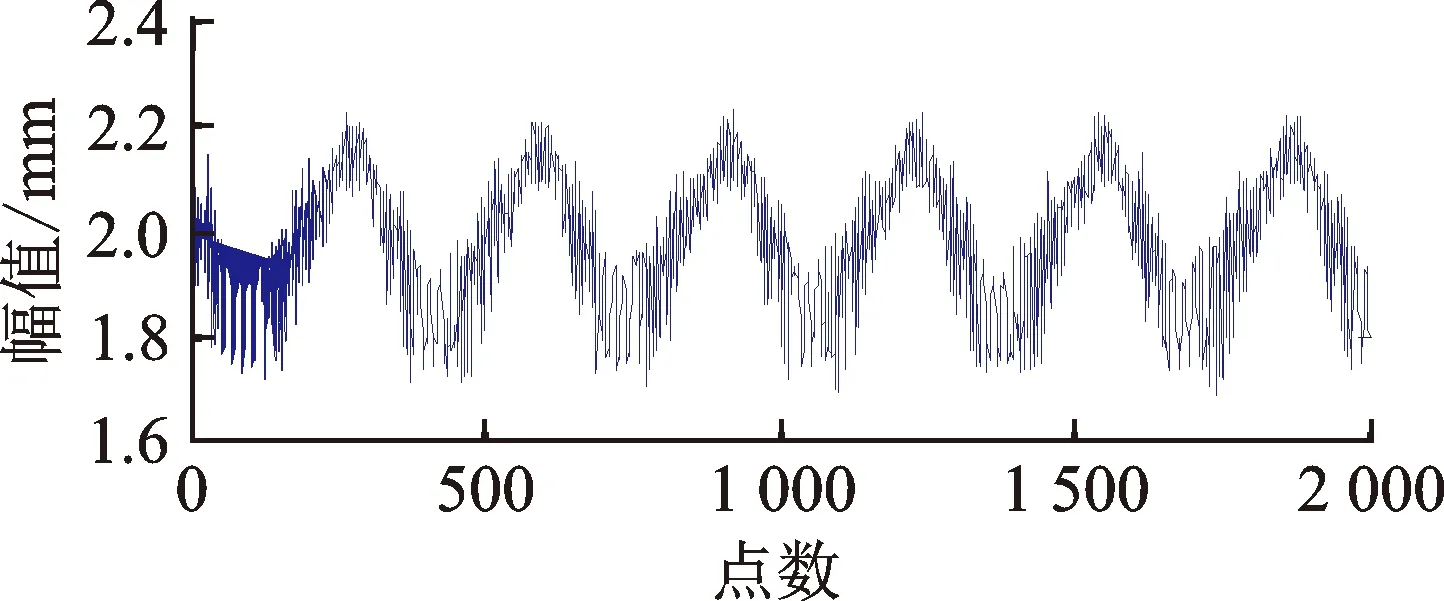
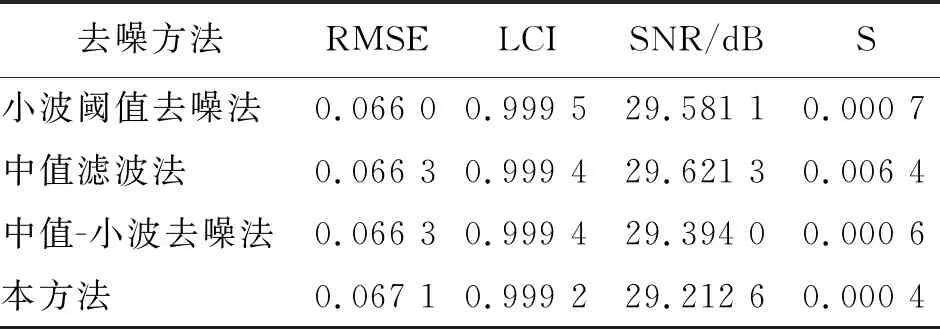
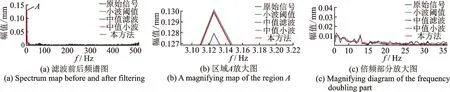
中值滤波的基本原理是把数字序列中任一点的值用该点邻域内各点的中值来代替[12]。假设xn(n=1,2,…,N)为待中值滤波处理的一维序列,设定滤波窗口长度为M。从xn中抽取相邻的长度为M的样本序列x1,x2,…,xM,将该样本序列从小到大排序后得x(1) (6) 其中:median(x)为取中值函数。 将滤波窗口沿着序列xn向右移动,即得到整个滤波后的序列。为了使滤波输出序列的长度与输入序列长度一致,滤波前需在输入序列两端各扩展k个点。可采取每边扩展的k个信号值都与各自两端的信号值相对应的方法[7],也可都取为0,即 (7) 其中:k=M/2,M为偶数;k=(M-1)/2,M为奇数。 滤波窗口长度的选取是中值滤波算法的关键。窗口长度较大时,滤除脉冲噪声效果越明显,但会损失真实有效信号;窗口长度较小时,可以较好的保持原始信号特征,但却降低了脉冲噪声的去除效率。实际应用中,应根据信号中待提取信号的形态特征来选定滤波窗口的长度。本研究通过对模拟数据以及现场采集的数据进行从小窗口到大窗口的中值滤波试验,最后从中选取滤波效果最佳时所对应的窗口长度。 Savitzky-Golay滤波是一种在时域内基于局域多项式最小二乘法拟合的滤波方法,其最大的特点为滤除噪声的同时可以确保信号的形状、宽度不变。对于一维信号的处理,Savitzky-Golay算法可作如下描述[8]。 (8) 最小二乘拟合的残差为 (9) 当式(9)取得最小值时拟合效果最好。令其对多项式系数的偏导数为0,即 (10) 整理后得 (i=1,2,…,N) (11) 引入(2m+1)×(k+1)维辅助矩阵A={ai,j},其中ai,j=ij, -m≤i≤m,0≤j≤N。再设矩阵B=ATA,则有 (12) 从而 Ba=ATAa=ATx (13) a=(ATA)-1AT=Hx (14) 矩阵H的第1行即为所求的卷积系数。 图1 中值-小波平滑滤波方法的基本流程Fig.1 The basic process of median wavelet smoothing filtering method 1) 均方根误差(mean square error,简称RMSE) (15) 2) 局部相关指数(local correlation index,简称LCI) (16) 3) 信噪比(signal noise ratio,简称SNR) (17) 4) 平滑度(smoothness,简称S) (18) 评价标准定义为:若消噪后的信号的RMSE值、S值越小以及LCI值、SNR值越大,则表明它更接近于原始信号,去噪效果越好。 工程实际中,由传感器采集到的水电机组摆度信号中的有用成分通常表现为低频信号或平稳信号,其分量一般为机组的转频及其倍频和几个固定频率。文中用0.25,0.5,1,2,3,4倍转频再加上噪声来模拟现场采集的机组摆度信号 y(t)=x(t)+n(t)+w(t) (19) 采样频率为1 kHz,采样2 000个点。原始信号x(t)波形以及叠加噪声后y(t)波形分别如图2(a),(b)所示。用不同方法对含噪信号进行处理,其中小波基函数选择较常用的db4小波,分解层数为4层,中值滤波窗口长度取13。分解层数和滤波窗口长度是通过对模拟数据多次实验,最后选取4个性能指标最优时所对应的分解层数和窗口长度。采用不同方法去噪结果如图3所示。 图3(a)为信号直接小波阈值去噪结果。从图3(a)可以看出,经小波阈值去噪后,信号中的白噪声得到了较好的抑制,但脉冲噪声仍然存在。采用中值滤波后的结果如图3(b)所示,从图中可以看出,中值滤波可以有效抑制脉冲噪声,但由其处理后的序列仍存在大量的白噪声分量。图3(c)为信号经中值-小波去噪方法去噪后的结果。按照笔者提出的方法,需在中值-小波去噪方法基础上,选择合适的窗口长度以及拟合多项式次数对其小波分解后的最后一层近似系数进行Savitzky-Golay滤波处理。通过调试分析,最后选择Savitzky-Golay滤波器窗口长度为7,多项式次数为4,因而卷积系数h=[0.021 6 -0.129 9 0.324 7 0.567 10.324 7 -0.129 9 0.021 6]。采用本方法去噪结果如图3(d)所示。从图3(c),(d)可知,中值-小波去噪法以及本方法均能较好抑制脉冲噪声和白噪声,但从图中不易看出哪一种方法更具优越性。为了进一步分析它们的去噪性能,对小波阈值去噪、中值-小波去噪以及本方法去噪过程中的最后一层近似系数进行提取,结果如图4所示。 图2 仿真信号波形Fig.2 The waveform of simulation signal 图3 各种方法对含噪信号去噪的效果图Fig.3 The comparison of various methods about noisy signal 图4 采用不同方法处理时的近似系数提取结果Fig.4 The extraction results of approximate coefficients in different methods 由图4可知,含噪信号先经中值滤波处理后再进行小波分解而得到的近似系数序列明显比直接小波分解得到的近似系数序列更加平滑,表明中值滤波可以有效抑制脉冲噪声,从而提高小波分解质量;而图4(c)与(b)相比,近似系数序列更加平滑,其形态特征更接近于原始信号,表明Savitzky-Golay滤波器能够有效平滑近似系数序列中的白噪声分量,同时保持了原始信号的细节特征。 为了进一步验证笔者所提方法整体去噪性能的优越性,表1为上述4种方法的去噪性能比较。可见,本研究去噪方法较其他3种方法各性能指标均得到了提升,表明本方法具有较好的去噪性能。 表1 各种方法对应的去噪效果评价指标 Tab.1 Evaluation indexes of de-noising effects corresponding to different methods 去噪方法RMSELCISNR/dBS小波阈值去噪法0.064 40.998 624.836 91.087 7中值滤波法0.040 40.999 428.896 61.936 0中值-小波去噪法0.029 20.999 731.707 30.984 5本研究方法0.025 00.999 833.062 10.970 4 为了验证所提方法在提纯水电机组摆度信号的有效性以及优越性,对某电站水轮发电机一号机组水导x轴方向的摆度信号进行提纯分析,机组转速为187.5 r/min,采样频率为1 kHz,采样2 000个点。实验整体结构如图5所示,传感器探头固定于水导机架处,如图5(a)所示,并通过光缆连接至实验箱,如图5(b)下方7个插孔,分别对应上导x,y方向、下导x,y方向、水导x,y方向以及下机架z方向。这里只需采集水导x轴方向的摆度信号。传感器采用电涡流位移传感器,系统硬件设计采用DSP技术,DSP采用TI公司的TMS320F2812芯片。 图5 实验平台 Fig.5 Experimental platform 图6为摆度实测信号波形。由图6可知,现场采集的信号存在大量的背景噪声,真实有效信号被淹没。从图6可以看出,信号中存在较强幅值的脉冲噪声。用不同方法对采集的信号进行处理。通过多次实验,最后选取滤波参数为:小波阈值去噪,db4小波基,分解层数为5层;中值滤波的窗口长度为17;中值-小波去噪,中值滤波器窗口长度为7,选择db4小波基,分解层数为3层;本方法中值滤波器窗口长度为7,选择db4小波基,分解层数为3层,Savitzky-Golay滤波器窗口长度为15,多项式次数为4,卷积系数为h=[0.046 4 -0.061 9 -0.063 6 -0.003 6 0.081 3 0.162 4 0.219 2 0.239 5 0.219 2 0.162 4 0.081 3 -0.003 6 -0.063 6 -0.061 9 0.046 4]。去噪结果如图7所示。 图6 摆度实测信号Fig.6 Real signal of throw 图7 各种方法对实测信号去噪结果Fig.7 Denoising results of various methods about real signals 图7(a),(b)为分别经中值滤波和小波阈值去噪后的结果。从图7(a),(b)可以看出,信号经中值滤波后,脉冲噪声得到了较好的抑制,但由其处理后的序列仍残留着平稳随机噪声,信号不够光滑;信号经小波阈值去噪后,白噪声得到大幅度的衰减,但因小波阈值去噪方法无法消除脉冲噪声的影响,使得消噪后的信号不够平滑。采用中值-小波去噪法以及本方法进行消噪后的信号分别如图7(c),(d)所示。比较图7中不同方法去噪结果可知,中值-小波去噪法以及本方法较中值滤波法、小波阈值去噪法有较大的改进,且采用本方法去噪后,信号中的白噪声以及较强脉冲噪声都得到了较好的抑制。 因为不能得到理想、无噪声的原始摆度信号,因而不能直接用前面介绍的均方根误差、局部相关指数、信噪比以及平滑度来衡量笔者所提方法在提纯水电机组摆度信号的性能。为了进一步验证本方法在提纯摆度信号的有效性以及优越性,计算时用实测摆度信号替代式(15)~(18)中的原始信号,且重新定义评价标准如下:若消噪后信号的RMSE值越大以及LCI值、SNR值、S值越小,则表明其更接近于原始信号,去噪效果越好[15]。采用不同方法对采集的信号进行滤波处理,分别计算去噪后信号的指标值。具体数据见表2。 表2 不同方法的去噪效果 从表2可以看出,本方法的4个指标均优于其他3种方法,表明所提方法具有较其他3种方法更好的去噪性能。 为验证所提方法对有效信号的保留能力,对实测摆度信号以及经上述不同方法处理后的信号进行FFT频谱分析,结果如图8(a)所示。从图8(a)可以看出,在低频段,去噪前后的频谱基本相同,即去噪后信号基本保持着原始信号的特征。从频谱特征来看,去噪后信号的能量主要分布在基频以及它的几个倍频中,跟理论分析基本一致。对图8(a)中基频所对应的区域A以及主要倍频区域进行放大,分别如图8(b),(c)所示。 图8 滤波前后信号频谱图Fig. 8 The signal spectrum of before and after filtering 如图8(b),比较滤波前后基频处对应的幅值可知,笔者提出的方法与原始信号对应的幅值最为接近,中值-小波去噪方法次之,中值滤波最差。表明笔者提出来的方法与原始信号重合度最高,即信号特征保留最为完整。从图8(a),(c)可以看出,在2~4倍频区,中值-小波方法以及笔者所提方法跟踪原始信号的能力较好,但从14 Hz对应的点开始,采用本方法去噪后的频谱曲线基本上处于采用中值-小波去噪后的频谱曲线的下方,特别是在15.6,20.8,27.6及30.7 Hz附近处,幅值明显小于采用中值-小波去噪后的频谱曲线所对应的幅值。这是因为Savitzky-Golay滤波器平滑了近似系数中的噪声分量,表明本方法对中频以及高频部分都有较强的衰减,有利于抑制噪声。分别观察采用小波阈值去噪、中值滤波后的频谱曲线。由此可知,单独采用小波阈值或中值滤波均不能有效跟踪原始信号,导致部分信号特征损失。采用小波阈值去噪后的频谱曲线到40 Hz时才有明显衰减,其有效去除了40 Hz以上的高频干扰,但未能消去16~40 Hz之间的中频干扰噪声。采用中值滤波方法去噪后的频谱曲线在高频处均有较高的幅值,这是因为中值滤波对高频白噪声抑制效果不佳,这与前面的理论分析一致。从上述分析可知,笔者提出的方法在有效保持原始信号细节特征的前提下更好地抑制了噪声干扰。 提出了一种中值-小波平滑综合分析方法。首先,对小波分析、中值滤波以及Savitzky-Golay滤波的原理以及去噪性能进行了分析,结合3种方法的性能特点,进行了组合滤波器设计。该组合滤波器不仅考虑了信号中的脉冲干扰以及小波分解后的细节系数的处理,同时采用Savitzky-Golay滤波器对小波分解后的近似系数进行了平滑处理。其次,通过仿真比较了4种方法去噪性能,对采用不同方法时小波分解后的近似系数进行了提取。仿真发现,采用中值-小波分解得到的近似系数再经Savitzky-Golay平滑处理后的新近似系数比其他方法得到的新近似系数更接近于原始信号特征。最后,将4种方法同时应用于稳定工况下水电机组摆度信号提纯。结果表明,所提方法在有效保持原始信号细节特征的前提下更好地抑制了噪声污染,验证了该方法在提纯机组摆度信号的有效性及优越性。
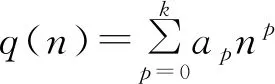

1.3 中值-小波平滑综合去噪方法
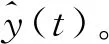
2 仿真验证

3 实验与分析


4 结束语
