基于偏随机秘钥遗传算法的舰船驻泊方案决策*

黄必佳，韦灼彬

（1.海军工程大学，武汉 430033；2.海军勤务学院，天津 300450）

0 引言

船舶调度问题主要涉及码头泊位的分配，即将到港船舶有序合理地安排到合适的泊位。在调度规划过程中，需要考虑诸如可用泊位数量、泊位长度、水深、船舶的吃水和长度、系泊时间和货物类型等［1］。而在军事范畴内，军港的舰船调度问题还要考虑舰船类型以及码头的服务保障条件，尤其是当接到舰船集结部署的保障任务时，制定驻泊方案将变得更加复杂。

国内外学者一直以来就泊位分配问题开展了积极有效的研究，文献［2］建立了基于排队论的船舶动态模型，从而对离散的泊位进行优化分配；文献［3-4］开发了启发式搜索算法作为泊位分配问题的一种新的多阶段搜索技术；文献［5-8］研究了集装箱港口的泊位分配问题，使用整数规划和遗传算法进行优化分配，以便快速服务于大型集装箱船舶。文献［9］针对公共泊位系统，采用了动态确定船舶泊位的方法，并将其与静态方法的结果进行比较。但目前的研究多以民用港口的泊位分配问题为研究对象，其理论研究成果并不能完全适用于军用港口的实际应用，单就军港泊位的分配问题而言，就与民用港口有所不同。在民用港口的情况下，泊位分配的目的是为了尽量减少靠泊费用支出，减少船舶靠泊或服务的总时长，增加泊位利用率。目前的研究也往往围绕最小化时间或等待时间等进行论述，通常情况下，民用船舶的移动仅发生在船舶完成装卸任务前后，并不需要移动泊位。

军港的主要任务是在港区内承担舰船下一步任务所需保障服务，在所有作战或训练任务完成后，舰船须返回母港接受补给以及其他保障服务，包括武器弹药、物资油料、应急维修等［10-11］。由于受港区泊位条件以及码头设施配备的限制，很可能无法一次性提供舰船所需的所有服务，因此，舰船往往会产生一次或多次移泊事件。为了尽可能减少因移泊所产生的时间延误，提高军港的保障服务效率，使得舰船尽快返回部署海域，本文构建了基于保障服务的混合整数规划模型（Service based Mixed Integer Programming，SMIP），使用一种遗传算法进行求解运算，所得结果与传统模型进行对比，并对影响目标结果的变量进行敏感性分析。

1 模型的数学描述

军港泊位分配的主要目标是为了能够有效分配泊位并满足舰船所需的多种保障需求，以便舰船在返回母港期间能够迅速得到补给，并在最短的时间内重新返回作战海域，即最大限度地减少在港口靠泊的舰船数量。通常也可以认为，这是一个使海上舰船部署数量最大化的问题。

1.1 模型假设

由于泊位分配问题较为复杂，涉及物理要素较多，因此，在构建SMIP 模型时需作出如下假设：

1）每个泊位都有足够的长度以允许所有舰船进行靠泊。

2）每个泊位的水深满足所有的舰船吃水深度。

3）每个泊位都能够提供最多靠泊3 艘舰船的电力电缆。

4）任意舰船不能在码头占用一个以上的泊位。

5）进行舾装改装的舰船单独靠泊。

6）舰长较短的舰船可以并靠在较长一方的外侧。

7）靠泊顺序从内部依次向外进行。

8）若舰船完成所有保障服务的时间先于预定出发日期，则舰船可以提前离开港口。

9）任意舰船不能同时接收多个服务。

10）将一天工作日分为上午和下午两个时间段，每天可以进行两次泊位移动。

1.2 模型建立

用舰船运转率表示处于海上部署状态下的舰船数量占舰船总数的百分比，模型通过尽可能地减少在港靠泊的舰船数量来最大化舰船运转率。最大化舰船运转率的相关参数、变量和数学模型如下所示：

对上述模型进行说明：

常量变量。SAia表示舰船i 的参数信息（power表示舰船需要的接岸电缆数量；ft 表示抵达日期；lt表示出发日期）；PAja表示泊位j 的参数信息（power表示码头所能提供的电缆数量；capactiy 表示码头的容量）；SQTis表示舰船i 需要保障服务s 的时间；NONEST 表示需要单独系泊的舰船集合；MP 表示进行舾装改装的泊位；P（s）表示可以提供保障服务s 的码头集合；SQis，若舰船i 需要保障服务s，则SQis=1，否则SQis=0；PQjs，若泊位j 可以提供保障服务s，则PQjs=1，否则PQjs=0。

决策变量。Yijk，若舰船i 在k 时被安排到泊位j，则Yijk=1，否则Yijk=0；Zis，若舰船i 没有接受到保障服务s，则Zis=1，否则Zis=0；Mijk，若在k 时，舰船i 在泊位j 发生移泊事件，则Mijk=1，否则Mijk=0。

目标函数表示通过最小化靠泊舰船的数量，来实现最大化舰船的运转率；式（1）保证了任意舰船只能停在一个泊位上；式（2）保证了任意码头在任意时段最多并靠停泊3 艘舰船；式（3）对舰船的在港时间进行了约束；式（4）保证了在规定时间范围内不得中途离港；式（5）保证了若舰船所需要的保障服务均已完成，则可以提前离港；式（6）保证了在计划时间以外不得在港内驻泊；式（7）对Zis进行了定义；式（8）保证了舰船所需要的保障服务只能从可提供该类保障服务的泊位上获取；式（9）对移泊事件进行了表达，假设舰船1 在k=1 时处于泊位1，并 在k=2 时 转 移 到 泊 位3，当 且 仅 当Y1，1，2=0，Y1，1，1=1，Y1，3，2=1，Y1，3，1=0 时才能满足下列不等式：

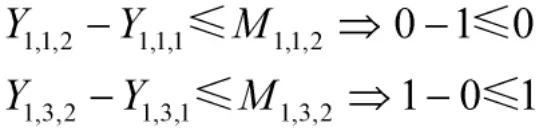
式（10）保证了第j 个码头必须有足够的电缆数量满足分配到其进行保障舰艇的需求；式（11）对码头的容量进行了约束；式（12）保证了舰船i 在k 时被安排到泊位j 接受保障服务s，若服务时间超过2个工作日，则舰船在保障服务完成之前不允许进行泊位移动；式（13）保证了需要舾装改装的舰船只在支持该保障服务的泊位上单独靠泊；式（14）～式（16）对决策变量进行了约束。

2 SMIP 模型的算法设计及应用

遗传算法（Genetic Algorithm，GA）是生物启发式算法，为优化问题提供最优或近似最优解［12-13］，大量的相关研究已证明GA 可有效地应用于数学规划的实际问题当中。近年来，偏随机密钥遗传算法（Biased Random Keys Genetic Algorithms，BRKGA）已成为解决NP-hard 问题的新途径，并得到广泛关注［14-15］。BRKGA 能有效避免一般GA 的典型缺陷，提高收敛速率，并快速形成高质量的可行解，在编码形式上明显优于其他改进算法，并已得到有效验证［16-17］。

2.1 BRKGA 在SMIP 模型的设计分析

将BRKGA 应用到SMIP 模型的优化求解中，本文按照如下步骤进行设计计算：

1）染色体编码。本文根据泊位分配以及SMIP模型特点，在［0，1）中以实数生成的随机数进行编码，再对等位基因按升序排序调整。

2）初始化种群。依据编码规则给出种群的初始解，每一个都是随机生成的，并且满足问题所施加的可行性标准。

3）适应度排序。通过目标函数，计算个体适应度值并排序。

4）对种群进行复制、交叉、变异操作。为了单调提高启发式算法的寻优速度，从优质解中按一定比例复制到下一代，这种策略被称为精英策略，其主要优势在于可使最好的解决方案在每一代中保留并继承；在BRKGA 中，交叉过程则是将种群分成两个亚群，即精英阶层和非精英阶层。精英分子群体包含一小组种群的最佳解决方案。其余的解决方案属于非精英人群。为了产生后代，BRKGA 从精英分群中选择一个父代，从其余的种群中选择另一个父代；在BRKGA 中，变异的使用范围比一般GA 更加广泛，通过引入变异算子，将生成的新个体加入到下一代，这些新个体是从与原始种群相同的分布中随机生成的，从而起到防止种群过早收敛到局部最小值的作用。一个交叉操作算例以及新种群产生操作如图1、图2 所示。

图1 交叉操作算例

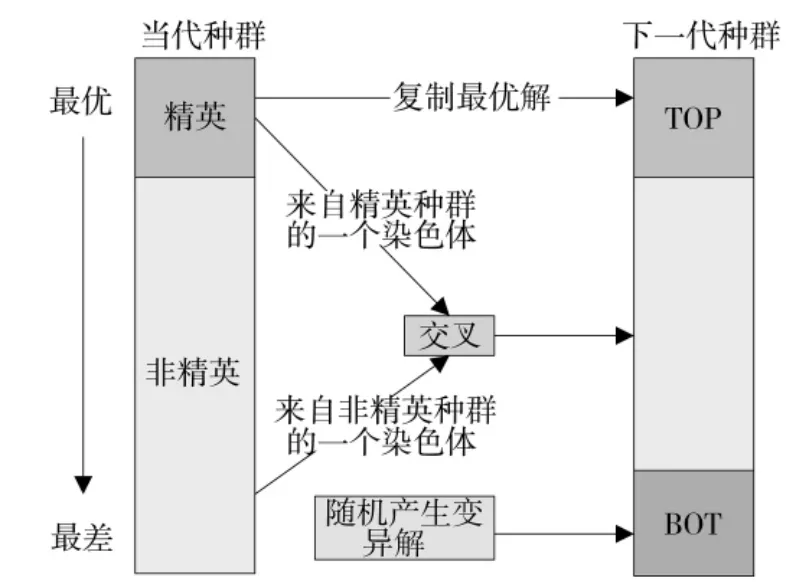
图2 新种群形成操作

5）判别新种群是否满足终止条件。如果已经存在一定数量的连续迭代而没有改善群体中最优的个体或已达到某代的总数，则停止运算，输出优化结果；若不符合条件则重新返回步骤3）、步骤4）。

2.2 算例想定及参数设定

为测试SMIP 模型的有效性，本文设置了想定的应用场景，采用15 艘舰船、4 座码头、10 d 规划期进行分析。

军港泊位提供的保障服务可分为6 类：应急维修、油料补给、弹药装填、起重机械、抗腐蚀涂装、舾装或改装。表1 对各舰船的参数特性进行了说明；表2 给出了每艘舰船需要的保障服务和服务时长。

表1 舰船特征数据

表2 舰船的保障服务需求及时间

假设某舰船在海上执行任务时消耗了8 枚制导导弹，40%的燃油，经受了5 d 的海水腐蚀以及1台发电机发生故障。当进入港内接收这些保障服务时，决策人员可以通过使用历史数据的记录来估计加载保障服务的时间，并且可以将此类数据用于泊位分配。

表3 给出了码头的相关参数，所有的码头可以最多同时容纳3 艘舰船，但是一个支持舾装改装的码头仅限于1 艘舰船；表4 给出了码头可提供的保障服务，1 表示可提供，0 表示不提供。

表3 码头特征数据

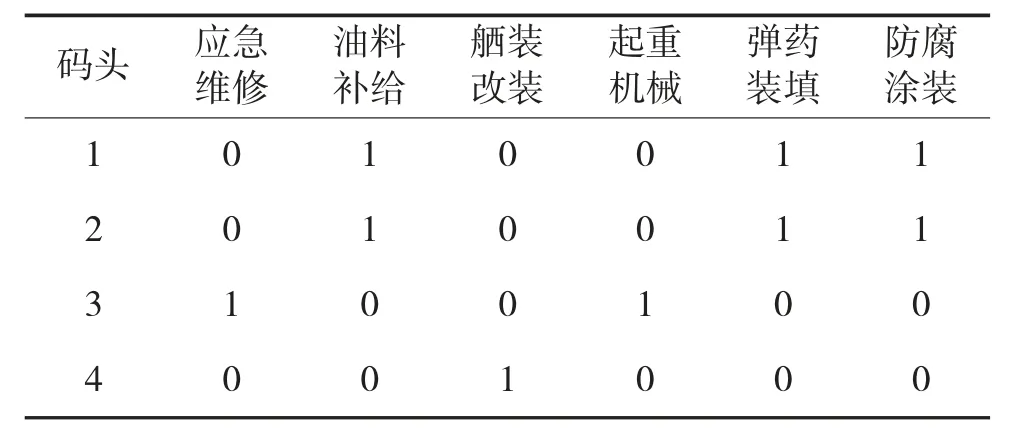
表4 码头可提供的保障服务类型

3 泊位分配结果及分析

BRKGA 的基本参数设置：使用种群规模为100，精英率为0.1，变异率为0.1，交叉概率为0.75，运行平台采用Inter Core i5，CPU 3 230 M 2.60 GHz，RAM 8 G。图3 显示了k=1 时，码头泊位的分配结果。算法的迭代效果以及计算结果如图4 所示。

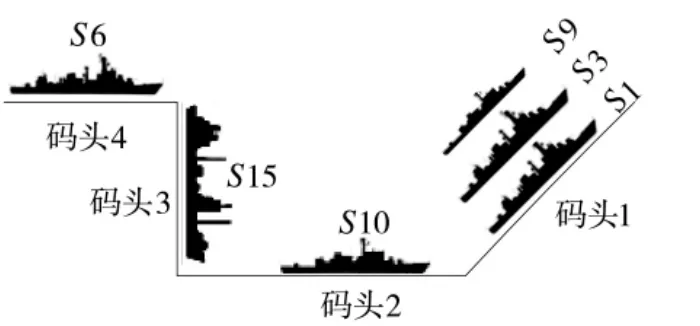
图3 码头泊位分配示意图

图4 BRKGA 的计算结果

同时，为了验证SMIP 模型在泊位分配上的可行性，本文将SMIP 模型得到的方案与现有的舰船调度方法进行对比，该方法的泊位分配按照以下原则完成：

1）确定舰船所需的保障服务数量；

2）检查码头的泊位数量。如果没有可用泊位，则先将其分配给一个临时泊位，但要尽量减少等待时间。

3）分配泊位，使舰船能够在最短的时间内得到必要的服务，尽量减少不必要的泊位移动。

对上述原则用MIP 的相同格式构建模型，表5和下页表6 分别表示两种泊位分配方法的结果，两种结果均显示了在规划时间内舰船所在码头的相对位置，以及接受到的保障服务类型。

通过对比两种泊位分配方案，可以明显反映两种模型的性能。例如，在SMIP 模型中，k=3 时进入码头4 的舰船S12 的保障服务流程按照W→R→O→F 的顺序，并且在此期间发生两次泊位运动，且不存在非必要的移泊运动。

而在表6 的结果中，S12 出现了不必要的泊位移动。在k=3 时进入码头1 的舰船S12 的保障流程按照O→R→F→H→W 的顺序进行，在此期间进行了3 次泊位移动，其中一个泊位移动是非必要的。O和F 可以在同一个码头进行，但在O 之后，却移动了泊位来接受服务R，发生了非必要的移动，在这之后还出现了一个时间段的等待过程，从上述结果可以看出，使用现有的调度模型所产生的结果，在一定程度上增加了舰船的在港时间，从舰船运转率来看，也不如SMIP 模型的优化效果。

表5 SMIP 模型的泊位分配结果

本文所使用的SMIP 模型是基于舰船运转率最大化并满足所有舰船的保障服务需求而构建的，而现有的调度模型中的舰船S14 并没有得到W 的保障服务。另一方面，根据SMIP 模型的计算，其目标函数值为97，海上作业的舰船数量为10.15，舰船运转效率为67.6%，而现有模型分别为106 和9.7，舰船运转效率为64.6 %，这就意味着本文所使用的SMIP 模型可以进一步增加海上部署的舰船数量。

表6 现有调度模型的泊位分配结果

使用SMIP 模型进行规划，整个调度系统共计发生19 次移泊，现有的调度模型发生21 次移泊。而在实际的调度规划中，应尽量减少泊位移动，因为泊位移动不仅会导致整个工作时间的延迟，而且会增加人员、设备、油料等资源的成本，这也充分体现了SMIP 模型在节约保障资源上的能力效果。

在SMIP 模型中，保障服务的数量和服务的持续时间取决于舰船实际的损伤程度和军事物资的缺乏度，因此，具有不确定性，所以这种不确定性可以通过对变量的敏感性分析来反馈。

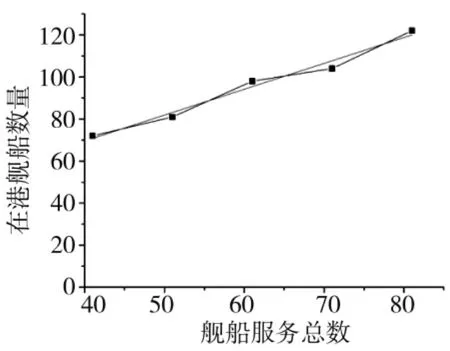
图5 目标函数随舰船服务总数的变化曲线

首先，是保障服务数量的变化。例如，如果舰船在任务后未产生损坏，则不需要应急维修，所以保障服务数量不会增加。图5 显示了模型的分析结果。随着服务总数每增加10 个单位，港内舰船呈现线性增加的趋势（斜率为1.23）。这也说明了军港需要在码头配套设施改造升级上进行系统规划，提高单一码头的多元化保障能力，才能更有效地满足舰船日益增长的保障服务需求。

其次，是服务总时长的变化。例如，如果舰船的武器消耗量增加，则也意味着增加武器装载的时间。图6 显示了模型的分析结果。随着服务总时长每增加15 个单位，在港舰船数量也将呈现线性增加的趋势（斜率为1.09）。这也说明了军港需进一步提升专业化保障服务水平，提升保障效率。

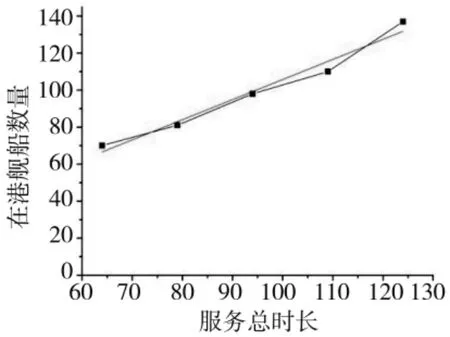
图6 目标函数随保障服务总时长的变化曲线

4 结论

为了获得必要的保障资源，舰船必须在最短的时间内在军港完成必要的保障服务，本文构建了基于保障服务的泊位分配模型，采用BRKGA 对模型进行应用设计，并结合军事背景构建了一个想定算例，通过BRKGA 的优化计算，所得到的泊位分配结果满足所有舰船的服务保障需求，同时与现有的舰船调度方法进行对比分析，结果表明，本文构建的SMIP 模型可以提高舰船运转率，具有较高的可行性和实际应用价值。未来的研究方向将综合考虑泊位成本、港口拖船、燃料成本、港点劳动力成本等因素，并将成本因素纳入泊位分配问题，这将有助于降低整体调度系统的运营成本。另外，考虑战时舰船的损伤程度，以及保障优先级，也将成为泊位分配的重要因素。