符号网络下平衡结构对舆论形成的影响

张奥博,樊 瑛,狄增如

(北京师范大学系统科学学院，北京 100875)

0 引言

符号网络早已是社会网络研究的重要领域。在20世纪40年代，Heider[1]应用社会心理学领域的研究结果，提出了一种用三角形来描述以人为研究主体的关系中积极作用和消极作用方法。与之相关的基础性理论有两个：地位理论和结构平衡理论[6]。结构平衡理论是由社会学家Heider[1]提出的，结构平衡理论认为图1中，a和b是平衡结构，c和d是非平衡结构。之后Davis[8]提出了弱平衡理论，认为三边均为负号也属于平衡结构。Cartwright[9]等人则基于结构平衡理论从图的角度重新对其刻画。Ernesto[10]和Alec[11]利用矩阵的秩计算符号网络中的平衡性，通过对不同长度的环按权重求和来进行计算。符号网络还被广泛应用于链路预测、符号预测和社团划分中，Traag[12]等人对Q函数加入符号，以对符号网络进行社团划分，Larusso[13]提出用模拟退火算法最大化社团内的正边和社团间的负边来得到结果。Agrawl[14]基于矩阵分解提出了符号网络的链路预测的方法，Liu[15],Chiang[16]等人提出了对于符号网络中未知边的符号预测的方法。在Szell等人[17]的研究中，通过实证分析证实了平衡结构的比例是随着时间演化而逐渐增长的，揭示了社会网络的结构演化性质。Wu[18]等人探索结果与动态演化的关系，揭示了负边对极化观点的影响，Pan[19]等人提供了一种分布式数据驱动的防范验证大规模符号网络的结构平衡。

图1 结构平衡理论中的三角形结构Fig.1 Triangle structures in structural balanced theory

符号网络研究主要集中在理论探究、社区检验、社团划分等网络结构分析和动力学演化分析等,但总体来说，在符号网络动力学的研究中，对于网络上信息扩散、合作演化、网络舆论形成等问题的相关研究还较少。

舆论形成是网络动力学研究的重要主题。舆论是社会公众对于某一观点或事件所持意见的集合，社会舆论对于社会的发展和进步起到了关键性的作用，舆论的形成与传播是社会复杂系统研究中的重要问题。特别是在信息技术飞速发展的今天，人与人之间的联系和影响越来越紧密，社会系统的复杂性日益凸显，基于复杂网络方法研究舆论的动态演化、形成规律及传播特点，具有重要的理论意义和现实意义。

本文将着重研究符号网络上的舆论形成，探索符号网络中的平衡结构对舆论形成的作用。基于Ising模型、多数投票模型的相关研究主要关心系统的统计性质和相变行为，在本文中，我们利用离散动力学模型，更加关注舆论形成的时间演化行为，关注平衡结构性质对系统演化过程和最终稳恒状态的影响。

1 模型构建

本节主要建立符号网络上舆论形成的动态演化模型，包括基于投票模型的顶点状态演化以及状态与结构的耦合演化。我们将首先讨论N=20*20的二维三角形晶格网络如图2(周期边界条件)，其中圆形为正节点、三角形为负节点，粗线为正边、细线为负边，在第3节中把模型推广到ER随机网。

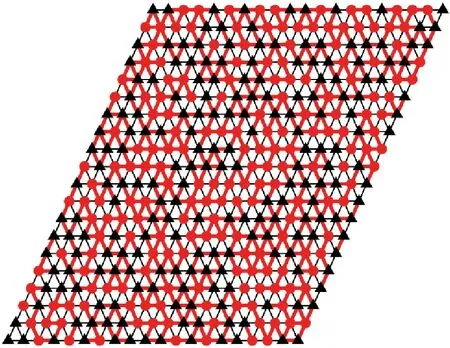
图2 初始符号网络图Fig.2 Initial signed network diagram

1.1 节点状态演化规则

考虑网络中的顶点(个体)i，它有两种态度可以选择，用自旋Si来表示它对某问题的具体态度，自旋向上(Si=+1)代表支持，自旋向下(Si=-1)代表反对；节点之间的连边Aij代表个体之间的关系，+1代表积极关系，倾向于使两个体的态度相同，-1代表两节点间的关系为消极关系，倾向于使两个体的态度相反，演化过程个体态度通过符号网络受到与其有联系的其他个体观点的影响，我们假设个体i态度演化动力学为：

(1)

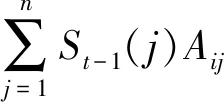
依据多数投票模型，网络中每个个体的态度由上一步中邻居节点态度的大多数来决定，大多数人的态度选择对个体影响程度由pc决定。在本文中，我们暂不考虑节点状态随机取值的情形取pc=1，完全由多数规则决定个体状态演化。

1.2 连边演化规则

在模型中，我们将同时在演化过程中考虑个体关系的改变，两节点间连边的正负号会在一定程度上由两节点的态度所决定，建立其动力学演化机制如下：

(2)

如果两个相邻个体态度相反，则在一定程度上可认为两者的关系也存在负向作用，态度相同则认为关系为正向，所以给出动态演化中连边的演化规则，连边的状态有一定概率由其连接两节点的状态给定，否则不改变连边状态。其中，pc′为连边按连接两节点状态改变的概率。将连边演化规则与节点状态演化规则相结合更能体现真实状况，态度观点的改变也可能会引起个体间关系的变化，关系的改变也会作用到个体的态度演化。

2 演化模拟与结果

2.1 负边比例与平衡结构比例的关系

根据图1中4种三角形结构计算平衡结构比例，对于任意3个节点i,j,k，设它们之间的连边的值分别为Aij、Aik、Ajk，则其结构性质由式(3)决定：

(3)

因此，给定符号网络中负边的比例p，则(1-p)3为图1中(1)所占比例，3*p2(1-p)为图1中(2)所占比例。忽略三角形之间的相关性可知晶格网络中平衡结构比例与负边比例p的函数关系为：

f=(1-p)3+3*p2(1-p)

(4)

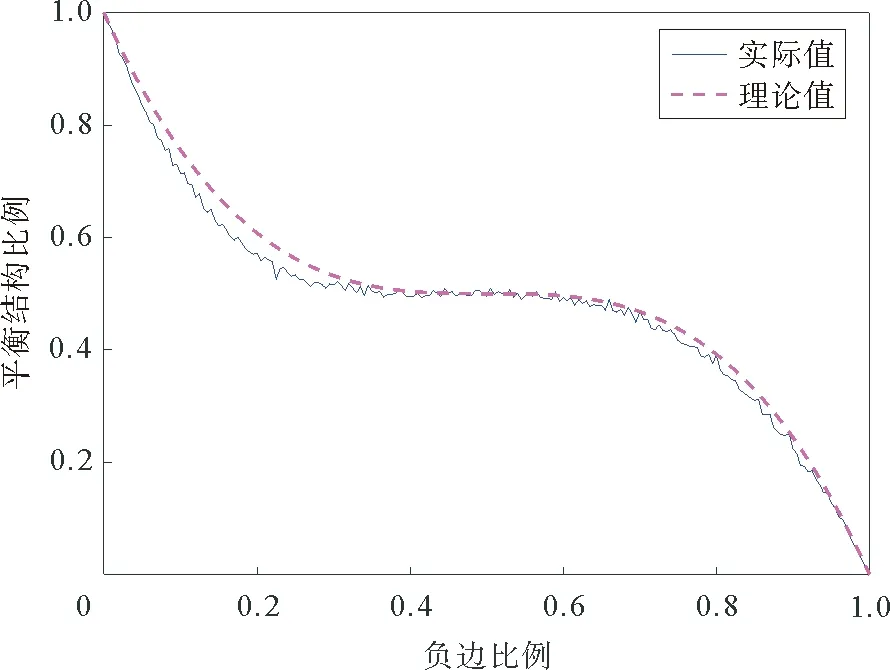
图3 负边比例与平衡结构比例关系图Fig.3 The relationship between ratio of negative edges and ratio of balanced structures

从0到1以间隔0.005给定负边比例，随机生成一组符号网络计算平衡结构比例，得到负边比例与平衡结构比例的模拟结果，并与理论值进行对比。如图3，横坐标为符号网络中的负边比例，纵坐标为该负边比例下平衡结构的比例，实线为模拟结果，虚线为根据公式(4)计算得出的理论值，能够较好进行拟合。

2.2 节点状态演化模型

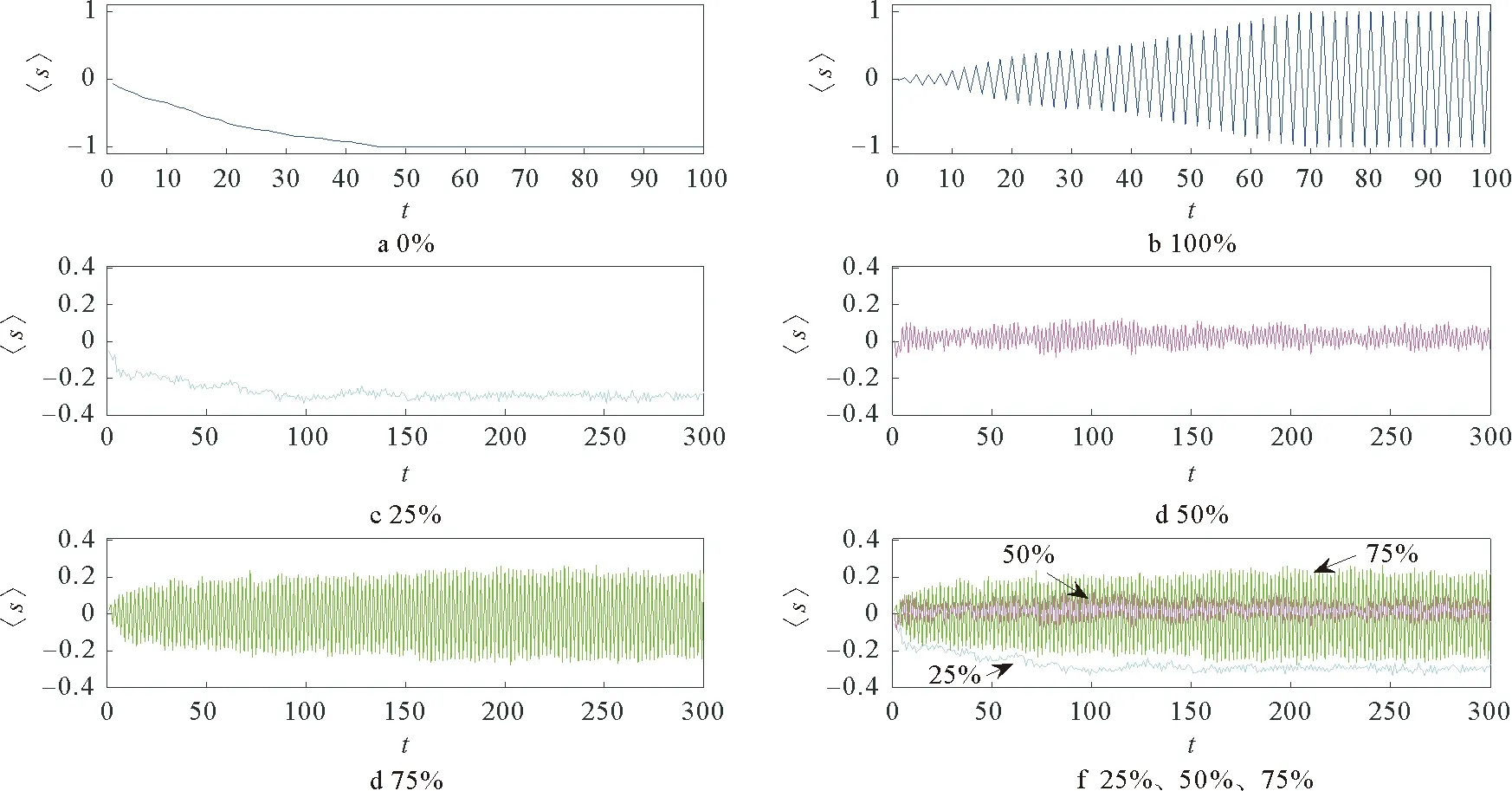
图4 不同负边比例下节点状态平均值〈S〉变化图Fig.4 The change diagram of 〈S〉 under different ratios of negative edges

当负边比例为0时，符号网络中点的状态由随机分布逐渐演化为分为正负两个区域，平均演化到50步后平均值〈S〉及所有节点均达到稳定状态，最终状态为点均为正或点均为负，也有可能会出现正负节点分为两个区域的现象。在负边比例为100%时，平均演化到100步左右时平均值〈S〉及所有节点均呈二倍周期状态，如图4b，最终状态为点均为正或均为负或分为两个区域波动。

当负边比例介于0～100%之间时，呈现一种伪随机状态，整体波动无趋势，部分节点呈二倍周期的变化。分别对负边比例为25%、50%、75%的情况进行模拟，结果如图4c、d、e所示，将3个结果进行对比(见图4f)，可以发现随着负边比例的增加，〈S〉波动的平均值会越来越趋向于0，波动的幅度也会增加。从微观角度来看，存在部分节点呈二倍周期波动，将二倍周期变化的节点提取出来如图5，发现负边比例越大，二倍周期变化节点越多，越容易出现节点分区变化的现象。

本文认为这种波动规律与网络中的平衡结构比例有重要的关系，因此计算了在不同平衡结构比例下波动最大幅值与波动的平均值，所有比例下的演化在300步后都趋于一个相对稳定的状态，因此计算每次演化300-800步的波动的平均值以及最大幅值(波动最大值)，取多次结果进行平均结果如图6所示，随着平衡结构比例的增加，波动的平均值越趋近于0，最大幅值呈下降趋势，说明了符号网络的平衡性对波动性的影响。

图5 25%、50%、75%负边比例周期变化节点结构图Fig.5 The period changing nodes’ diagram under different ratios of negative edges

在节点状态演化模型中，平衡结构比例对符号网络演化的波动性有着重要的作用，比例越低，越易使网络产生二倍周期波动的现象，越易形成观点一致且保持相同周期变化的小集团，波动的最大幅值越大，平均值越小。

2.3 节点状态与连边耦合演化结果

节点与连边耦合演化模型中，在对点进行演化的基础上，加入对边的演化规则(5)，进行演化。在0、25%、50%、75%、100%五种比例的符号网络下观察演化的过程及结果。同时在边按概率的演化规则基础上，使边在不同的时间尺度下进行演化，观察结果。

(5)

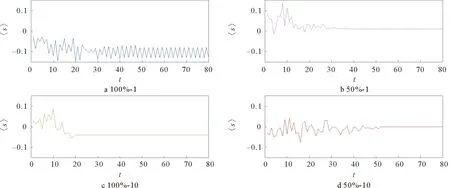
图7 耦合模型下符号网络〈S〉演化结果Fig.7 The results of 〈S〉 under coupled model

当边每一时间步变化一次且按照pc′=100%进行演化时，会在演化至60步左右时，平均值〈S〉和部分节点会呈现二倍周期的波动状态，如图7a所示，pc′=50%进行演化时，平均值〈S〉和所有节点会呈现稳定状态，如图7b所示。 由于现实生活中关系变化的时间尺度一般会长于态度的变化，所以改变时间尺度使边每10个时间步变化一次，时，pc′=100%演化至20步左右，〈S〉和所有的节点都会呈现稳定的状态，如图7c所示，pc′=50%时，演化至50步左右，平均值〈S〉和所有的节点都会呈现稳定的状态，如图7d所示。发现降低连边演化的概率会延长系统达到稳态的时间，在连边演化的规则下，符号网络的平衡性会随连边的演化而逐渐提高，图8为pc′=50%，时间尺度为10时平衡结构比例的演化情况，发现随着演化的进行系统的平衡性增强。

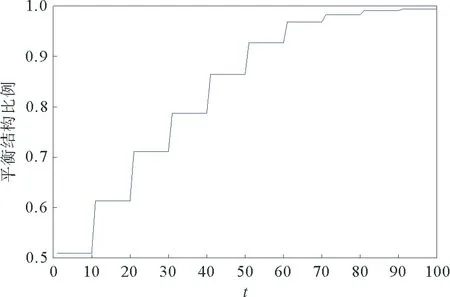
图8 耦合模型下平衡结构比例的变化趋势图Fig.8 Trend diagram of the proportion of the balanced structures under the coupled model

当连边演化的时间尺度为10时，在关注演化过程中的微观结构时可以发现，在10个时间步以内负边比例为0%或100%时会明显区分出两个状态相反的集团，但是当在连边进行演化之后不会产生节点状态全部趋同的情况，而是分成集团，集团内的节点状态均稳定且相同。

综上所述，节点与连边耦合演化时，边的演化概率pc′=100%，平均值〈S〉和部分节点会呈现二倍周期的波动状态，当改变演化概率pc′和边变化的时间尺度时，平均值〈S〉和所有的节点都会呈现稳定的状态，初始平衡结构比例对演化结果无明显影响，演化过程中平衡结构比例不断增加。

3 随机网络与完全平衡随机网络对比结果

根据连边的演化规则，边的演化概率pc′=100%，只需对连边进行一步演化，就可以构成一个完全平衡的网络结构。为研究网络平衡性对舆论形成的影响，分别生成随机符号网络和完全平衡的随机网络，对节点赋予相同的初始状态并进行演化。分别生成负边比例为10%、20%、30%、40%、50%的随机符号网络和完全平衡网络，按照节点状态演化规则进行演化。

(6)

观察演化结果，发现在平衡网络下，上述负边比例的符号网络中节点的平均状态〈S〉和所有节点的状态最后均能达到稳定的状态，如图9a所示，对每一比例分别进行10次计算，得到其达到平衡的平均演化步数为6.06步且在不同比例间没有显著差异；但是随机网络平均状态会呈波动状态如图9b所示，平均在200步左右会出现围绕一个均值波动的情况。

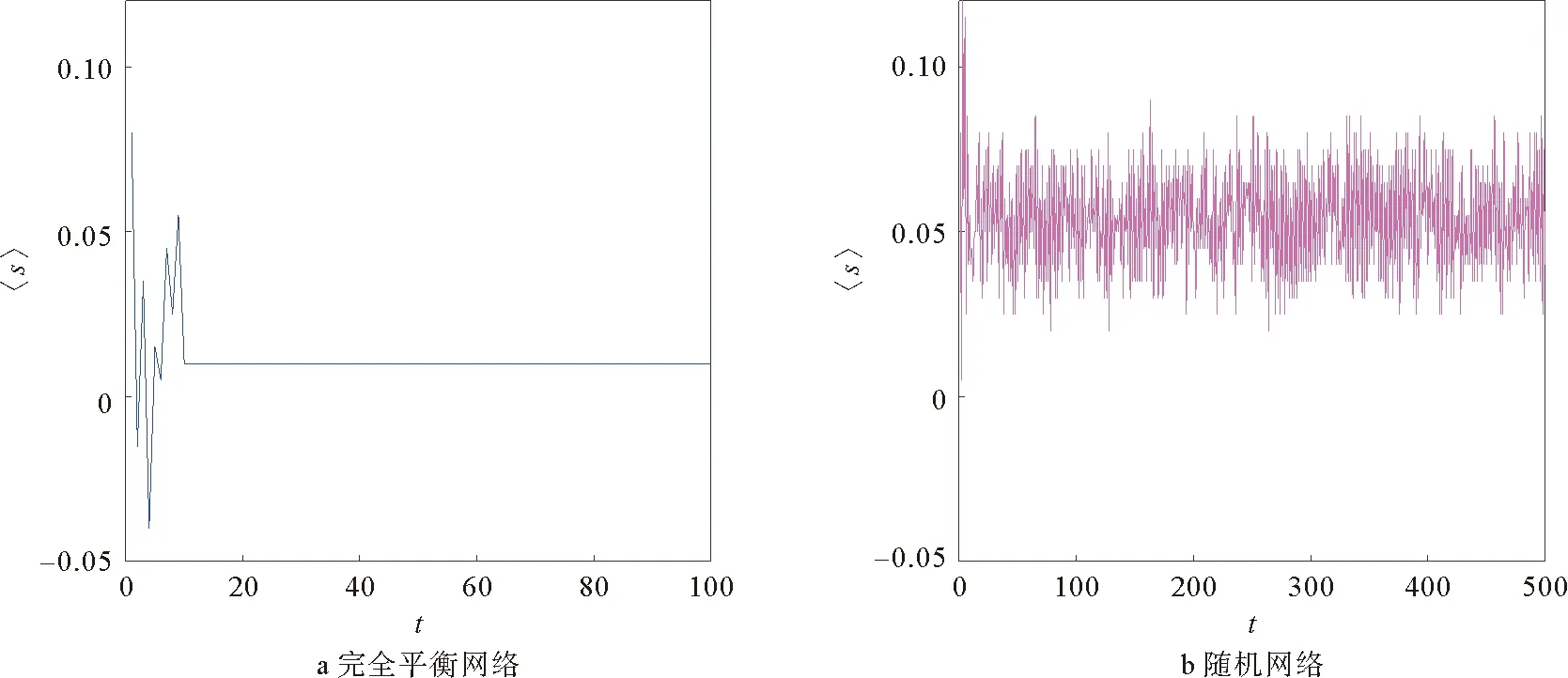
图9 完全平衡网与随机符号网〈S〉值对比Fig.9 Comparison of 〈S〉 between fully balanced network and random symbol network

在演化过程中，记录所有节点的演化，根据节点的状态分为正节点和负节点两个社团，并用邻接矩阵表示，将状态为正的节点置于前一部分，状态为负的节点置于后一部分，再对边的邻接矩阵进行变换，并且随演化进行，社团内节点是变化的，邻接矩阵随演化调整，得到每一时间步下变换后的邻接矩阵，并将正边标记为圆形，负边标记为三角形，如图10所示。发现在平衡网络下，随着演化的进行，最终会形成社团内的连接均为正，社团间连接为负的两个社团。

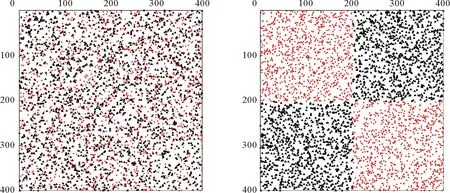
图10 完全平衡网连边矩阵演化过程图Fig.10 the evolution diagrams of completely balanced network’s Adjacency matrix

4 结论

计算在不同负边比例下的三角形平衡结构，得到平衡结构比例随负边比例的变化曲线，发现能很好地通过给定负边比例计算平衡结构比例理论值；在对节点状态的演化模型中发现，负边比例会影响网络平衡性，进而影响系统稳定状态的群体一致性，非平衡结构比例越高序参量越靠近0点，越易产生周期变化，在负边比例为0%时会出现状态趋同的现象，比例为100%时，全部节点均呈二倍周期变化；可以观察到整体演化结果存在着趋于系统舆论平衡和周期变化情形，可以发现，产生周期变化的构型由非局域平衡结构以及顶点状态共同决定；边与状态的耦合演化，特别是考虑相互作用调整与状态演化的时间尺度差别时，会增加系统演化的复杂性，系统会具有更丰富的稳态演化模式，连边调整的概率和时间尺度的引入会影响耦合演化的周期变化；完全平衡网络能加速系统舆论趋于稳定状态，并且有利于区分符号网络中的正负节点，将其分为两个社团。