基于社交网络结构特征的S2IR谣言传播模型

瞿倩倩，韩 华，吕亚楠，贾承丰，马媛媛

(武汉理工大学理学院，武汉 430070)

0 引言

谣言传播作为一种社会传染过程[4]与疾病传播非常相似，因此谣言传播的研究大都基于流行病传播模型[5]。Daley 和Kenal提出了经典的DK谣言传播模型[6]，它是把个体分成3类：无知者、传播者和免疫者。无知者是不知道谣言的人，传播者是散布谣言的人，免疫者是知道谣言但不传播谣言的人。Maki和Thompson延伸了DK模型，假设当传播者与另一个传播者接触时只有最初的传播者会变成免疫者[7]。在此之后，学者们开始在这两种传统模型的基础上进一步研究谣言传播。随着复杂网络理论的发展，由一些节点相互连接组成的复杂网络可以更合理地描述现实的复杂系统，因此越来越多的学者开始研究网络谣言传播过程。Zan Yongli[8]考虑网络中存在多种谣言传播的情形，假定两种谣言开始传播的时间不同且谣言内容无关联，引入选择参数来表示两种谣言的吸引力，建立了两种谣言传播模型：DSIR模型和CDSIR模型。Zhang Yaming等[9]提出一种考虑超扩散机制的新的谣言与权威信息传播模型，运用平均场方程推导基本再生数与最终传播规模，并在BA无标度网络与新浪微博网络上进行仿真分析。Qian Zhen等[10]基于SIR模型建立了一种复杂网络上具有独立传播者(independent spreader)的谣言传播模型，发现独立传播者的引入对谣言传播过程与稳态均有影响，突破了传统的必须通过连边传播的方式，认为无连边也能传播。Huo Liang’an等[11]建立了同质网络上的谣言传播模型, 考虑非线性传播率并将传统模型中谣言传播者进一步分为活跃与不活跃两类状态, 计算基本再生矩阵的特征值得出基本再生数。

谣言传播依附于具体的网络，网络结构必定会对谣言传播过程产生影响，然而上述研究没有充分考虑网络结构特征对谣言传播率的影响，因此，本文基于网络结构特征引入谣言信度函数以及个体亲密度函数的概念，定义一种考虑网络结构特征的非一致传播率。同时，考虑谣言传播者本身的信谣程度可能不同，以至于传播谣言的力度有所差异，在经典DK模型[6]的基础上将谣言传播者进一步分为完全信谣者与轻度信谣者两类。由于现实社交网络中存在用户注册与注销的情况，考虑网络中节点的移入与移除，依据平均场理论建立一种具有非一致传播率的S2IR网络谣言传播模型。本文第1节通过建立的社交网络谣言传播模型得出谣言传播的微分动力学方程；第2节推导出谣言传播模型基本再生数的表达式；第3节对随机免疫与目标免疫两种免疫策略进行分析对比；第4节仿真分析谣言传播的特点，探究模型中的参数对传播过程的影响以及几种免疫策略的效果，在仿真网络与实际网络上验证模型的有效性；第5节针对社交网络谣言传播得出结论。

1 具有非一致传播率的S2IR谣言传播模型

借助复杂网络的相关概念，将社交网络中的用户抽象为复杂网络中的节点，用户间的好友关系抽象为节点之间的连边。在经典DK谣言传播模型基础上，考虑传播谣言的用户的信谣程度不同导致传播谣言的力度存在较大差异，把网络中的节点分为五类：从未听说过谣言的无知节点S、完全信谣节点I1(传播谣言的力度较大)、轻度信谣节点I2(传播谣言的力度较小)、曾经听说过谣言但不会再相信谣言并且不会再传播谣言的免疫节点R以及空节点。现有的谣言传播模型大都将所有节点的谣言传播率视为同一常数，而实际网络中的谣言传播率并非都相同。鉴于此，本文利用网络结构特征定义谣言信度函数与节点亲密度函数，提出一种新的非一致传播率。

1.1 谣言信度函数

以往的谣言传播模型往往忽略节点之间的差异，假定节点的抗感染能力一致。事实上，节点度的大小会影响节点的抗感染能力。一方面，在实际的社交网络中，度大的节点一般是网络中比较重要的节点，这样的重要节点往往是较早加入网络中的，它们具有更多的经验与更强的防范意识，相应的抵抗谣言的能力也就更强，因此它们接收谣言后听信谣言且成为谣言传播者的概率也就相应降低了[14]。另一方面，节点的度越大，它可以选择进行交流的邻居节点数越多，每个节点的时间、精力有限，度越大的节点在与传播谣言的邻居节点进行接触时相信谣言的可能性就越小[15]。所以，尽管度大的节点与谣言传播者接触的机会更多，但由于自身具有较强的抗谣言的能力，其每次接触谣言时相信谣言的概率反而会低于网络的平均接触传染率[14]。针对以上分析，引入谣言信度函数α(k)来表示度为k的节点对谣言的听信程度(0≤α(k)≤1)，α(k)随着节点度k的增大而减小。

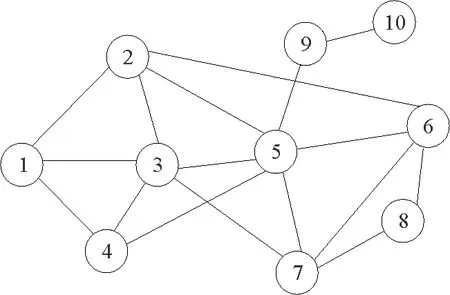
图1 网络拓扑示例图Fig.1 An example network topology diagram

1.2 节点亲密度函数

谣言传播所依附的网络的结构对传播过程具有重要影响，为研究网络结构特征对谣言传播概率的影响，采用节点相似性来定义节点亲密度函数。为描述方便，以图1所示案例来定义传播模型的网络拓扑结构。令g表示网络中的一个节点，取值为网络节点编号，下面定义网络节点的相关参数。

定义1节点的度k(g)。即节点g的邻居个数，如k(1)=3。

定义2节点的邻居集合Γ(g)。即节点g的所有邻居节点的集合。如Γ(1)={2,3,4}。

表1 邻居节点集合、邻居节点度、共同邻居数及节点亲密度Tab.1 Neighbor node set, neighbor node degree, number of common neighbors and node intimacy

1.3 新的S2IR谣言传播模型

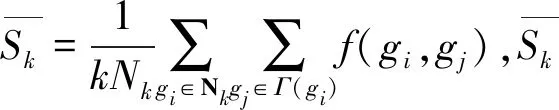
(1)

(2)

其中β为强化参数。式(1)中，当β=0(只考虑节点信度)时，式(1)等价于文献[14]中SIR模型的传播率，它能反映节点的差异性。

对于建立模型所需要的一些假设和参数描述如下：

1) 谣言传播初始，选取一定比例的节点分别作为初始传播节点I1、I2；

2) 在t时刻，任意一个度为k的谣言无知节点S被其传播谣言的邻居节点I1感染的概率为λ1(k)、被传播谣言的邻居节点I2感染的概率为λ2(k)，被感染后的节点以概率τ1变成节点I1、以概率τ2变成节点I2；

3) 受辟谣工作的影响，传播节点I1会以概率γ1变成免疫节点R，传播节点I2会以概率γ2变成免疫节点R(γ1<γ2)；

4) 传播力度较大的完全信谣节点I1由于逐渐对谣言失去兴趣或遗忘等原因会以概率η变成传播力度较小的节点I2；

5) 空节点变成S节点的概率记为注册率b，所有节点变成空节点的概率记为注销率μ；

6) 在t+1时刻，由于个体所处状态会随时间而变化，谣言无知节点S会再次与其传播谣言的邻居进行接触，传播过程会跳转至第2)步。

图2 S2IR模型节点状态转移图Fig.2 The state transition of S2IR rumor spreading model

谣言传播机理如图2所示。利用平均场理论[17]，由上述传播规则，得到新的网络谣言传播模型(S2IR模型)的平均场方程为：

(3)

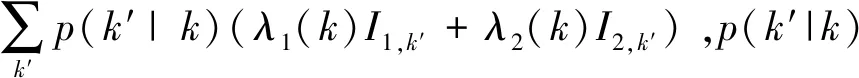
(4)

令Qk=Sk+I1 ,k+I2, k+Rk，将系统(3)左右分别相加可得：

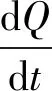
(5)

结合系统(3)和式(5)可以得到系统(3)的极限方程组：

(6)

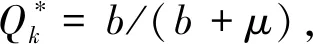
2 平衡点与基本再生数

借鉴传播学中基本再生数的定义，定义谣言传播的基本再生数为一个谣言传播节点在它传播谣言阶段使得谣言无知节点转变为谣言传播节点的个数，它决定无谣言平衡点的稳定性，并与谣言传播的最终规模有关。在这一部分将由正平衡点的存在性推导基本再生数的表达式，求出无谣言平衡点和有谣言平衡点，以及讨论几种常见的免疫策略。

为求解系统(6)的基本再生数，首先考虑稳态条件下的平衡解，令dSk/dt=0，dI1,k/dt=0和dI2,k/dt=0，容易求出方程组(6)的无谣言平衡点为

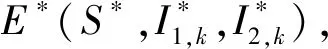
(7)

从Θ的表达式(4)可以看出，I1,k和I2,k的值取决于Θ。因此将式(7)代入式(4)可得到关于Θ的自治方程：

(8)

显然，Θ=0始终是该自治方程的一个平凡根，下面导出自治方程(8)存在正根的条件。易证F(0)=0，则方程(8)在Θ∈(0,λ1(k)+λ2(k)]内存在正根当且仅当

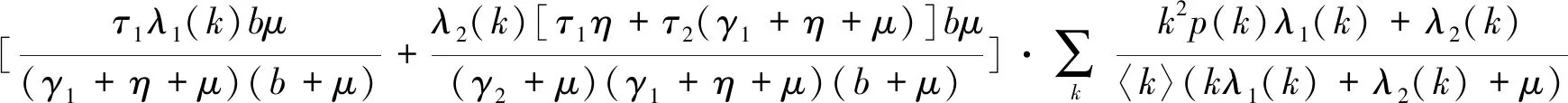
则F(Θ)=0在(0,λ1(k)+λ2(k)]上有正根的充要条件是当Θ=0时满足：

从而得基本再生数的表达式

由上述分析可得定理1。

定理1当R0<1时，系统(6)只有一个无谣言平衡点E0；当R0>1时，系统(6)除了E0之外，区域Γ中还存在唯一的有谣言平衡点E*。

下面给出全局稳定性的主要结论。

定理2当R0≤1时，系统(6)的无谣言平衡点E0是全局渐进稳定的；当R0>1时，系统(6)的有谣言平衡点E*是全局渐进稳定的。

利用文献[18]的定理4.2与4.3容易证明上述定理2，因此本文不再赘述。

3 谣言免疫策略

研究谣言传播模型是为了揭示谣言传播的特性以及影响传播过程的因素，并提出有效的控制谣言传播的方法以减轻或避免谣言传播造成的不良影响。在这一节中，基于本文提出的具有非一致传播率的S2IR谣言传播模型来分析随机免疫和目标免疫两种免疫策略的效果。

3.1 随机免疫

(9)

进而可以求出系统(9)的基本再生数：

将分离纯化后的菌株接种到对应淀粉培养基平板上，36 ℃培养48 h后将碘液滴加菌落上，有透明水解圈的菌落即判定该菌有产淀粉酶活力。

(10)

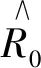
3.2 目标免疫

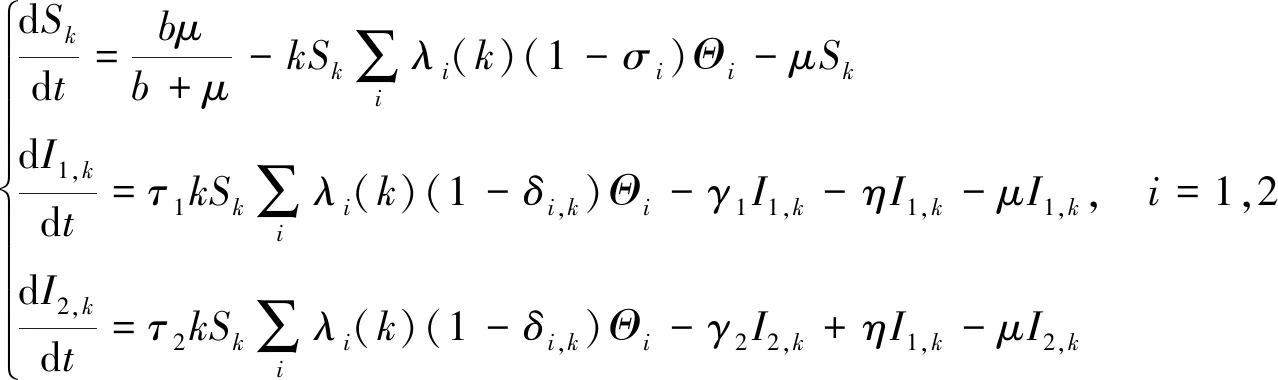
(11)

同理，可以推导出系统(11)的基本再生数为

(12)

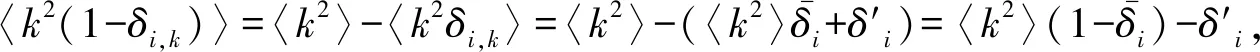
4 数值模拟与分析

由于大多数现实社交网络的度分布服从低幂律分布，不失一般性，以下在无标度网络上模拟社交网络中谣言传播过程。无标度网络采用BA模型的生成算法[21]，为便于仿真模拟，生成网络的最终规模取N=1 000， BA无标度网络[22]模型的相关参数为：初始节点数m0=2，每次进入新节点时新生成的连边数m=2，网络的平均度〈k〉=3.972，〈k2〉=45.318。本节所有实验结果均为独立进行了至少500次仿真实验的平均结果。由第1.1节分析，谣言信度函数α(k)的表达式可以是任意形式的减函数，以下仿真时采用的形式为：α(k)=k-θ，θ≥0。

4.1 仿真验证及参数分析

本节首先通过数值实验验证理论推导部分的准确性,然后分析相关参数对传播过程的影响。固定参数b=0.4，μ=0.04，θ=0.6，β=0.6，λ1=0.9，λ2=0.5，τ1=0.6，τ2=0.4，γ1=0.05，γ2=0.07，η=0.1，此时R0=6.918>1。图3a与图3b分别展示了10组不同初始值情况下两类谣言传播节点的密度变化情况，其中圆圈代表初始值，三角代表谣言传播稳态值。从图中可以看出不同初始情况下，各密度曲线均收敛于一点。图3c是在一组初始值I1(0)=0.001，I2(0)=0.001，S(0)=0.94，R(0)=0下各类节点密度的演化曲线，S、I1、I2分别达到0.3、0.08、0.17，与图3a、3b相吻合。

取参数取值b=0.4，μ=0.04，θ=0.6，β=0.6，λ1=0.16，λ2=0.09，τ1=0.6，τ2=0.4，γ1=0.08，γ2=0.12，η=0.1，此时R0=0.925<1。图4a与图4b分别显示了10组不同初始值情况下两类谣言传播节点的密度变化情况，三角代表谣言传播稳态值。从图中可以看出不同初始情况下，各密度曲线均收敛于一点，图4c是一组初始值I1(0)=0.3，I2(0)=0.3，S(0)=0.3，R(0)=0下各类节点密度的演化曲线，S、I1、I2分别达到0.9、0、0，亦与图4a、4b相吻合。

图3 谣言状态图Fig.3 State diagram with rumor

图4 无谣言状态图Fig.4 State diagram without rumor

图3c显示，当R0>1时，两类传播节点密度均逐渐上升达到峰值后开始下降，最后趋于稳定，即存在一个有谣言平衡点。图4c表明，当R0<1时，尽管两类传播节点初始密度较大，谣言传播节点密度仍逐渐下降，最后等于0，即系统只存在一个无谣言平衡点。

进一步探究R0>1时不同度的节点的演化情况，结果如图5所示，度大的节点中谣言传播节点的密度更大，即谣言在度大的节点之间传播速度更快，感染峰值更大。这主要是因为度大的节点虽然每次和一个传播谣言的邻居节点接触时被传染的概率较低，但其有更多的机会与传播节点接触，导致谣言在度大的节点之间传播速度更快、范围更广。

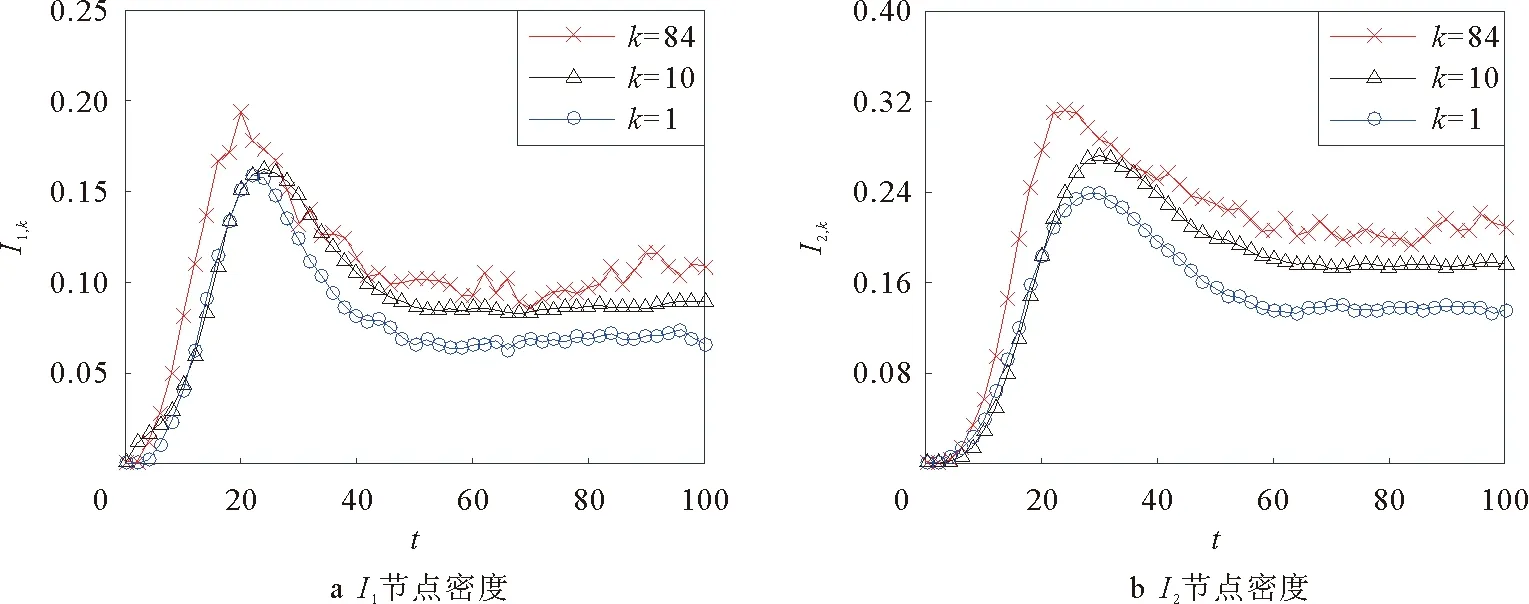
图5 度为k的谣言传播节点密度与时间的关系Fig.5 The relationship between the density of spreaders with degree k and time t

由传播率的表达式可知参数θ与β对传播过程有重要影响，当固定参数b=0.4，μ=0.04，λ1=0.9，λ2=0.5，τ1=0.6，τ2=0.4，γ1=0.05，γ2=0.07，η=0.1时，两类传播节点的总密度曲线如图 6a所示，可以看出当θ或β减小时，传播节点密度增大且传播速度变快。这主要是因为谣言信度函数及节点亲密度函数的存在，θ或β减小均会使接触传播率增大。当θ、β减小到0时即为传统的同一常数传播率，因此考虑谣言信度与节点亲密度时，谣言传播节点密度更小、传播速度更慢。遗忘率η、辟谣率γ1与γ2对控制谣言传播有重要作用，当固定参数b=0.4，μ=0.04，θ=0.6，β=0.8，λ1=0.9，λ2=0.5，τ1=0.6，τ2=0.4时，传播节点密度曲线如图6b所示，可以发现当γ1和γ2增大时，传播者密度明显下降，当η增大时，传播者密度也会下降，但增大γ1与γ2比增大η时下降的效果更明显；传播达到峰值与稳态的时间几乎相同。分析原因为：谣言传播具有爆发性，达到峰值所需时间极短，因此无论是辟谣率还是遗忘率增加均对其影响均不大，但会降低峰值和最终稳态密度。因此，若要快速降低谣言传播速度需从源头出发，减小传播率比增大遗忘率与辟谣率效果更好。

图6 不同参数取值下传播节点密度与时间的关系Fig.6 The relationship between the density of spreaders and time with different parameter values

4.2 基本再生数敏感性分析

对BA无标度网络中基本再生数的敏感性分析如图7所示，图7a中的参数取值为μ=0.04，η=0.1，θ=0.6，β=0.6，τ1=0.6，τ2=0.4，λ1=0.16，λ2=0.09，γ1=0.04，γ2=0.06，得R0=1时注册率为bc=0.081，R0随b的增大而增大。图7b中b=0.4，其余参数取值同图7a，得R0=1时移出率为μc=0.069，R0随μ的增大而减小。图7c中b=0.4，γ1=0.08，γ2=0.12，其余参数取值同图7a，得R0=1时遗忘率为ηc=0.054，R0随η的增大而减小。因此减小注册率b或增大注销率μ、遗忘率η均能使R0小于1，即能有效地控制谣言的传播。图7d参数取值为γ1=0.08，γ2=0.12，其余参数取值同图7a，当增大θ或β，R0能小于1，谣言能被控制住，这与第4.1节分析结果相同。

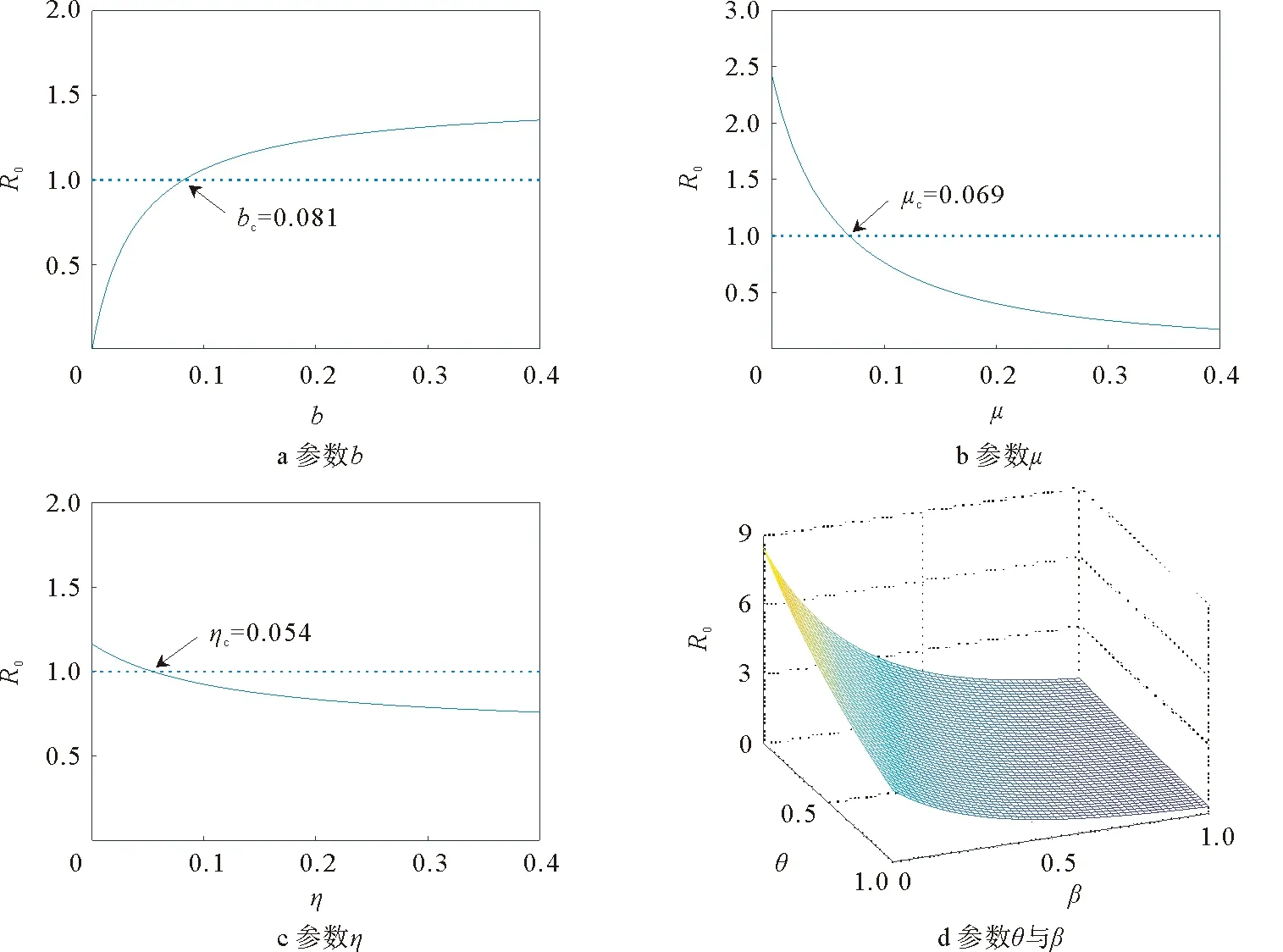
图7 R0随不同参数的变化Fig.7 R0 changes with different parameters

4.3 免疫策略效果分析

图8 不同免疫策略下R0随参数取值的变化Fig.8 R0 changes with different parameter values under immunization strategy

4.4 网络结构对传播的影响

4.4.1 仿真网络结构对传播的影响

分别在ER随机网络[23]、WS小世界网络[24]和BA无标度网络上仿真实验，3种网络节点总数均为N=1 000，网络平均度均为〈k〉=4，参数取值为b=0.4，μ=0.04，θ=0.6，β=0.6，λ1=0.9，λ2=0.5，τ1=0.6，τ2=0.4，γ1=0.05，γ2=0.07，η=0.1。分别随机选取1%的度为4的I1、I2两类节点作为初始传播节点，传播节点密度曲线如图9a所示，BA网络中传播节点密度的峰值最大且传播速度最快。这是因为BA网络的度分布服从幂律分布，网络中少数节点具有非常大的度(此类节点称为Hub节点)，一旦Hub节点被感染，其具有更多的机会与网络其他节点接触，传播速度会明显加快。

为探究网络平均度对谣言传播的影响，分别在平均度为10、20和30的WS小世界网络上仿真分析，网络节点总数均为N=1 000，分别随机选取0.1%的I1、I2两类节点作为初始传播节点，参数取值同图9a中参数取值，结果如图9b所示。发现WS网络平均度越大，传播节点密度的峰值越大且达到峰值所需时间越短。因为当网络平均度增大，节点间的接触传播率虽有所减小，但单位时间内节点之间相互接触的概率增大，由于社会强化效应的存在，致使网络中谣言传播速度加快。

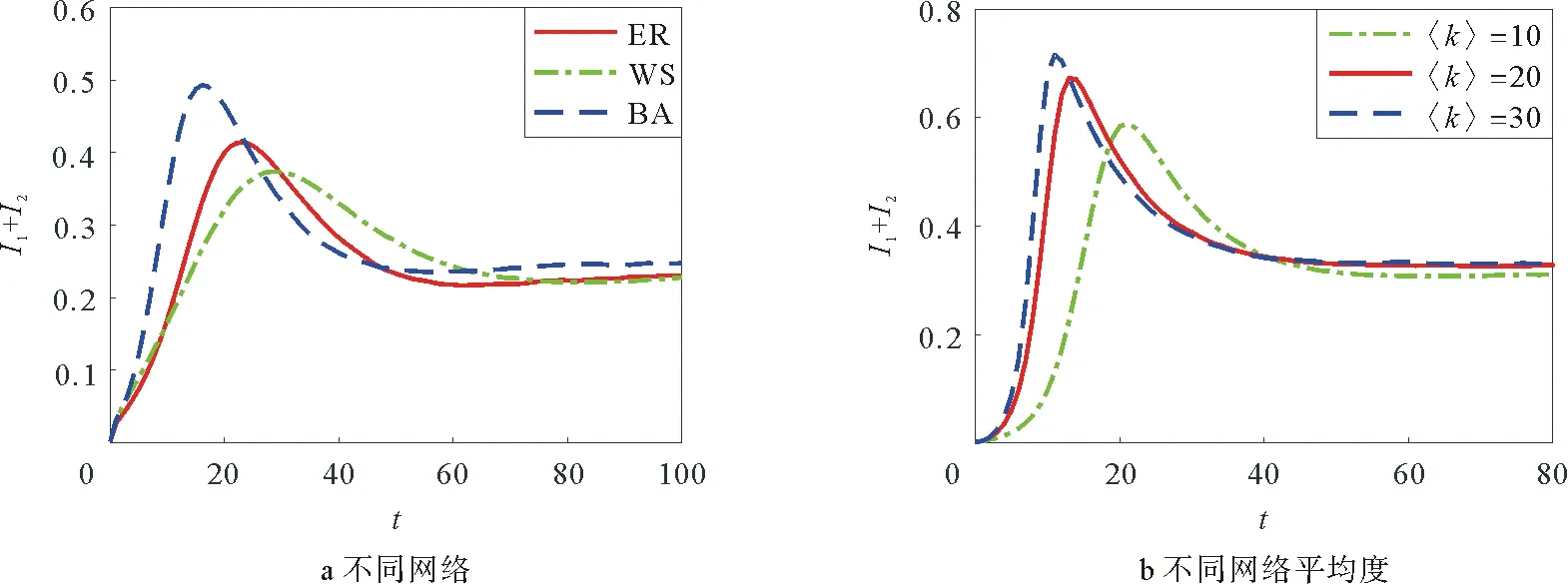
图9 传播节点密度与时间的关系Fig.9 The relationship between the density of spreaders and time t

表2 各网络统计特征Tab.2 Statistical characteristics of each network

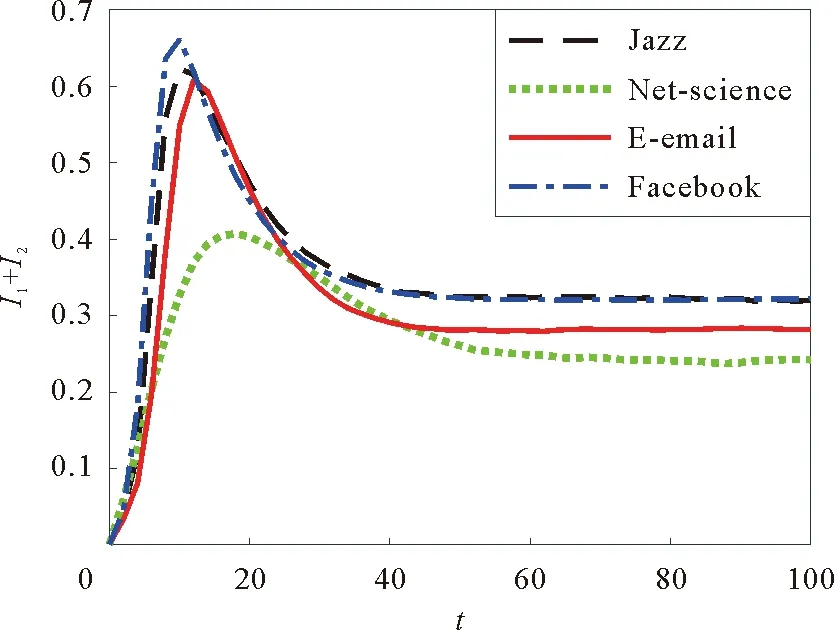
图10 传播节点密度与时间的关系Fig.10 The relationship between the density of spreaders and time t

4.4.2 真实网络结构对传播的影响

下面分别在四个真实网络：爵士音乐家合作网络(Jazz)、科学家合作网络(选择其中最大连通子图Net-science)、洛维拉·依维尔基里大学成员邮件通信关系网络(E-mail)和Facebook网络上仿真分析，相关参数与节点初始比例与图9a保持相同。表2列出了各网络统计特征。

仿真结果如图10所示，Facebook、Jazz与E-mail网络中I(t)的峰值远高于Net-science网络，且达到峰值所需时间小于Net-science网络，Net-science网络中I(t)的稳态密度小于其他网络，这是由于Net-science网络平均度较小。E-email网络中I(t)的稳态密度与传播速度小于Facebook与Jazz网络，是由于其网络平均集聚系数较小。事实上，Net-science网络中科学家的交流是基于科学家之间的研究方向与合作机会，其开放程度低于另外3个实际网络，因此实验结果与实际情况相符。对比图10与图9a可以发现真实网络中传播者峰值大体高于仿真网络，这与文献[16]结论一致，验证了本文模型的有效性。

4.5 对比分析

将同一常数传播率应用到S2IR模型与传统SIR模型进行对比实验，SIR的传播率、恢复率分别取S2IR中两种传播率、两种恢复率的平均值，并将本文非一致传播率S2IR模型与文献[14]中的非一致传播率SIR模型进行对比实验，结果如图11、图12所示，带*曲线均为非一致传播。图11反映，同一常数传播率下，S2IR模型与SIR模型相比，I(t)峰值更低，传播速度更慢；同一模型下，非一致传播率比同一常数传播率的I(t)峰值更低，传播速度更慢；本文非一致传播率S2IR模型与文献[14]中的非一致传播率SIR模型相比，I(t)峰值更低，传播速度更慢。图12反映，S2IR模型最终传播规模比SIR模型小，非一致传播率比同一常数传播率最终传播规模小。说明将传播节点分成完全信谣与轻度信谣，或是将同一常数传播率变为非一致传播率时，谣言传播速度与传播规模均减小。

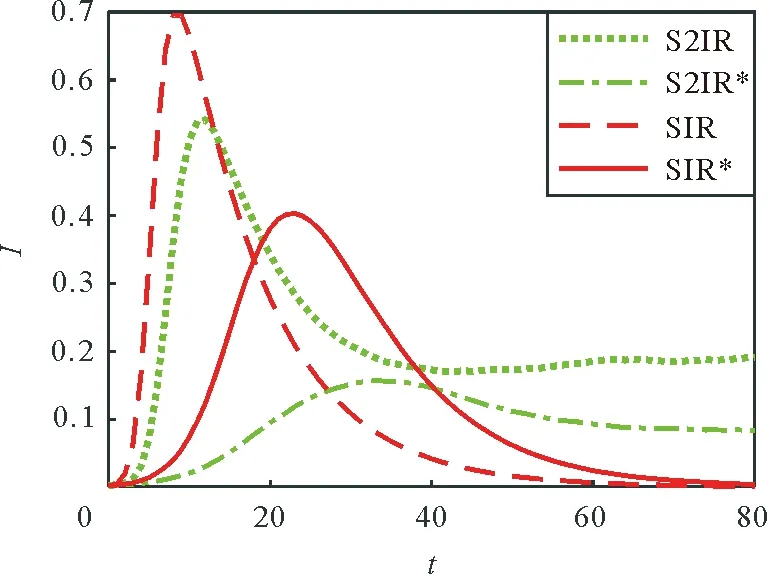
图11 传播节点密度与时间的关系Fig.11 The relationship between the density of spreaders and time t

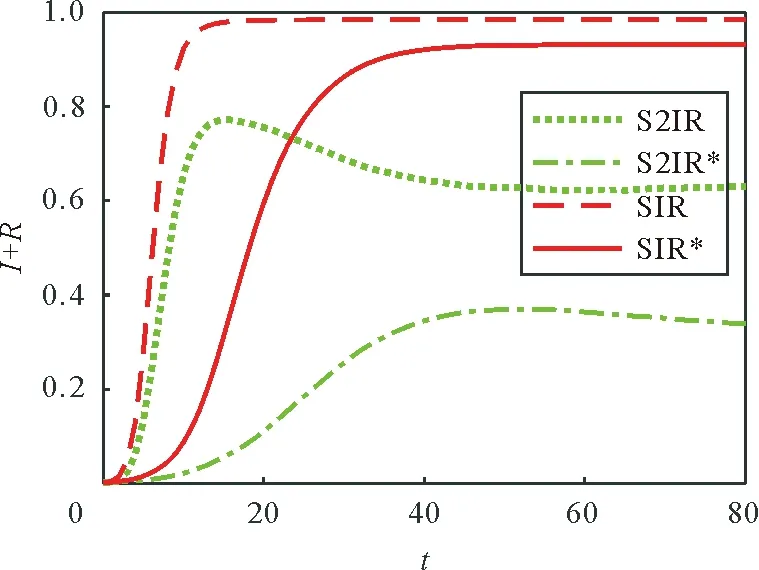
图12 传播规模与时间的关系Fig.12 The relation between the scale of spreading and time t

5 结论

考虑实际问题中谣言传播的(接触)传播率具有非一致性以及谣言传播节点的信谣程度存在差异的特点，本文结合复杂网络理论和平均场理论提出一个基于网络结构特征的社交网络谣言传播模型。该模型充分考虑了节点的度以及集聚系数，同时考虑了传播节点本身的传谣力度存在差异，更加符合现实社交网络中谣言的传播特点。利用建立的微分方程推导出了基本再生数，求出了随机免疫与目标免疫下的基本再生数、对两种免疫效果进行了对比分析。利用数值模拟验证了理论分析的正确性。在BA网络中仿真分析了网络谣言传播的特点，实验表明谣言更容易在度大的节点之间传播开。在随机网络、无标度网络和小世界网络中探究了不同网络结构和WS网络平均度大小对传播的影响，发现BA无标度网络中谣言传播最快，WS网络的平均度越大，谣言传播节点密度峰值越大。进一步在真实网络上仿真分析，验证模型的有效性，并对S2IR与SIR模型进行了对比分析。

通过分析相关参数对谣言传播的影响以及对基本再生数的敏感性分析，得到一些控制社交网络谣言传播的建议。参数θ或β增大会缩小谣言传播范围，θ和β一定时，谣言信度或节点亲密度减小均会缩小谣言传播范围；辟谣率γ1、γ2或遗忘率η越大，谣言传播规模越小，因此政府及相关部门应该加大辟谣力度，或者发布新的消息以增大遗忘率；必要时，控制用户注册率或增大注销率，谣言传播也能得以控制。若采取随机免疫，则增大随机免疫比例σ1或σ2能有效控制谣言传播；若采取目标免疫，则增大免疫率δ或减小截断值κ2能控制谣言传播。

本文仅考虑将谣言传播节点分为两类，实际上，谣言未知节点抵抗谣言的能力即其被传染的概率也存在差异，因此谣言未知节点也能进一步细分。沿着这个思路，我们下一步工作就是构造一个更加符合网络谣言传播的模型，以便更深入地发现网络谣言传播规律，进而提出更有效的控制网络谣言传播的建议。