多阈值随机汇池网络自适应估计性能研究

景文腾，耿金花，韩 博，段法兵

(青岛大学复杂性科学研究所，山东 青岛 266071)

0 引言

1 模型与方法

1.1 多阈值随机汇池网络模型

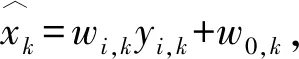
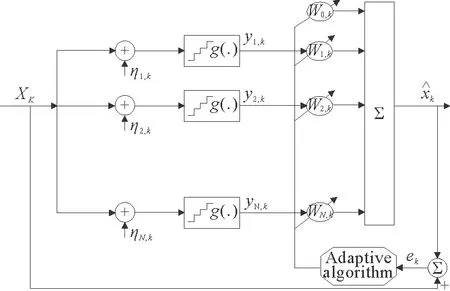
图1 多阈值自适应加权随机汇池网络模型Fig.1 Model of adaptive weighted stochastic pooling network with multilevel

1.2 理论分析

1.2.1 阈值划分及网络输出特征

在图1的随机汇池网络模型中，将每个并行量化器执行的运算记为g(.)，即阈值函数，为了易于实现，可以选择均匀地分布在[-1,1]的范围内2M+1个量化阈值

(1)

这里,j=-M,-M+1,…,0,…,M-1,M。那么当xk+ηi,k∈[θ2j-1,θ2j+1)时，量化器输出yi,k为

yi,k=g(xk+ηi,k)=j

(2)

此处定义θ-2M-1=-，θ2M+1=。每个量化器具有相同的输入xk，设其概率密度函数为fX(x)，与独立同分布的噪声ηi,k相加，设噪声的概率密度函数为fη(η)，均值为0，方差为依据式(1)和(2)，在k时刻，当θ2j-1≤xk+ηi,k<θ2j+1时，量化器输出yi关于输入信号xk的条件分布为

(3)

这里Fη(·)为噪声ηi,k的累积分布函数。

1.2.2 多阈值下的最优权向量与均方误差

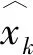
(4)

(5)

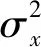
(6)

将式(6)带入式(5)，得最小均方误差为

(7)

在多阈值情况下进行具体分析，由式(3)可以得出条件均值和二阶矩

(8)

(9)

那么相关向量Pxy中

(10)

(11)

协方差矩阵Cyy的对角元素Cii和非对角元素Cil分别为

(12)

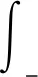
(13)

这里i,l=1,2,…,N且i≠l。利用协方差矩阵特征值及特征向量的分析[14]，最优权向量wo和最小均方误差可以简化为

(14)

(15)

1.2.3 多阈值随机汇池网络的Fisher信息

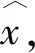
(16)

则网络的Fisher信息量为

(17)

由Fisher信息量求出后，可据此得出均方误差的下界

(18)

(19)

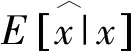
(20)

此处使用的节点数N为偶数，另外在n≠0的条件下还要满足n和i同为奇数或偶数，节点数为奇数的情况同理，Pn|x为每个量化器的输出的条件概率，可由式(3)得出。

2 实验分析

为探究多阈值情况下自适应加权随机汇池网络的估计性能，这里考虑随着阈值的数量增加网络的估计性能变化。例如划分为4级阈值时，M=2，当xk+ηk∈(-,-0.6)，阈值函数输出为-2，xk+ηk∈[-0.6,-0.2)，输出为-1，xk+ηk∈[-0.2,0.2)，当xk+ηk∈[0.2,0.6)，输出为1，xk+ηk∈[0.6,)，输出为2，同理可得其他阈值的情况。选取的输入信号xk分别为均值为0，标准差σx为1的高斯信号以及在[-1,1]上服从均匀分布的信号，加性噪声ηi,k选用均值为零，标准差ση的高斯白噪声。由于已知网络节点数对性能的影响[14]，网络数目N=10，依据式(8)～(15)得到结果如图2所示，由上自下分别对应阈值2、4、10、40和100的均匀划分方式。

注：由上自下分别对应阈值2、4、10、40和100。图2 均方误差随着输入噪声强度变化曲线Fig.2 Mean square error versus input noise levels for thresholds

由图2可以看出，均方误差随着噪声强度的变化存在随机共振现象，在一非零的最优噪声强度下，均方误差值为最小，且随着阈值数目的增加，最小均方误差值也在不断减小，证实了阈值数目的增加与自适应加权随机汇池网络的性能呈正相关关系。此外，图2还表明当阈值分级很多时(比如40级和100级)，曲线不再有明显的弯曲弧度，随机共振现象几乎消失，在图2b中，均匀分布的输入信号对阈值数目的增加更为敏感，在8阈值及10阈值的时候，加入噪声已经不会产生随机共振现象。这个原因是因为随着阈值划分级的增加，数字信号能够更加详细地量化模拟信号的变化，信息损失减少，因此人为增加噪声的方法只是在阈值划分级别较少时起到有益作用。

为探究不同阈值级别情况下的均方误差对于Fisher界的逼近情况，我们选取单阈值和多阈值两种情况进行分析。Fisher界即为Fisher信息量的倒数，任何无偏估计的方差至少要大于该界，也称为C—R下界，达到了Fisher界的估计为最小均方误差估计量。由文献[21]可知Fisher信息量表达式为J(x)=Nfη(x)2/[P1|x(1-P1|x)]，如图3所示。从图3中可以看出多阈值较单阈值情况下的随机汇池网络的均方误差更为接近Fisher界，从另一个方面印证了在最优加权随机汇池网络中多阈值分级的优越性。图4进一步研究了网络节点数增加对Fisher界的逼近情况，将噪声的标准差固定为0.6，可以看出，随着网络节点数的增加，均方误差同样随着阈值分级增加不断逼近Fisher界，但同时，均方误差距Fisher界仍有较大距离，因为Fisher信息量的大小与节点数目呈正比，且最小均方误差与Fisher界的距离还需要进一步通过阈值划分设计和噪声优化来改进。

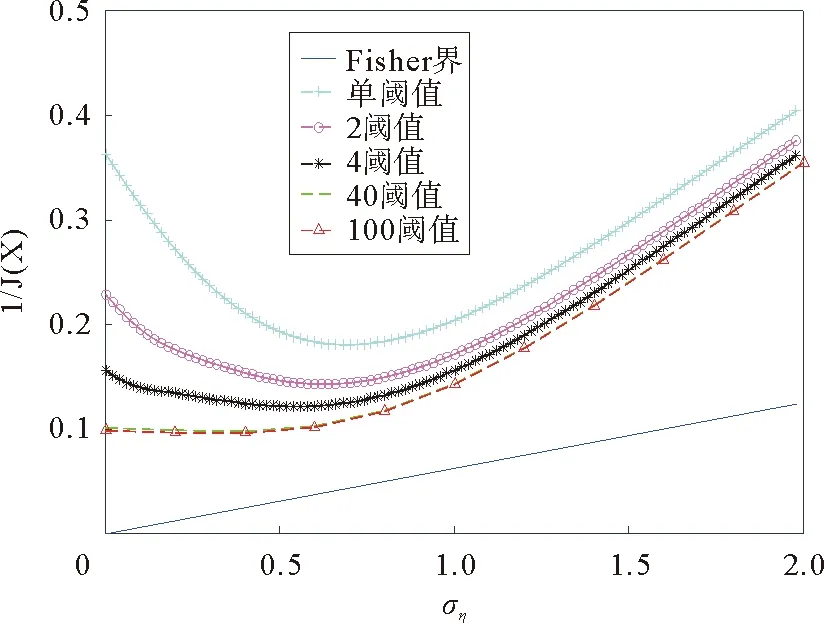
图3 不同阈值情况下随机汇池网络的均方误差与Fisher界随噪声强度的变化Fig.3 Fisher bounds and mean square error versus input noise levels for different thresholds

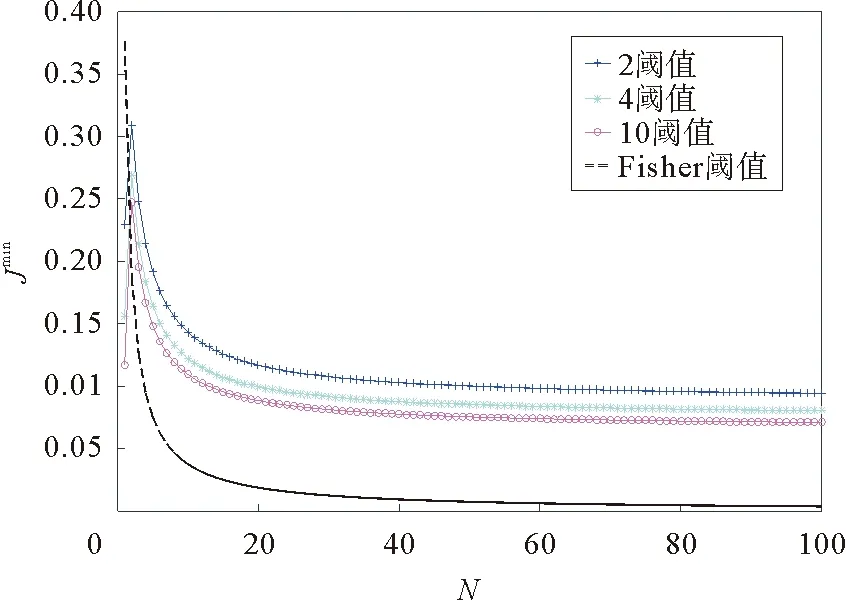
图4 不同阈值下随机汇池网络的均方误差与Fisher界随网络节点数目的变化Fig.4 Fisher bounds and mean square error versus network sizes for different threshold levels

3 结论与展望

本文研究了在多阈值自适应加权随机汇池网络的信号估计性能，以均方误差作为性能指标，理论上推导出了多阈值网络的最优权向量、最小均方误差和网络输出Fisher信息量表达式，实验结果表明随着阈值划分级别数量的增加，最小均方误差不断减小，当阈值数量增大到一定数目，噪声的有益性逐渐消失，因此人为加入噪声的方法在阈值分级比较少的时候才能起到积极作用。本文主要考虑了区间[-1,1]上的均匀阈值划分方案，没有考虑随机阈值、分组阈值以及阈值的区间可以优化调整的情况。因此，在多阈值随机汇池网络的信号估计性能研究中，从理论上论证出随机共振现象消失的原因以及推导噪声有益性的充要条件值得我们进一步深入探讨。