完全开放系统的幂律分布及其适用对象
2019-11-05李鹤龄王雅婷沈宏君
李鹤龄,王雅婷,杨 斌,沈宏君
(1.宁夏大学物理与电子电气工程学院,银川 750021;2.宁夏沙漠信息智能感知重点实验室,银川 750021)
0 引言

传统观念认为不同系综具有等价性,即认为由不同的系综推演的结果基本相同,因为曾有关于系综等价的证明[13]。因而通常在使用统计物理方法解决问题常使用最简单、方便的3种系综。如:微正则系综,它数值计算方便;正则系综理论分析方便;巨正则系综处理量子系统方便。但近年来,很多研究成果显示不同系综是不等价,如:具有长程关联的系统[14]、小系统[15]及相变点附近等[16]。这些不等价通常表现为微正则系综与正则系综的指数函数分布推导结果不一致,而微正则系综的推演结果通常是正确的,与实验结果接近吻合[15],耐人寻味的是微正则分布是等概论假设的结果,它是幂律分布零次幂的情景。再注意到:随着相互关联的增强、长程化和复杂化的研究对象的研究趋热,随机性系统的概率分布从指数函数走向幂函数。这样,对于不同相互关联的系统和外部环境选择合适的系综以及概率分布函数的具体形式就显得至为重要。因而必须充实统计物理方法中的系综理论及分布函数的具体形式。

1 基于Rényi熵的幂律分布

1.1 Rényi熵特性的简单描述
1960年匈牙利数学家Alfréd Rényi在Shannon熵基础上提出广义熵[29]或Rényi熵,其为
(1)
1)当q→1时,Rényi熵趋于Shannon熵
(2)

SR(A∩B)=SR(A)+SR(B)
(3)
这也正是现在通常将Rényi熵称为广延熵而Tsallis熵(不具有可加性)称为非广延熵的原因。事实上,现在常称为广延熵的Shannon熵和Rényi熵都会因所描绘的系统的广延或非广延性而表现出相应的广延或非广延性。
1.2 基于Rényi熵的完全开放系统的幂律分布
考虑一只做膨胀功的单组元系统,设所研究的系统处于热-粒子源的包围之中。系统与源之间可有力的、热的相互作用以及粒子的相互交换。源的巨大,使得这些相互作用不至于影响源的宏观状态。系统各微观态的粒子数Ni、能量Ei、体积Vi都可能不同。在系统和源达到平衡后,相应的平均值N、E、V都是一定的。以pi表示系统微观态i的概率,则应有:
(4)
由最大熵原理,考虑式(1)的Rényi熵在式(4)的约束,取拉格朗日函数:
(5)
其中λ0、λ1、λ2、λ3都为待定的拉格朗日乘子。令∂L/∂pi=0,得:
(6)
由归一化条件,得:
(7)
式(6)是幂函数形式的概率分布函数。按拉氏条件极值的方法,λ0和λk(k=1,2,3)要由式(4)的4个约束式和式(6)的W个方程共W+4方程来确定,但在物理学中,它们必须遵循热力学定律,因而由热力学定律来确定。如下分2步来确定拉格朗日乘子。
1)对应性法则的要求。
Rényi熵随q趋于1而趋于Shannon熵;由Shannon熵得到的是如下的指数分布[30]:
(8)
其中的α、β、κ也是拉格朗日乘子,在遵循热力学第零定律(热平衡)、第一(能量守恒)、第二定律(温度等于内能对熵的偏导数)的要求下,它们分别为
α=-μ/(kBT),β=1/(kBT),κ=P/(kBT)
(9)
并且
(10)
式(9)中μ为化学势,T为绝对温度,P为压强。
对应性法则要求:式(6)应随q→1而趋于式(8)的指数分布。所以其形式可选为[28]:
(11)
这样,可保证在q→1时,式(11)趋于式(8)。式(11)中
(12)
(13)
平均值为:
(14)
(15)
(16)
将式(11)代入式(1),可得熵:
SR=kBlnZ(1)+kBln[1+(1-q)αN+(1-q)βE+(1-q)κV]/(1-q)
(17)
进一步讨论后,在热力学系统应遵循热力学定律的要求下,上述(11)-(17)这一组热力学公式存在如下两个困难:
(1)∂S/∂E≠1/T=1/(kBβ),即内能对熵的偏导数不等于温度。
(2)热力学基本方程不能被推导出,即能量守恒定律不能反映出来。
上述两个困难的出现源于拉格朗日乗子的不恰当选择,所以,我们必须重新确定遵循热力学定律的拉格朗日乗子。
2)选取适当的拉格朗日乗子。
可筛选如下的拉氏乗子:
λ0=λ[1+(q-1)αN/q+(q-1)βE/q+(q-1)κV/q]
(18)
λ1=(1-q)λα/q,λ2=(1-q)λβ/q,λ3=(1-q)λκ/q
(19)
因为N、E、V都是平均值,是常量,式(18)和(19)是由新的4个拉氏乗子λ、α、β和κ替代了式(6)中4个拉氏乗子λ0和λk(k=1,2,3),因而这是可行的。将式(18)和(19)代入式(6),得:
(20)
由归一化条件知配分函数:
(21)
式(20)的完全开放系统的概率分布pi是关于变量Ni、Ei和Vi的幂函数形式,其中拉氏乘子α、β和κ是式(9)的形式,由平衡性质决定,N、E和V是平均值,求统计平均时,α、β、κ、N、E和V都不变。将式(20)和(21)代入式(1),可得:
SR=kBlnZ(2)
(22)
(23)
平均值:
(24)
(25)
(26)

对式(20)求微分,利用式(23)-(26),并注意到:Z(2)(α,β,κ)、N(α,β,κ)、E(α,β,κ)和V(α,β,κ)都是α、β、κ的函数。可得:
TdSR=dE+PdV-μdN
(27)
式(27)正是习惯的开系的热力学基本方程。且有:
(28)
自由能:
F≡E-TSR=E-kBTlnZ(2);dF=-PdV-SRdT+μdN
(29)
所以,式(20)及(21)的概率分布和配分函数、式(22)的熵、式(24)-(29)的平均值公式是满足热力学定律的完全开放系统的概率分布和热力学公式。
1.3 基于Rényi熵的其他系统的幂律分布
1.3.1 巨正则分布
利用式(20),可简单地获得其他分布。
巨正则系统的体积是常量。令(20)式中每个微观态的体积都等于常量,即Vi=V=常量,则式(20)变为
(30)
(31)
式(30)和(31)就分别是巨正则系统的概率分布和配分函数。将此二式代入式(1),得:
SR=kBlnZG
(32)
(33)
平均值:
(34)
(35)
同样得开系的热力学基本方程:
TdSR=dE+PdV-μdN
(36)
以及:
(37)
自由能:
F≡E-TSR=E-kBTlnZG;dF=-PdV-SRdT+μdN
(38)
明显地有:当q→1时,除了巨配分函数ZG之外,(30)、(32)、(34)和(35)分别转变为玻尔兹曼-吉布斯(Gibbs)统计的形式。
(39)
(40)
(41)
(42)
(43)
(44)
1.3.2 温度-压强分布
类似地,当令式(20)中的Ni=N=常量时,得:
(45)
(46)
SR=kBlnZI
(47)
(48)
(49)
(50)
同样可得类似于(36)-(38)的热力学方程和公式。
当q→1时,式(45)、(47)、(49)和(50)也趋于玻尔兹曼-吉布斯统计的形式。
当令式(20)中的Ni=N=常量、Vi=V=常量,或令式(30)中的Ni=N=常量,或令式(45)中的Vi=V=常量时,可方便地得到正则分布;其他分布也可方便得到,为避免重复,不赘述了。
显然,上述完全开放系统、巨正则系统、温度-压强系统等的概率分布和热力学公式是自洽的。
1.4 基于Rényi熵且不受热力学定律限制的复杂性系统幂律分布的简单形式
注意到统计物理方法早已被用于研究各种复杂系统,复杂系统一般不必受到诸如“守恒”、熵对内能的偏导数是温度的单值函数等热力学定律的限制。注意到式(24)-(26)的平均值公式都是自包含的,求平均值时难度较大。然而式(11)-(16)这套公式尽管不遵循热力学定律,但却不是自包含的。如果所讨论、研究的复杂性问题不涉及热力学两定律的要求,只要赋予N、E、V新的内涵,式(11)-(16)这套公式更简单、实用。因此,如下我们给出一套较易于求平均值的、可用于复杂系统的更一般的幂律分布和计算平均值的公式。前提是在不必遵循热力学定律时使用。
设描述复杂系统“总数量”特性的变量有l个,在W个系统随机状态中的第i个状态,由xki(k=1,2,…,l;i=1,2,…,W)描述。则xki的统计平均值为
(51)
按照上述方法可得概率分布函数:
(52)
(53)
因此,平均值为
(54)
熵:
(55)
式(52)-(55)中λk(k=1,2,…,l)是类似于物理学中的统计温度等具有某种“强度量”特点的复杂性系统的状态参量。
2 幂律分布不能用于近独立系统及广延系统的证明

众所周知:

3)幂律分布比指数分布更适用于长程相互作用或复杂的非广延系统。

定理若实函数p(x)是实变量x(-∞ p(x1)p(x2)=p(x1+x2) (56) 则,唯一不恒等于零的可微函数p(x)只能是指数函数p(x)=ax。式中a是不等于1的正常数(此处唯一性不考虑a的不同值)。 证明:由已知式(56),令x1=x,x2=dx。有 p(x)p(dx)=p(x+dx) (57) 因p(x)可微,分别有 p(dx)=p(0)+p′(0)dx (58) p(x+dx)=p(x)+p′(x)dx (59) 将式(58)、(59)代入式(57),有 p(x)p(0)+p(x)p′(0)dx=p(x)+p′(x)dx (60) 又x1=x,x=0时,由式(56),得 p(x)p(0)=p(x) (61) 要求p(x)非平凡,即p(x)不能恒等于零,应有 p(0)=1 (62) 则由式(60)得 p(x)p′(0)=p′(x) (63) 对式(63)积分,得: lnp(x)=p′(0)x+C (64) 式(64)中的C是待定积分常数。利用式(62),可得C=0。又因p(x)是非平凡的实函数,p′(0)必为不等于0的实数。设p′(0)=λ≠0,则式(64)去对数,成为 p(x)=eλx≡ax。(a=eλ,λ≠0,a≠1,a>0) 证毕。 基于最大熵原理和Rényi熵得到了完全开放系统的幂函数形式的概率分布、配分函数(式(20)和(21))、熵(式(22))和平均值公式(式(24)-(26))。 基于Rényi熵巨正则幂律分布、温度-压强等其他幂律分布、配分函数及平均值公式((30)-(50))也简单地得出,它们都是自洽的,且当Rényi熵中的参数q→1时,热力学函数、平均值公式等都回到了传统的玻尔兹曼-吉布斯统计的形式。 得到了可不必遵循热力学定律的、用于一般复杂性的系统较为简洁的幂律分布和平均值公式(式(11)-(17)或(52)-(55))。 严格证明了幂律分布不能用于忽略相互作用的系统及具有广延性的热力学系统。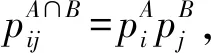
3 结论
