参照零模型的实证网络传播影响因素分析

周建云，刘真真，许小可

(大连民族大学信息与通信工程学院，辽宁 大连 116600)

0 引言

近年来多种传染病频繁爆发，给社会带来巨大的灾难并造成大量的人员损失，是人们关注的热点问题，因此研究疾病传播具有重要的意义和价值。通过构建疾病传播模型，研究复杂社会网络上的疾病传播规律，有利于分析影响疾病传播的因素，而且能够有针对性地采取防控措施，达到抑制疾病传播的目的。复杂网络中疾病传播的研究，尤其是网络结构对传播的影响，近年来受到众多研究人员的关注。早在1998年，Watts和Strogatz就指出“小世界效应”会加速传染病在网络中的传播[1]。Pastor Satorras和Vespignani发现，在度不相关的网络中网络的异质性对疾病的传播有着关键的影响；尤其是在大规模无标度网络上，不管传播阈值多低，疾病都会一直存在[2]。Eguiluz和Klemm指出，在SIS传染模型中，即使度分布的二阶矩发散，也存在非零的传播阈值，并提出度关联和高聚类系数可以抑制疾病在网络上的传播[3]。周冬梅等人基于双层网络的研究发现，层与层之间同配连接有益于信息的传播，而异配连接则会抑制信息的传播[4]。Liu和Hu发现，与随机均匀网络相比，在具有社团结构复杂网络中的疾病传播有较小的传染临界值和更大的稳态感染密度[5]。Huang和Li发现，疾病在具有社团结构的无标度网络中的传播范围要远远小于一般的无标度网络[6]。Zhou发现，在具有社团结构的网络中，随着传播速率的增加，感染密度会表现出稳态、不稳定振荡或周期振荡等不同特性[7]。王宁宁指出疾病更容易在无标度网络中传播，无标度网络社团之间的耦合强度不会影响最终的染病人数，但社团结构的存在会缩短疾病传播达到稳态的时间[8]。Wu和Liu研究指出，在无标度网络中，社团结构和高聚集系数是疾病传播的不利因素，将会抑制疾病在网络中的传播[9]。

以上研究中，大都分析复杂网络中单一结构因素对传播的影响，但是实证网络中某个统计特征的变化往往会导致其它很多特征的同步变化，而疾病传播的结果是多种因素共同作用的结果，现有研究中一般无法区分各因素的不同作用。在本文中，我们提出一种新的研究思路，将疾病传播模型与零模型相结合，讨论在多结构因素影响下(对应多种零模型)，何种结构因素对疾病传播起着至关重要的作用，从而更加全面和系统地分析网络结构特征对疾病传播的影响。具体地，根据实证社会网络构建出不同阶零模型[10]，在原始网络与零模型网络上进行疾病传播的仿真实验，比较不同零模型与原始网络之间的特征差异对传播有何影响。结果显示，网络中节点之间的最短路径是影响传播速度的最重要因素，该因素的影响要远远大于网络度分布(1阶特性)、度匹配(2阶特性)和聚类系数(3阶特性)；网络度分布是影响传播范围的主要因素。在增强和减弱度匹配特性零模型上进行传播仿真实验发现：同配系数与传播速度之间不具有强相关关系，而平均最短路径长度是影响传播速度的最重要因素。此外，社团结构的强度变化引起网络平均最短路径长度的改变，从而对疾病的传播造成影响，更加印证了网络平均最短路径长度是影响传播速度的最重要因素。

1 基于0-3阶零模型的传播分析

1.1 传播模型简介

经典的疾病传播模型有SI模型[11]、SIS模型[12]以及SIR模型[13]等。本文研究框架具有通用性，因此理论上可以使用本文框架研究任意传播模型在复杂网络中的传播。考虑到SI模型机制最简单，本文主要基于SI模型研究网络中的传播速度，同时基于SIS模型研究传播范围。在SI模型中，处于易感状态(Susceptible)的个体为易感染者，表明其当前时刻为健康状态，当其与处于感染状态(Infected)的感染者有接触时，易感染者以感染率β被感染，变为感染者；感染者不会变回易感染者。这种假设对于研究难以治愈的疾病或者突发疾病的短期爆发过程等都是合理的。SI模型的感染机制可由式(1)来描述：

(1)

其中，S(i)为初始时的易感染者，I(j)为感染者，I(i)表示S(i)被感染成为的感染者，右边的I(j)表示感染者不会变回易感染者。

表1 SI模型算法流程Tab.1 The flow chart of SI model

SI算法的流程如表1所示，其中，感染者数量为I，易感者数量为S，总数N=S+I；感染率β表示易感染者在单位时间被染病邻居感染的概率。在本文的研究中,初始时刻总是选取一个个体设为感染者(I=1)，剩余个体均为易感者(S=N-1)；设Δt=1。

SIS模型是基于SI模型的一种变形，在SIS模型中，节点被感染后将会以概率γ恢复成为易感转状态，之后与感染者接触时，仍以感染率β被感染。

1.2 0-3阶随机断边重连零模型

一般而言，使用网络零模型的主要目的是检测实证网络的非平凡特性，这就需要从粗糙到精确逐步逼近原始网络。文献[14-15]为了逐步逼近实证网络，根据原始网络的基本特性，将网络中的基本组成单元分成不同的小模块。不同阶数零模型之间并不是独立的，按照约束条件从少到多，存在一种包含关系，即0k⊇1k⊇2k⟺…(n-1)k⊇nk，任何一个n阶零模型都会包含n-1阶零模型的性质[16]。

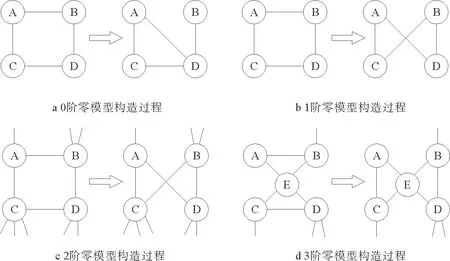
图1 0-3阶零模型的构造过程Fig.1 The construction process of 0-3k null models

在复杂网络中常用的零模型为0-3阶零模型，本文应用随机断边重连方法构建零模型[17]，图1展示了基于断边重连方法构造0-3阶零模型的具体过程。0阶零模型只需保持和原始网络相同的节点数和平均度。图1a为0阶零模型的构造过程，在原始网络中随机选择一条连边AB断开，并随机选择两个不相连的节点A、D，在两节点之间添加一条连边。1阶零模型主要是保证与原始网络具有相同的节点度分布(度序列)。图1b为1阶零模型的构造过程，若原始网络中存在节点A、B、C、D，且A与B相连，C与D相连，A和D不相连，B和C不相连；将AB和CD断开，使A与D相连，B与C相连，则保持了原始网络的度分布(度序列)不变。2阶零模型与原始网络具有相同的联合度分布，联合度分布是指每条边两端连接节点的度值数目(概率)。若m(k1,k2)为度为k1和k2的节点之间连边的总数，则p(k1,k2)=m(k1,k2)μ(k1,k2)/2m，其中，若k1=k2，则μ(k1,k2)=2；否则，μ(k1,k2)=1。图1c是2阶零模型的构造过程，保持网络的联合度分布不变，仅比一阶特性多了一层限制，即要求连边在随机置乱时，节点B与D具有相同的度值。3阶零模型与原始网络具有相同的联合边度分布p(k1,k2,k3)，就要求零模型网络和原始网络具有相同的开三角形和闭三角形分布。联合边度分布考虑到三个节点之间的相互连接性，主要有两种情况：一种是开三角形，即3个节点用2条边来连接称为pΛ(k1,k2,k3)；另一种是闭三角形，3个节点形成一个环称为pΔ(k1,k2,k3)。图1d是3阶零模型的构造过程，保持网络的联合边度分布不变，连边置乱后零模型和原始网络中的开三角形与闭三角形数量均相同。

图2 原始网络及0阶零模型的度分布Fig.2 The degree distribution of the original network and its 0k null model

1.3 实验结果与分析

本实验使用某企业的短信通讯数据集进行仿真实验，对应的实证社交网络反映了该企业内部的信息交互情况[18]。网络中包含2 111个节点，3 050条连边。图2是该原始网络及0阶零模型的度分布图，如图所示，原始网络的度分布具有长尾分布的特点，从图中能够看出0阶零模型缩小了网络度分布的异质性。由于1-3阶零模型均保持了原始网络的度序列特征，因此度分布和原始网络完全相同，故没有在图中显示。

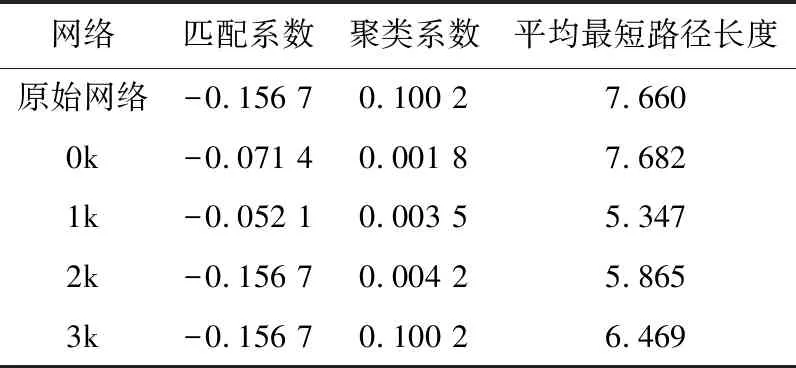
表2 网络特征统计量Tab.2 Network feature statistics

表2列出了原始网络和0-3阶零模型的其他结构特征(匹配系数、聚类系数和平均最短路径长度)。从表中可以看出，1-3阶零模型随阶数的上升与原始网络越为接近；而0阶零模型由于改变了度分布，致使其随机性最强，除了平均最短路径长度之外，其他特征与原始网络的差异最大。

首先，基于SI模型研究影响传播速度的关键因素。图3是原始网络和0-3阶零模型传染密度随时间变化的曲线图。这里设传染率β=0.2，传播时间T=80，曲线是实验200次取均值的结果。从图中可以看出，相对于高阶零模型，0阶零模型的传播曲线更加接近于实证网络。具体地，0阶零模型在初始阶段传播速度低于原始网络，而在t=30之后，这一情况发生了反转，0阶零模型的传播速度大于原始网络。而1-3阶零模型的传播速度总是大于原始网络，随着阶数的上升，传播速度下降，并且随时间传播的相对次序不变。随着阶数的升高，1到3阶零模型的传播速度越来越趋近于原始网络，这是因为随着阶数的升高，所生成的零模型网络与原始网络的结构差异也越来越小。

尽管1-3阶零模型的拓扑结构相对于0阶零模型，在很多方面更加接近于实证网络，但是0阶零模型的传播曲线却和真实网络更加相似。为了揭示出现这一现象的主要原因，图4显示了原始网络与0-3阶零模型中节点间最短路径长度的分布，横轴为最短路径长度，纵轴为该路径长度在网络中的概率分布。从图中可以看出最短路径长度在7以下时，1-3阶零模型曲线有序地在原始网络上方，而0阶零模型在原始网络的下方。在最短路径长度大于7时，这一情况发生反转，1-3阶零模型均在原始网络的下方且保持相对次序不变，表明1-3阶零模型的平均最短路径长度随阶数的上升而增加且都小于原始网络。此时0阶零模型相对于1-3阶零模型，它更加接近于实证网络，这也是0阶零模型和原始网络传播曲线特征比较接近的重要原因。由以上分析可知，在该实证网络中，网络中节点之间的最短路径是影响传播的最重要因素，该因素的影响要远远大于网络度分布(1阶特性)、度匹配(2阶特性)和聚类系数(3阶特性)。

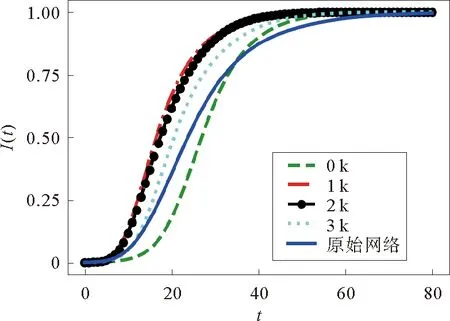
图3 0-3阶零模型及原始网络传播曲线Fig.3 0-3k null models and original network spreading curves

图4 最短路径长度的分布Fig.4 The distribution of shortest path length

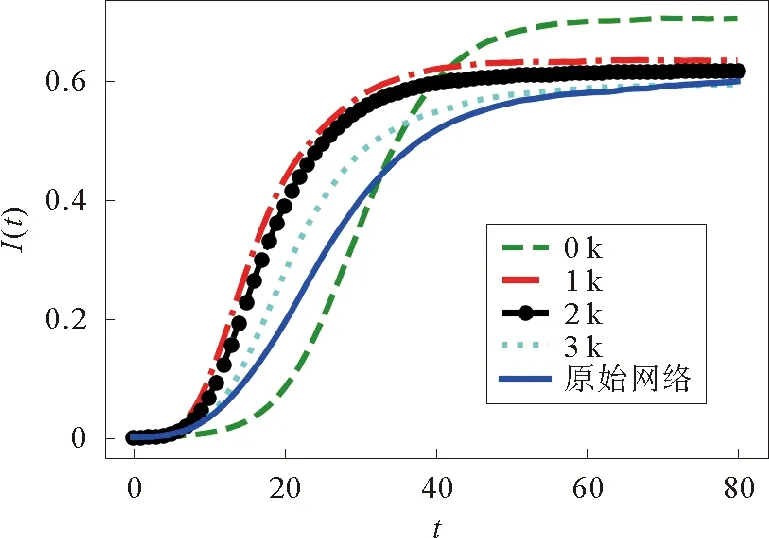
图5 SIS模型下0-3阶零模型及原始网络传播曲线Fig.5 0-3k null models and original network spreading curves in SIS model

然后，基于SIS模型研究影响传播范围的关键因素。图5是SIS模型下原始网络和0-3阶零模型传染密度随时间变化的曲线图。这里设传染率β=0.2，恢复率γ=0.09，传播时间T=80，曲线是实验200次取均值的结果。如图所示，0阶零模型网络的最终传播范围要显著高于1-3阶零模型及原始网络。具体地，在传播前期，1-3阶零模型的传播范围有序地大于原始网络，0阶零模型的传播范围显著小于原始网络。但是，随着传播时间的增加，当t>32后，0阶零模型的传播范围逐渐超过了原始网络和1-3阶零模型。当t>39后，0阶零模型的传播范围大于1-3阶零模型和原始网络的最大传播范围，并仍在快速增加，最终达到75%，显著高于其他网络(60%左右)。0阶零模型与1-3阶零模型及原始网络的本质区别是度分布不同，所以造成传播范围差异性的主要原因是网络度分布的改变。

2 基于匹配特性零模型的传播分析

2.1 面向匹配特性有倾向性断边重连零模型

在各种网络中，如果网络中度大的节点倾向于和度大的节点相连，度小节点倾向于和度小节点相连，这种倾向性即为度匹配的正相关性。如果度小节点倾向于和度大节点相连，这种倾向性即为度匹配的负相关性。可以使用匹配系数(Assortativity coefficient)[19]来度量网络的匹配特性，如果匹配系数r为正值，代表具有相同度值的节点之间有某种协同关系，网络具有正匹配特性；如果匹配系数r为负值，表示具有不同度数的节点间有某种联系，网络具有负匹配特性。

如果想改变实证网络的度匹配特性，就需要有倾向性地进行断边重连来构造同配或异配网络。如图6所示，原始网络a中有A、B、C、D四个节点，其中节点A与C相连，B与D相连，相连节点之间的度有一定差距但相差不大，属于中性网络。如果将原始网络的度大节点A和度大节点D相连，度小节点B和度小节点C相连(如图6b所示)，就增强了网络的同配特性。将这一过程反复进行，就可以生成强同配网络。相反，将原始网络的度最大的节点A和度最小的节点B相连，其余节点相连(如图6c所示)，就增强了网络的异配特性，反复进行就可以生成强异配网络。

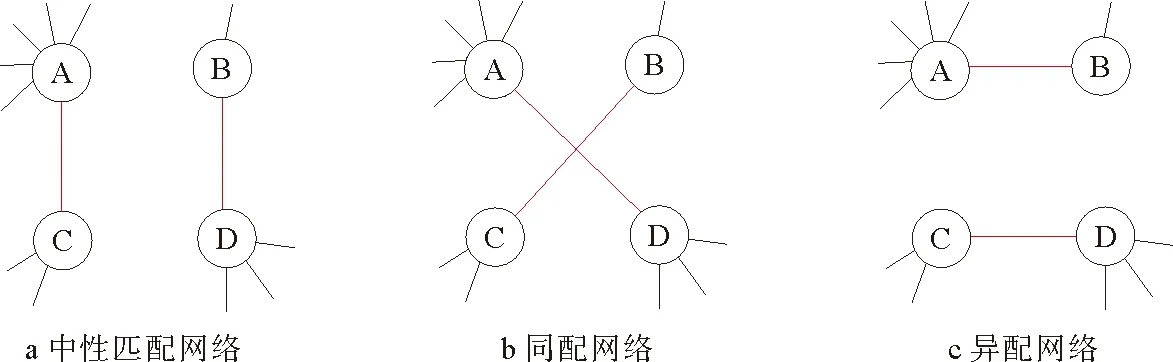
图6 复杂网络中3种不同的度匹配模式Fig.6 Three degree assortativity patterns of complex networks

使用上述有倾向性的断边重连算法生成强同配网络和异配网络后，就可以研究网络拓扑结构对度度相关特性的约束以及这种约束对传播有何影响。

2.2 实验结果与分析

图7为原始网络及同配零模型、异配零模型网络的传播曲线图，r是匹配系数，正值表示网络为同配网络，负值表示网络是异配网络。根据左焘等以前的研究结果可知：同配系数越大的网络，传播速度越慢，即同配系数的增大将会对疾病传播起抑制作用[20]。然而每个网络具有不同的特点，从图中的实验结果来看与上述结论并不完全相符，匹配系数的变化并没有导致比较有规律的传播结果。

图7 匹配特性零模型传播曲线Fig.7 The propagation curve of null models with different Assortativity

参照零模型的方式可以循序渐进分析出度匹配特性由弱到强的整个过程中对于传播的影响。图8a是匹配系数随置乱次数的变化曲线，纵轴是匹配系数，横轴是置乱次数，其中n是网络中连边的数量，负数代表网络进行异配置乱，正数代表进行同配置乱。图8b为传播速度随置乱次数的变化情况，纵轴是传播速度，定义为单位时刻传染的人数，这里取传染90%的节点与所用时间的比值作为传播速度，横轴是置乱次数。如图8a所示，匹配系数随置乱次数单调增加。理论上，疾病的传播速度应与图8a相对应，即与同配系数呈负相关关系，但是从图8b能够看出与上述结论存在明显差异。为了探究这一现象，接下来我们计算了匹配特性零模型的平均最短路径长度，分析到底是什么因素起主导性，对疾病传播的速度有着重要影响。图8c是匹配特性零模型的平均最短路径长度随置乱次数的变化曲线，纵轴是平均最短路径长度，横轴是置乱次数。从图中可以看出，改变匹配特性零模型的置乱次数会改变网络的平均最短路径长度，但其与置乱次数并无明显相关性。为了进一步讨论平均最短路径长度的改变对传播速度的影响，图8d给出了传播速度与平均最短路径长度的对应关系。从图中可以看出，平均最短路径长度与疾病传播速度具有强相关关系，呈现负相关性。至此，可以得到以下结论：在匹配特性零模型上的疾病传播，多因素共同作用下，平均最短路径长度相对于度匹配特性对疾病的传播速度起着主导作用。

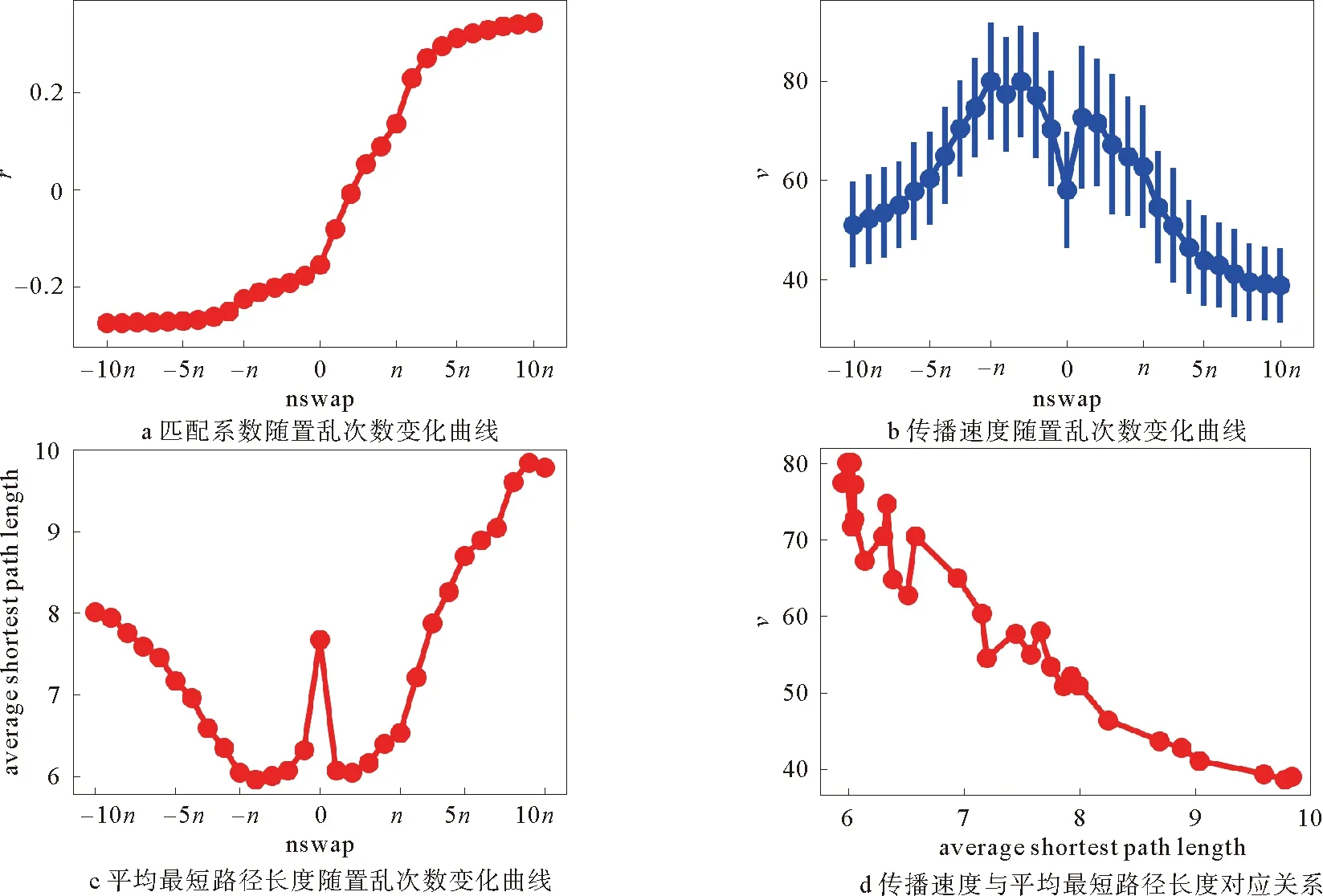
图8 不同匹配特性零模型对应的传播曲线Fig.8 TheSpreading curves corresponding to null models of different assortativity

3 基于社团结构零模型的传播分析

3.1 增强和减弱社团结构零模型

社团结构一般会呈现出社团内部节点之间连接稠密、属于不同社团的节点之间连接稀疏的特点。如果要增强原始网络的社团结构，就需要减少社团之间的连边，增加社团内部的连边。增强社团结构的零模型构造过程如图9所示。首先将原始网络划分为多个社团，然后在保持其它连边结构不变的情况下，将两个社团之间的连边交换为社团内部节点之间的连边。如图9a中所示，将社团A和社团B间的两条连边A1-B1与A5-B3断开，然后分别将社团A中的两个节点A1与A5相连，将社团B中的两个节点B1与B3相连，得到的网络拓扑结构如图9b所示。

基于断边重连的减弱社团结构零模型构造过程是将上述过程反过来。首先将图9b中社团A内部的连边A1-A5和社团B内部的红色连边B1-B3断开，然后将社团A和社团B间的节点A1与B1相连、A5与B3相连，重新连接后的结果如图9a所示。增强或减弱社团结构的零模型可以有效在保持真实网络拓扑结构基本不变的情况下，增强或减弱社团结构特性。

3.2 实验结果与分析

图10为原始网络及增强和减弱社团结构零模型网络的传播曲线图。Q是模块度值[19]，它是衡量网络社团结构强弱的指标，Q值越大，表示网络中社团结构越强。从图中可以看出，Q值越大的网络，疾病的传播速度越慢，全部节点感染所用时间越长。主要原因是，随着社团结构的增强，社团内连接的紧密性增强了，社团间的连接强度减弱了，这使得疾病在社团间的传播变得困难，从而减慢了疾病在网络上的传播速度。相反，减弱网络中的社团结构，也会对传播速度及全部节点感染所用的时间有影响，即社团结构越弱，传播速度越快，全部节点感染所用的时间也越短。为了揭示出现这一现象的具体原因，图11给出了原始网络及增强和减弱社团结构零模型的节点间最短路径长度分布图。从图中可以看出，Q值越大，网络的平均最短路径长度越大；Q值越小，网络的平均最短路径长度越小。因此，增强和减弱社团结构强度对于疾病传播的影响可以归根于网络中节点间最短路径长度的变化。

图9 增强和减弱社团结构的零模型Fig.9 The null models of increasing and weakening community structure

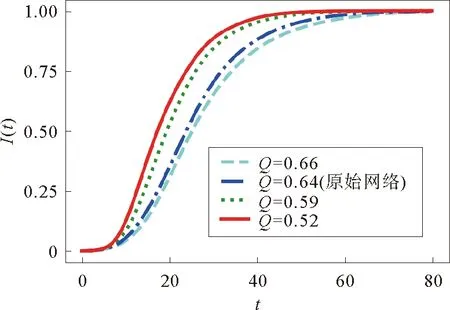
图10 原始网络及社团零模型传播曲线Fig.10 The spreading curves of community null models

图11 最短路径长度分布Fig.11 The distribution of shortest path length

4 结论

在实证网络中很难精确分析单一的网络结构参数对于传播的具体影响。本文通过引入网络零模型，探讨原始网络和零模型网络之间拓扑结构的差异对疾病传播的影响。基于原始网络构建0-3阶零模型，并且在原始网络和零模型网络上进行传播仿真实验，分析不同网络之间的传播差异。在0-3阶零模型上进行传播仿真实验，比较网络结构差异与实验结果可知：网络的平均最短路径长度是影响疾病传播速度的关键因素，而度分布的变化是影响传播范围的主要原因。在基于匹配特性零模型的传播仿真实验中发现：网络的匹配特性不是影响传播的主要因素，而网络的平均最短路径长度是影响传播的关键性因素。网络中社团结构强度的改变，使得网络的平均最短路径长度发生改变，所以社团结构对疾病传播的影响实际上是网络平均最短路径长度的改变造成的，网络的平均最短路径长度越短，传播速度越快。