对一道中考题的模式、策略、本质的探究——基于贵阳市2019年中考几何压轴题的探究

☉贵州省贵阳市乌当中学 邓 清

☉贵州师范大学 陈 丽

著名数学家、哲学家怀特海曾提出“数学是模式的科学”的观点，提出“数学的本质特征就是在模式化的个体抽象的过程中对模式进行研究”.因为数学的研究对象，即概念和命题，都是对客观现实或数学现实的一种抽象，因此它们都是一种“模式”.学生在面临一个数学问题时，总会将问题与已认知结构中的问题模式进行比较，通过正确识别问题模式，迅速缩小对问题的搜索范围，减小思维的强度和负荷.

中考压轴题侧重考查学生对数学知识点的深度综合和对数学思想方法的灵活运用，常常需要较高的思维负荷和较强的综合应用能力，但其包含的问题本源又常常紧扣学生的已有认知.教师在向学生讲解此类问题时，不应该直接给出问题的解决策略，而应尽量挖掘问题中所蕴含模式的背景，将考题与学生认知结构中的已有问题模式联系，让学生自己得出问题解决的策略，如此，能促进学生数学思维的自然生成与发展.同时，教材是教师上课之本、中考命题之本，也是学生数学认知之本.学生认知结构中的问题模式，大多来源于教材中例题和习题的呈现.本文以2019年贵阳市的一道中考几何压轴题为研究对象，先探寻试题中所蕴含的问题模式在教材中的体现，以此作为思维的逻辑起点，逐步提高解题策略的思维层次，从多个视角提出解决该问题的不同方法.

一、试题呈现

图1

（贵阳市2019年中考数学第15题）如图1，在矩形ABCD中，AB=4，∠DCA=30°，点F是对角线AC上一个动点，连接DF，以DF为斜边作∠DFE=30°的直角三角形DEF，使点E和点A位于DF两侧，点F从点A到点C的运动过程中，点E的运动路径长是____________.

评析：解决该问题的关键是能感知并证明点E的运动轨迹，需要学生根据图形运动变化规律，抓住其中不变的特点.点E是随着点F的运动而运动的，根据已知条件不难知道，在运动变化中，∠EDF=60°、DE=这两个特点是不变的.如何引导学生想到解决此问题的办法，或者学生解决该问题可能的逻辑起点是什么，需要从学生的认知结构中可能存在的问题模式进行分析.

二、教材中的问题模式的探寻

北师大版2014年版教材初中数学八年级第89页呈现了这样一个问题：

（第三章复习题第11题）如图2，点D在等边三角形ABC的边BC上，将△ABD绕点A旋转，使得旋转后点B的对应点为点C.小明是这样做的：如图3，过点C画BA的平行线l，在l上取CE=BD，连接AE，则△ACE即为旋转后的图形，你能说明这样做的道理吗？

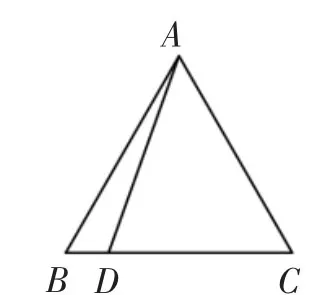
图2

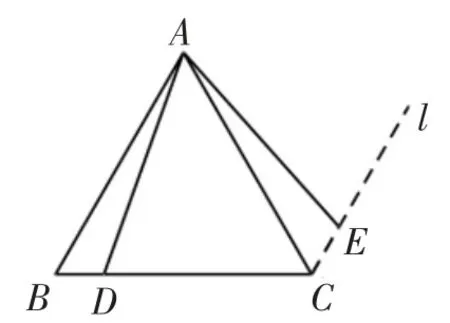
图3

这一复习题实质上是通过证明三角形全等说明△ABD绕点A旋转后，点D的对应点E恒在平行线l上.该问题的结论可进一步概括为：点D在等边三角形的边BC所在的直线上运动时，将线段AD绕点A沿逆时针方向旋转60°后，点D的对应点恒在与AB平行的直线l上运动.教材中这一复习题与上面中考试题的模式如出一辙，学生在解决这一复习题时，如能得到教师的适当引导，在认知结构中形成一种问题模式，就能形成解决上面中考试题的思维.

三、解题策略的形成

解法1：借助已有模式，构造等边三角形.

该试题通过添加辅助线构造等边三角形后，可以得到和教材习题相同的模式，借助这一问题模式，得到以下解决办法：

如图4，记AC的中点为O，过点O作直线l//AD，延长DE交直线l于点F′，连接DO.

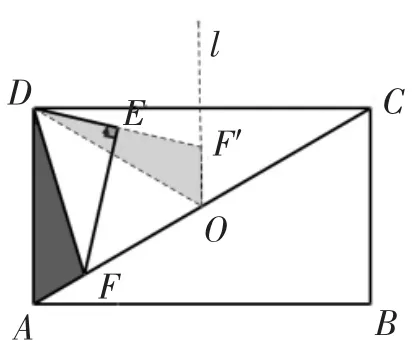
图4

易知DO=AO，∠DAO=60°，则△OAD为等边三角形.

根据∠ADO=∠FDE=60°，可得∠ADF=∠ODF′.又因为AD=OD，∠DOF′=∠DAF=60°，所以于是可认为DF′为DF绕点D沿逆时针方向旋转60°得到的，即点F的对应点F′恒在直线l上运动，且始终满足OF′=AF，所以点F′运动路径的长度等于点F运动路径的长度AC=而DE=则点E的运动路径为点F′运动路径的一半，即

解法2：观察轨迹特点，构造相似三角形.

解法1借助教材中的问题模式，符合学生的认知特点，是学生比较容易接受的一种解决方法.问题解决后，引导学生反思，解决该问题的关键是知道点E在平行于AD的直线l上运动，那么可以通过证明点E到直线AD的距离为定值来说明直线l//AD.

如图5，过点D作DM⊥AC于点M，过点E作EN⊥AD于点N.

根据NE∥DC，可得∠CDE=∠DEN.

由于∠CDE+∠FDA=30°，∠MDF+∠FDA=30°，所以∠CDE=∠MDF.

则∠DEN=∠MDF.又因为∠DNE=∠FMD=90°，所以因此，即NE=DM=DC=1.

因此点E到直线AD的距离为定值，所以点E在一条平行于AD的直线上运动.

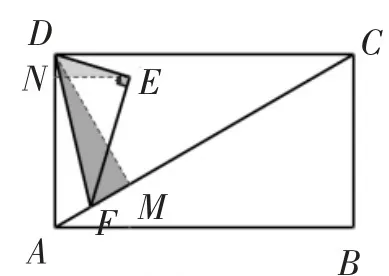
图5

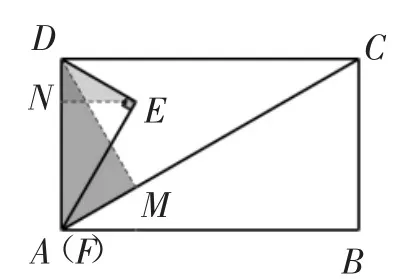
图6

当点F与起点A重合时，如图6，∠EDN=∠EDF=60°，所以；当点F与终点C重合时，如图7，∠EDN=30°，所以所以点E运动路径的长度为

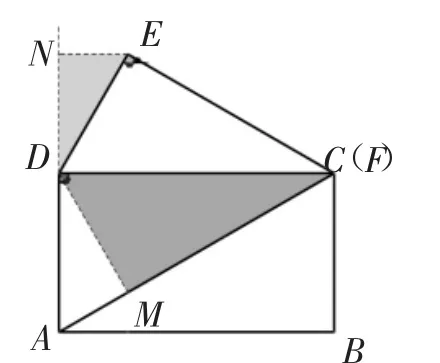
图7

图8

解法3：构造等腰三角形，寻找相同轨迹点.

解法4：寻求问题本质，形成高阶思维.

观察点F与点E的运动过程，实质上是一个图形的旋转及拉伸变换的过程.基于此，可以运用点的旋转坐标公式和拉伸坐标公式来研究点E的运动轨迹.

如图9，以点D为坐标原点，建立平面直角坐标系.

因为在旋转变换中，始终满足∠EDF=60°，且DF=2DE，可设点E的坐标为（x，y），DF的中点E′的坐标为（x′，y′）.点E′（x′，y′）是由点E（x，y）顺时针旋转60°得到的，根据旋转坐标公式，可得

图9

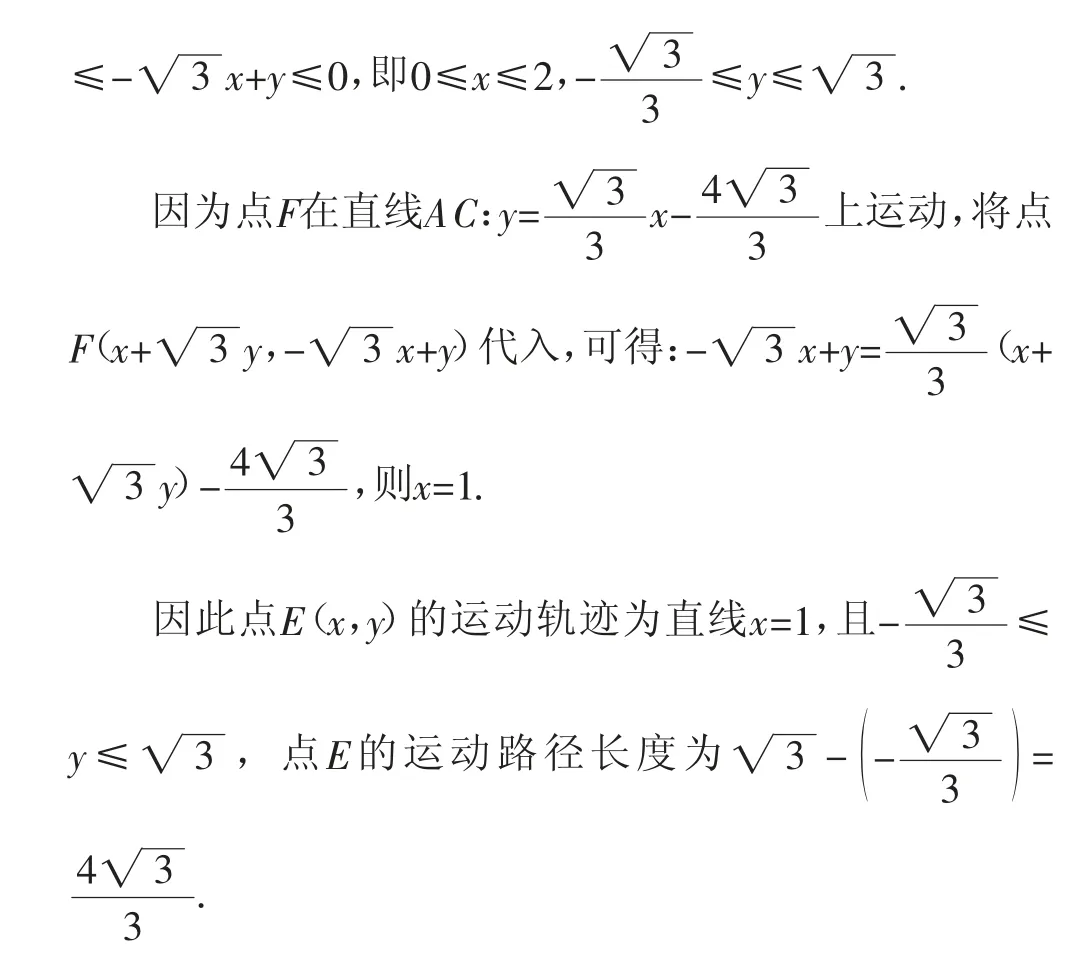
四.结论推广

解法4 体现了此类问题的本质，即如果点F与其对应点E存在这样的对应关系：存在一个定点O，使得∠EOF为一个定值，且为定值，当点F在一条直线上运动时，点E也在一条直线上运动.为了探寻两个动点运动轨迹的关系，根据以上中考试题的解决过程和得到的结论，归纳、推广得以下结论，并进行证明.

结论：如图10，在平面内，若点F与其对应点E存在这样的对应关系：存在一个定点O，使得∠EOF为一个定值θ，且为定值，当点F在一条长为m的线段上运动时，若该线段所在直线方程为Ax+By+C=0，则点E的运动轨迹也是一条线段，且该线段的长为λm，线段所在直线方程为（Acosθ-Bsinθ）x+（Asinθ+Bcosθ）y+λC=0.

证明：对于轨迹长度的证明，可采用上面的解法4的思路，在线段OE上取一点F′，使得OF′=OF，则点F′的轨迹长度等于点F的轨迹长度，再根据相似三角形的对应边成比例关系，不难得出点E运动轨迹的长度与点F′运动轨迹的长度之比为，因此点E运动轨迹的长度为λm.

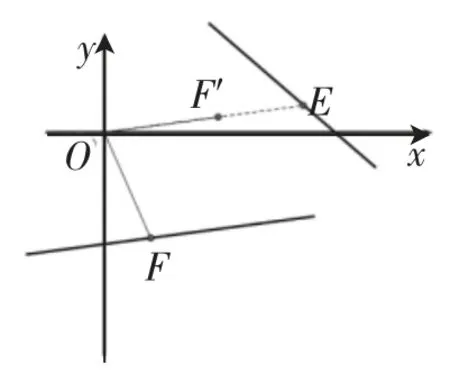
图10

五、结束语

本文以一道中考试题为对象，通过在教材中对问题模式的探寻，以递进和螺旋上升的形式对试题多种解题策略进行探究，最终以蕴含高阶思维的解题策略推广为一般结论.研究过程中，既充分考虑学生的认知结构，也注重思维形成的逻辑，有利于学生数学思想的生成和发展，促进学生数学素养的形成.