无导引头也无惯导导弹的协同制导
2019-10-31赵建博杨树兴熊芬芬
赵建博,杨树兴,熊芬芬
1. 北京理工大学 宇航学院,北京 100081
2. 西安现代控制技术研究所,西安 710065
寻的制导系统由于可实现导弹的“发射后不管”,故作为末制导领域的研究热点得到了广泛关注[1]。近年来,基于寻的制导系统的制导律研究中有很大一部分是为了实现导弹碰撞角约束,例如:采用有限时间收敛原理[2-8]以及动态逆控制[9]等。导引头作为寻的制导系统的重要组成部分往往造价昂贵。因此,有必要对无导引头导弹的制导问题进行研究以降低制导系统的成本。
无导引头导弹的制导研究尚处于起步阶段,而现有研究成果主要可分为两类:① 采用外部制导方案,即地面站实时控制导弹的飞行弹道从而实现命中[10-11]。然而,这种制导方式由于需要地面站协助,故无法实现导弹的“发射后不管”,并且容易暴露地面站的位置;② 采用协同制导方案,即由带有导引头的导弹作为领弹,从而带领其余无导引头导弹对目标进行攻击[12-14]。这种制导方式还可解决多枚导弹分别装备有不同种类导引头,而其中一些因受到干扰而失效的情况。上述协同制导方法均依赖于导弹之间的实时通信及导弹的绝对位置可精确测得。然而,导弹一般采用组合导航技术进行定位,必然会存在位置估计误差。针对此问题,作者团队[15-16]设计了无导引头导弹在考虑定位误差的情况下仍可精确命中目标的协同制导律。然而,由于导弹之间仍需要实时通信,故无法实现无线电静默攻击,且通信内容很有可能被敌方截获与干扰,降低了导弹的威胁性。因此,针对静止点目标,作者团队[17]利用无导引头导弹对有导引头导弹的测量信息,提出了一种不需要导弹间实时通信以及精确定位的分段式协同制导策略,并通过设计协同制导律实现了上述策略。然而,所设计的协同制导律仍需要惯性导航元件(惯导)提供测量信息,而装备较高精度的惯导也极大增加了导弹的成本。
为了解决上述问题,本文基于集中式“领弹-从弹”协同制导架构,提出可为无导引头也无惯导的导弹(从弹)安装两个相对廉价的捷联探测器(无线电探测器除外),分别对安装在一枚有导引头导弹(领弹)弹身上的两个靶点进行探测。由于上述探测器的探测目标是弹群中的导弹,故相比于导引头更加廉价[17]。此外,探测器采用捷联的方式减小了其体积与重量,更利于工程应用。对于从弹对领弹有依赖性的问题,为了提高领弹的生存能力,可在工程应用时为领弹安排额外的导弹进行保护,而参与保护的导弹可采用现有制导方法[18]。
通过两个探测器的测量,从弹仅可获得两组探测器相对于靶点的视线距离以及此视线相对从弹弹体纵轴的夹角。然而,由于从弹不具有惯导,故无法获得其姿态角信息,即意味着由捷联探测器测得的相对于从弹弹体系的视线角信息无法被转化为相对于惯性系的视线角,故现有的绝大多数制导律(例如:比例导引)均无法应用于无导引头也无惯导的从弹。
因此,在集中式“领弹-从弹”的协同制导架构下,本文进一步为无导引头也无惯导的从弹设计了相应的协同制导律,以实现其在不依赖导弹间实时通信与导弹绝对位置信息情况下的“发射后不管”。针对静止点或面目标,分别采用一般的负反馈控制方法、有限时间收敛原理以及动态逆控制为从弹设计了3种末制导律,均可实现在领弹命中目标时从弹速度方向指向其攻击目标。在此之后,从弹只需要进行直线飞行(即理想条件下的无控飞行)即可实现对其攻击目标的精确命中。
本文研究内容安排如下:第1节给出了将探测器的测量量作为状态变量建立的从弹相对运动学方程;第2节分别针对静止点与面目标设计了2种与1种协同制导方法;第3节通过仿真对所设计的协同制导方法进行研究分析;第4节进行了总结。
1 从弹运动方程组建立
考虑在集中式“领弹-从弹”协同制导架构下,在平面内有n枚装备有双捷联探测器的无导引头也无惯导的导弹Mi(i=1,2,…,n)作为从弹,在一枚有导引头且弹身安装有两个靶点的导弹Ml的带领下,对静止目标T进行攻击。为了简化相应算法的设计过程,基于理想情况提出以下假设:① 导弹的速度大小恒定;② 不考虑飞行中的重力影响与外在干扰;③ 导弹的攻角或侧滑角足够小。假设①与②在制导律设计中经常被采纳[19],而假设③也常出现在考虑导引头视场角约束的制导律设计中[20-22]。由于导弹速度大小恒定,故合理假设从弹可预先得到领弹以及其自身的速度大小。
由于导弹升力可由攻角与舵偏角近似线性表示,故基于假设②与③可知在铅垂面内导弹法向加速度可仅由舵偏角线性表示。因此,虽然从弹不存在惯导,但仍能通过调节舵偏角实现特定的法向加速度指令。由于从弹不具有导引头与惯导,故只能测得两组探测器相对于领弹弹身上特定靶点的视线距离(rC与rD)以及此视线相对于从弹弹体纵轴的夹角。由于rC与rD数值往往较小,故探测器的测量误差对于从弹脱靶量的影响较小。基于假设③可知,上述由捷联探测器测得的角度等价于从弹速度方向相对于探测器视线的前置角ηC与ηD。因此,本文的研究目是为从弹设计制导律使其可基于探测器的上述测量值实现对目标的精确打击。
假设在中制导段结束时可实现领弹与从弹的相对位置满足探测器的测量要求,如图1所示。其中,探测器与靶点均沿导弹纵轴方向安装;下标i与l分别表示从弹i与领弹;C/D与A/B分别代表从弹弹体上的两个探测器与领弹弹体上对应靶点位置;ϑ与d分别表示弹体姿态角与两探测器(或靶点)间距。
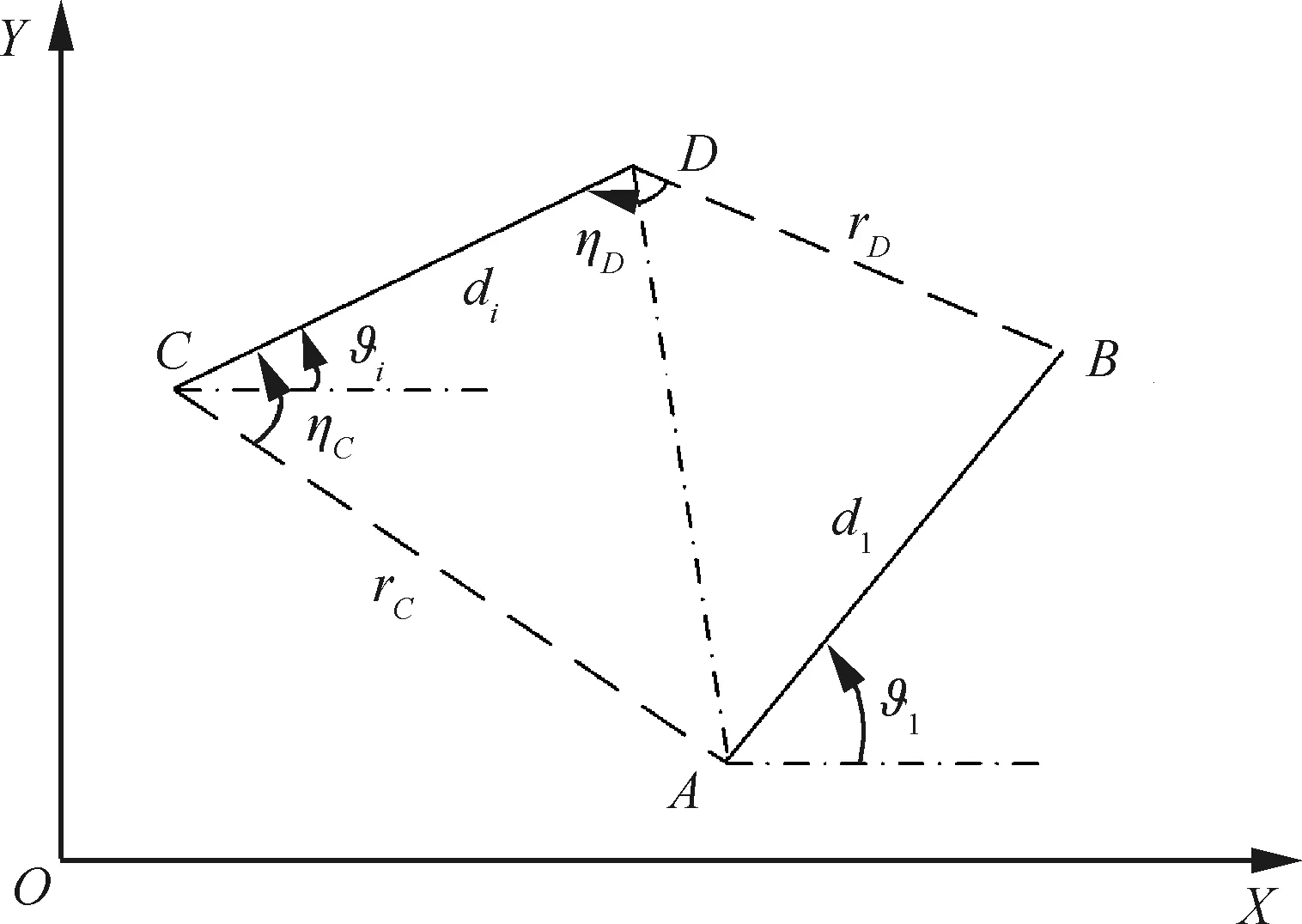
图1 领弹与从弹的相对位置
定理1从弹通过探测器的测量值可得到其与领弹的姿态角之差,即ϑl-ϑi。
证明:基于图1可知,dl与di在安装探测器与靶点时已知,而两点间距|AC|,|BD|与角度∠ACD(即rC,rD与ηC),从弹可通过探测器测量得到。因此,对于三角形△ACD,|AD|可由余弦定理得到
(1)
对于△ACD与△ABD,∠CAD与∠BAD可分别采用正弦与余弦定理得到
(2)
(3)
由于领弹与从弹的姿态角之差为
ϑi-ϑl=∠ACD-(π-∠BAD-∠CAD)
(4)
故将式(1)~式(3)代入式(4),可得
ϑl-ϑi=π-
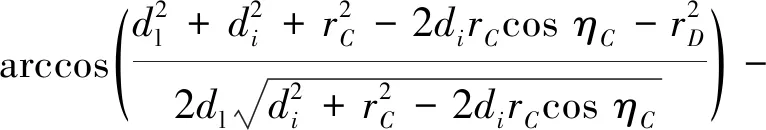
(5)
由于式(5)中的dl、di、rC、rD与ηC均可测得,故可证明领弹与从弹的姿态角之差可通过探测器的测量值求解得到,即定理1得证。
为了便于协同制导律的设计,假设点A与C分别表示领弹与从弹的质心,故可得到领弹与从弹的质点运动状态如图2所示。其中,带有下标li的状态量表示从弹相对于领弹的运动状态,而rli与ηli等价于rC与ηC。
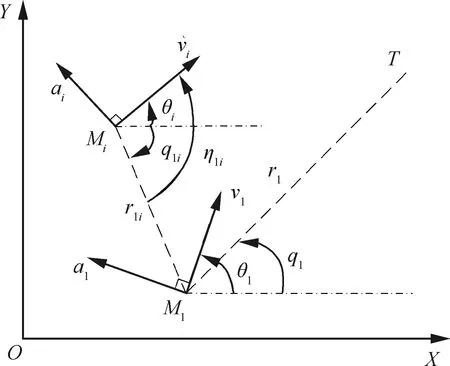
图2 领弹、从弹与目标的质点运动模型
在图2中,v、a、θ与q分别表示速度、法向过载、弹道角与视线角。
(6)
ηli=θi-qli
(7)
由此,可建立从弹相对于领弹的运动学方程为
(8)
(9)
领弹与从弹的弹道角之差(Δθ)可表示为
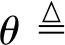
(10)
而基于假设③可知,Δθ等于由定理1得到的领弹与从弹的姿态角之差,即
Δθ=ϑl-ϑi
(11)
将式(7)与式(10)代入式(8)与式(9)中,可得
(12)
(13)
由式(7)可知
(14)
故将式(6)与式(13)代入式(14)中,可得
(15)
综上,可得到推导从弹制导律所需的质点运动学方程(式(12)与式(15)),而方程中的全部变量均可由从弹测量得到。
2 从弹的末制导律设计
2.1 针对点目标的协同制导律
装备有导引头的领弹可通过一般制导律实现对目标的精确打击,而在领弹命中目标后,从弹的探测器将失去作用,故在设计从弹的制导律时需要根据领弹是否已命中目标分成两段考虑[17]。显然,若在领弹命中目标时,从弹相对于领弹的前置角ηli为0,则从弹之后只要作直线运动即可保证命中目标。因此,为保证从弹的前置角在领弹命中目标前趋于0,可设计其制导律为
ai=-vi(k1ηli+k2Δθ)
(16)
式中:k1与k2均为正常数。

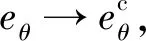
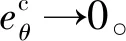
显然,ηli在领弹命中目标前的收敛精度决定从弹的脱靶量。对于式(16)设计的制导方法,虽然通过选择较大的制导参数可提高ηli的收敛精度,但势必会增大从弹的最大所需过载。由于采用有限时间收敛可提高收敛精度[19],故本文进一步设计了一种可实现ηli在有限时间内收敛的制导方法,即

(17)
式中:k3为正常数;指数μ满足:μ∈(0,1);sign(·)为符号函数。
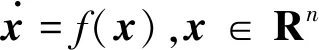
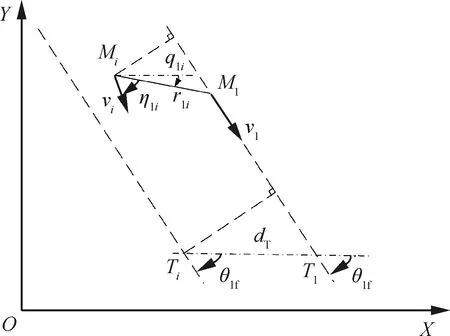
定理2基于式(17)设计的制导方法可实现ηli在有限时间内收敛。
证明:将式(17)代入式(15)中可得
(18)
定义连续的正定函数Z为
(19)
对式(19)求导可得
(20)
将式(18)代入式(20)中,可得
(21)
考虑到
(22)
因此
(23)
将式(19)代入式(23)中,可得
(24)
由于μ∈(0,1),故(μ+1)/2∈(0,1)。因此,基于引理1可知ηli将在有限时间内收敛于0。
评论1若领弹采用比例导引,可得到其攻击时间为[24]
(25)
式中:Nl为导航比;在本文中下标0均表示末制导的初始时刻。因此,对于有限时间制导律,为了保证ηli在领弹命中目标前趋于0,基于引理1可知制导系数需满足:
(26)
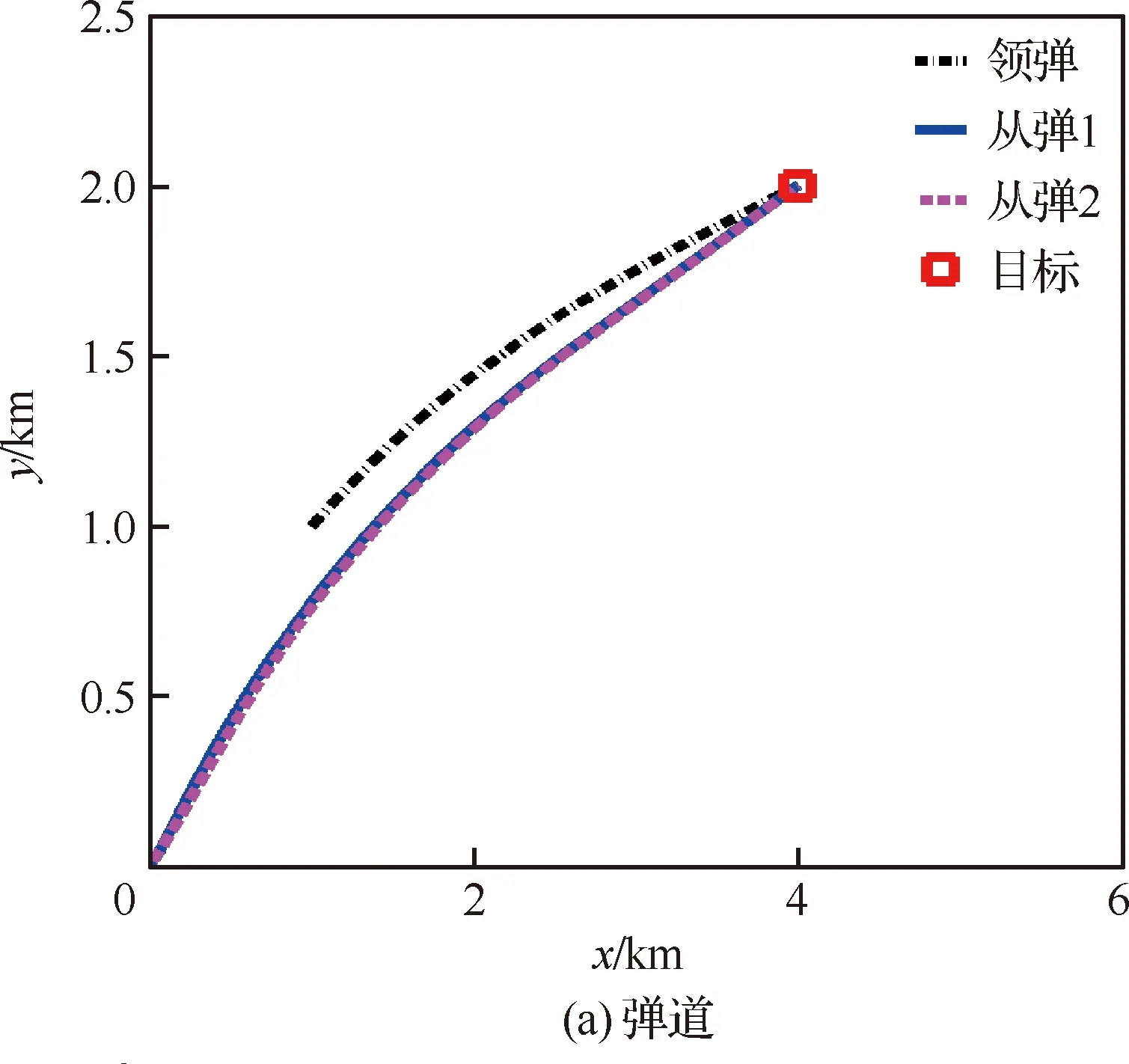
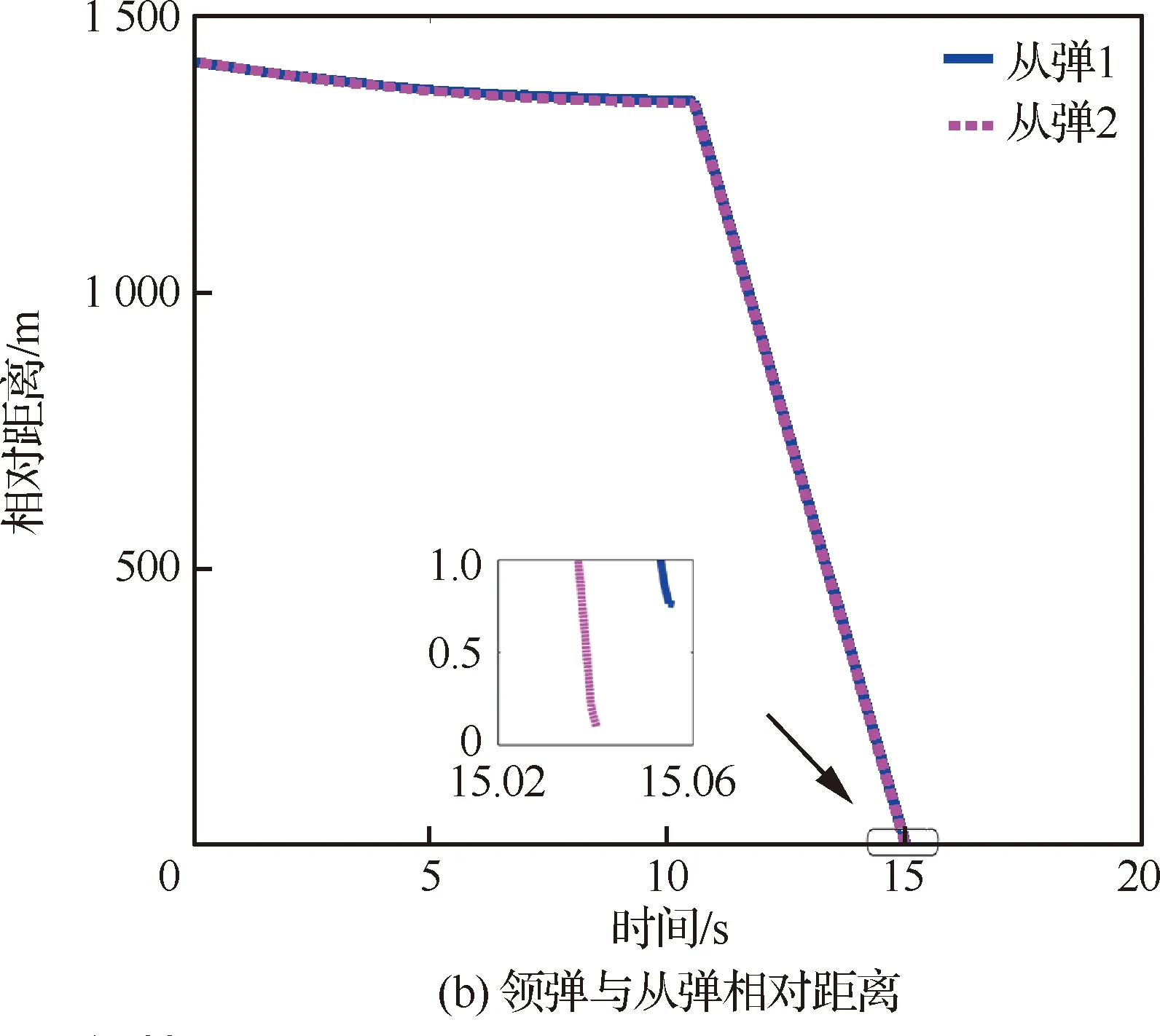
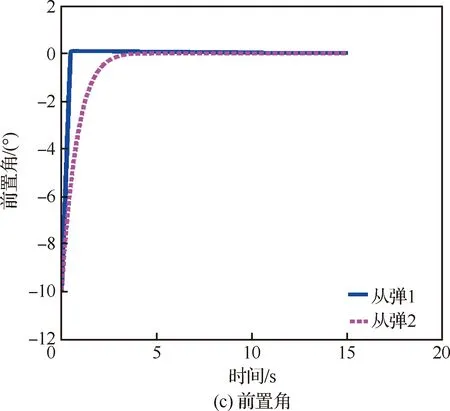
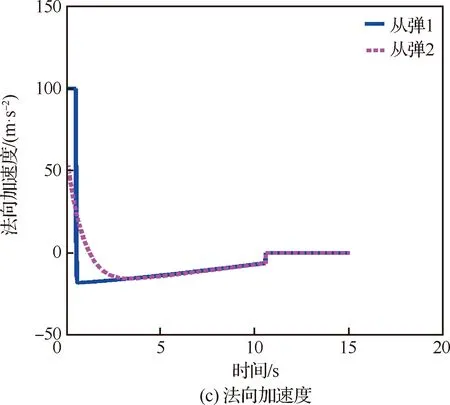
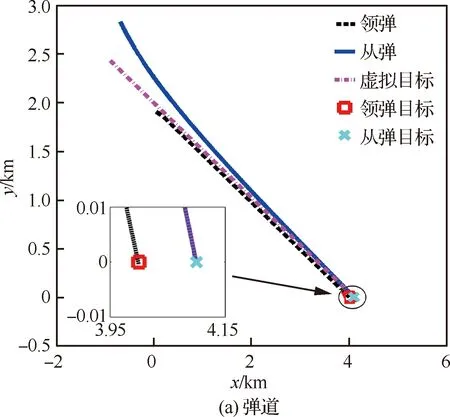
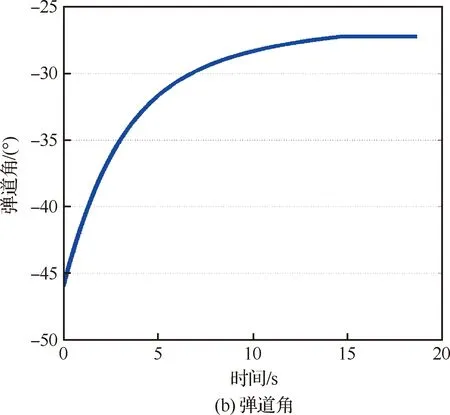
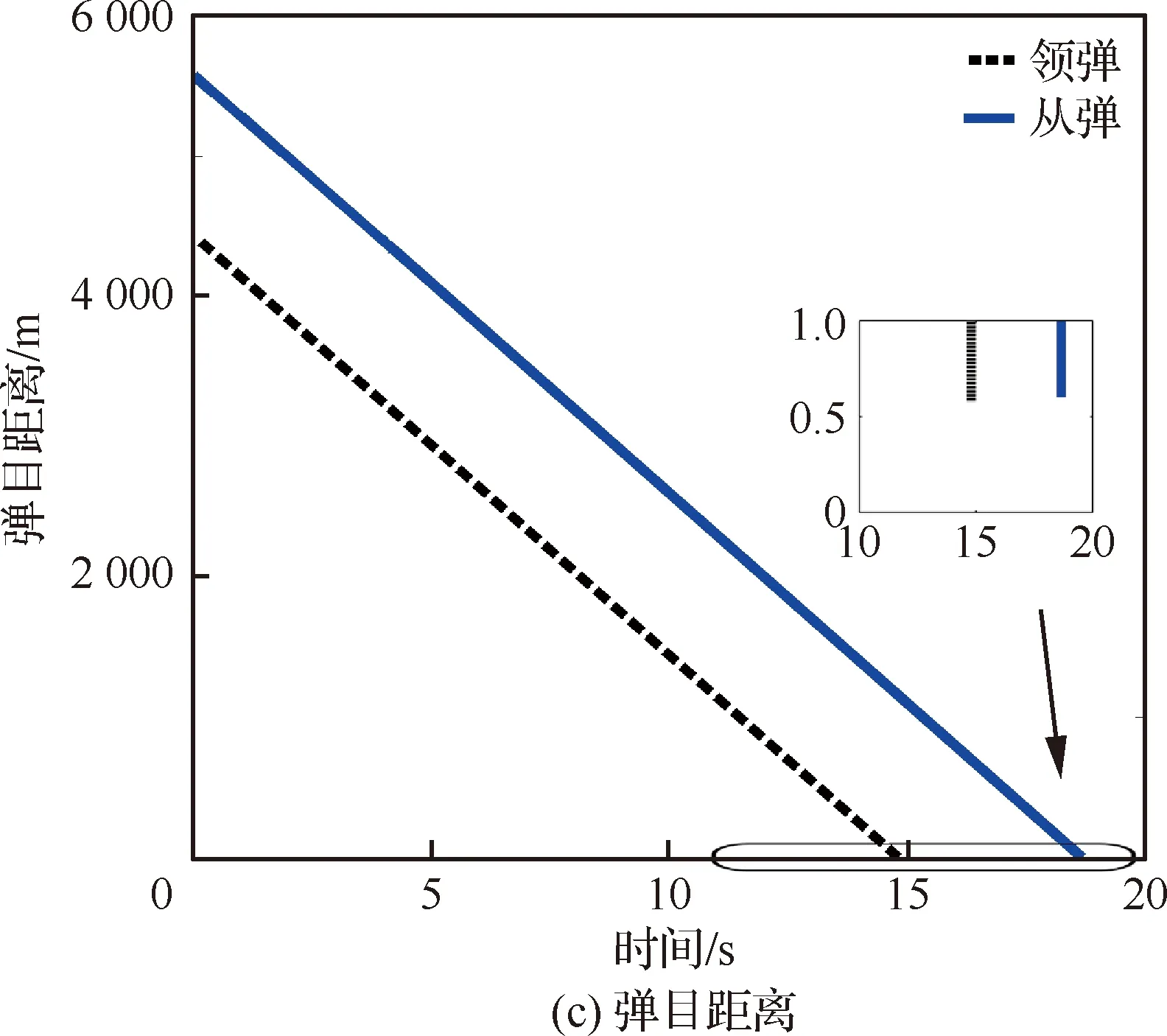
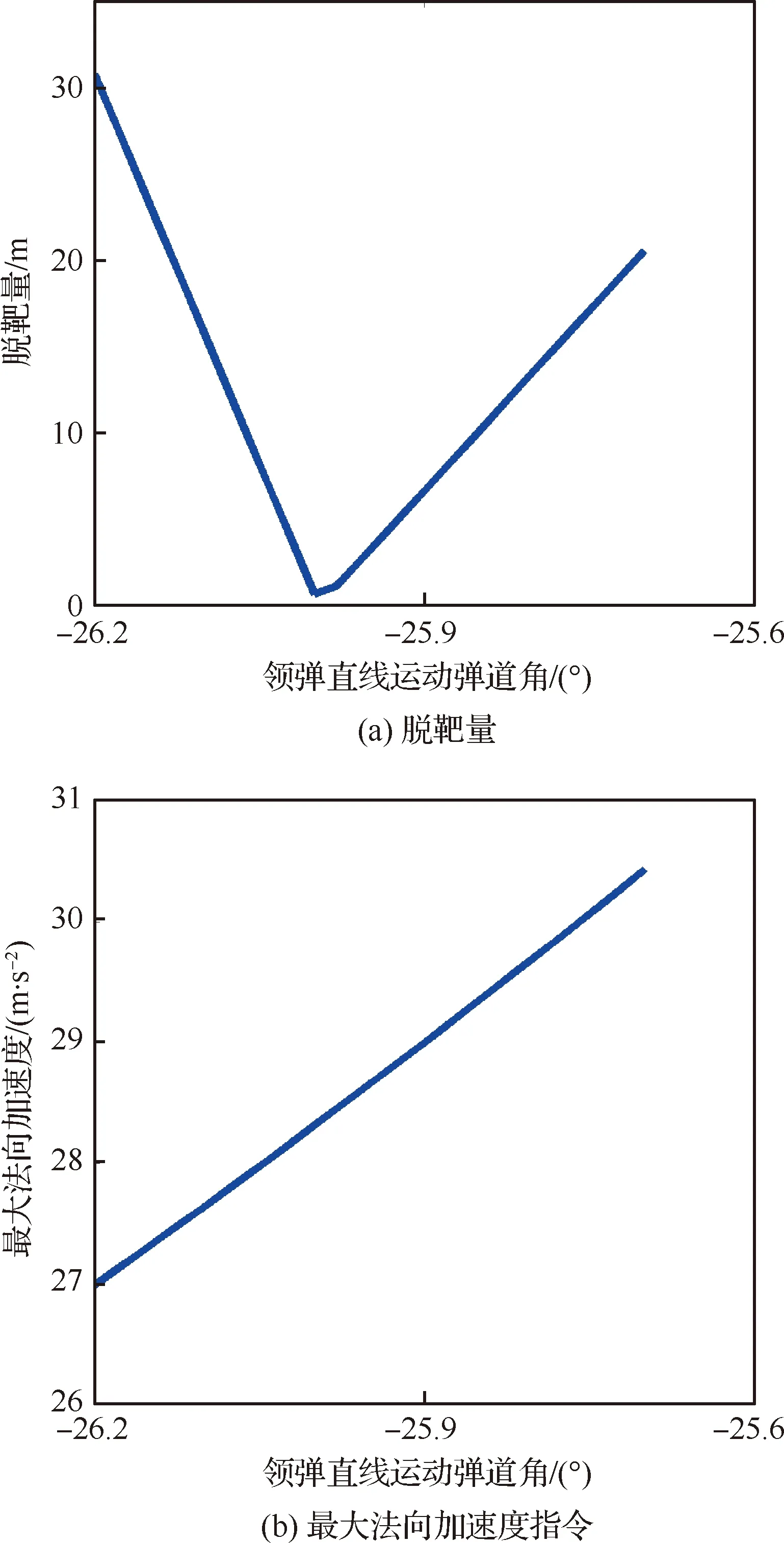
由于对于机动目标的末制导往往会变成尾追模式,故领弹与从弹的弹道角之差(Δθ)可认为将近似收敛于0且足够小。因此,若在领弹命中目标前满足vi rli0≥tlf(vi-vl) (27) 此外,考虑到探测器的“锁定”距离有限,rli0的上限可表示为 (28) 式中:ld为探测器的“锁定”距离。此外,由于探测器的测量角度ηli将收敛于0,故只要初始时刻的ηli0满足对探测器的测量角度约束即可。 对于静止面目标,要求导弹集群对目标进行散布攻击,即在面目标上领弹(Tl)与从弹(Ti)的目标点存在一定间距(dT),如图3所示。领弹采用文献[25]设计的圆弧-直线制导律,可很快实现弹道角为固定值θlf的直线运动: 图3 领弹、从弹与目标的相对运动 (29) 式中: (30) 式中:Δ1=sin(θl0-θlf)sin(ql0-θlf);Δ2=cos(ql0-θlf)-cos(θl0-ql0)。 在图3中,过从弹目标点Ti并以倾斜角θlf为从弹设计虚拟线目标。若从弹的位置与速度方向在领弹命中目标前均收敛于虚拟线目标,则在此之后从弹只要作直线运动即可命中Ti。为了实现从弹的位置与速度方向均收敛于虚拟线目标,可设计从弹的制导律使得位置(er)与弹道角(eθ)误差均收敛。其中,位置与弹道角误差由图3所示的几何关系可被分别定义为 (31) eθ=Δθ (32) 将式(7)与式(10)代入式(31)中,可得 er=rlisin(Δθ+ηli)+dTsinθlf (33) 分别对式(32)与式(33)求导,可得 (34) (35) 由于对于机动领弹,从弹往往采用尾追的方式进行跟踪,故可假设ηli足够小。此外,由于Δθ可被认为足够小,故对式(35)线性化后可得 (36) 将式(32)代入式(36)中可得 (37) 为了保证er收敛,不妨假设: (38) 式中:kr为正常数。 接着,将式(38)代入式(37)中可得到为保证er收敛所需的eθ,即 (39) 对式(39)求导后可得 (40) ξ=visinηli-vlsin(Δθ+ηli) (41) ζ=vicosηli-vlcos(Δθ+ηli) (42) 将式(41)与式(42)分别代入式(15)与式(12)中,可得 (43) (44) 对式(12)与式(15)分别求导后可得 (45) (46) 将式(45)与式(46)进行变换后可得 (47) (48) 将式(6)、式(41)与式(43)代入式(47),经过化简可得 (49) 将式(6),式(41)~式(43)代入式(48)后经过化简可得 (50) 基于式(6)与式(43)可得 (51) 将式(38)、式(43)、式(44)与式(49)~式(51)代入式(40),经过化简可得 (52) 将式(44)与式(51)代入式(39)中,可得 (53) (54) 式中:kθ为正整数。将式(32)、式(34)、式(52)与式(53)代入式(54)中可得到从弹的法向加速度指令为 ai= (55) 将式(12)与式(15)代入式(39)中,可得 (56) 将式(56)线性化后可得 (57) 基于Δθ与ηli的小角度假设,式(57)可被化简为 (58) 在仿真中,一枚无导引头也无惯导的从弹在一枚有导引头领弹的带领下对目标进行打击,其中领弹采用比例导引。考虑到导弹的毁伤范围、机动能力,以及探测器的“锁定”距离有限,仿真时要求导弹脱靶量小于1 m,法向加速度指令小于100 m/s2,以及领弹与从弹的相对距离小于1 500 m。 首先,假设静止点目标位于(4 000 m,2 000 m)处,领弹与从弹的初始运动状态如表1所示。其中,从弹1与从弹2表示具有相同的初始运动状态,且分别采用式(16)与式(17)的制导方法的两枚从弹。通过引入饱和函数使得两枚从弹的法向加速度指令满足约束。仿真结果如图4所示。 图4(a)为导弹的弹道。由此可知,领弹与两枚从弹均可命中目标。领弹与从弹的相对距离(在领弹命中目标后表示弹目距离)如图4(b)所示,其中从弹1与2的脱靶量分别为0.76 m与0.10 m,均满足对导弹脱靶量的要求。此外,由此图可知,领弹与从弹的相对距离也均满足要求,且领弹与从弹在领弹命中目标前均不会发生碰撞。图4(c)为两枚从弹的前置角,表明这两个角度在领弹命中目标前均可收敛于0,由此验证了所设计的2种协同制导律的有效性。图4(d)为两枚从弹的法向加速度指令,表明两者的最大值在饱和函数的作用下均可满足要求,但从弹2的最大法向加速度只有从弹1的一半左右。这是因为对于式(16)设计的制导方法,为了提高从弹前置角在领弹命中目标前的收敛精度以满足脱靶量约束,需要选取更大的制导参数,但这显然会增大最大法向加速度指令。通过上述对两枚从弹的仿真结果对比可知,式(17)设计的制导方法相比于式(16)的可同时实现更小的脱靶量以及最大法向加速度,但过载表达式较复杂,即意味着对弹载计算机的计算性能提出了更高的要求。 对于静止面目标,导弹的初始运动状态如表2所示。在仿真中,选择领弹与从弹的目标位置分别为(4 000 m,0 m)与(4 100 m,0 m),即两目标的间距dT=100 m,且领弹在直线运动阶段的弹道角θlf=-26°,则仿真结果如图5所示。 表1 针对点目标导弹的初始运动状态 图4 针对点目标的仿真结果 表2 针对面目标导弹的初始运动状态 图5(a)为导弹的弹道。由此可知,领弹与从弹均可命中各自的目标点。图5(b)为从弹的弹道角。结合图5(a)与图5(b)可知,从弹的位置与速度方向均可在领弹命中目标前近似收敛于虚拟线目标。图5(c)为导弹与目标的距离随时间变化的曲线。由此可知,领弹与从弹的脱靶量分别为0.58 m与0.60 m,均满足对导弹脱靶量的要求。图5(d)与图5(e)分别为领弹与从弹在领弹命中目标前的相对距离以及两枚导弹在制导全过程的法向加速度指令,从而验证了两枚导弹的相对距离以及最大法向加速度均满足要求。由上述仿真结果可知,无导引头也无惯导的从弹可在有导引头领弹的带领下实现对静止面目标的精确打击。 图5 针对面目标的仿真结果 图6为选择不同的θlf对从弹制导性能(脱靶量与最大法向加速度指令)的影响。由此可知,在一定范围内增大θlf,则从弹的脱靶量先减小再增大,而最大法向加速度指令则持续增大。 图6 θlf对于从弹制导性能的影响 1) 利用从弹双探测器的测量值设计了一种可得到领弹与从弹的弹道角之差的计算方法。 2) 建立了以探测器的测量量为状态变量的导弹相对运动学方程,并在此基础上采用集中式“领弹-从弹”协同制导架构,分别针对静止点或面目标为从弹设计了2种与1种末制导律,实现了无导引头也无惯导的从弹在导弹间不实时通信以及不需要导弹绝对位置信息的情况下对目标的精确打击。 3) 通过仿真验证了所提出的3种制导律的有效性,并通过分析比较给出了针对点目标设计的2种制导律的优缺点。2.2 针对面目标的协同制导律

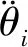
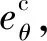
3 仿真与分析




4 结 论
