一种适用于曲面结构的机器人制孔误差在线补偿技术
2019-10-31王龙飞张丽艳叶南
王龙飞,张丽艳,叶南
南京航空航天大学 机电学院,南京 210016
飞机零部件装配是飞机产品生产中非常重要的一个环节,随着对生产效率和质量要求的不断提高,采用工业机器人进行飞机零部件自动制孔的方法正在不断推广。采用机器人进行自动制孔时通常存在机器人绝对定位误差、零部件与机器人位置关系找正误差、零部件外形误差等因素,各种误差累积会影响制孔精度。因此,补偿综合误差以提升机器人在零部件表面的定位精度是机器人自动制孔技术的一个重要前提。
国外对机器人自动制孔的研究起步较早,许多研究成果已在生产中投入使用[1],如波音、空客等部分飞机机翼、襟翼等已采用机器人自动制孔技术[2-3];Devlieg和Szallay[4]提出在机器人各轴上集成编码器进行轴位置反馈,通过优化运动模型并最终形成一个高精度的运动平台,其精度提升效果通过机器人在上下表面分别制孔得到了验证。国内学者针对机器人自动制孔技术也进行了大量的研究。朱伟东等[5]通过分析冗余度,提出了一种利用参照孔进行线性或双线性插值的补偿方法,但该方法更适用于外形较为平坦的零部件;董辉跃等[6]从线性插值出发,通过分析误差来源和曲面构造原理,提出了构造误差Coons曲面进行曲面插值的补偿方法,该方法针对不同外形工件需要进行不同的误差曲面函数构造,计算量大且较为复杂;田威等[7-8]基于空间误差相似性提出了反距离加权和关节空间误差建模的离线补偿方法,但该方法难以补偿自动制孔中的除机器人自身定位误差外的其他误差。基于视觉反馈的机器人制孔误差补偿方法中,高效率和高精度的手-眼关系标定是非常重要的一步。Zhan 和 Wang[9]等提出在场景坐标系下计算刀具中心点与相机图像的转换关系间接完成手眼标定的方法,但该标定方法的完成需要驱动机器人带动刀具中心点移动且仅适用于平坦结构制孔;朱伟东等[10-11]提出了一种通过计算标定板圆孔实际尺寸与图像中像素尺寸线性关系及图像中圆孔的整体偏转角等,以同时完成相机内参计算和手-眼关系建立的方法,该标定方法在一定程度上降低了标定计算的复杂度,但相机实际测量时孔位并非刀轴直接对准的位置,测量后还需根据相机与刀具之间位置关系移动机器人位置。文献[12-14]利用激光跟踪仪建立各坐标之间位置关系,并通过激光跟踪仪实时监测机器人末端位姿,修正末端姿态,以提升制孔精度,但这种方法相比于在线视觉反馈方法而言集成度和自动化程度较低。此外,孔位垂直度也是衡量制孔质量的一个重要标准,文献[15]采用压脚进行钻孔法向测量,但接触式测量存在损伤工件表面的可能;文献[16-17]中采用激光传感器反馈方法对待钻孔局部法向进行修正,有效地提升了制孔垂直度,但制孔垂直度需要预先定位到精确的制孔位置,从而在待钻位置局部进行法向修正,因此准确地定位待钻孔位置是自动制孔的前提。
针对机器人自动制孔过程中的定位误差在线补偿问题,本文提出以固联于机器人末端的相机成像平面和制孔工作平面之间的单应关系作为手-眼关系进行标定;在实际制孔过程中,机器人带动相机及激光测距传感器依次在确定的工作高度对基准孔进行拍摄,通过标定出的手-眼单应关系对基准孔孔心相对于刀具的三维偏差进行测量,并反馈驱动机器人进行末端姿态调整,直至到达基准孔上方理想位置,根据一组基准孔对应的机器人理论驱动坐标及实际驱动坐标(机器人驱动坐标即机器人要达到某一位置时所需要的坐标,等同于机器人示教器中的读数)计算出基准孔对应的机器人驱动坐标三维误差变换矩阵,据此获得这组基准孔邻域范围内各待钻孔的机器人驱动坐标补偿量,从而实现待钻孔制孔位置误差补偿。该方法易于实现,且适用于曲面结构上的孔位误差补偿。
1 坐标系关系建立
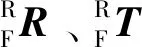
法兰坐标系OF和工作平面坐标系OP的z轴方向相同,且均与刀具轴线(即刀具坐标系z轴)重合,刀具坐标系OT原点与工作平面坐标系OP的原点重合,取在刀尖点下一定的安全距离处,以免机器人到达指定位置拍照时发生刀具与工件碰撞,OP坐标系的xy平面本文称为制孔工作平面(机器人按照刀具坐标系到达指定位置时,制孔工作面与指定位置的局部平面重合);相机坐标系记为OC;激光测距传感器通常安装3~4个传感器在刀具周围,共同确定测距传感器坐标系OS;坐标系OM是用于自动制孔之前建立各坐标系关系的外部测量系统坐标系。本文所有坐标及向量均为列向量。
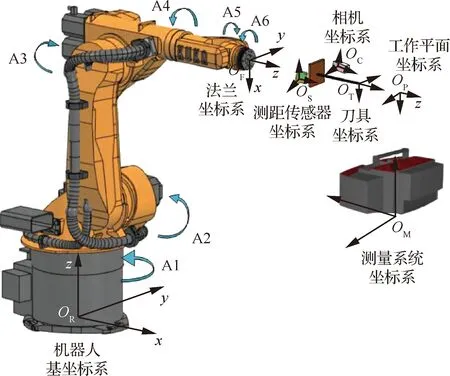
图1 各坐标系关系
1.1 机器人基坐标系和法兰坐标系的建立
由本文所使用的6自由度串联工业机器人设计特点可知,其基坐标系OR的x轴和z轴分别与其A6轴和A1轴的轴线平行,因此可通过测量设备,测量分别转动A6轴和A1轴时法兰盘上标记点在测量系统坐标系OM下的位置变动,通过拟合标记点的圆形运动轨迹,获得坐标系OR的x和z轴在测量系统坐标系OM下的位置[18]。
设在OM坐标系下OR坐标系的x轴、z轴分别为MxR、MzR,则OM坐标系下OR坐标系的y轴可表示为
MyR=MzR×MxR
机器人基坐标系OR向测量坐标系OM变换的旋转矩阵则为
(1)
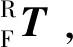
(2)
通过OR坐标系与OM坐标系之间的变换关系式(1)和式(2)可将后续外部测量设备测量到的坐标转换至OR坐标系下。
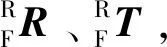
1.2 其他坐标系的建立
法兰盘在制孔工作中起到固连刀具及测量反馈装置的作用。本节在1.1节的基础上阐述建立坐标系OS、OC、OT及OP之间相互关系的方法。图2所示为系统中各组件位置示意。
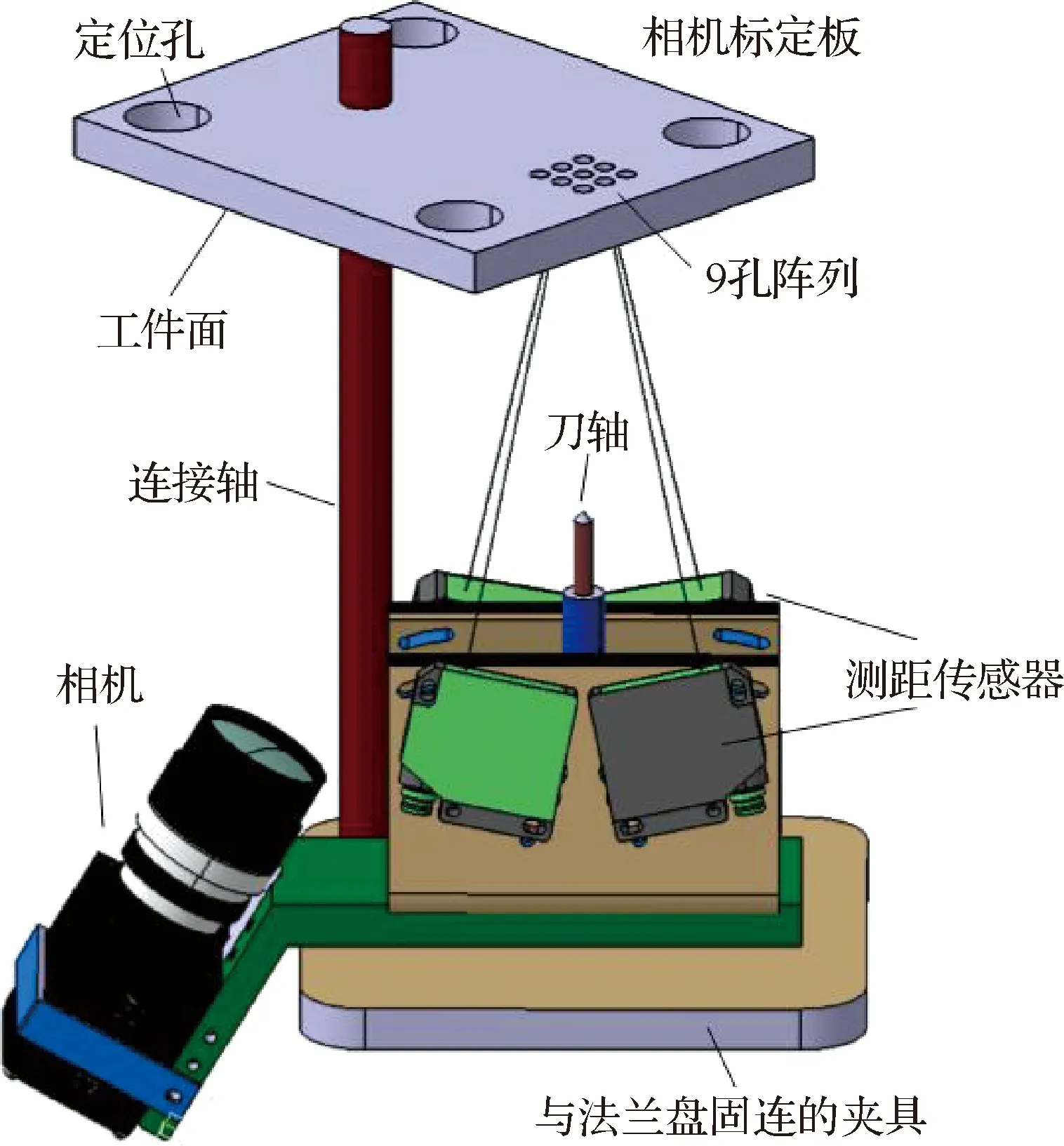
图2 其他坐标系位置关系
为了建立工作平面坐标系,进而建立以像平面与制孔工作面之间单应关系所表达的机器人制孔系统手-眼关系,本文采用一块特制标定板(参照文献[10]),由4个定位孔、一个9孔阵列以及1个连接轴安装孔组成。本文进行相机标定时,机器人处于HOME位置,标定板通过一根刚性连接轴安装在法兰盘末端,连接轴平行于刀具安装在夹具上,安装后标定板工作面与法兰盘平面平行(机加工可保证工作面与法兰盘的平行度误差远小于制孔位置误差要求),距离法兰坐标系xy平面的距离为h(由刀具的长度及预留的制孔安全距离等决定);法兰坐标系OF的z轴穿过9孔阵列区域,其与9孔阵列交点记为工作平面坐标系OP原点;相机倾斜安装在夹具侧边,与标定板之间的相对位置由倾斜角度和相机物距等决定,安装好能清楚拍摄到9孔阵列位于图像中心区域;刀具坐标系OT位置由测量系统获得;激光测距传感器在本文方法中一方面辅助相机进行位置测量,另一方面可对制孔法向进行测量调整。激光测距传感器和相机固连于法兰盘上,连接轴和标定板均可拆卸。
目前的常见的机器人在线定位误差补偿方法中,相机通常是平行于刀轴安装,这种方法需要相机正对于孔位上方拍摄,本文的相机安装方式,可保证刀具坐标系原点位于图像中心区域,进行实际制孔工作时,机器人带动刀具到达指定位置后即可直接采用相机进行孔位位置测量,这样测量后无需再次根据相机与刀具之间关系移动机器人,可直接进行制孔工作,实时性更高。
1.2.1 激光测距传感器坐标系建立
激光测距传感器坐标系OS与法兰坐标系OF的关系建立有平面标定法和球面标定法[19],两种标定方法又可分别分为:机器人静止、面移动和机器人移动、面静止两种标定方式。采用机器人移动、面静止的方式进行传感器手眼标定时,由于机器人运动误差的存在,需要精确测量机器人法兰坐标系的实时位姿,过程较为繁琐;采用机器人静止,面移动的方式时,实时测量球面的位置较为困难,因此本文采用平面标定法,以机器人不动,调整并实时测量平面位置的方式对激光测距传感器进行手眼关系标定。以其中一个传感器为例,具体为:
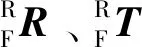
Π:Ax+By+Cz+D=0
(3)
同时测量传感器的测量距离,记为ds。
2) 改变平面Π的位姿,重复1),直至测量次数n≥6。
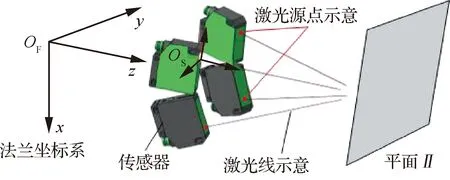
图3 传感器坐标系建立
获得OF坐标系下n个平面Πi(i=1:n)方程和对应测量距离dsi(i=1:n)。则传感器在OF坐标系下的坐标原点(xs,ys,zs)和方向(nx,ny,nz)满足
(4)
1.2.2 工作平面坐标系建立
首先将机器人置于HOME位置,然后通过外部测量系统获得OF坐标系原点距标定板工作面的距离h(即OP与OF坐标系原点之间的距离),以及标定板工作面上4个定位孔孔心在OM坐标系下的位置坐标,记为MpL,i(i=1:4)。则4个定位孔在机器人基坐标系下的坐标RpL,i(i=1:4)为
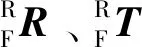
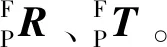
1.2.3 手-眼关系建立
采用视觉反馈方法时,高效且精确的手-眼标定是关键一步。本文提出一种基于单目视觉图像与制孔工作面之间单应变换的手-眼关系表征和标定方法。
记机器人处于HOME位置时相机拍摄到的9孔阵列第i个孔的孔心在图像中的坐标为(ui,vi)(i=1:9)。标定板上9孔阵列与4个定位孔相对位置已知,记OP坐标系下9孔阵列坐标为PpN,i(i=1:9),下标N表示9孔阵列,则9孔阵列在OF坐标系下的位置FpN,i(i=1:9)为
需要指出的是,通过计算OF坐标系下9孔阵列的z坐标值的平均值可获得h的计算值,通过与h的测量值进行比较,可计算坐标转换偏差;此外计算9孔阵列的z坐标值的波动范围可获得标定板工作面与法兰盘的平行度误差情况。由于本文手眼标定方法均在机器人HOME位置下进行,标定板与刚性连接轴仅在相机标定时安装,且标定耗时短,因此连接轴挠曲变形对法兰盘和标定板之间平行度的影响可忽略,相关实验结果将包含在本文第3.1节。
完成9孔阵列在OF坐标系下的坐标转换之后,利用9孔中心坐标的x、y坐标值与相机标定图像中对应的9孔阵列的坐标(ui,vi)(i=1:9)进行标定板平面与相机成像平面之间映射关系f的计算。
理论上f应包含笛卡尔坐标到图像坐标之间的线性映射关系和由于成像系统畸变引起的非线性映射关系,但由于标定时9孔阵列位于标定图像中心区域,且实际制孔中的基准孔尺寸较小,映射关系f中的非线性畸变可以忽略(详细实验验证方法及实验数据见第3.1节)。因此,本文将f简化为工作平面与相机图像之间的线性单应关系H,H为3×3矩阵,且满足
(5)
式中:FpN,i(x)、FpN,i(y)分别表示OF坐标系下9孔阵列第i(i=1:9)个孔的x、y坐标值。将9孔中心坐标在OF坐标系下的x、y坐标值与相机标定图像中对应的9孔阵列的坐标(ui,vi)(i=1:9)代入式(5)即可获得单应关系H。图4为上述映射关系建立的基本流程。
在机器人实际制孔定位工作时,只要保证每次相机拍摄高度与标定时的拍摄高度一致、基准孔平面相对于法兰盘的位置与标定时工作面相对于法兰盘的位置相同,则根据标定板平面建立的映射关系f(即单应矩阵H)就可以用于表达基准孔平面与相机成像平面之间的映射关系。由第1节可知,刀具坐标系OT与工作平面坐标系OP的原点及z轴均重合,因此单应矩阵H即可表示相机与刀具坐标系xy平面之间的映射关系。本文以单应矩阵作为手眼关系,可省略相机内参求解,此外单应方法不需要像平面与待拍摄平面平行,相机以倾斜角度安装更具灵活性。
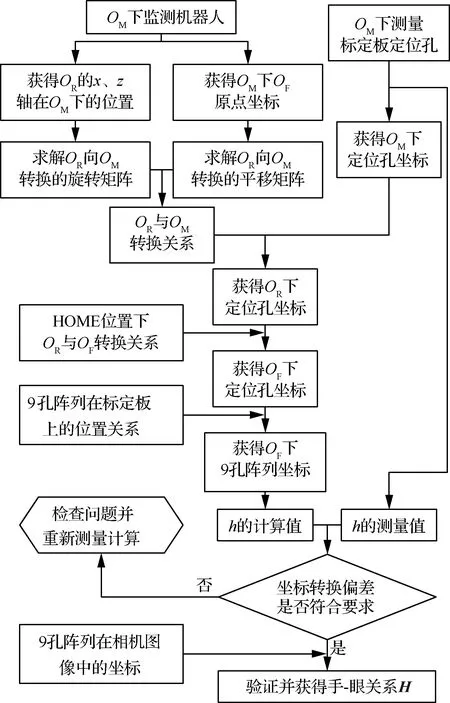
图4 手-眼关系建立流程
2 孔位误差补偿
机器人进行制孔工作之前,需要进行零部件找正,即通过外部测量方法找到零部件相对于机器人基坐标系的位置,从而将工件坐标系下的所有理论孔位(包括基准孔和待钻孔)的坐标值和孔方向向量转换到机器人基坐标系OR下。本节阐述工件找正后孔位误差的在线补偿方法。
2.1 基准孔欧拉角计算
设零部件上的1个基准孔在OR坐标下的理论坐标为Rpt,孔方向垂直于零部件表面向内,记为Rvt,要使机器人带着刀具沿孔方向运动至基准孔正上方需要计算法兰盘末端欧拉角,欧拉角值的确定由旋转矩阵变换得到。对零部件上每个基准孔所对应的欧拉角本文通过预先设定孔心坐标系OH来求解。
图5所示为孔心坐标系OH示意图,红色圆点表示孔心,红色射线表示孔方向的单位向量,蓝色射线表示与孔方向正交的两个单位向量。
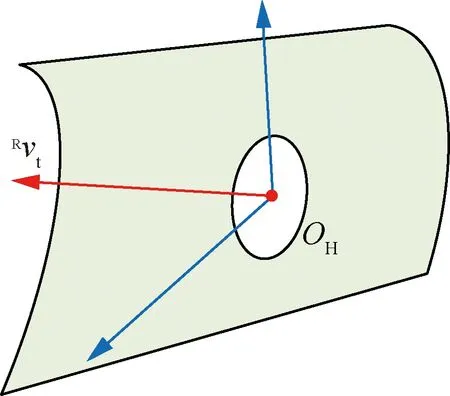
图5 孔心坐标系
设孔方向为孔心坐标系OH的z轴,记z轴为
z,有
z=Rvt
(6)
设对应的OH坐标系的x轴为x,本文方法中机器人到达指定位置时法兰坐标系OF无特殊方向要求,故本文取
(7)
式中:z(1)和z(2)分别表示z的第1和第2个坐标值。则OH坐标系的y轴y为
y=z×x
(8)
孔心坐标系OH在OR坐标系下的旋转矩阵R可表示为
(9)
此时坐标系OF、OT与OH方向相同,因此旋转矩阵R也是OF和OT向OR变换的矩阵。通过旋转矩阵与欧拉角的转换[20]可求出机器人运动至指定孔位时所对应的法兰盘末端的欧拉角。
2.2 基准孔的机器人驱动误差计算
由第1节可知,OP坐标系与OF坐标系z轴方向相同,因此,当不存在零部件找正误差及机器人定位误差等因素时,通过基准孔对应的机器人驱动坐标(即基准孔理论坐标)按孔心坐标系的定义规则式(6)~式(9)求解出的欧拉角,使机器人移动至某个基准孔上方h距离后,OP与OH两坐标系的原点及z轴重合,即孔心位于制孔工作平面上,并且机器人自身运动可保证OF坐标系与OH坐标系方向相同,如图6中理论姿态(红色坐标系)所示。但由于工件找正误差、机器人运动误差等因素存在,工件的实际位置与机器人按基准孔理论驱动坐标到达的实际位置如图6中实际姿态(蓝色坐标系)所示。
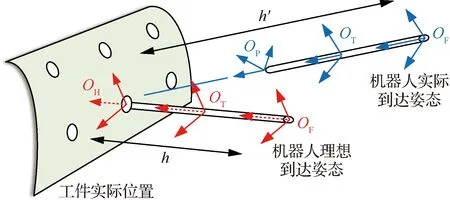
图6 机器人制孔状态示意图
定义基准孔的机器人驱动误差为
e=Rdp-Rdt
(10)
式中:误差值e=|e|;Rdp、Rdt分别表示机器人理论驱动坐标和实际驱动坐标。易知Rdt满足
Rdt=Rpt
(11)
通过标定后的相机及激光测距传感器测量反馈,可驱动机器人进行姿态变动,直至到达精度控制范围内的理想姿态(本文以传感器测量获得的局部法向与刀轴偏差角θ<0.35°、圆孔局部平面距OF坐标系的距离h′与坐标系OF和OP之间距离h偏差eh=h′-h<0.5 mm且相机测量到的圆孔中心点在OF坐标系xy平面上的偏差e2D<0.2 mm时认为到达理论姿态。为方便说明,本文称e2D为相机检测偏差)。具体姿态调整步骤为(前三步顺序可调换):
1) 利用激光测距传感器测量刀具轴线与基准孔平面法线的夹角,根据夹角的测量反馈进行机器人末端姿态调整,直至基准孔局部平面法向与刀具轴线之间的偏角达到精度控制范围内。
2) 利用激光测距传感器测量基准孔局部平面至法兰盘坐标系xy平面的距离h′,根据距离的测量反馈进行机器人末端相对于基准孔局部平面的高度调整,直至h′与h的偏差值达到精度控制范围内。
3) 根据相机检测偏差反馈进行机器人末端位置调整,直至刀具轴线与基准孔平面交点至基准孔孔心之间的偏差达到精度控制范围内。
4) 重复步骤1)~3)至3个偏差值同时达到精度可控范围内,此时,基准孔孔心在OF坐标系下的坐标为
(12)
式中:x′、y′由相机测量到圆孔中心在OF坐标系下的坐标由式(5)计算获得,满足
(13)
记此时所对应的机器人驱动坐标为p,末端方向的单位向量为v,则按照2.1节设定的孔心坐标系定义规则,即式(6)~式(9),可实现v向旋转矩阵的计算,记此时OP坐标系向OR坐标系变换的旋转矩阵为R′,则基准孔孔心实际位置所对应的机器人驱动坐标为
(14)
将式(11)和式(14)代入式(10)可计算得基准孔对应的机器人驱动误差。
上述方法中,根据相机和激光传感器的实时测量反馈,控制相机到达基准孔精度控制范围内的理想姿态,再确定基准孔对应的实际机器人驱动坐标,可以有效避免采用相机在机器人理论驱动坐标下(此时机器人末端姿态为图6中实际姿态)直接测量基准孔相对于刀具坐标系原点之间的偏差时,由于拍摄高度偏差及孔位局部法向误差较大引起的较大相机测量偏差,对于保证基准孔对应的机器人三维驱动偏差的测量精度十分重要。
2.3 待钻孔定位误差补偿
本节提出一种根据3个或以上基准孔的驱动坐标偏差向量,对该组基准孔邻近范围内的待钻孔进行定位误差补偿的方法。
图7所示为基于4个基准孔补偿待钻孔的示意图。下面以其中1组孔为例进行补偿说明,每组补偿方法相同。
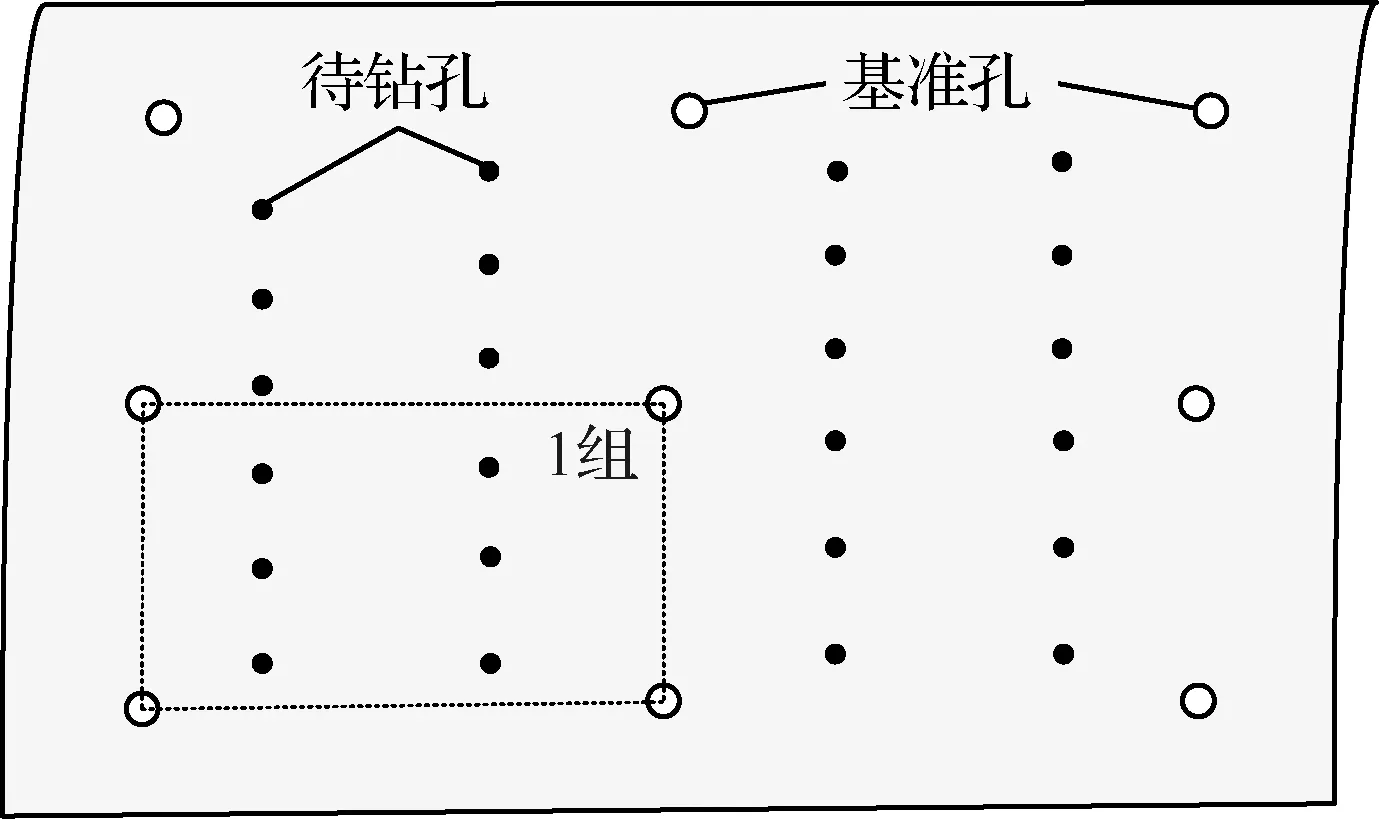
图7 基准孔与待钻孔
记4个基准孔理论驱动坐标分别为Rdt,k,k=1:4。由2.2节的方法计算得到基准孔对应的实际驱动坐标为Rdp,k,k=1:4,则可通过奇异值分解求解理论驱动坐标与实际驱动坐标之间的转换关系。具体步骤如下:
1) 求解坐标平均值
2) 构造分解矩阵A
3) 对矩阵A进行奇异值分解
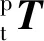
记该组中1个待钻孔的理论坐标为Rrt,本文根据基准孔理论与实际驱动坐标之间的关系对待钻孔实际驱动坐标进行重新计算,记计算后的待钻孔驱动坐标为Rra,则
驱动机器人达到补偿后的位置Rra,而不是待钻孔的理论驱动位置Rrt,从而完成对待钻孔位置误差的补偿,对于待钻孔局部的法向误差可以在刀具实际达到待钻孔表面后再次进行法向调节,以确保制孔垂直度精度。
3 实验验证
对上述视觉辅助下的机器人制孔定位误差补偿方法进行了验证实验。实验使用的是德国KUKA公司生产的KR30-3型6自由度工业机器人;相机为德国AVT公司生产的GC2450M型号相机与施耐德公司生产的KREUZNACH APO- XENOPLAN 1.4/23-0903型号镜头,图像分辨率为2 448×2 050;激光测距传感器为德国Baumer公司生产的OADM 12I6460/S35A型号传感器,测量范围为16~120 mm,线性误差为±0.015~±0.35 mm,为抑制随机误差,实验中每次法向测量均取15次测量结果的平均值;外部测量设备使用的是德国GOM公司生产的三维光学测量仪(简称ATOS);实验对象为中航工业哈尔滨飞机工业集团有限责任公司提供的飞机结构实验件;所有通信控制程序采用C++语言在Qt平台编写。图8为实验现场图。在安装相机夹具与标定板之前,已由ATOS对机器人基坐标系OR及法兰中心点等进行了测量,具体方法见文献[17]。刀轴以精加工圆杆替代,刀轴实测直径dT为4.69 mm,安装情况见图2。安装后测得刀尖部分距离OP坐标系原点77.84 mm,刀轴在OF坐标系下的方向经测量为(0.000 23,-0.001 1,1.000 0),可见通过机加工能够保证刀轴与OF坐标系z轴重合。

图8 实验现场
3.1 手-眼标定及验证
在机器人HOMO位置进行相机标定时(见图2),获得标定图像如图9所示。在该时刻由测量系统测得h的值为186.60 mm。
图9中按编号对应的9孔阵列在OF坐标系下的坐标可由第2节方法首先测量标定板定位孔,然后根据坐标系关系进行坐标转换得到,转换结果如表1所示。由表1可得9孔阵列z坐标值分布在186.50~186.73 mm,平均值(h的计算值)为186.61 mm,即标定板工作面与法兰盘平面之间的平行度偏差仅为0.11 mm,h计算值与测量值偏差为0.01 mm,符合坐标转换精度要求。本文最终设定OF坐标系原点至标定板工作面的距离h为186.61 mm。
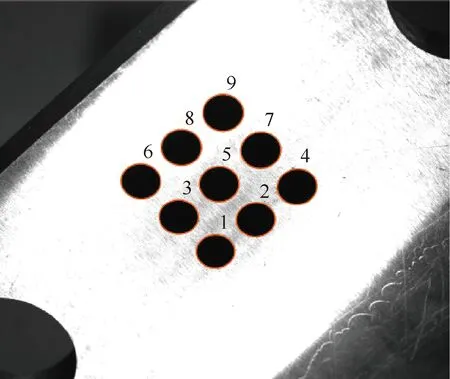
图9 相机标定图像
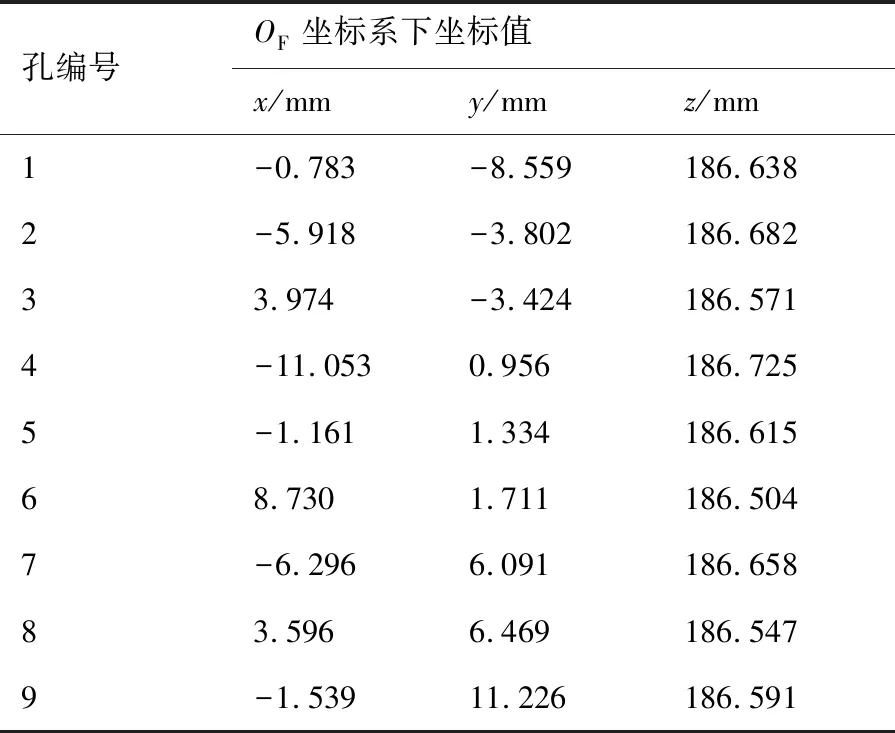
表1 9孔阵列在法兰坐标系下的坐标
按式(5)进行单应矩阵H的计算,为验证此时单应关系H的准确性,本文通过9孔阵列中任意8个孔的中心点坐标与其对应的笛卡尔坐标进行单应关系H计算,即
然后以剩余的1组圆孔中心点作为验证,通过H计算出(u9,v9)对应的笛卡尔坐标与实际笛卡尔坐标FpN,9进行比较,表2所示单应关系H的验证结果。
由表2可见,采用本文所提出的单应方法对9孔阵列区域内的圆孔中心点进行坐标测量是可行的。因此,最终以9个孔心坐标进行单应H计算,得
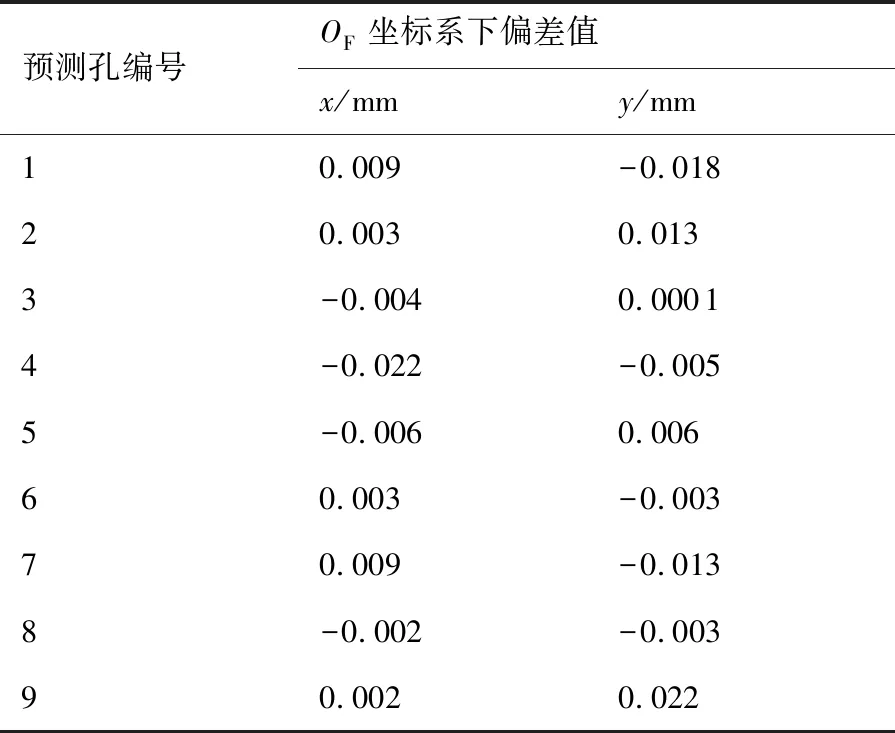
表2 单应矩阵精度验证
3.2 补偿验证
3.2.1 实验件说明
飞机结构实验件实物如图8所示。为了方便模拟制孔误差补偿效果的实验验证,实验件上所有待钻孔已经根据理论位置预先完成了加工,并在实验前采用ATOS测量系统对实物进行了测量,得到的数模如图10所示。待钻孔孔径的实际测量值如表3所示。为方便说明,对于图10中已经加工出的绿色圆孔,以下仍称为待钻孔。
选取实验件中6个基准孔和8个待钻孔进行孔位误差补偿测试,图10中红色圆孔(标号101~106)表示基准孔位置,绿色圆孔(标号1001~1008)表示待钻孔位置,根据位置关系,将补偿对象分为两组,记为组1和组2:
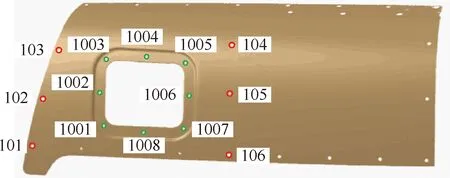
图10 实验对象数模
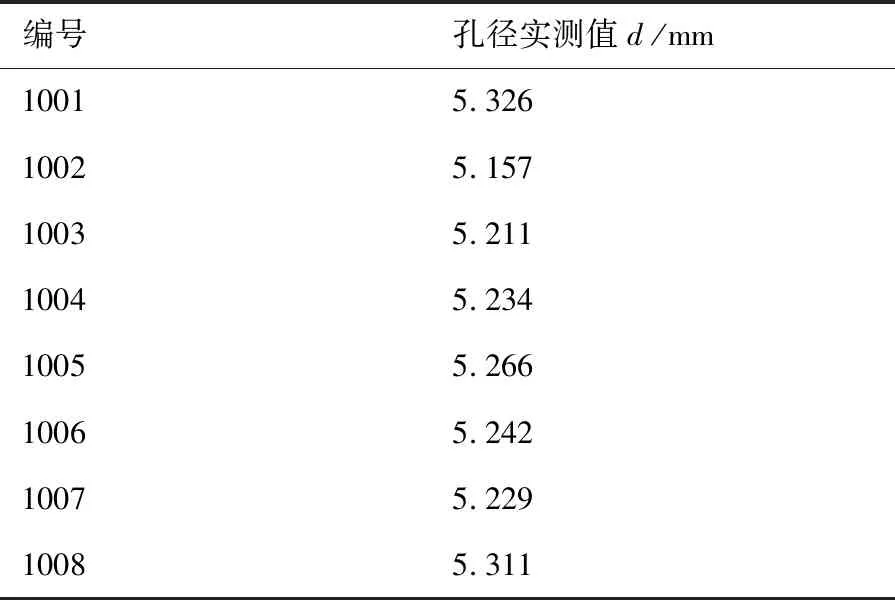
表3 待钻孔孔径
组1基准孔为101,102,105,106;待钻孔为1001,1006,1007,1008。
组2基准孔为102,103,104,105;待钻孔为1002,1003,1004,1005。
实验中以图10所示的实测数模作为实验件的理论数模,以消除待钻孔加工误差对精度评估结果的影响。该实验中制孔定位的综合误差来源主要含工件找正误差和机器人自身的运动误差。
3.2.2 补偿前待钻孔定位误差评估
首先对误差补偿前待钻孔的系统综合定位误差进行了评估。驱动机器人按待钻孔孔心在OR坐标系下的理论坐标运动至孔位上方处,进行误差测量,以待钻孔1001为例进行说明,如图11所示。
本文设计的安装结构保证了刀具轴线方向穿过激光传感器的激光点所围成的四边形的中心区域,因此在图11所示的机器人姿态下,通过激光测距传感器测量得到的4个激光点在OF坐标系下的z坐标值的平均值即可表示拍摄高度h′,定义拍摄高度方向上的偏差eh=h′-h,在图11所示姿态下,测得测量高度偏差为eh=1.73 mm,由4个激光点坐标拟合平面获得平面法向在OF坐标系下的方向,通过与刀具轴线方向,进行夹角计算可获得偏差角度θ=3.93°,通过对图11进行图像处理并由式(13)可计算的孔心的相机测量偏差为e2D=2.00 mm,则此时孔心与OP坐标系原点之间的偏差可表示为
其他待钻孔补偿前测量结果如表4所示。

图11 待钻孔1001补偿前定位误差评估
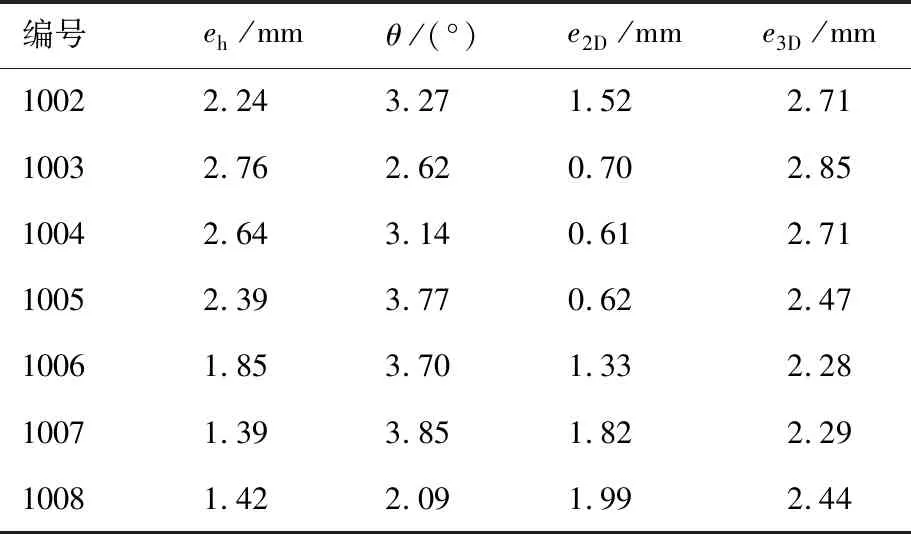
表4 待钻孔补偿前定位误差
由表4可见,补偿前待钻孔3D定位误差范围为2.28~2.85 mm,平均为2.55 mm,法向误差范围为2.09°~3.93°,平均为3.30°,2D误差范围为0.61~2.00 mm,平均为1.32 mm。
3.2.3 基准孔驱动误差测量
完成待钻孔误差检测之后,按照2.2节的方法分别驱动机器人对组1和组2的基准孔所对应的机器人三维驱动误差进行测量,以孔101为例进行说明。
图12为孔101坐标测量计算过程,机器人按理论坐标首先到达指定位置(图6中所示的机器人实际到达姿态),获得如图12(a)所示相机图像,可见激光点中心与孔心之间存在明显偏差,对圆孔中心进行提取并以计算获得的手-眼关系进行计算偏差计算,所有测量结果已显示在图12(a)中;然后根据激光测距传感器及图像反馈进行闭环伺服控制,调整机器人末端姿态直至满足要求(图6中所示的机器人理想到达姿态),测量结果如图12(c)所示,可见通过本文所提出的手眼关系可以有效地对机器人制孔位置误差进行反馈,图12(d)为最终圆孔中心提取结果,其中(u,v)表示圆孔中心的像素坐标值。基准孔误差情况如表5所示。

图12 基准孔101实际驱动坐标测量
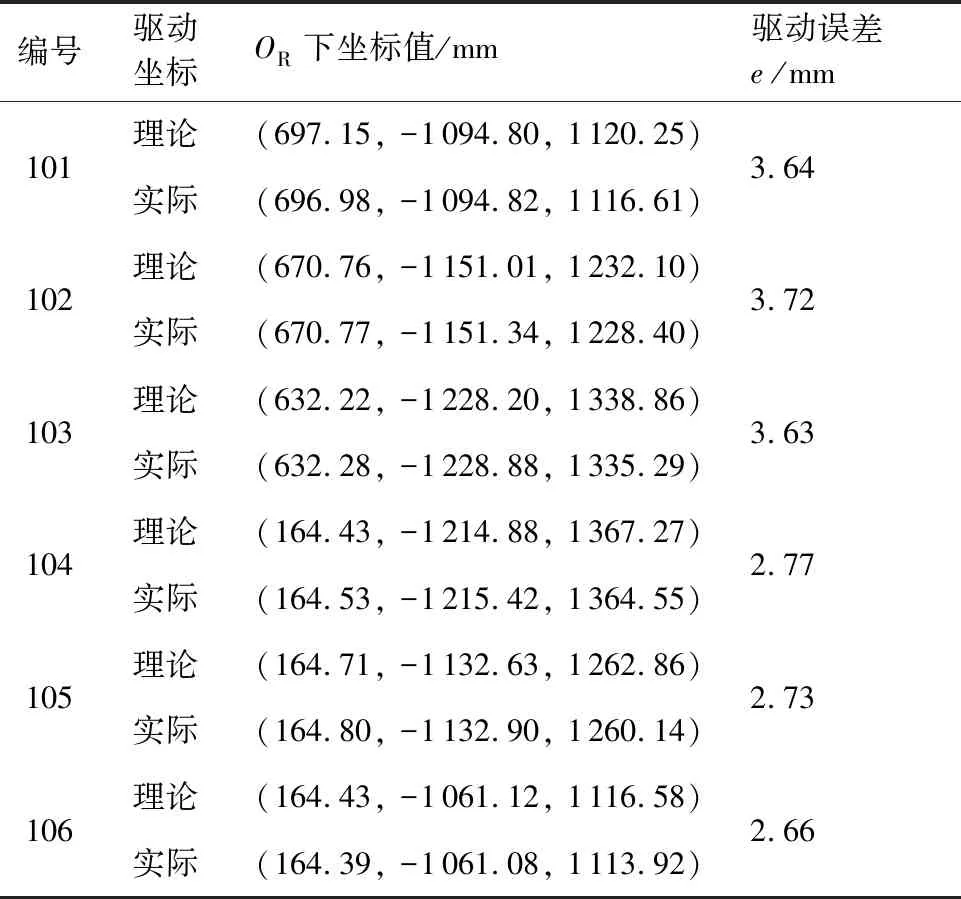
表5 基准孔对应的机器人驱动坐标情况
3.2.4 待钻孔定位误差补偿
将表5所对应的坐标数据代入2.3节进行机器人理论驱动坐标与实际驱动坐标的旋转平移变换计算,以获得的式(15)和式(16)对待钻孔1001~1008的方向和位置Rra进行计算并作为待钻孔新的方向和位置,驱动机器人按照新的位置行驶至指定位置进行测量。
图13所示为待钻孔1001补偿后测量结果,可见补偿后拍摄高度偏差eh= 0.11 mm,相机测量偏差e2D=0.09 mm;调整法向后θ=0.31°,eh=0.07 mm,e2D=0.06 mm。其他待钻孔测量结果如表6所示,表中加粗字体表示补偿后的误差情况。
可见补偿后相机测得的孔位位置误差范围为0.03~0.15 mm,平均值为0.08 mm,相比于补偿前相机测量到的2D误差范围为0.61~2.00 mm,平均为1.32 mm,补偿后的二维误差大大减小。因此,通过本文手-眼标定方法对基准孔对应机器人驱动坐标误差计算后获得的三维误差变换矩阵可高效地完成基准孔邻域范围内的待钻孔定位误差补偿。

图13 待钻孔1001补偿后定位误差
3.2.5 模拟制孔
为进一步验证补偿方法的有效性,按照机器人在待钻孔处的最终姿态,带动刀轴进行模拟制孔工作。如图14所示,为实验中模拟制孔图像。
根据刀尖点与OP坐标系原点之间的距离和本文设定的h值,实验中设定法兰盘沿孔方向的进给量为87 mm,此时刀轴进入每个待钻孔孔位的深度为87 mm-77.84 mm=9.16 mm。

图14 模拟制孔

图15 模拟制孔效果图
图15所示为刀轴进入待钻孔之后,从孔位另一侧拍摄到的效果图。由图可见,对所有待钻孔,刀轴进给87 mm均可准确进入,其中仅待钻孔1006的边缘与刀轴贴合,其余孔均与刀轴之间存有一定缝隙,说明:
1) 制孔位置误差小于各孔直径与刀轴直径下限的差值的1/2。
2) 制孔位置误差小于模拟制孔前最终姿态的法向偏差在进给87 mm后的位置偏差加上最终姿态时的位置偏差。
以待钻孔1006为例,对于上述说明1),位置误差具体计算为
对于说明2),位置误差具体计算为
因此在待钻孔1006处制孔,位置误差不超过0.21 mm。
对于制孔垂直度精度的验证,由于法兰盘沿孔方向进给87 mm仍可使刀轴被准确放入待钻孔中,因此模拟制孔的偏差角度应小于最大位置误差与轴向进给量的比值。以待钻孔1006为例,具体计算为
按上述计算方法,对所有待钻孔进行制孔后姿态误差计算,汇总结果如表7所示,表中加粗字体表示计算后的模拟制孔的姿态误差。
由表7可见,模拟制孔的制孔最大及平均位置误差分别减小至0.32 mm和0.28 mm以内,最大和平均法向误差分别减小至0.21°和0.17°以内。由于上述误差值为各孔位的最大误差估计值,且由图15可见,本文模拟制孔后除孔1006外,其余各孔均与刀轴之间存有一定缝隙,因此本文模拟制孔的误差可确定为0.30 mm、0.21°以内,能够满足航空制孔的制孔精度要求。
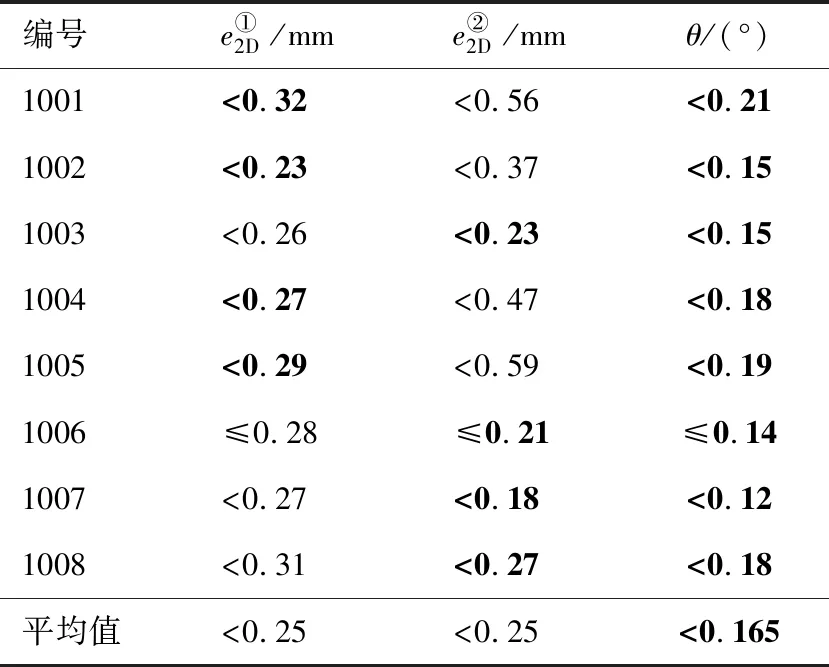
表7 模拟制孔姿态误差
4 结 论
1) 提出了一种机器人制孔孔位误差在线视觉补偿方法,利用相机图像平面与制孔工作平面之间的单应矩阵表征手-眼关系,并提出了简便易行的手-眼标定方法。
2) 利用相机以一定倾斜角度安装,可实现机器人直接带动刀轴到达指定基准孔位置状态下进行误差快速实时测量,自动化和集成化程度更高。
3) 由于误差的测量和变换均建立在三维空间,因此该方法适用于对曲面结构上的制孔定位。
4) 在对飞机结构实验件的8个待钻孔的模拟钻孔实验中,位置和法向误差范围补偿前为2.28~2.85 mm和2.09°~3.93°,平均为2.55 mm和3.30°,补偿后减小到最大误差分别不超过0.30 mm 和0.21°,验证了采用本文方法提高机器人制孔定位精度的有效性。
