超高速干气密封扰流效应及抑扰机制
2019-10-31王衍胡琼肖业祥黄国庆朱妍慧葛云路
王衍,胡琼,肖业祥,黄国庆,朱妍慧,葛云路
1. 江苏海洋大学 机械与海洋工程学院,连云港 222005
2. 清华大学 水沙科学与水利水电工程国家重点实验室,北京 100084
3. 清华大学 能源与动力工程系,北京 100084
干气密封(Dry Gas Seal, DGS)的工作机理和特点决定了此类密封更适宜在高速工况下使用,高转速使其具有更加优良和稳定的动压性能[1-3]。2012年,干气密封技术在美国能源部《2012年小型企业新技术开发与技术转移指导书》中被列为美国“先进燃气轮机封严与密封控制的战略方案(Advanced Gas Turbine Sealing and Leakage Control Strategies)”,干气密封产品在被用来替代PW2000型发动机原有的接触式机械密封件后,在美国联合航空公司试飞数千小时完美无损,远胜原件。目前,干气密封技术作为先进密封技术之一也被列举在中国高新技术条目中。
干气密封技术源于气浮轴承的非接触承载机理[4],其实际应用工况远没有气浮类轴承严苛,许多高工况时气浮轴承面临的微振动、扰流等情况在干气密封中尚未被完全发现或考虑[5-6]。近年来,干气密封技术伴随超高速气浮轴承逐渐尝试应用于(微型)燃气轮机、高速陀螺仪及航空发动机等超高速设备中,超高速、微尺度工况下内部气体复杂流动引起的压力扰动已成为束缚气体润滑性能提升的关键。针对这一现象,国外学者Aoyamae等[7]认为是由于润滑气体的流动形态改变而导致的,Yoshimura等[8]的试验和仿真结果进一步表明,雷诺数增大时,润滑流体压力波动增大,扰动现象越显著;国内学者张鸣等[9]在研究进一步提升精密气浮平台精度的过程中将扰流振动原因归为湍流因素导致的气体压力波动,并指出改善流道设计参数可有效抑制非稳定流动;相关最新研究[10-12]也表明,表面粗糙度和形貌的合理设计、重构对改善表面性能至关重要,有助于进一步提高密封的稳定性。
基于此,本课题组通过深入开展重构干气密封槽底织构造型以改善流体流动、降低扰流效应的相关研究[13-14],初步证实了有序织构造型设计具有提升密封性能、稳定流动的有益效果。本文结合近期的研究思路和基础积累,在研究超高速干气密封微尺度流场特性规律的基础上,充分探讨了导流织构对超高速工况下密封性能的影响机制和规律。以期为有效提升超高速工况下干气密封的运行稳定性提供理论依据和参考。
1 理论模型
1.1 模型假设
本研究模型做如下假设:
1) 密封介质在界面无相对滑动。
2) 不考虑惯性力与离心力的作用效果。
3) 间隙气膜为连续流体,为完整的流体膜润滑。
4) 气膜热状态等温,忽略温度和压力等对黏度的影响。
5) 密封副在运行过程中始终保持平行,除槽底面之外的其余表面理论光滑。
对于超高速工况,需要对假设2进行评估,依据经典文献[15],是否考虑惯性力和离心力影响的判断公式为
(1)
式中:Re为雷诺数;ρ、U、μ分别为流体的密度、流速与黏性系数;l为特征长度;h为密封副间膜厚。当Re与l/h可比拟或处于同一数量级时,必须考虑惯性力和离心力的影响,如果差距较大,即可忽略惯性力的影响。
对于干气密封:将U类比为平均旋转线速度v(计算方法见1.2节),其他参数选择文献[16-17]中经典螺旋槽的几何参数,如表1所示。操作参数值取表1中研究工况的上限值:密度ρ=1.29 kg/m3,黏度μ=1.86×10-5Pa·s,膜厚h=2 μm,转速N=12×104r/min,l=ro=77.78 mm。代入式(1)求解得Re=118.64≪l/h=38 890,两者相差2个数量级,所以本文工况参数下的惯性力和离心力可以不考虑。
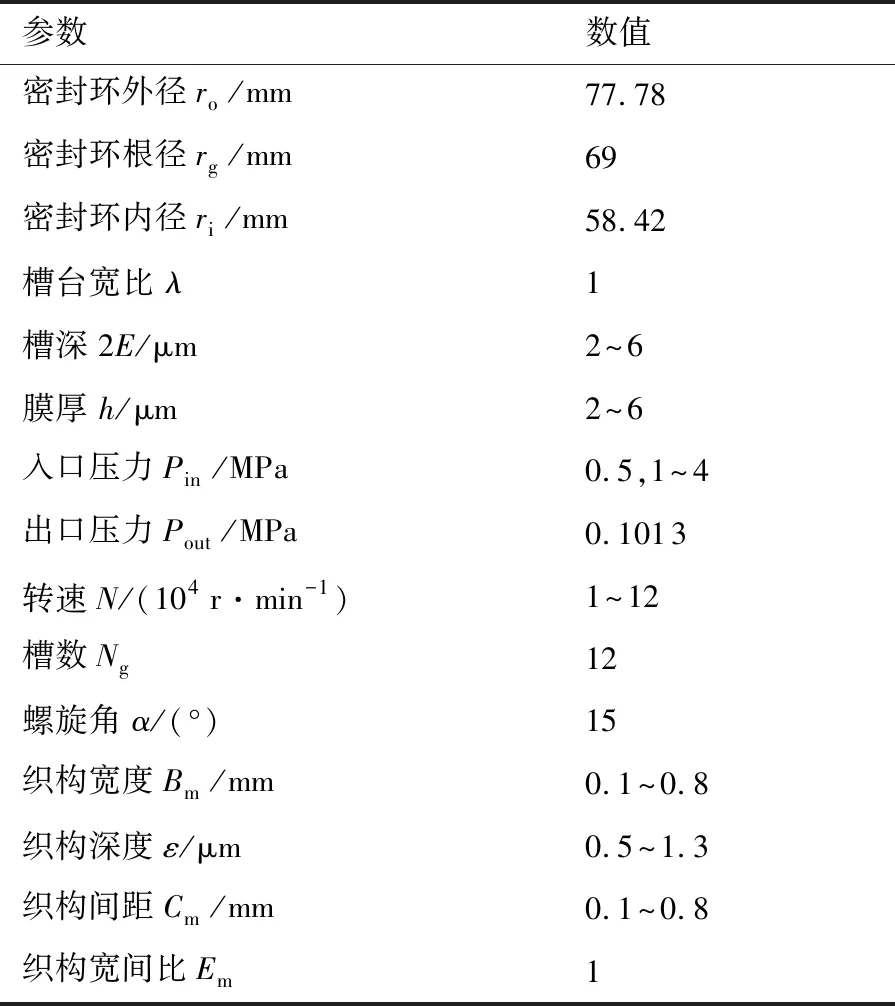
表1 数值仿真参数
1.2 超高速的定义
根据机械密封使用工况及参数分类标准[18]:当密封端面线速度v<25 m/s时为一般速度工况,25 m/s≤v≤100 m/s时为高速工况,v>100 m/s时为超高速工况。根据本文定义的密封几何参数(见表1),端面线速度与转速的关系为
(2)
求解后可得到与v=100 m/s对应的转速N=14 030 r/min,即可认定在本文几何参数下,N>14 030 r/min时即为超高速工况。
1.3 数值计算方法
采用商用CFD软件Fluent进行密封性能分析。目前,关于干气密封微尺度流场流态的确定,部分学者得出[19-20],当入口压力Pin=0.4~0.5 MPa、转速N=10 000 r/min左右时,实际流态选择为层流与实际更为符合;部分学者[21-22]在压力较高(Pin=4.585 2 MPa)、转速N=10 000 r/min左右时,则选用湍流形式进行求解计算。本课题组通过计算研究发现,从整体而言,不同的流态虽然对计算结果具体数值影响较大,但不会改变相关参数的影响规律。
鉴于文中压力和速度取值较大,本文对干气密封微尺度下的流态假设为湍流形式。依据干气密封运行工况及条件,选用RNG(Re-Normalization Group)k-ε湍流模型。气膜流动控制方程通用形式为[23-24]
(3)
式中:u为速度矢量;φ为任意变量的标量值;Γ为扩散系数;S为源项。
1.4 物理模型
选择广泛应用的螺旋槽型干气密封[25-26](Spiral-Dry Gas Seal, S-DGS)为研究对象,同时参考课题组目前研究的导流织构设计方法[13]。流槽周向均匀分布于整个密封端面,导流织构沿螺旋槽形状均匀分布于螺旋槽底部,旋转角速度ω方向为逆时针(如图1(a)所示)。织构参数定义如图1(b)所示。因密封端面流槽成周期性分布,为提高计算效率,可选择一个周期内的具有织构造型的螺旋槽(Texture Spiral-Dry Gas Seal, TS-DGS)区域为建模和计算区域。采用面体网格逐次拉伸的方法生成网格模型[27],如图2(a)所示。边界条件如图2(b)所示,其中AB为内径侧大气压出口边界,CD为外径侧介质压力入口边界,Γ1和Γ2为周期边界,与静环贴合的面为静止壁面,与动环贴合的所有面(含槽区)为旋转壁面。
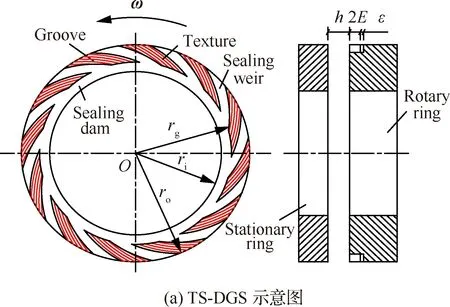
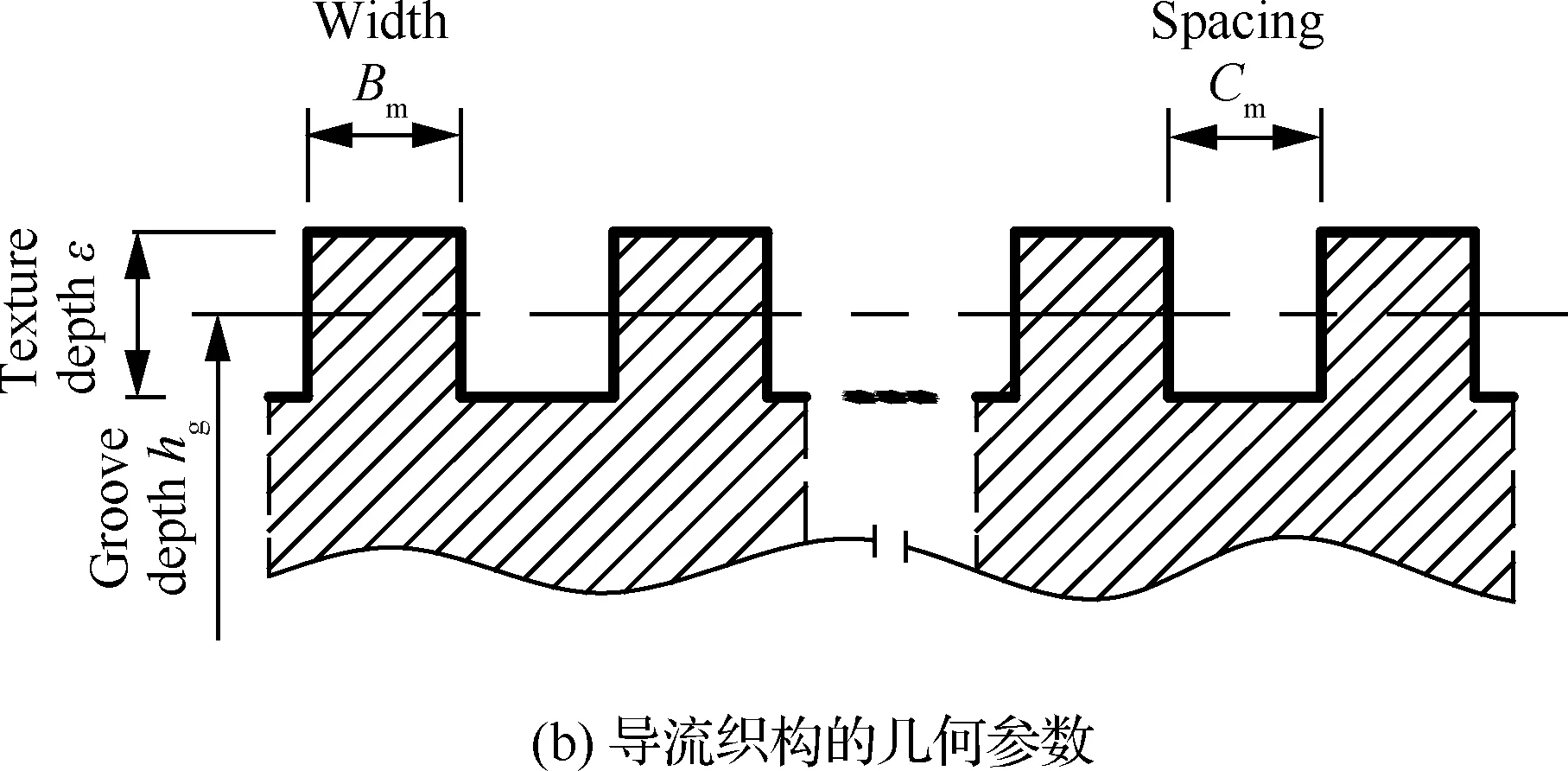
图1 TS-DGS物理模型
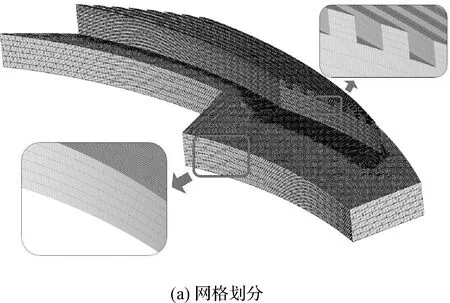
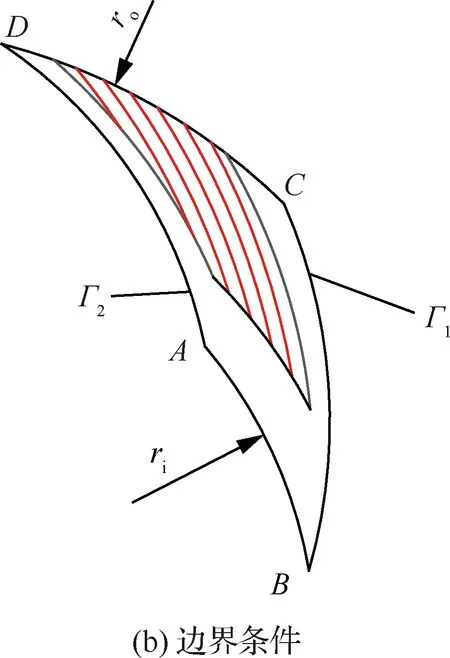
图2 计算模型网格划分及边界条件
2 超高速下密封性能分析
2.1 计算方法验证
为了验证计算方法的正确性,选择文献[16-17]中经典螺旋槽的几何参数为模型建立依据,密封介质选择理想气体。分别进行网格无关性分析及性能参数验证性试验,验证了本文方法及参数设置的正确性,具体见文献[27]。
本文研究工况参数区间除了完全涵盖文献[16-17]中对应区间以外,在压力和转速方面都有更大范围的扩展,根据文中的转速取值,定义相邻转速间对应开启力的变化百分比η为
(4)
图3所示为转速范围为10 000~100 000 r/min时3种膜厚的η值随转速增大的变化规律。从图中可以看出,随着转速增大,η始终为正值,但数值逐渐减小;当膜厚h=5.08 μm,N≥70 000 r/min时,η≈0。这一现象说明,开启力的大小随转速的升高持续增大,但增幅随转速升高呈逐渐降低的趋势,换言之,一定工况下,开启力随转速的升高将不再持续增大。由不同膜厚下的η值变化还可以看出,膜厚越小,η值波动越大,说明气膜微尺度时的流动愈加复杂。
图4和图5为在相同工况和几何参数下,有/无导流织构的槽底压力分布及槽底速度流场分布。图4中,在Pin=3 MPa、h=4 μm、2E=2 μm、N=40 000 r/min时,无导流织构的压力云图峰值小于有织构造型的(3.066 MPa<3.112 MPa),二者高压区均分布在槽区,对于提高密封性能和运行稳定性有积极意义。
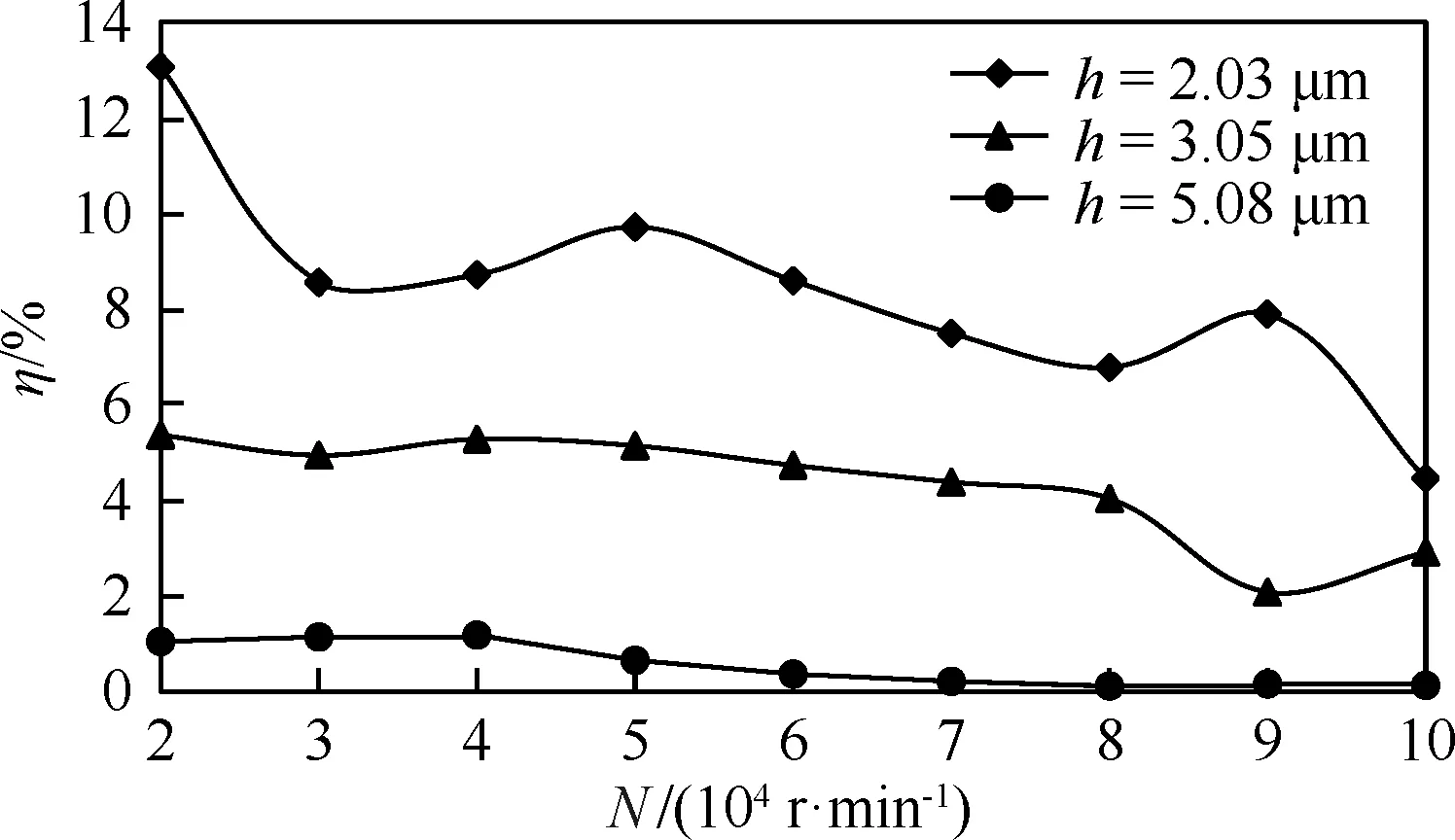
图3 S-DGS微尺度扰流验证分析(Pin=4.585 2 MPa)
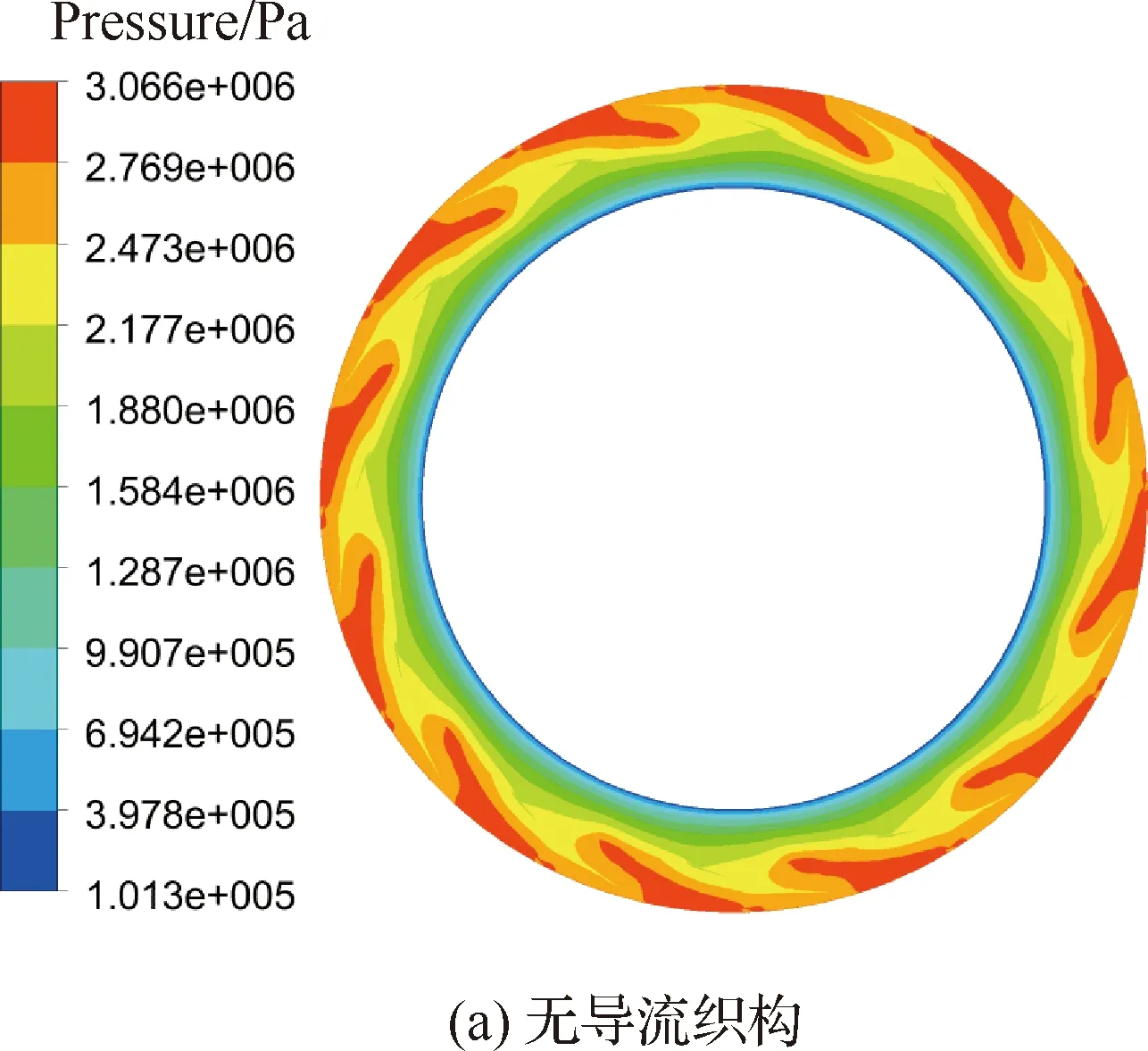
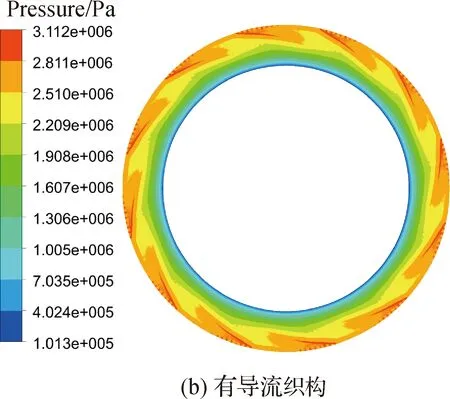
图4 有/无导流织构槽底压力分布
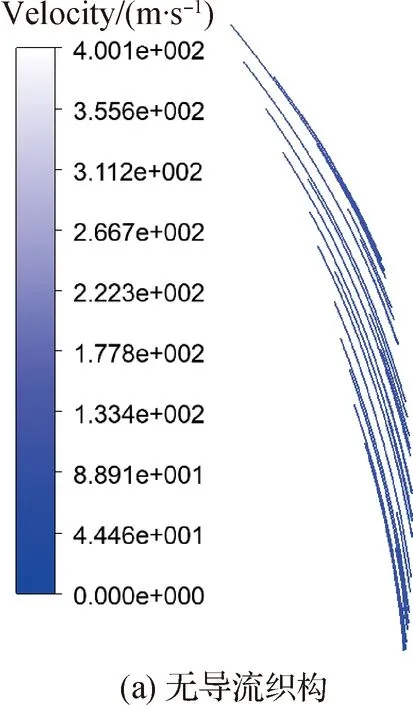
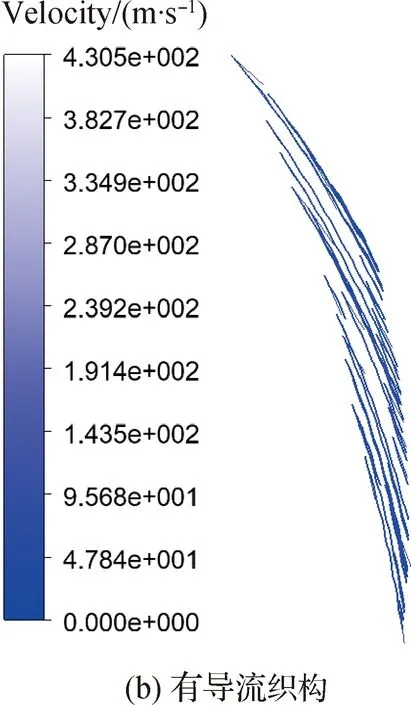
图5 有/无导流织构槽底速度分布
由图5可以看出,同一截面下的S-DGS和TS-DGS槽底流场流线方向均从外径入口指向槽底根部,但后者的最高速度更高(由图可以看出速度对比为430.5 m/s>400.1 m/s)。可见,导流织构对流体流动具有较好的驱动、导流效果,在流体流动出现波动时较强的驱动效果可以在一定程度上抵消或削减波动的影响,进而起到稳定流体流动的作用,具体见下文计算结果。
2.2 超高速下扰流特性分析
为了全面获得微尺度、高参数下的干气密封扰流特性,分别从变压力(Pin=0.5~4 MPa)、变膜厚(h=3~6 μm)、变槽深(2E=2~6 μm)及变转速(N=10 000~120 000 r/min)4个方面进行系统分析。
图6所示分别为变压力、变转速下S-DGS开启力(Fo)和泄漏量(Q)的变化规律。图中显示,N≤45 000 r/min时,开启力随转速持续增大,当超过该值时,开启力开始随转速缓慢下降(负相关);当转速达到90 000 r/min左右,开启力又与转速呈正相关关系,且这样的变化趋势随压力增大越发明显。这与目前普遍存在[28-29]的中低速下开启力、泄漏量随转速升高而增大的结论有所不同,造成这一变化的原因可能是随着各参数的变化,微尺度下的流体流动出现了波动现象。具体分析如下:一定范围(N≤45 000 r/min)内的流体流动主要为稳态,存在少量、微弱的扰流因子,此时转速的增大对流体流动的驱动导流效果大于扰流效果,整体对开启力起促进作用;当转速进一步增大后,流动波动性增强,扰流效应开始大于转速对流体的驱动导流效应,进而使此时的开启力变化与转速的增大不再呈正相关关系;当转速继续上升到某一值(N=90 000 r/min左右)时,开启力、泄漏量与转速又恢复为正相关关系,本文暂定义为二次拐点现象,说明此时的导流效应增强,即超高转速对流体的驱动导流效应又超过了此时的扰流效果。
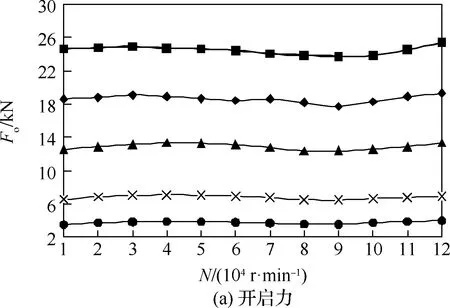
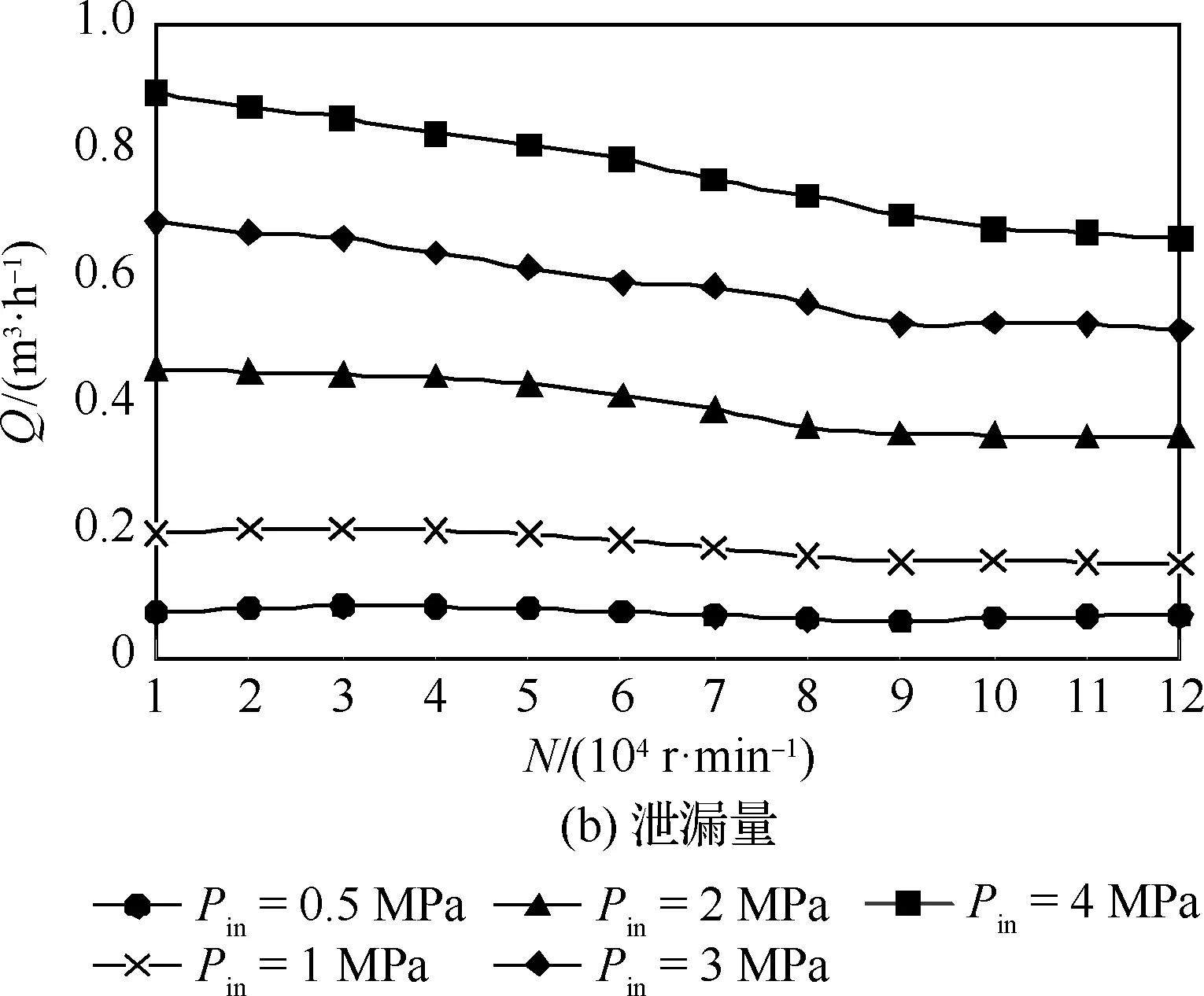
图6 不同压力下的扰流效应(h=5 μm, 2E=4 μm)
由以上分析可以得出:
1) 微尺度流场在超高速工况的流动复杂性很高。
2) 超高速工况下,至少存在两次以上拐点现象。
从图6(b)可以看出,泄漏量随转速的变化规律也较复杂,在压力较低(Pin≤1 MPa左右)时,随转速增大先是缓慢增大然后缓慢下降直至基本稳定;当压力较高(Pin≥2 MPa左右)时,泄漏量直接随转速增大而降低,只是在转速N=90 000 r/min后趋于稳定。同上述分析类似,整个变化过程的复杂性依旧源于拐点时的微尺度扰流、驱动导流效应的博弈结果。这是造成超高速时开启力和泄漏量变化规律不同于一般工况的主要原因。
同理,图7、图8分别为变膜厚、变转速和变槽深、变转速下S-DGS开启力和泄漏量变化规律。由图可以看出:与变压力、变转速工况趋势类似,在变膜厚、变转速工况时,膜厚越大,开启力与转速的负相关关系越明显,即扰流效果越显著,N=90 000 r/min左右为正负相关性转换的拐点,小于或大于这一值时,转速与开启力和泄漏量的作用关系均会出现突变;在变槽深、变转速工况时,槽深越小,扰流效果越明显,当槽深2E≤4 μm时,拐点转速提前到80 000 r/min,且拐点次数随槽深减小而减少。
综上可知,干气密封微尺度时的流体流动情况复杂,当转速达到某一值后,开启力和泄漏量不再与转速正相关,期间的扰流作用效果不可忽视;在超高速工况下,高压、大膜厚、小槽深时的扰流效果越明显,且发生第1次拐点时的转速较小,但具体数值不定;随着转速的持续增大,即使压力、膜厚、槽深等参数的不同,第2次拐点对应的转速基本在90 000 r/min附近。
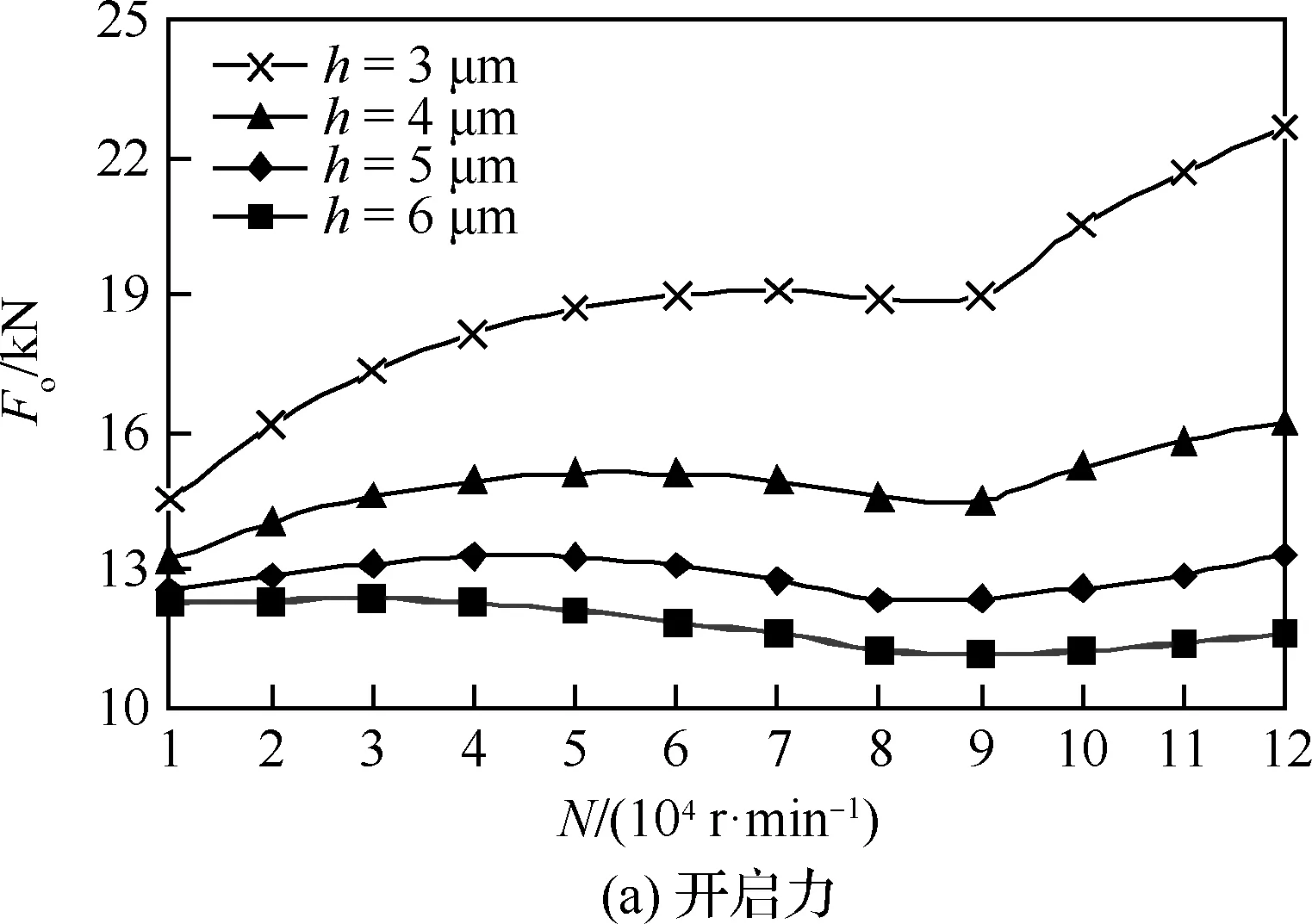
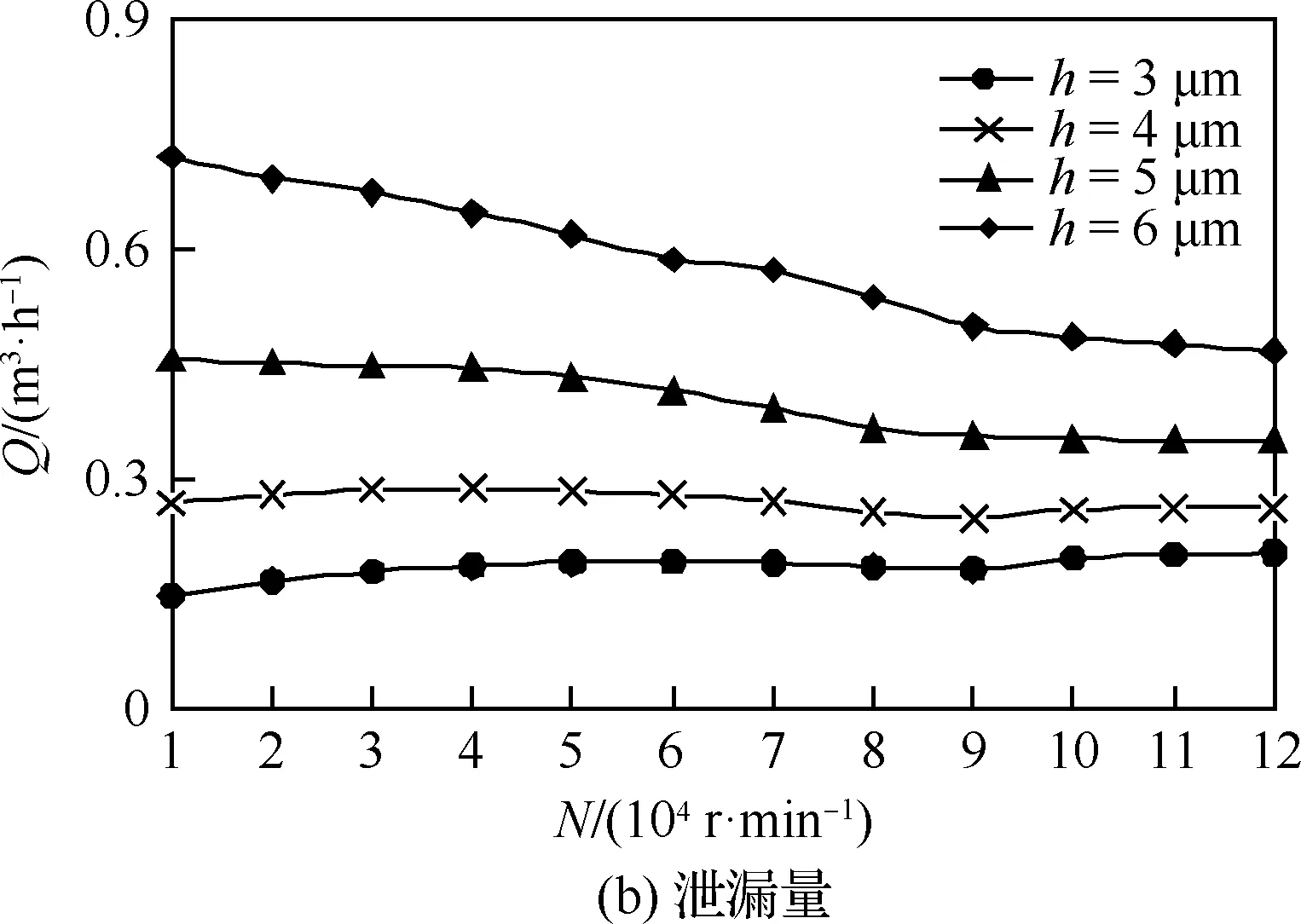
图7 不同膜厚下的扰流效应(Pin=2 MPa, 2E=4 μm)
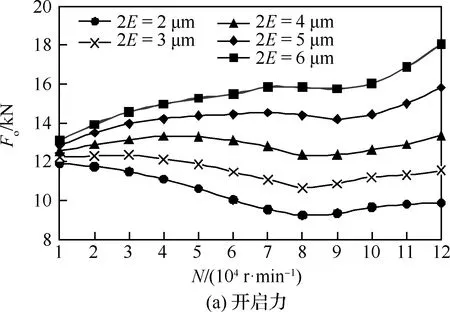
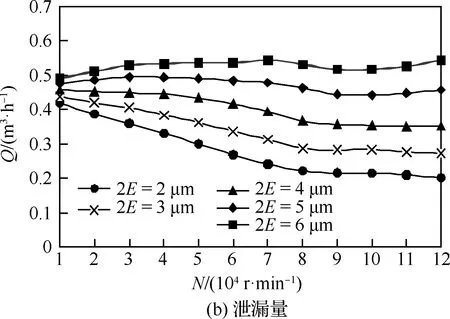
图8 不同槽深下的扰流效应(Pin=2 MPa, h=5 μm)
3 超高速下导流织构的抑扰特性
超高速下扰流特性的研究结果表明,高转速、大膜厚、小槽深及高压力时的扰流现象越明显;课题组近期研究还发现,在干气密封微尺度流动时,槽底合理的导流织构形式可有效促进流体的有序流动、提高开启性能。鉴于此,选择扰动现象较明显时的参数区间,研究此时导流织构对扰流现象的影响规律。
图9所示为槽深2E=1,2 μm,膜厚h=3,4 μm,压力Pin=3 MPa时传统螺旋槽干气密封(S-DGS)与具有织构造型的螺旋槽干气密封(TS-DGS)的开启力、泄漏量随转速的变化规律。由图可知:S-DGS与TS-DGS在超高速工况时都会出现扰流现象,开启力、泄漏量与转速为负相关关系,扰流效应强度较大;与S-DGS相比,TS-DGS具有较好的抑扰能力,其开启力和泄漏量随转速升高下降趋势不明显,具有良好的开启性能;当转速到二次拐点后,TS-DGS的流态恢复响应速度更快、开启力恢复正相关的能力(维持稳定区域的作用)更强。以上结果说明,导流织构的存在具有良好的导流效果,在扰流出现时可以进一步提升流体的规律性流动特性,不仅一定程度上降低了流体波动强度,也更容易促成二次拐点的实现,这对持续维持干气密封的稳定运行至关重要。
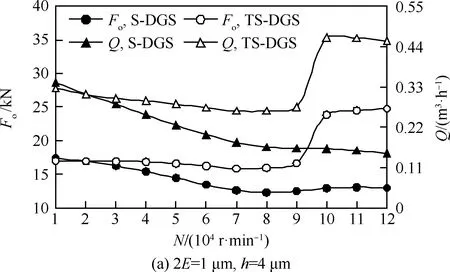
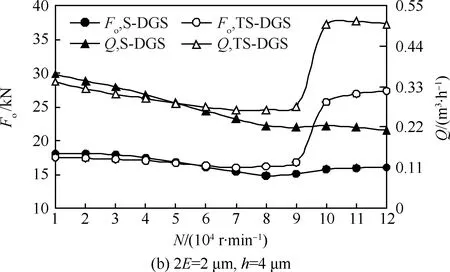

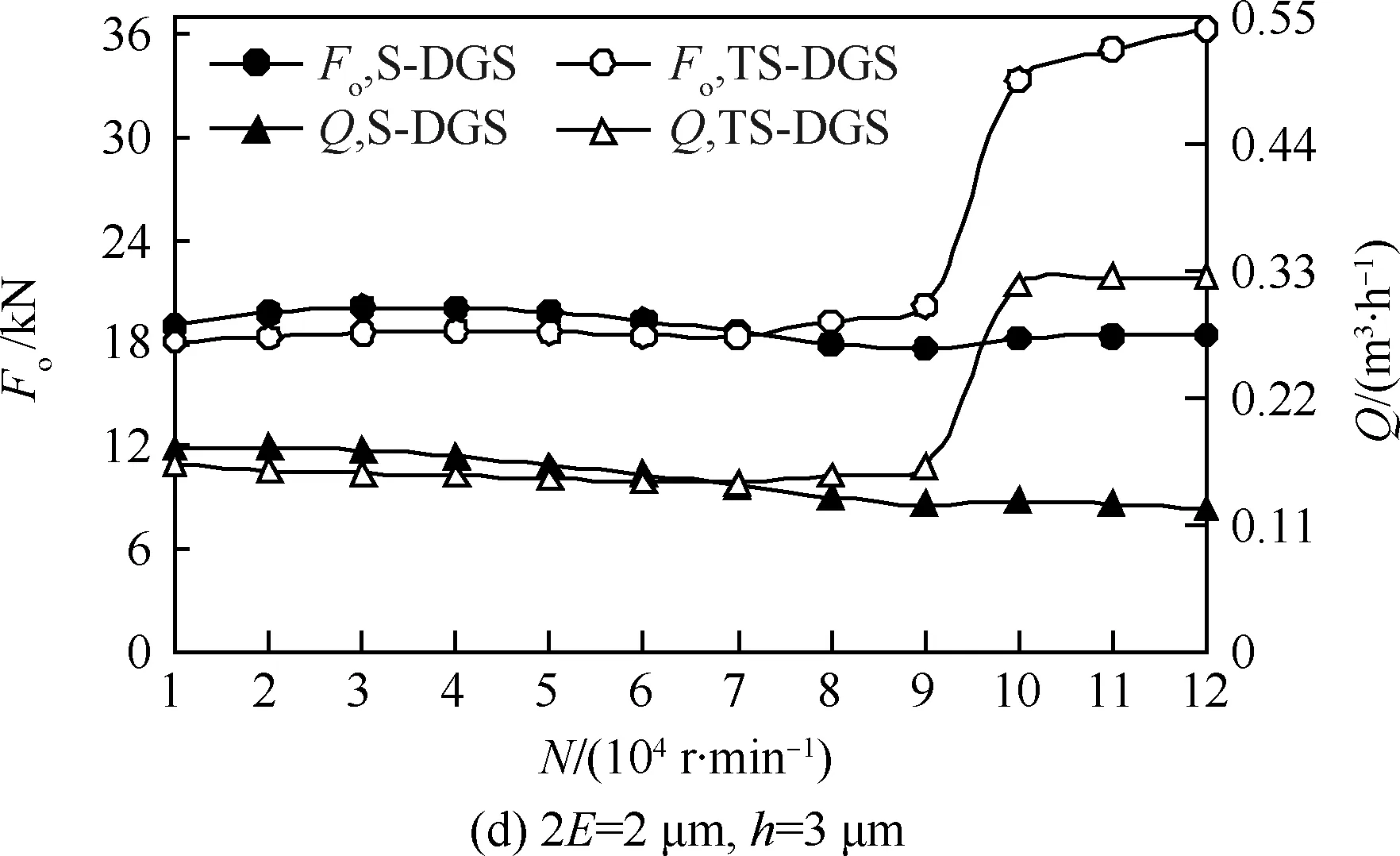
图9 扰流效应区间的导流织构抑扰特性
4 导流织构的几何参数影响规律
为进一步研究导流织构对扰流工况的影响规律和特点,选择织构深度和宽间比两个织构几何参数进行分析计算,初步探索导流织构对扰流效果的抑制机制。
4.1 织构深度
图10给出了Pin=2 MPa、h=5 μm、2E=2 μm、Bm=0.3 mm、Cm=0.3 mm条件下织构深度对开启力的影响。可以明显看出二次拐点确实发生在转速N=90 000 r/min附近。N<90 000 r/min时,开启力随织构深度的增加呈先增大后减小的趋势,在ε=0.1~0.5 μm时比较显著,并且不同转速下受扰流的影响程度不同,而ε=0.3 μm时不同转速下的开启力差值相对其他织构深度时较小,说明此时受转速扰动的程度较小。可见,ε=0.3 μm时,织构对扰流的抑制能力最好。
需要指出的是,鉴于织构深度太小会造成模型建立和网格划分的困难增大,文中对比选用的织构深度间隔为0.2 μm,对具体数值会有一定影响,但不影响整体的对比规律。
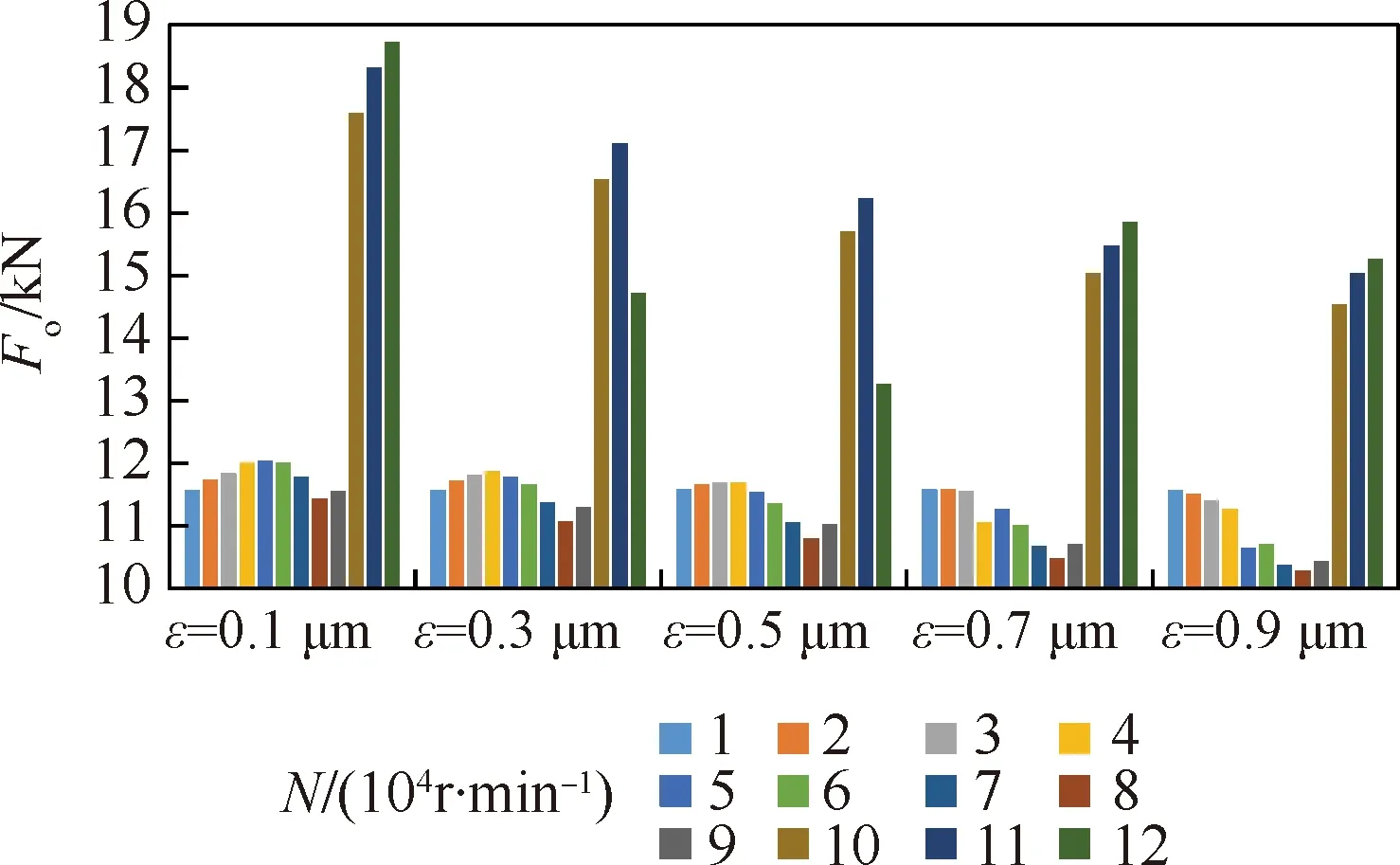
图10 织构深度对开启力的影响
4.2 织构宽间比
图11给出了Pin=2 MPa、h=5 μm、2E=2 μm、ε=1 μm条件下织构宽间比对开启力的影响。随织构宽间比Em=Bm/Cm增大,开启力增大,但当Em≥1时,开启力随此参数变化相对稳定,且扰流抑制效果在Em=1时最好。Em影响开启力的主要原因是Em的变化近似于槽深的变化,Em→∞表示槽深近似1.5 μm的光滑槽底,Em→0表示槽深近似2 μm的光滑槽底。Em影响转速扰流效应的原因则是织构具有导流作用,使扰动效应减弱。综述之,Em=1为最优宽间比。
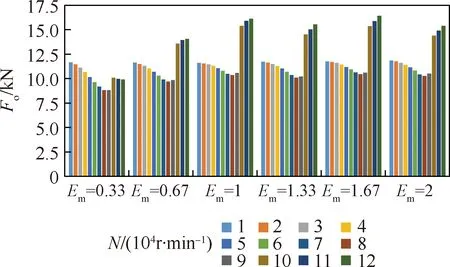
图11 织构宽间比对开启力的影响
5 结 论
1) 类似于气浮轴承的微幅自激振动现象,超高速工况时干气密封会出现开启力、泄漏量与转速的非正相关变化的扰流失稳现象。
2) 干气密封的扰流效应在高速、高压、大膜厚、小槽深时更加显著。
3) 在转速持续增大过程中,干气密封微尺度流场会出现二次拐点现象,第1次拐点随着具体工况的不同而存在一定变化,而第2次拐点基本稳定在90 000 r/min附近。
4) 导流织构在超高速下的驱动导流效应显著,具有良好的抑制扰流、维持稳定区域的作用。
