6-UCU船舶运动模拟平台的奇异位形研究与检测

高国章， 高 凯， 高 岚

(武汉理工大学 能源与动力工程学院， 武汉 430063)

船舶运动模拟平台可模拟船舶在海浪中的六自由度摇晃运动，主要用于船员培训和船舶设备测试，其结构主要是一个Stewart平台。并联机构[1]与串联机构相比有动态响应快、刚度高、精度高及承载能力强等优点，然而,随着并联机构运用到各个领域，人们发现并联机构存在一个很大的缺点,即在运行空间中存在着奇异。[2-3]当机构运行到某一空间中，其动态特性相对于全局性能发生的变化被称为奇异。[4]当并联机构处于奇异位形时，机构的自由度将会增加或减少:自由度增加会使机构变得不可控，容易对机构造成损坏；自由度减少会使机构无法达到所要的运行状态，导致不能连续运作。为设计出在可达工作空间内或工作路径中没有奇异的船舶运动模拟平台，应在设计过程中分析和检测机构的奇异性。[5]

在对Stewart平台进行奇异位形分析时，很多学者只考虑主动移动副对机构的影响，根据“输入、输出速度之间关系建立的雅克矩阵的行列式是否为0”来判断机构是否存在奇异位形，但是只根据这一条件来研究机构的奇异位形并不充分，必须把被动副考虑进来。由于螺旋理论能很好地反映机构的运动特性和约束特性，因此被广泛运用于并联机构奇异位形的分析。[5]在1991年HUNT首先提出将螺旋理论运用到机构的奇异位形研究中。赵瑞杰等[6]将反螺旋系和矩阵知识结合在一起，得到并联机构产生奇异的条件和奇异的类型。程锐[7]用螺旋理论得到并联机构产生奇异的类型，并提出利用改变驱动位置的方法来消除奇异。蔡昀宁[8]运用螺旋理论找到并联机构产生奇异的原因，并提出利用逆螺旋矩阵代替传统雅克比矩阵来寻找机构的奇异的方法。ZHAO等[9]运用逆螺旋理论提出分析并联机构奇异位形的方法，但没有考虑主动移动副对机构的奇异产生的影响。ZHAO等[9]将螺旋理论和空间静平衡理论结合在一起，提出一种末端约束对机构的奇异产生的影响，也同样没有考虑主动移动副对机构的奇异产生的影响。为正确地对机构的奇异性进行分析，本文把主动移动副和被动副虎克铰都考虑进来，以螺旋理论为基础，分析并联机构产生奇异位形的条件。

事实上，能够快速检测并联机构在可达工作空间运行时是否存在奇异位形是至关重要的。很多学者在对并联机构进行奇异位形检测时，经常采用的方法是对传统的运动学雅克比矩阵进行分析，即只考虑主动移动副产生的奇异，并没有把被动副铰考虑进来。对于双端虎克铰六自由度船舶模拟平台而言，为能更加全面地检测到平台的奇异位形，需要把被动虎克铰考虑进来。本文将提出一种有效的奇异性检测算法，最后通过相关实例分析验证所提出的遗传奇异检测算法的有效性。

1 模拟平台的奇异性分析

1.1 结构模型和坐标系的建立

双端虎克铰六自由度船舶运动模拟平台简称6-UCU(U为虎克铰，C为圆柱副)船舶运动模拟平台，由上下平台和6个连杆组成,见图1。每个连杆都通过圆柱副用上虎克铰(第i个上虎克铰铰点的中心,i=1,…,6)和下虎克铰(第i个下虎克铰铰点的中心)分别与上下平台连接。初始位置时上下平台互相平行。在上下平台的中心P和B两点分别建立局部坐标系Pxyz和静坐标系Bxyz，设P和B两点坐标为(x,y,z)T和(0,0,0)T。Px和Bx轴的正方向分别取U1U2和D1D2的中垂线方向且指向平台外部，Pz和Bz的正方向分别取垂直于上下平台的方向且方向朝上，Py和By的方向根据右手规则确定。设上平台位姿为(x,y,z,α,β,γ)T。

1.2 支路坐标系建立

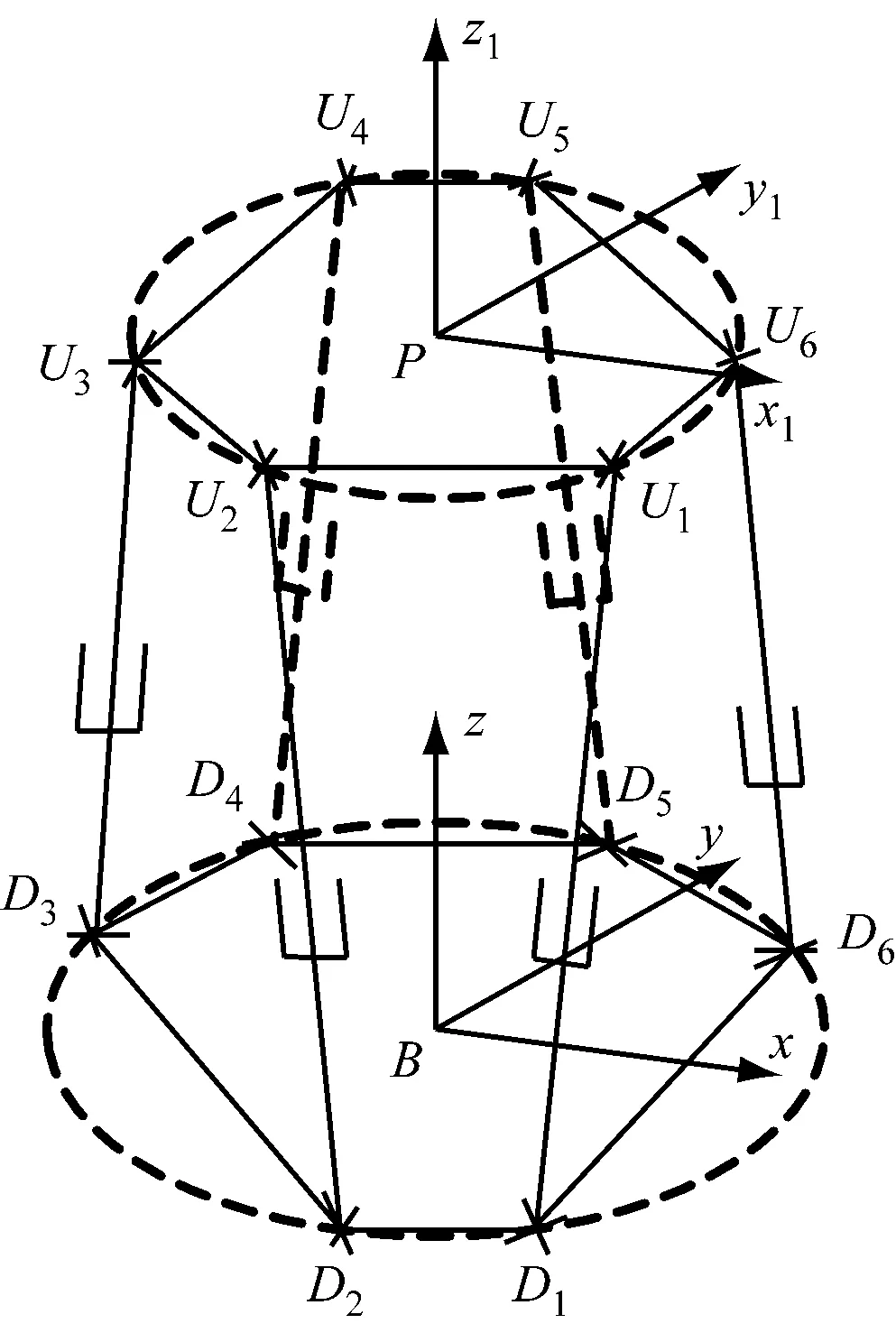
图1 机构空间结构

两个螺旋的相逆只与两个螺旋的参数有关，与原点的位置无关，即与坐标系的选择无关。因此,为方便分析机构的奇异性，建立任一支路的局部坐标系见图2，选择以与下虎克铰相连的连杆为z轴，与连杆相连的虎克铰的轴线为x轴，y轴通过右手定则得到。局部坐标系可看作是由固定坐标系Bxyz通过两次转动变换得来的，固定坐标系先绕z轴转动θ得到新坐标系Ux′y′z′，然后再绕x轴旋转δ得到局部坐标系Ux″y″z″。支路的旋转变换矩阵Rzx为

(1)

即沿连杆方向单位矢量为

(2)

式(1)和式(2)中:

zni=cosδi，

(3)

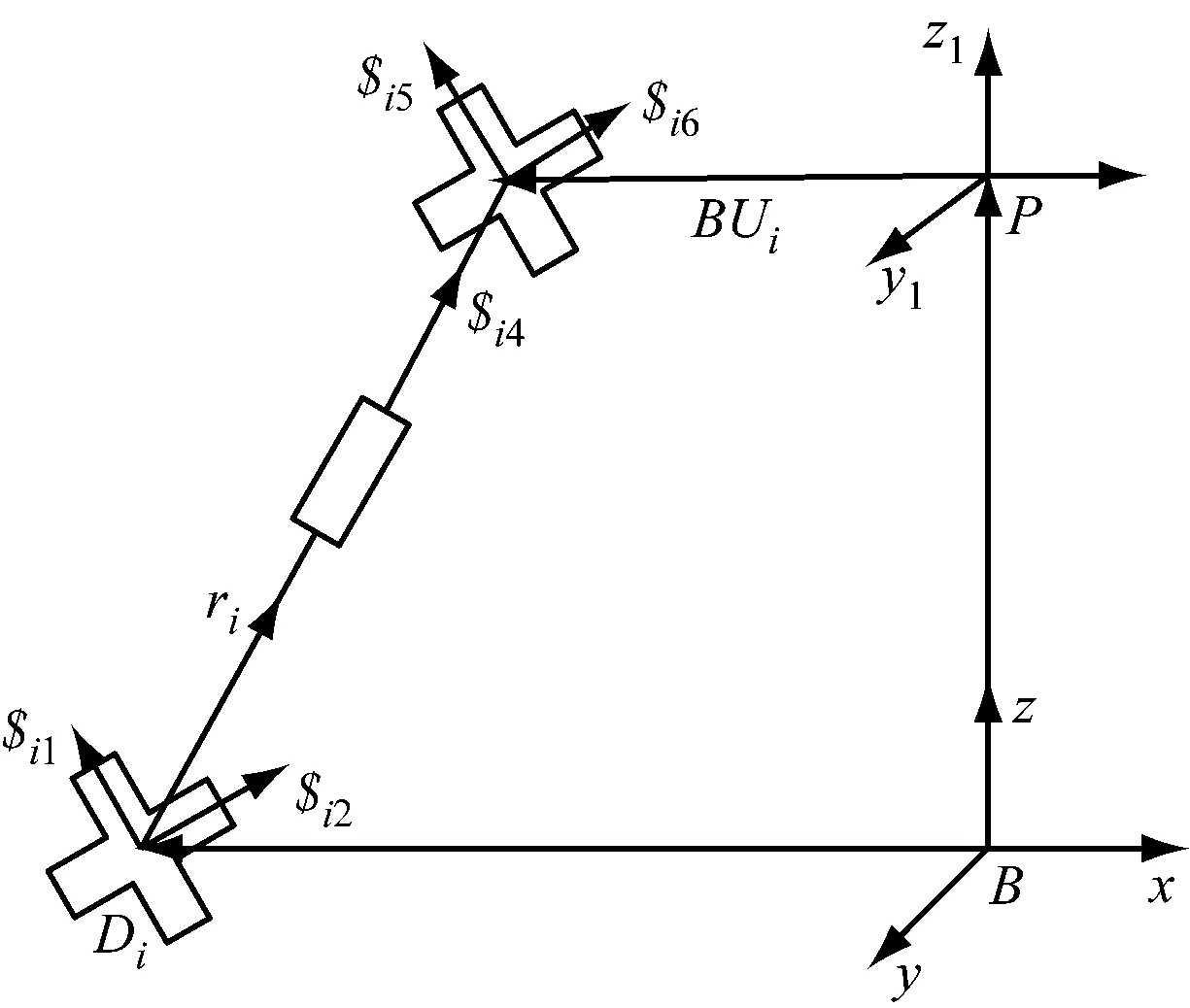
图2 支路等效图

由图2可知:每个支路都满足矢量方程

BDi+lini=BP+PUi

(4)

若已知点Di、点Ui、点P在固定坐标系中的坐标表示，通过联合式(2)、式(3)和式(4)可求出ni，从而确定旋转角度θi和δi，最后得到连杆在下平台的投影夹角。

1.3 运动学奇异分析

将与固定平台连接的下虎克铰分解为两个正交的螺旋$i1(i为机构的第i条支路,1为每个支路中的第1个单位运动螺旋)和$i2；圆柱副的运动可看作是移动副和旋转副，因此,把圆柱副分解为节距为无穷大和节距为零的两个单位运动螺旋$i3和$i4；将与运动平台连接的上虎克铰分解为两个正交的螺旋$i5和$i6。每个支路都可以等效为以上6个单位运动螺旋，其中:$i3的节距为无穷大，对应着主动副；其余的5个运动螺旋节距都为零，对应着被动副。任一支路中的6个运动螺旋对应的Plücker坐标分别为

(5)

由图2可知：沿x轴方向的虎克铰轴线与另一条虎克铰轴线和连杆都垂直，即

si1=si2×ri

(6)

若si2与ri共线，式(6)依然成立。因此,分两种情况讨论。

1)si2与ri共线，si6与ri不共线时

$i2=[001;000]

(7)

设si5=[mn0]

则si6=[-nmk]

(8)

得

(9)

因此，连杆DiUi的运动螺旋可表示为

$DiUi=[$i1$i2$i3$i4$i5$i6]

(10)

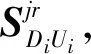
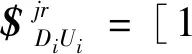
(11)

此时在第i个支路中存在着约束力螺旋通过Ui点，方向与固定在连杆上的下虎克铰轴线平行,见图3。

2)si2与ri不共线，si6与ri共线时

(12)

设si5=[mn0]

则$i5=[mn0;-nlml0]

(13)

此时得到

图3 支路中下虎克铰产生的奇异

(14)

在第i个支路中存在着约束力螺旋通过Di点，方向与固定在连杆上的上虎克铰轴线平行,见图4。

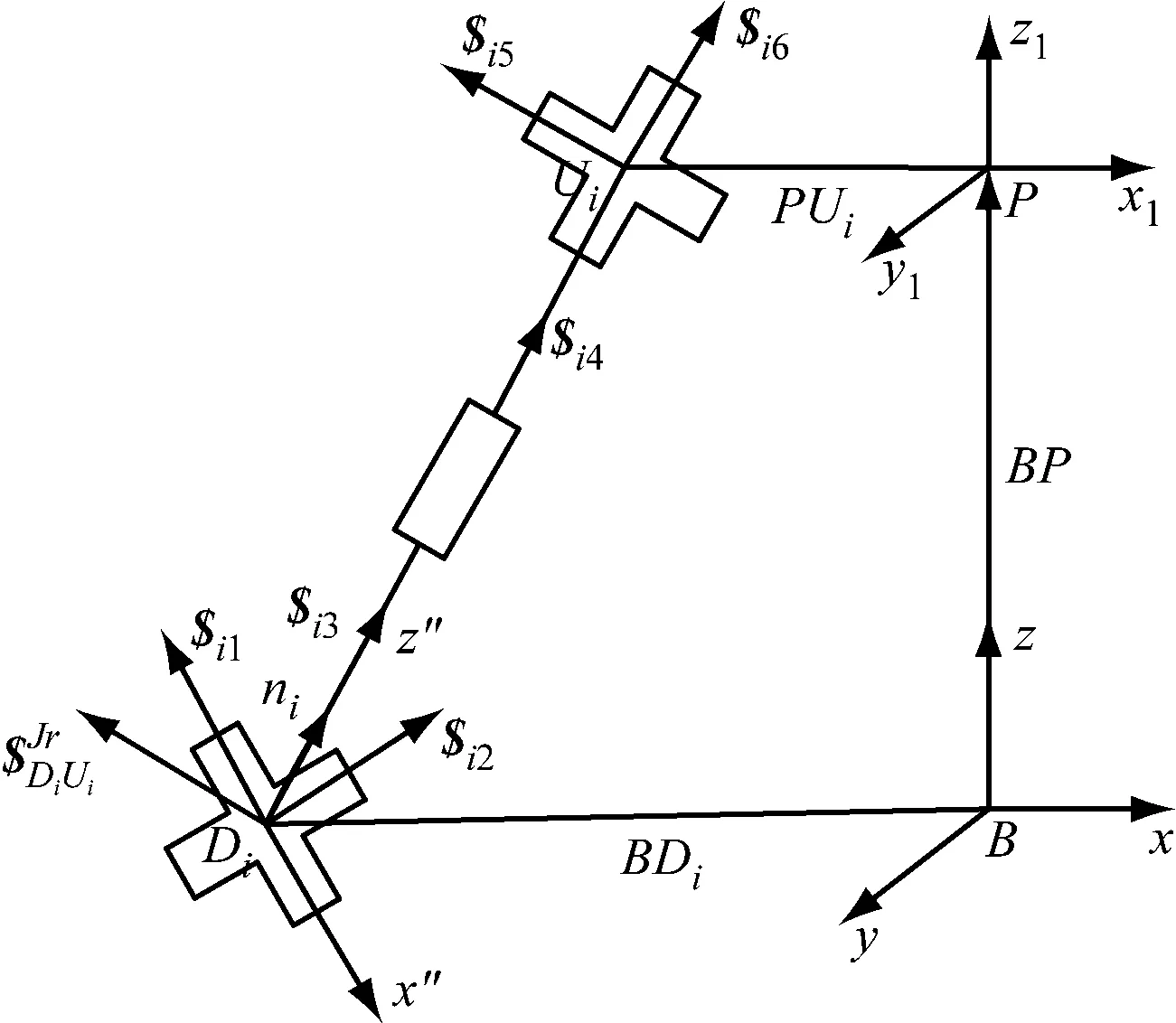
图4 支路中上虎克铰产生的奇异

将6条支路中的所有运动反螺旋合并成一个矢量空间为

(15)

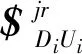
根据自由度的定义可得

rvs=6-cvs

(16)

由式(16)可知:当任意支路中存在反螺旋时，机构的自由度<6。因此,当作动器的轴线与下虎克铰的轴线共线，或者作动器的轴线与上虎克铰的轴线共线时，机构将会处于奇异姿态，称为运动学奇异。

1.4 约束奇异分析

前面用螺旋理论分析出被动虎克铰在支路中产生的运动学奇异，并得到平台产生奇异的两种情况。为了解平台产生约束奇异的条件，同样用螺旋理论对平台进行分析。

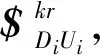
当约束住所有支路中的主动副时，如果施加外力矢，支路对动平台的约束力矢与外力矢抵消，平台处于平衡姿态，否则此时平台处于奇异姿态。

6个支路的反螺旋对动平台的约束力为

图5 支路中主动副产生的奇异

(17)

设外力矢量为

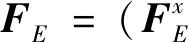
(18)

如果平台没有处于奇异姿态，则满足

(19)

由上述可知:局部坐标系是由固定坐标系Bxyz通过两次欧拉变换得来的，两次变换的欧拉角分别为θi和δi。支路i中的连杆在定平台的投影夹角为π/2-δi，投影线与定平台的y轴夹角为θi,如图5所示。

(20)

式(20)中：Δi=sinδi(xUcosθi-yUsinθi),i=1,2,…,6。当R(M)=6时，6个约束力线矢线性无关，能够充满整个机构的6维空间，根据机构的自由度理论可得到r=6-6=0，此时机构处于稳定姿态。然而当R(M)<6时，6个约束力线矢将会在机构空间变得线性相关，不能抵消掉来自外力的力线矢和力偶，此时机构处于奇异姿态，称为约束奇异。

2 基于遗传算法的奇异位形检测

当机构处于奇异位形时，自由度将会减少或增多，自由度减少会使机构达不到运行状态，自由度增加又会使机构变得不可控。因此，能快速找到或者检测到机构是否存在奇异显得尤为重要。如果知道机构在可达工作空间的运行轨迹，只需要检测在运行的过程中是否存在奇异位形。对于双端虎克铰的六自由度并联机构，需要同时考虑主动移动副和被动副对其产生的影响。上述分析得到运动学奇异和约束奇异两种机构奇异类型。当在可达工作空间内检测机构的奇异位形时，由于机构的作动器伸缩是非线性的，从而是一个非线性的寻优问题。由于遗传算法采用选择、交叉和变异算子进行搜索，全局搜索能力强，但是局部搜索能力较弱，一般只能得到问题的次优解，而不是最优解；经典非线性规划算法大多采用梯度下降的方法求解，局部搜索能力较强，但是全局搜索能力较弱。因此，本文结合两种算法的优点，一方面采用遗传算法进行全局搜索，另一方面采用非线性规划算法进行局部搜索，分别对机构产生的运动学奇异和约束奇异进行检测，以得到全局最优解。采用的非线性规划遗传算法的流程见图6。

图6 算法流程

2.1 基于非线性规划遗传算法的系统奇异位形检测法

2.1.1运动学奇异检测算法流程

经运动学奇异分析得到产生奇异有两种情况，分别是固定于下平台的虎克铰轴线与驱动器轴线共线和固定于上平台的虎克铰轴线与驱动器轴线共线，即si2与ri共线和si6与ri共线。为能快速找到平台在可达工作空间是否存在运动学奇异，只需检测si2与ri或si6与ri是否共线，也就是检测si2与ri的夹角或si6与ri的夹角是否为零。若已知固定于上、下平台虎克铰轴线的布局，si2与si6便可在空间进行表示。在一般情况下，固定在上平台上的虎克铰轴线和相应的窄边互相垂直，并与上平台平面呈45°；固定于下平台的虎克铰轴线与相应的窄边互相垂直和与下平台平面平行。假设上下平台的单位法向量分别为e1和e2，此时：

(21)

在机构的某一支路中，便可求出固定于上下平台的虎克铰轴线与连杆的夹角εi和μi，其中：

(22)

运用遗传算法对εi和μi的最小值进行寻优，算法流程如下：

(1) 编写一个用于计算min(εi,μi)的调用函数y=NonlinearFind(x)；

(2) 分别运用图6流程和遗传算法流程进行迭代寻优；

(3) 若寻优结果为零，说明机构在可达工作空间存在运动学奇异；若寻优结果>0，说明机构在可达工作空间不存在运动学奇异。

2.1.2约束奇异检测算法流程

对机构的约束奇异检测就是对矩阵M的行列式进行求解:如果|M|不为零，说明机构的6个运动反螺旋在空间线性不相关，机构不存在约束奇异;否则机构处于约束奇异姿态。运用遗传算法对|M|和-|M|的最小值进行寻优，算法流程如下：

(1) 编写一个用于计算(|M|min)和-(|M|min)的调用函数y=NonlinearFind(x)；

(2) 运用图6流程进行迭代寻优；

(3) 若寻优结果(|M|min)和-(|M|min)同号，说明机构在可达工作空间存在约束奇异；若寻优结果为(|M|min)和-(|M|min)异号，说明机构在可达工作空间不存在约束奇异。

2.2 算法实例

为验证提出的检测算法的有效性，对相关实例进行分析，并将结果与之对比。

采用BLAISE等[11]提出的5 000E伺服电动运行模拟机构，机构上下铰点的参数见表1。

表1中:U中的第i列代表上铰点Ui在局部坐标系P中的坐标;D中的第i列代表下铰点Di在惯性坐标系B中的坐标。

当机构处于中位时，局部坐标系P和惯性坐标系B重合，中位高度为1.176 9 m。

2.2.1运动学奇异实例检测

为避免算法运算结果具有局限性，对电动机构分别绕x、y、z轴转动、沿x、y、z轴平动和既转动又平动3种情况进行分析。

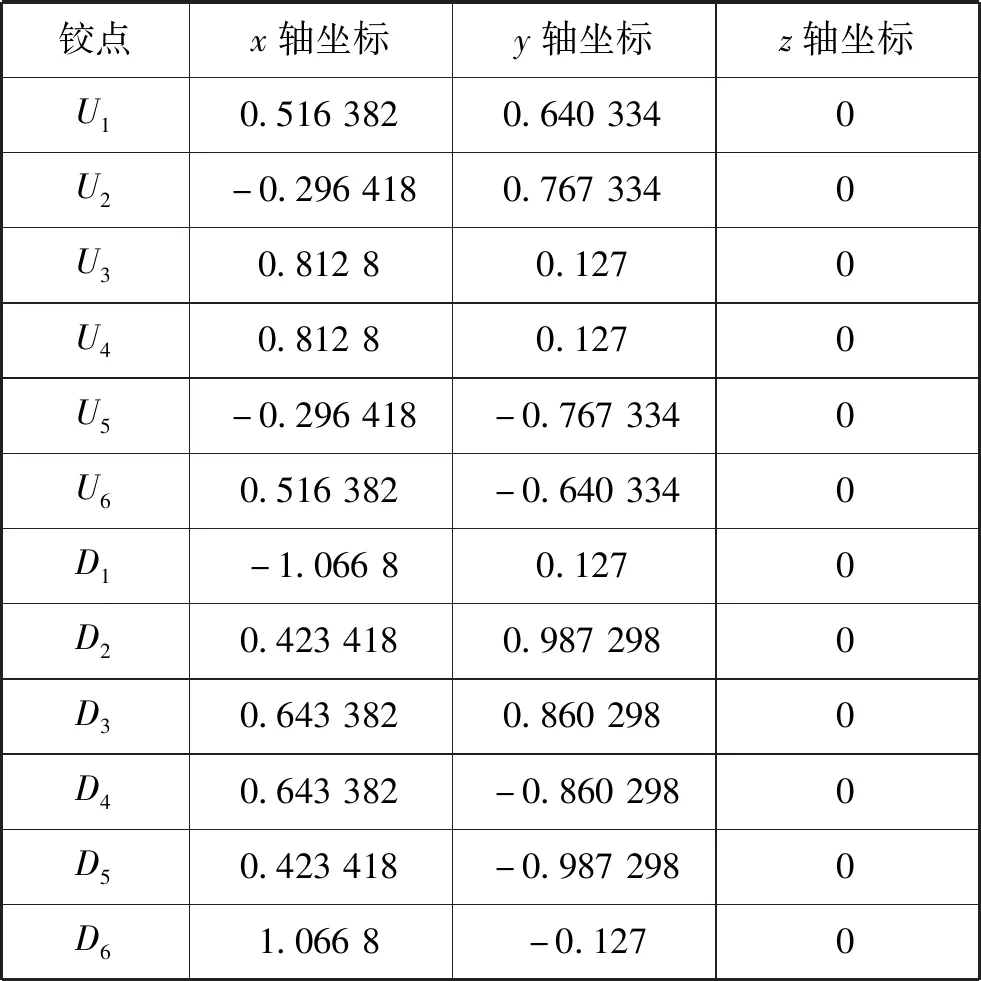
表1 上下铰点坐标参数

(1) 方案1:转动范围为(-18°,18°)、(-18°,18°)、(-20°,20°)。

(2) 方案2:平动范围为(-0.3 m,0.3 m)、(-0.3 m,0.3 m)、(-0.5 m,0.5 m)。

(3) 方案3:转动范围为(-18°,18°)、(-18°,18°)、(-20°,20°)；平动范围为(-0.3 m,0.3 m)、(-0.3 m,0.3 m)、(-0.5 m,0.5 m)。

所有算法都在MATLAB 2014a中完成，计算机的CPU是Inter(R)G630，主频为2.70 GHz，内存为4 GB，操作系统为Windows 7。基于非线性规划遗传算法和遗传算法的运动学奇异检测结果分别见图7和图8。如图7所示,进化2 000次后可知:方案1运行时间58.68 s，夹角最小值为29.42°；方案2运行时间52.36 s，夹角最小值为19.83°；方案3运行时间66.54 s，夹角最小值为34.31°。如图8所示，进化2 000次后可知:方案1运行时间52.17 s，夹角最小值为33.56°；方案2运行时间49.87 s，夹角最小值为27.48°；方案3运行时间58.88 s，夹角最小值为9.87°。所以,电动机构在可达工作空间不存在运动学奇异。比较图7与图8可知:在同等条件下，基于非线性规划遗传算法的收敛速度和求解结果上优于基本的遗传算法。可见，将线性规划方法同遗传算法相结合，提高了遗传算法的搜索性能。

2.2.2约束奇异实例检测

同样对电动机构的转动和平动进行约束奇异检测见图9。进化2 000次后可知:方案1运行时间102.35 s，(|M|min)=-0.496 7，-(|M|min)=0.392 6，(|M|min)与-(|M|min)异号，说明机构在方案1情况下不存在约束奇异；方案2运行时间113.24 s，(|M|min)=-0.535 6，-(|M|min)=0.282 5，(|M|min)与-(|M|min)异号，说明机构在方案2情况下不存在约束奇异；方案3运行时间121.54 s，(|M|min)=-0.347 2，-(|M|min)=0.212 3，(|M|min)与-(|M|min)异号，说明机构在方案3情况下不存在约束奇异。上述结果与BLAISE等人运用一种数值化方法进行奇异性检测结果一致，证明此算法的有效性。

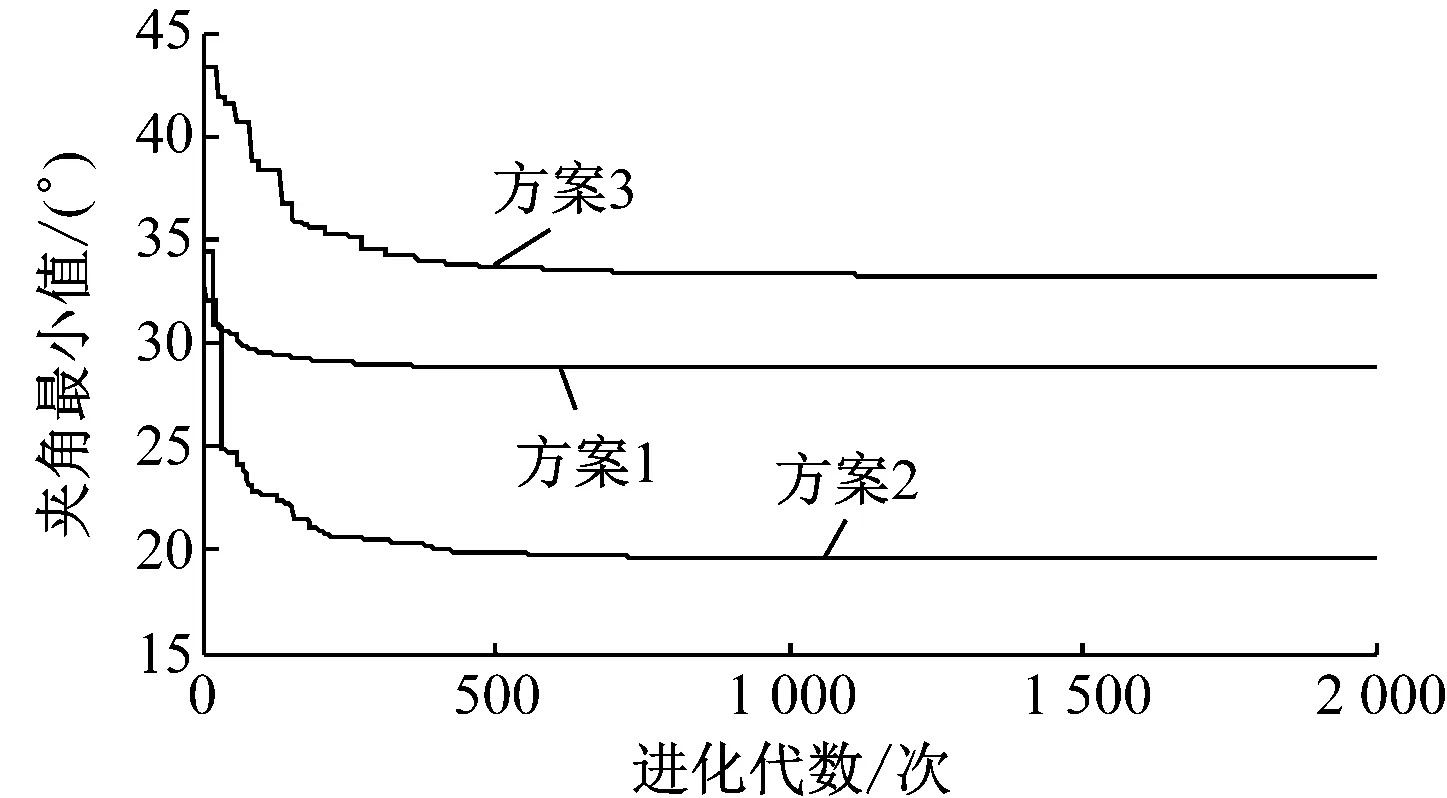
图7 基于非线性规划遗传算法的运动学奇异检测结果

图8 基于遗传算法的运动学奇异检测结果

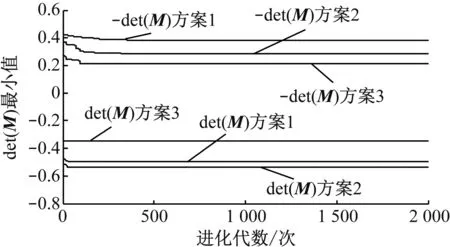
图9 约束奇异检测结果

2.3 算法实例二

同样为避免算法的局限性，采用一台有奇异位形的液压驱动六自由度运动模拟平台进行约束奇异检测。HUANG等[12]发现“对于六自由度运动模拟平台，当6个作动器的轴线都相交于同一条直线时，存在一个不需要的纯转动运动，即此时为奇异位姿”。为验证此平台是存在奇异位形的，采用所提出的约束奇异检测算法进行检测。液压机构上下铰点的参数见表2。

对液压机构分别绕x轴、y轴、z轴转动、沿x轴、y轴、z轴平动和既转动又平动3种情况进行分析。

表2 上下铰点坐标参数

(1) 方案1:转动范围为(-20°,20°)、(-20°,20°)、(-25°,25°)。

(2) 方案2:平动范围为(-0.5 m,0.5 m)、(-0.5 m,0.5 m)、(-0.35 m,0.35 m)。

(3) 方案3:转动范围为(-20°,20°)、(-20°,20°)、(-25°,25°)；平动范围为(-0.5 m,0.5 m)、(-0.5 m,0.5 m)、(-0.35 m,0.35 m)。

进化2 000次后可知:方案1运行时间115.32 s，(|M|min)=-0.702 8，-(|M|min)=-0.403 2，(|M|min)与-(|M|min)同号，说明机构在方案1情况下存在约束奇异；方案2运行时间109.6 s，(|M|min)=-0.280 3，-(|M|min)=-0.429 7，(|M|min)与-(|M|min)同号，说明机构在方案2情况下存在约束奇异；方案3运行时间131.49 s，(|M|min)=-0.653 2，-(|M|min)=-0.452 6，(|M|min)与-(|M|min)同号，说明机构在方案3情况下存在约束奇异见图10。此奇异性检测结论与实际情况相符，说明本文所提出的相应奇异性检测算法是可行的和有效的。

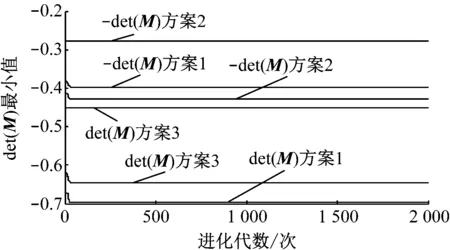
图10 约束奇异检测结果

3 结束语

通过运用螺旋理论分别对并联机构的被动副虎克铰和主动移动副进行奇异分析，得到机构产生两种奇异位形的条件。当固定于上下虎克铰的轴线与连杆的轴线共线时，机构处于运动学奇异，机构的自由度减少；当锁定各个支路的主动副，并且|M|=0时，机构处于约束奇异，机构的自由度增加。最后运用遗传算法对分析结果进行2 000次迭代寻优，检测结果证明此算法的有效性，最大运行时间为131.49 s，证明此算法的高效性，为以后船舶模拟平台实时控制过程中的奇异位形检测提供理论支撑。