双端虎克铰Hexaglide 并联机构零姿态工作空间分析
2020-11-23陈晓光李超锋焦胜海
陈晓光,李超锋,焦胜海,董 为
(1.北京航天长征飞行器研究所,北京 100076;2.哈尔滨工业大学机器人技术与系统国家重点实验室,黑龙江 哈尔滨 150080)
1 引言
根据并联机构的位姿特点[1],工作空间被分为位置工作空间、姿态工作空间、可达工作空间、灵活工作空间等。其中位置工作空间指在给定姿态情况下能够到达点的集合。
并联机构的工作空间求解比串联机构复杂,其求解方式有解析法和数值法,解析法的求解依赖位置解的研究。数值法则利用运动学逆解和结构约束进行搜索。在国内,文献[2]针对日本丰田公司的HexM 并联机床,以奇异位形等为限制条件,提出了一种计算工作空间的解析方法。文献[3]对3-TPT 并联机床利用虚拟样进行工作空间搜索。文献[4]考虑了虎克铰运动范围以及其对6-HTRT 并联机构工作空间的影响。在国外,文献[5]针对Stewart 平台,以支链长度和运动副摆角为约束,进行了工作空间搜索。文献[6]提出一种利用改进欧拉角表示并联机构姿态的离散搜索方法。文献[7]针对Stewart 平台,结合驱动元件长度、被动关节运动范围、支链干涉对工作空间进行了搜索。文献[8]利用关节转角限制、奇异点限制等因素搜索工作空间。
工作空间的求解,常将虎克铰近似为球铰。实际上,虎克铰运动范围比其等效球铰大,但安装后,受安装方式影响,部分工作空间未被计算。文献[9]提出利用虎克铰两个运动副同时可达摆角最大值作为约束虎克铰运动范围的准则。
2 研究对象介绍
2.1 研究对象及其坐标定义
研究的Hexaglide 并联机构用于模拟危化品运输车辆在各种工况下的位姿和速度,如图1 所示。由6 条长度固定的支链支承动平台,电机驱动丝杠带动滑块沿导轨运动。

图1 Hexaglide 并联运动模拟器Fig.1 The Hexaglide Parallel Mechanism
每条支链由与动平台连接的上虎克铰、与滑块连接的下虎克铰以及连杆组成,在下虎克铰一端有与连杆同轴的旋转副,上、下虎克铰尺寸相同。为进行逆运动学求解,建立的坐标系[10],如图2 所示。固定坐标系的XY 平面定义在与滑块连接虎克铰十字轴中心所构成的平面,X 轴垂直于导轨,Y 轴沿导轨。零位时动平台与定平台平行,动平台坐标系原点在与动平台连接虎克铰十字轴中心所构成六边形的中心。

图2 Hexaglide 并联机构运动及固定坐标系定义Fig.2 Definition of Motion and Fixed Coordinate System
2.2 Hexaglide 并联机构逆运动学求解
选用绕固定坐标系的RPY 角描述动平台的运动[10],为简化逆运动学求解,将支链的两端等效为两个中心分别位于支链虎克铰十字轴中心的球铰。与动平台相连的球铰Ai在全局坐标系下的位置可以用如下齐次变换矩阵表示:


与滑块相连的球铰Bi的位置可以表示为:

支链长度固定,滑块的位移通过求解式(5)的六个方程:

求得各滑块位移如下:
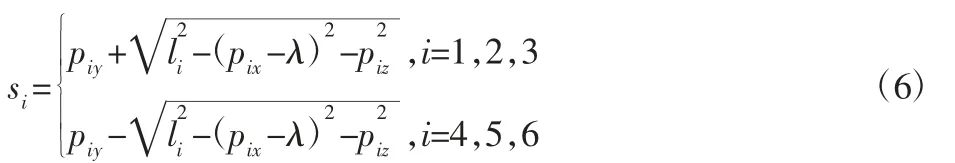
3 虎克铰对工作空间影响分析
虎克铰是否干涉是并联机构工作空间重要的约束,也是这里的创新点之一。因虎克铰的干涉与安装方式和位姿相关,以下首先对干涉形式进行分类,再对其自由状态下的运动范围进行分析,最后求解虎克铰装入并联机构后的摆角。
3.1 虎克铰运动描述
为描述虎克铰的运动,固定虎克铰的一个分支,建立坐标系,如图3 所示。在下方的虎克铰建立固定坐标系O-xyz,在上方虎克铰建立运动坐标系O-x′y′z′。两个坐标系的x 轴重合,均沿着与固定分支连接旋转副的轴线。运动分支坐标系的z′沿着支链的方向,固定坐标系的z轴从十字轴中心指向固定部分连接法兰的中心。两个坐标系原点相互重合,位于虎克铰十字轴中心。

图3 描述虎克铰运动所建立的坐标系Fig.3 Coordinate System for Describing Hooke Joints’Motion
在图3 所示的坐标系中,虎克铰的运动可以描述如下:
首先绕固定坐标系x 轴转动α,再绕新位置坐标系的y′轴转动β。利用坐标变换在同一个坐标中描述两个分支曲线方程。坐标转换矩阵如下:

3.2 虎克铰干涉情况分析
利用3.1 节描述的虎克铰运动,在不同的α、β 转角情况下,所研究虎克铰的干涉情况,如图4~图6 所示。假设上部带有法兰的分支是固定的,与之相配合的另一部分是运动的。发生干涉的情况分别是:运动虎克铰分支的侧棱面与固定分支连接法兰干涉、运动虎克铰分支的外棱线与固定分支的圆弧过渡段干涉以及虎克铰两分支的内棱发生干涉。

图4 运动分支外棱线与固定分支连接法兰干涉Fig.4 Interference Between the Outer Ridge of the Moving Branch and the Fixed Branch Connecting Flange

图5 运动分支外棱线与固定分支圆弧过渡处干涉Fig.5 Interference Between the Outer Line of a Moving Branch and the Circular Transition of a Fixed Branch

图6 虎克铰两分支内棱线干涉Fig.6 The Inner Edge Interference of the Two Branch
在三维软件中拖动虎克铰运动可以发现,随α 角的增大,β角的极限值逐渐减小。据此以α 为自变量,以发生干涉时的β 的极限值为因变量,得到虎克铰的运动范围。
通过对图4~图6 进行分析,发生干涉的临界条件是相互配合的虎克铰两个分支的某两条空间曲线(通常是空间直线或者圆弧)相交。因此通过干涉时两相交空间曲线方程联立就可以计算干涉时两分支摆角,最终能够得到虎克铰的运动范围。涉及的各支链的上、下虎克铰尺寸是相同的,且每个虎克铰的两部分尺寸也是相同的,因此虎克铰的运动范围具有高度的对称的,只需考虑当α 和β 均为正的情形,由对称性即可得虎克铰的运动范围α-β 图。
3.3 虎克铰运动范围求解
虎克铰两分支干涉的临界状态是两条空间曲线相交。临界干涉且当虎克铰两摆角α、β 均为正时,虎克铰两分支的干涉部分,如图7 所示。图7 左侧为虎克铰的固定分支,临界干涉状态时相交的空间曲线是圆弧段AB 与直线段BC,右侧为虎克铰的运动分支,临界干涉状态时相交的空间曲线是内棱侧线段DE 和外棱侧线段FG。当虎克铰的两个分支绕十字轴旋转不同角度α 与β 时,上述空间曲线的不同部分相交。计算过程中涉及到的虎克铰分支的尺寸,如图8 所示。

图7 摆角均为正时固定虎克铰分支干涉棱线Fig.7 Interference Lines of Fixed & Moving Hooke Joint when the Revolution Angle is Positive

图8 虎克铰运动范围计算所需尺寸Fig.8 The Required Size for Calculating the Motion Range of Hooke Joints
固定分支的过渡圆弧与内棱直线方程可以表示如下:

式中:x、y、z—图4 建立的固定坐标系的坐标值;w—虎克铰某一分支两内棱间距,即为虎克铰宽度;θ—圆弧参数方程的极角,范围为[0,π/2]。
为求得空间两曲线交点,需要在同一坐标系下联立两个分支相交曲线的方程。运动虎克铰分支的干涉段为两直线,以运动分支内棱在固定坐标系下的方程为例,在运动分支内棱取两点X1、X2。经坐标变换成为固定分支坐标系中的点(α,β)=RX2。利用空间解析几何知识,运动分支内棱在固定分支坐标系的方程为:
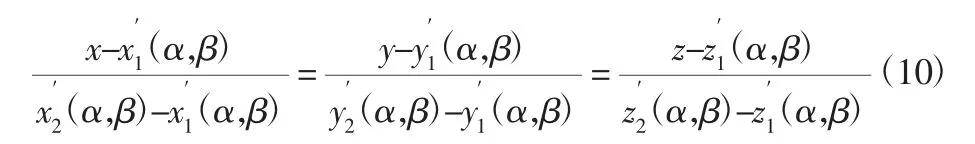
虎克铰运动分支外棱在固定坐标系的方程求法类似。
联立干涉临界状态时相交的空间曲线方程,即可得到如图3所示坐标系中转角α 和转角β,即虎克铰摆角状态。需计算的分界点及极限点有:(1) 图 4 的情况为分界点 1 对应摆角 α1;(2)图4 与图 5 的分界点为分界点 2,对应摆角 α2;(3)图 5 与图 6 的分界点为分界点3,对应摆角α3;(4)α4为结构对称导致的对称分界点。在固定虎克铰某一分支时两旋转副的约束关系,如图9 所示。该图有高度对称性,是由于虎克铰分支尺寸相同导致的。

图9 虎克铰运动范围图Fig.9 Motion Range Map of Hooke Joints
3.4 任意位姿下虎克铰转角计算
在3.3 节建立了虎克铰分支转角的约束关系。Hexaglide 并联机构每条支链的两个虎克铰分别与动平台和滑块连接,只有求解出某一位姿下12 个虎克铰的摆角,才能利用图9 判别该位姿是否发生干涉。典型虎克铰摆角状态,如图1 所示。
动平台处于某一位姿时,12 个虎克铰摆角的计算,是通过两种不同的途径计算同一支链与滑块(或动平台)固连的另一端虎克铰中心点坐标,并联立这两种计算途径方程实现。以与动平台连接的虎克铰摆角为例,两种途径是:
在图3 中的坐标系Σo-xyz,经坐标变换:


判别虎克铰摆角是否在运动范围的判断子程序流程,如图10 所示。Jointflag=1 表示虎克铰不干涉,Jointflag=0 时干涉。

图10 虎克铰干涉情况判断子程序框图Fig.10 Block Diagram of the Subprogram of Hooke Joints Interference
4 限制并联机构工作空间的其他因素
对所研究的Hexaglide 并联机构,选用了零姿态下的位置工作空间进行可视化的搜索:指定并联机构的3 个姿态,在一定的位置空间内利用逆解以及结构约束进行搜索。若某一点在工作空间内,那么它一定满足逆解、结构参数等约束。
除虎克铰的运动范围约束外,搜索Hexaglide 的工作空间还需要以下限制条件:
4.1 导轨长度的限制
Hexaglide 并联机构的滑块沿着导轨运动,搜索空间不能超出导轨的长度范围。在满足功能需求的前提下,为缩小搜索范围,仅对导轨中间区域搜索,导轨两端的区域不搜索。
4.2 相邻杆件的干涉限制
相邻两支链连杆不干涉,体现在数学描述上为两条异面直线间距大于连杆直径。对Hexaglide 并联机构而言,发生干涉的只能是相邻支链的连杆。异面直线距离的公式为:

式中:d(l1,l2)—两连杆异面轴线间距—连杆 1 的方向向量—连杆 2 的方向向量—两支链连杆上两点连线的方向向量。
4.3 同支链上下虎克铰中心相对位置限制
文献[11]中,提出了动平台虎克铰十字轴中心在同一支链滑块虎克铰十字轴中心内侧的限制,以避免奇异位姿。
5 零姿态工作空间计算及验证
5.1 零姿态工作空间计算
综合前文中建立的约束,结合运动学逆解,在零姿态情况下对位置工作空间进行了极坐标形式的搜索。得到的零姿态位置工作空间,如图11 所示。
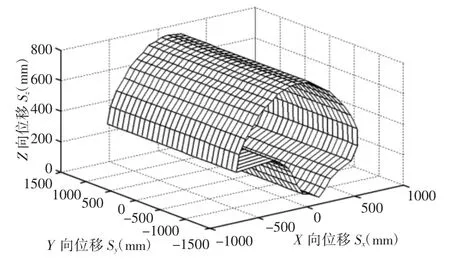
图11 双端虎克铰Hexaglide 并联机构零姿态工作空间Fig.11 Zero Orientation Workspace of the Hexaglide Parallel Mechanism with Hooke Joints
与基于虎克铰的工作空间对比,搜索了基于球铰的工作空间:将每条支链的虎克铰换为球铰,球铰的运动范围视虎克铰运动范围图的最大内切圆,如图9 所示。得到的基于球铰的零姿态工作空间,如图12 所示。二者的截面对比,如图13 所示。

图12 双球铰Hexaglide 并联机构零姿态工作空间Fig.12 Zero Orientation Workspace of the Hexaglide Parallel Mechanism with Spherical Joints
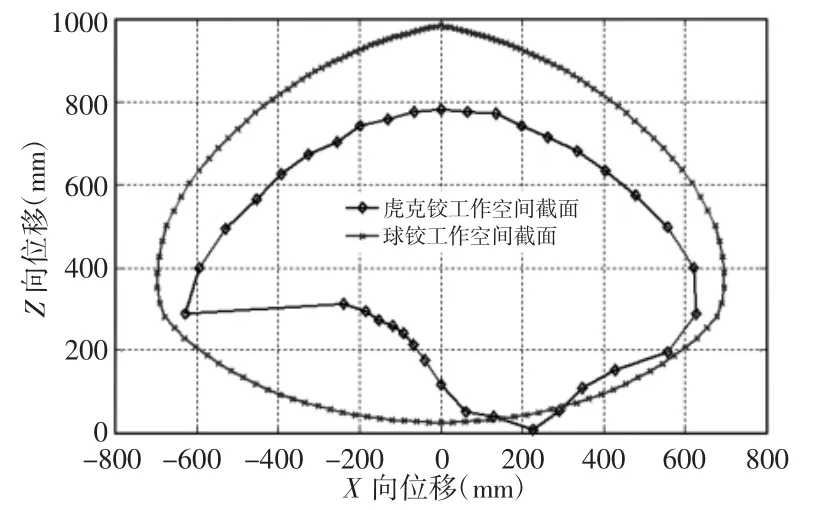
图13 不同运动副对应的工作空间截面对比Fig.13 Workspace Comparison Between Different Joints
5.2 基于虎克铰与基于球铰零姿态工作空间验证
通过图13 的对比,基于球铰的工作空间比基于虎克铰的工作空间大,似乎与单个虎克铰的运动范围比球铰的大相矛盾。这是因为,安装在并联机构上的虎克铰的运动范围除与自身尺寸相关外,还与安装角度有关。点[-200,0,+200]在差集中,在三维软件中施加约束,观察干涉情况,证明该点的确在工作空间外。发生了虎克铰干涉,如图14 所示。
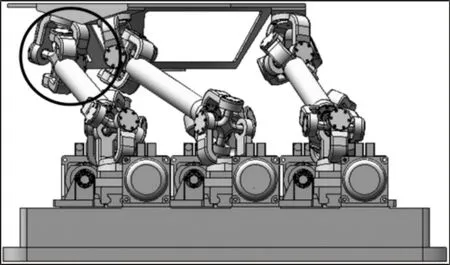
图14 基于虎克铰运动范围的工作空间三维模型验证Fig.14 Three Dimensional Model Validation of Workspace Based on Hooke Joints’Motion Range
第4 支链动虎克铰摆角干涉,如图15 所示。在运动范围外。

图15 图14 所示位姿下第4 支链虎克铰摆角位置Fig.15 Hooke Joints Position of the Fourth Chain Under the Pose Shown in Figure 14
6 结论
建立虎克铰运动范围模型,利用虎克铰两个旋转副的转角描述虎克铰运动范围,同时提出了任意位姿下虎克铰两旋转副的转角求解方法。为虎克铰是否干涉提供判据。
利用运动学逆解,结合虎克铰运动范围、导轨长度限制、相邻支链干涉约束和同支链虎克铰中心相对位置限制,对Hexaglide 并联机构的零姿态工作空间进行搜索,得到了精确的零姿态工作空间。通过与基于球铰计算得到的结果对比,验证了虎克铰安装方式影响工作空间的结论。
受限于计算资源,仅对零姿态下的位置工作空间进行了搜索。实际上,固定任意3 个自由度,都能得到其他3 个自由度的工作空间。相关研究成果对双端虎克铰并联机构工作空间的精确搜索有着较好的指导意义。
出于满足功能需求考虑,仅对导轨中间的工作空间进行了搜索,导轨边界附近的工作空间有待进一步研究。
