手工地毯植绒机轨迹规划及其速度控制优化

周 虎， 刘涛， 高金杰， 周 强， 罗滨鸿， 游 政， 苏炳望， 巴 拉

(东华大学 机械工程学院， 上海 201620)

手工地毯是一种高档地面铺装材料，展览厅、酒店、会馆等高档场所，以及家居等对手工地毯的需求量居高不下[1-2]。由于传统手工地毯生产方式周期长、成本高、劳动强度大，加工过程不利于环保等缺点，不少企业开始研发和应用自动枪刺植绒机器人生产手工地毯。自动枪刺植绒机采用机械手代替人工扎毯动作，利用多个伺服轴的联动实现轨迹控制，达到在基布上生成簇绒图案的目的[3-4]。由于栽绒机器是一个复杂的四轴联动机构组成,加工过程中针头和基布互相干涉耦合，加工路径变化剧烈处产生机械振动和基布相对偏移和变形，导致针头在实际基布的位置发生变化，呈现在实际产品上就是相邻色块存在重叠或偏离，严重时出现破洞等问题。为了在较高加工速度下实现高品质的毯面质量，从分析手工地毯植绒机器的机电系统结构着手，研究植绒加工过程中相对路径偏移产生的根源，从而采用相应的机器人轨迹规划和速度优化控制策略，以期提升手工地毯加工品质，实现机器人最终工程化应用。

1 机电系统架构

为实现植绒执行机构在基布平面的定位，设计了机器人整体机械架构以及植绒执行机构如图1所示。其中X轴和Y轴由丝杆驱动，实现植绒头的平面坐标定位。植绒执行机构由传统枪刺机械改造，Z轴伺服电动机驱动曲柄滑块机构，带动针头往复运动实现植绒动作；W轴伺服轴可连续正反旋转，实现针头始终保持与加工路径的相切。4个轴的配合联动可实现任意簇绒图案的加工。

基于以上机械系统架构，采用CAD/CAM技术，根据设计师图案，实现在基布上自动生成簇绒图案。系统对预先设计的图案进行处理生成适合运动控制装置执行的指令集，并自动控制编织动作，采用专业的运动控制算法，实现刺枪的高精度和高速定位，代替人工编织割绒和圈绒。监控计算机完成图案的解析并转换成植绒头的运动轨迹，通过网络实现与运动控制器的实时通信，控制四轴联动完成植绒运动并检测纱线和人机交互等状态信号,机电系统结构如图2所示。

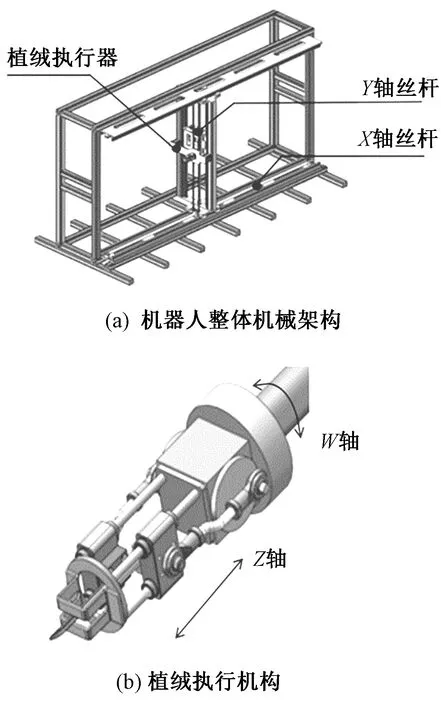
图1 机械结构示意图

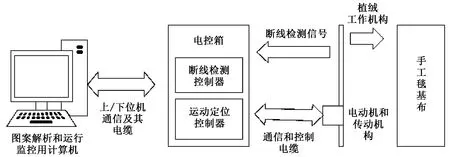
图2 机电系统结构

2 运动关系分析与速度优化控制

2.1 运动关系分析

设植绒针迹点集合定义为(P1,P2,P3,…，Pi-1,Pi,Pi+1，…)，如图3所示。X、Y、Z、W四轴运动关系可根据3相邻特征点Pi-1(Xi-1,Yi-1),Pi(Xi,Yi),Pi+1(Xi+1,Yi+1) 来说明。

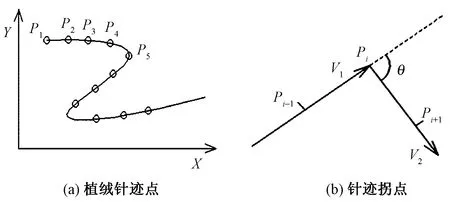
图3 针迹点示意图

从点Pi到Pi+1，X轴和Y轴的距离增量分别为ΔX=Xi+1-Xi,ΔY=Yi+1-Yi, 很容易计算2点之间的距离Li；由于针距恒定，Z轴的运动增量ΔZi=K×Li(K是根据针距计算出的Z轴和XY插补轴的电子齿轮比)；W轴的姿态必须保持与工作路径相切，由于相邻3点坐标已知，可计算得Pi-1→Pi的角度θi-1, 以及Pi→Pi+1的角度，则ΔWi=θi-θi-1.至此建立了四轴联动关系。

2.2 速度优化控制

轮廓跟随误差是伺服驱动插补器输出的位置设定值，与位置测量系统(伺服电机编码器) 或检测的位置实际值之间的误差。跟随误差主要与加工速度变化有关，特别是加工曲线轮廓，因联动轴的加减速不同步，引起轮廓误差。当植绒机器以一定的作业速度扎毯时，根据ε=v/Kv(Kv为进给轴的伺服增益)，跟随误差ε与进给矢量速度v成正比[5-9]。在稳速直线运动过程中，跟随误差不应发生波动，否则将造成轮廓误差。

以两轴联动加工直线轮廓为例，如图4(a)所示产生的轮廓误差为

ε=[(kvX-kvY)vsin2θ]/2kvxkvy

(1)

式中:v为直线加工进给速度， mm/s；θ为直线与X轴的夹角，(°)；kvX和kvY分别为X、Y轴的位置环增益。由式(1)可得，在直线加工时，当kvX=kvY时，直线轮廓误差为0。

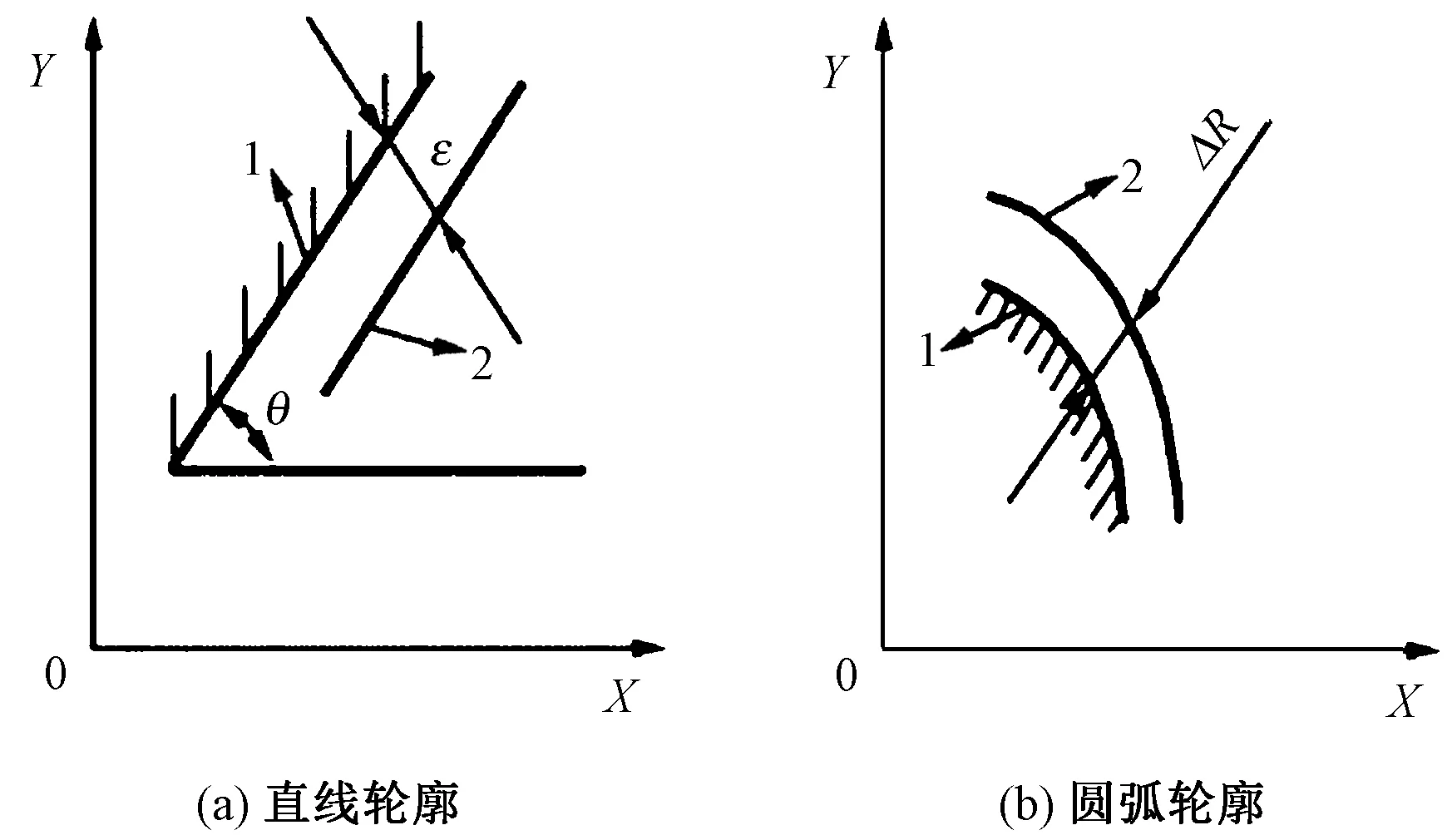
图4 加工误差示例

X、Y轴联动加工圆弧轮廓时，如图4(b)所示，产生的轮廓误差为

ΔR=vR/2kvxkvyR

(2)

式中：vR为圆弧加工进给速度；R为圆弧半径。图中1表示理论轮廓，2表示实际轮廓。

(3)

假设速率v1和v2的绝对值大小不变，即v1=v2=v，进一步计算可得机械手在加工过程中受到的冲击力为

(4)

由式(4)可知，在保持恒定的加工速率下，机械手受到的冲击力的大小主要取决于XY运动路径的拐点夹角，即拐角越大，受振动冲击力越大。当然，Z轴高频往复运动同样会带来机械冲击，但由于冲击主要在Z轴方向，不会对扎毯路径造成偏移影响，故可忽略不计。

当遇到拐角而不减速时，容易扎烂毯面，严重时会出现破洞。要减小机械手在加工拐点处的冲击力，就必须要增大时间，即要减小加工速度，特别是在拐点夹角比较大时。为取得较高的加工效率，同时保证良好的加工品质，本文提出了一种自适应速度控制策略，即根据路径特征点的角度变化，自动调整矢量速率[10]。本文控制系统中，机械手的运行速度V与针迹点轨迹变化夹角θ之间的关系如图5所示，采用单边高斯函数逼近方法来建立关系方程。

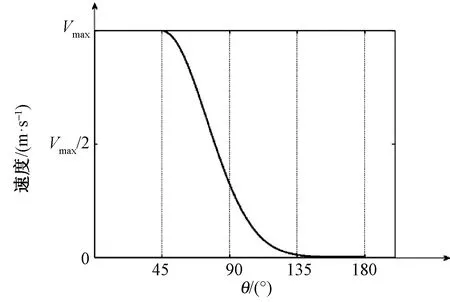
图5 速度自适应曲线

在0°≤|θ|≤45°范围时，由于夹角变化不多，运动轨迹较为平缓，机械手可近乎最高速度加工；在45°<|θ|≤135°范围时，拐点夹角大，为保证运行平稳，加工速度需急剧减小；135°<|θ|≤180°范围时，拐角过大，机械手需以非常小的速度通过拐点。机械最高运行速度设定为2 000 r/min，得到：

(5)

这样机器人在加工任意曲线时，都能以合理的速度和加速度进行加工，实现加工速度的自适应控制。

3 轨迹规划器设计

手工地毯枪刺植绒机器人是多轴的机电一体化设备，只有当机器人的各轴沿着预定路径协调运动时，由计算机程序编制的枪刺植绒作业才能顺利完成，因此，机械手运动轨迹规划及控制是实现高性能簇绒的重要条件。

为控制植绒执行机构能沿任意直线或曲线运动，必须同时控制每一个轴的位置和速度，使他们同步协调到达目的地。采用三次多项式样条函数轨迹规划器实现对速度和加速度控制的多轴机械手，以生成复杂的运动轨迹[11、12]。

假设1条连续的空间轨迹，由时刻t0至tf分成N段。每一段用三次多项式样条函数逼近，相邻两边界连接点上的轨迹保持连续。根据第2节分析，已经获取了每一段两端点的坐标位置和速度。

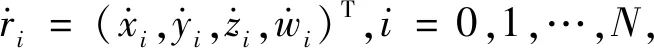
(6)

将通过i-1和i点的三次多项式样条函数表示为

r(τ)=a1+a2τ+a3τ2+a4τ3

(7)

对τ求一次微分：

(8)

显然，边界条件为:

将这些边界条件代入式(7)和(8)，解上述联立方程，可求得三次多项式样条函数的4个待定系数a1、a2、a3及a4:

a1=ri-1

将这些系数带入式(7)，可得到三次多项式样条函数表达式为：

(9)

或者：

(10)

由三次多项式样条函数确定的轨迹，在相邻2段之间是平滑的，不仅路径连续，而且一阶导数(速度)也连续，这正好可以保证枪刺植绒机器人作业时所需要的优良性能。

假设栽绒机器人某轴在5 s时间内从初始角 30°运动到75°，利用上述轨迹规划器所生成的位移、速度和加速度曲线，如图6所示。

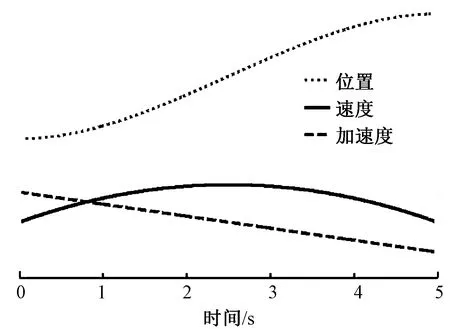
图6 机器人位移、速度及加速度曲线

4 实验讨论

4.1 实验装置

根据上述讨论开发了适用于手工地毯枪刺作业的自动植绒机器人，图7示出正在车间作业的设备现场场景。

关键控制部件：采用工控机进行路径和轨迹计算，运用GALIL DMC-1842型运动控制器对四伺服轴进行插补控制，伺服驱动采用台达ASDA-AB系列。

图7 手工地毯植绒机运行场景

4.2 实验方法

根据曲线路径点序列，计算得到各采样小段中的4个轴的运动增量脉冲和运动时的首尾瞬时速度，得到手工地毯植绒机加工中的关键程序。

分别用恒定速率和基于三次多项式样条函数的轨迹规划器进行植绒加工作业，观察装备在加工过程中的稳定性和手工地毯的加工品质。

4.3 实验结果

图8示出手工地毯设计路径图。当采用较高的恒定速率加工时，可明显发现扎毯线条的拐点处设备振动剧烈，作业路径偏离原设路(相邻颜色出现偏离或重叠)，大拐点处加工毯面出现烂布现象。图9示出实际扎毯过程中出现的明显路径偏移，实测最大路径偏移量达5.8 mm，造成废品而不得不中断生产。

图8 地毯设计路径图

图9 扎毯过程路径偏移图

针对该问题，应用本文提出的根据拐点转角大小的速度自适应控制策略，以及三次样条函数轨迹规划器实现多轴系统的协调运动控制方法。在该控制策略下，加工作业速度随曲线路径的变化而自适应调整，明显缓解了加速度突变引起的机械冲击。图10示出采用三次样条曲线对多轴插补运动速度进行优化控制得到的加工后效果图。可以看出，图中针迹点均匀，行距最大路径偏移仅0.6 mm，达到了满意的效果，从图中可以看出毯面质量有了实质性的改进。

图10 优化控制策略下的加工毯面效果

5 结束语

为了在较高的加工速度下加工高品质的毯面，本文分析了手工地毯植绒机器四轴联动的机电系统结构，得到了各运动轴的连续联动控制方式与路径特征点序列的关系。通过研究植绒加工过程中相对路径偏移产生的根源，发现了机械手在加工作业中的所受冲击力取决于路径拐点处的转角大小，从而提出了采用速度自适应控制策略，即在不同拐角点采用不同的作业速度，既保证了加工效率，又可缓解因矢量速度和加速度频繁变化引起的机械震动和冲击。最后本文采用基于三次多项式样条函数的轨迹规划器实现多轴系统的协调运动控制，对加速度和速度受控的多轴机械生成复杂的运动轨迹，实现平滑运动，有效提升了加工的毯面质量。