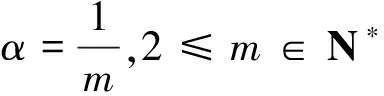一个无理分式不等式猜想的证明

浙江湖州市双林中学 (邮编：313012)

《数学通报》2016年9月号问题2325[1]：

设x、y是满足xy=1的正数，λ≥0，求证：

文[2]从项数入手，给出了上述不等式的“元”推广：

①

故而文[2]改从指数入手，给出问题2325的指数推广为：

设x、y>0,xy=1,2≤m∈N*,λ≥0，则

②

基于①、②二式，文[2]末作者自然提出如下靓丽的猜想：

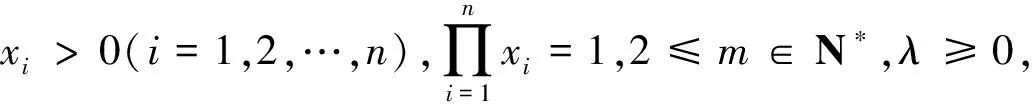
③

这是集问题2325指数推广与“元”推广于一体的综合性推广，是一个很有意义的不等式之“梦”. 几经思考、几经挫折，终得以修成正果. 下面给出猜想的证明.

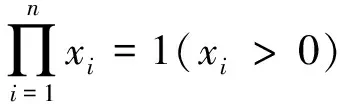
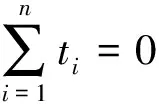
④

并作辅助函数：

易知猜想等价于以下不等式：

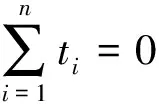
③′

为此，考察函数f(t)的凹凸性，即f″(t)的符号，可得：

⑤

>0(因m≥2).

所以，函数f(t)在(-∞,+∞)内是下凹函数，故而

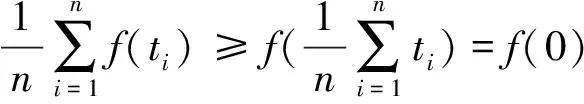
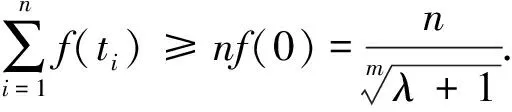
③′式成立，即③式成立. 猜想得证.

从以上猜想的证明过程⑤式，易知：

λ2(m-1)2e2t+λm(2m-3)et+m2

≥λm(2m-3)et+2·λ(m-1)et·m

=λm(4m-5)et,

⑥