一种十字阵列模型下的新型测向算法

蒋 驰，王耀金，王 昭，王 帅，徐 强

(上海无线电设备研究所，上海 201109)

0 引言

随着导引头精度和实时性的要求越来越高，适用于导引头测向的传统算法受到了严峻的挑战。经典的干涉仪测向算法[1-2]凭借着其高实时性受到了广泛的关注和应用。该算法利用2根天线之间的相位差进行测向，原理简单，计算量小，硬件可实现性强，但存在无法实时处理多目标、精度偏低等问题。为此，在测向实时性允许范围内引入阵列思想，通过空间分散排列的传感器阵列和多通道接收获取信号的时域、空域等多维信息，同时配合一系列空间谱估计算法来检测信号和提取参数，具有灵活、信号增益高、抗干扰能力强、空间分辨能力强等优点[3]。经典的空间谱估计方法主要包括多重信号分类(MUSIC)方法[4-6]、Capon算法[7-8]、信号参数估计算法(ESPRIT)[9-10]、传播算子算法(PM)[11-12]等。

传统的PM算法是利用天线阵列接收信号来构造传播算子，通过传播算子的旋转不变特性配合特征值分解来进行二维测向，其只适用于均匀分布的阵列。二维PM算法利用传播算子构造了二维空间谱函数，并通过二维方向上的谱峰搜索来测向，该算法测向精准但牺牲了单次测向时间[13-14]。

本文提出了一种正交的PM测向算法，引入了噪声子空间的投影算子构造伪谱，并采用一维谱峰搜索实现二维测向，相比二维PM算法减少了计算量，降低计算复杂度。该算法既可以多目标测向，又可以解决角度配对的问题，还可有效地估计出相同方位角(或仰角)的目标。考虑到天线阵列在空间位置上的合理排布，因此，将该算法配合使用在十字阵列中。

1 数据模型

十字型阵列的阵元结构如图1所示。由图可见，阵元均匀分布共有2M-1个。其中相邻阵元间距是d=λ/2，λ为信号波长。考虑到远场信号，信源足够远，信号到达阵列时可以认为是平行波。假设噪声与信号独立，且是加性独立同分布的高斯过程。假设有K个非相干信源，第k个信源对应的仰角和方位角分别表示为θk和φk，定义uk=sinφksinθk，vk=cosφksinθk，则X轴上M个阵元接收的信号可表示为

Xx(t)=AxS(t)+Nx(t)

(1)

式中：Ax=[ax(v1),ax(v2),…,ax(vK)]，ax(vk)=[ejπ(M-1)dvk/λ,…,ej2πdvk/λ,1,e-j2πdvk/λ,…,e-jπ(M-1)dvk/λ]T，其中[·]T表示转置；Nx(t)为X轴上子阵的加性高斯白噪声；S(t)∈CK×1为信源矢量。

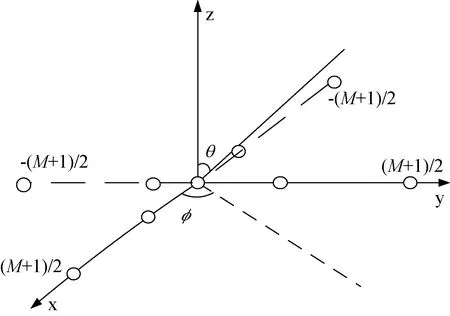
图1 十字阵列的阵元结构Fig.1 Structure of the cross array

类似地，Y轴上M个阵元接收的信号可表示为

Xy(t)=AyS(t)+Ny(t)

(2)

其中：Ay=[ay(u1),ay(u2),…,ay(uK)]，且ay(uk)=[ejπ(M-1)duk/λ,…,ej2πduk/λ,1,e-j2πduk/λ,…,e-jπ(M-1)duk/λ]T；Ay为Vandermonde矩阵；Ny(t)为Y轴上子阵的加性高斯白噪声。

十字阵列的接收信号可表示为

(3)

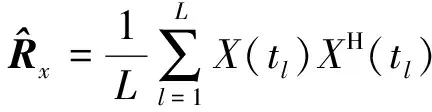
2 正交PM测向算法

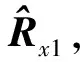
(4)

构造的矩阵

(5)

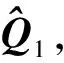
(6)

根据定义构造伪空间谱函数为

(7)

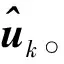
(8)

(9)

(10)

测向算法的具体步骤为：

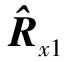
测向算法具有以下特点：一是可实现多目标的测向，并且实现二维角度的自动配对；二是一维搜索只需做2次，避免了二维搜索庞大的计算量；三是由于搜索的直接对象是u和v，因此可有效估计出相同方位角(或仰角)的目标。

3 仿真验证

3.1 可行性仿真

3.1.1 多目标源测向

图2是该算法估计2个不同目标源的结果。由图可见，M=9，L=200，2个不同目标的仰角和方位角分别为(5°,30°)和(15°,10°)。

图2 多目标源测向散布图Fig.2 Multi-target signal sources estimation

3.1.2 具有某一相同维度角目标的多目标源测向

图3是该算法估计出相同仰角(或方位角)的目标源，其中M=9，L=200。因为该算法是估计出(θk,φk)的综合信息uk和vk，所以即使θk或φk相同，本文算法依然能有效工作。

图3 同仰角或方位角的目标源测向散布图Fig.3 Estimation of signal sources at the same elevation or azimuth

3.2 性能仿真

为了直观地反映出所提算法在不同参量下的性能，引入角度的求根均方误差(root mean square error，RMSE)，并定义为

(9)

式中:T为仿真次数；ωkq是在第q次仿真中，第k个信源仰角(或方位角)的估计值；K是信源个数(K=2)；ωk是仰角(或方位角)的精确值。定义快拍数为L，阵元数为2M-1。

3.2.1 不同快拍数下测向性能

图4针对不同快拍数下测向进行了仿真，图中SNR表示信噪比(下同)。因为采样数据随着快拍数的增加而增加，从而得到更加精确的协方差矩阵，因此得到的测向性能越好。

3.2.2 不同阵元数下测向性能

图5仿真出了不同阵元数下的测向性能。由图可见：算法的性能随阵元数的增加而提高。其原因是阵元数的增加会使分集增益增加。

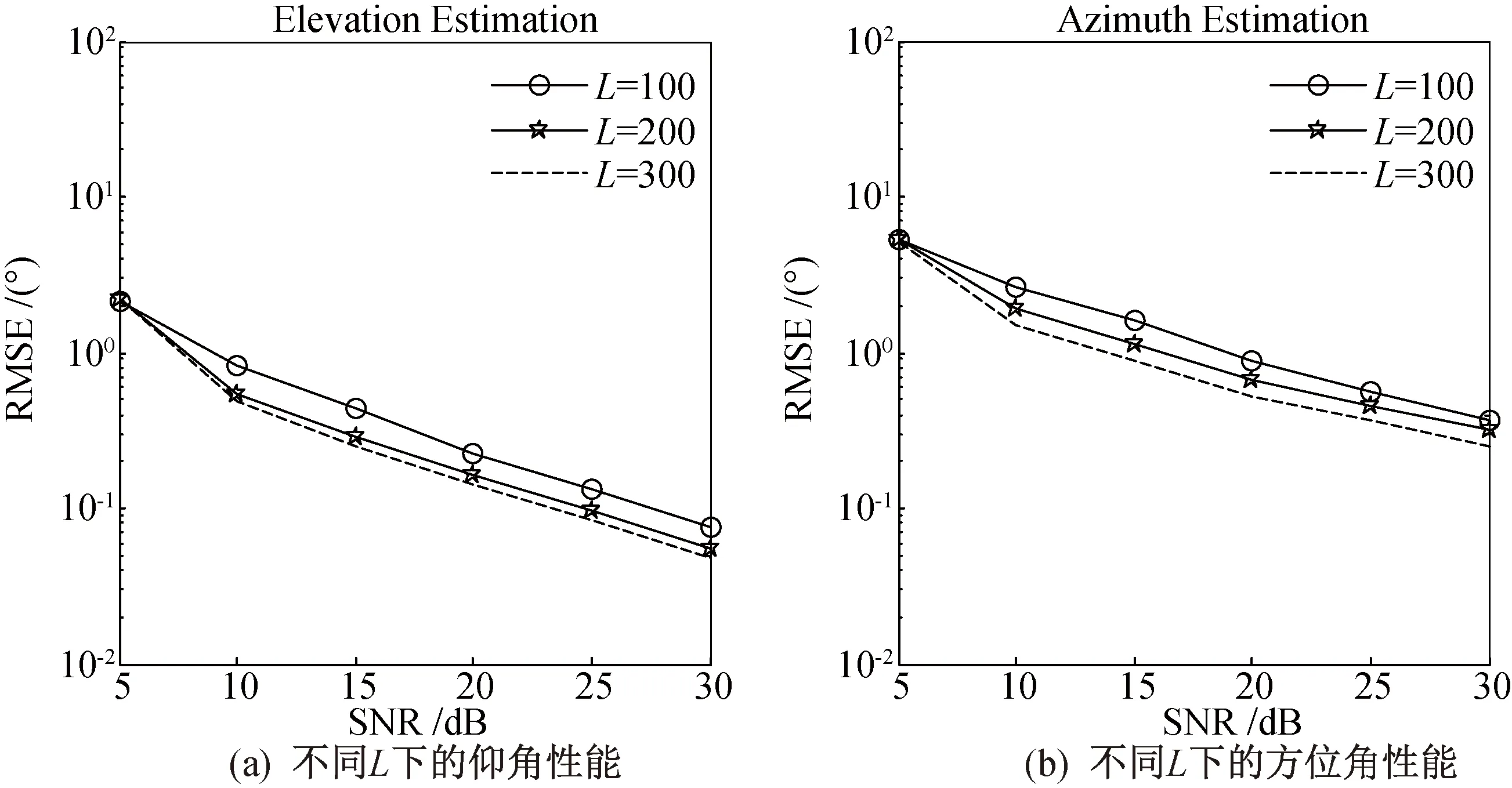
图4 不同L下的测向性能(M=9)Fig.4 Angle estimation performance with different L(M=9)

3.2.3 不同算法的计算复杂度

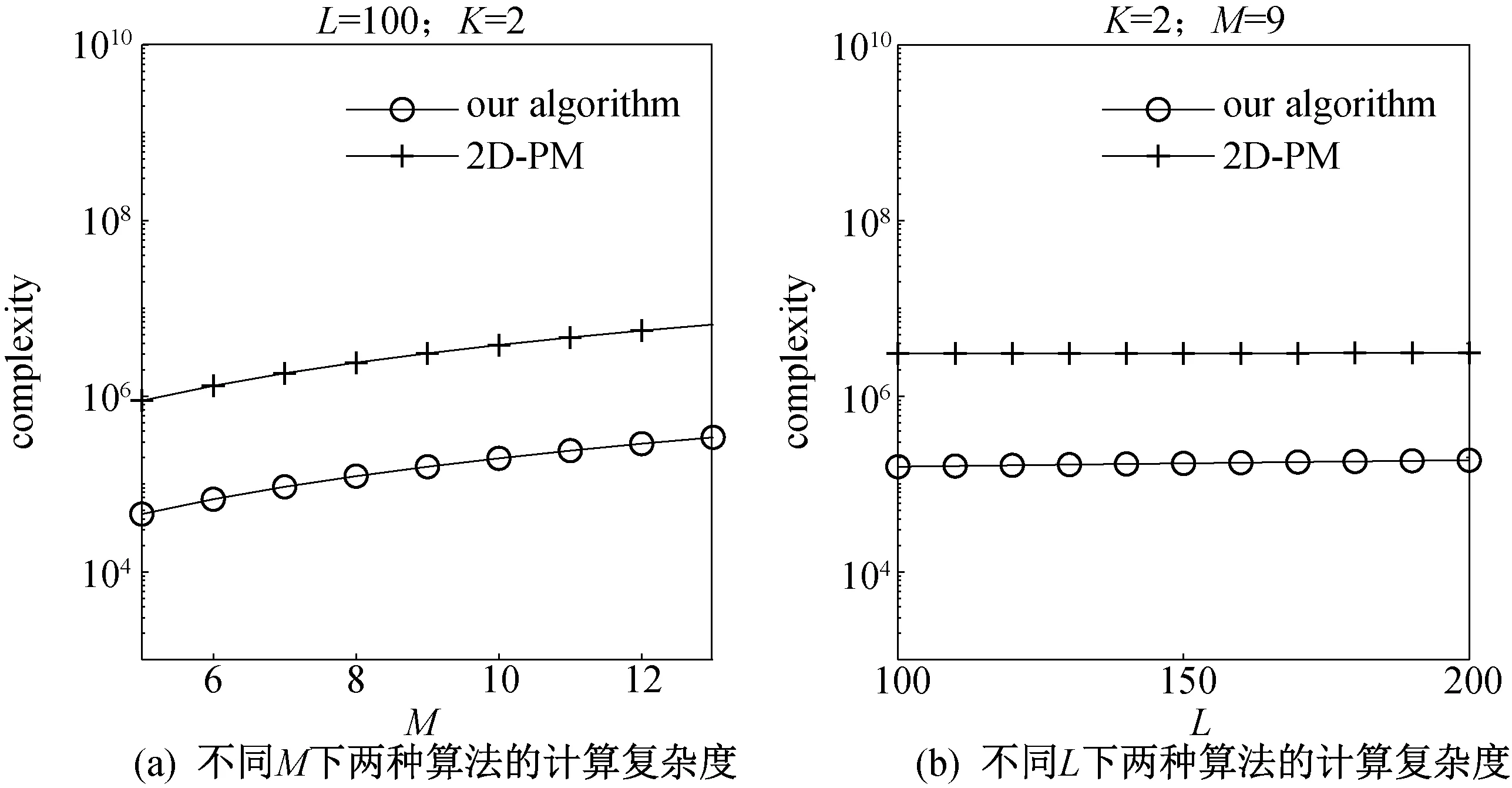
图6 不同算法的计算复杂度Fig.6 Computational complexity of different algorithms

图6仿真出了不同算法的计算复杂度。由图可见，本文算法的计算复杂度大大低于二维PM算法的计算复杂度。

3.2.4 不同算法的测向性能

图7对比了不同算法的测向性能。由图可见，本文算法的测向性能接近于二维PM算法的测向性能。

图7 不同算法的测向性能Fig.7 Angle estimation performance of different algorithms

4 结束语

本文基于十字型阵列模型提出了一种新型正交PM的空间谱测向算法。该算法引入了噪声子空间的投影算子构造伪谱，并采用一维谱峰搜索来实现二维测向。与利用二维谱峰搜索测向的二维PM算法相比，该算法大大减少了计算量，降低了计算复杂度；与利用传播算子的旋转不变特性测向的传统PM算法相比，该算法对阵列排布的要求更低。同时，该算法可实现多目标信号的测向，解决了二维角度的配对问题，也可有效估计出相同方位角(或仰角)的目标。由于该算法计算量较小，十字阵在实际应用中所占空间少，因此可广泛应用在雷达、导引头等工程测向技术中。

随着电子侦察、电子对抗的飞速发展，雷达和导引头的测向要求越来越高。本文所提算法就多目标精准测向的能力完全依赖于庞大的阵列数，且该算法尚不具备相干信号源的测向功能。因此，后续可以就如何在复杂电磁环境下实现更加轻量化、快速化、精准化测向开展持续研究。