触觉信息表征技术与分类感知试验

侯月阳，林新迪，卢 山

(1.上海航天控制技术研究所，上海 201109； 2. 上海市空间智能控制技术重点实验室，上海 201109)

0 引言

空间机器人大多配备视觉敏感器，但是在轨服务、在轨碎片清除等领域中常规的视觉感知技术受到很多限制，例如光照、遮挡等[1]。对于被操控目标的很多内在属性，例如“软”、“硬”等，难以通过视觉敏感器感知获取。对空间机器人而言，触觉也是获取环境信息的一种重要感知方式。与视觉不同，触觉传感器可直接测量多种性质特征。同时，触觉也是人类感知外部环境的一种基本模态。因此，为机器人引入触觉感知模块，不仅在一定程度上模拟了人类的感知与认知机制，又符合实际操作应用的强烈需求[2]。然而，目前航天领域所用触觉传感相关研究较少，美国国家航空航天局(NASA)开发了机械手Robonaut上使用的触觉传感器[3]，美国海军空间技术中心报道了空间机器人上触觉感知算法[4]。空间操作中的另一个重要方向是触觉交互。日本开发了面向ETS-VII卫星遥操作触觉接口[5]。加州理工学院研制了可以综合集成视觉与触觉反馈的虚拟显示系统，可辅助应用于空间探测[6]。此外，还有专家提出将触觉与视觉进行融合，从而实现异类信息的智能感知[7]。

在民用领域，科研人员对触觉分类与识别开展了广泛的研究。广义地说触觉包括接触觉、压觉、力觉、滑觉、冷热觉等与接触有关的感觉，狭义地说它是机械手与对象接触面上的力感觉[8]。一般来说，机器人触觉传感器主要有检测和识别功能。其中检测功能包括对操作对象的状态、机械手与操作对象的接触状态、操作对象的物理性质进行检测；识别功能是在检测的基础上提取操作对象的形状、大小、刚度、纹理、温度等特征，以进行分类和物体识别[9]。

经过对当前触觉物体识别工作的系统调研，将用于触觉物体识别的方法划分为三类：刚性物体、纹理材质和可变形物体[10]。这三者的典型例子为金属工件、布料和橘子。

对“刚性物体”的识别主要利用形状信息。这一方法要求机械手多次抓取同一物体以获得不同部位的信息，并利用朴素贝叶斯方法进行分类[11]。

对“纹理材质”的识别所用的物体一般具有标准的规则形状，而重点考虑其表面特性； 与视觉敏感器相比，触觉传感器可以获得更精细的纹理特性，同时，可以综合利用振动、滑擦等方式获得关于纹理材质的一些特殊性质，因此可形成对视觉敏感器的有益补充[12]。

对“可变形物体”的识别一般利用其形变特性。形变的识别同时强调物体的表面特性与内部状态，而这些内部状态无法用普通的视觉敏感器获取，形变过程需要用多变量时间序列刻画，因此给物体的识别带来很大挑战。由于物体的形变特性非常复杂，一般很难用统一的模型对其机理进行描述，因此目前广泛使用机器学习方法[13]。

机器学习成为触觉物体识别的主流方法，深度学习在触觉信号处理中的应用也开始起步，但如何有效地提取一般物体的触觉特征以实现更高效准确的分类仍然是一个难题。本文首先介绍DTW触觉序列表征，进一步研究建立DTW核实现对整个触觉序列的编码工作，然后通过触觉分类抓捕试验验证了方法的有效性。

1 基于动态序列匹配的触觉表达

机器人灵巧手指尖的触觉传感器用来捕获多层次物体特性，例如纹理特性、鲁棒性、时空特性和摩擦特性等，因此成为智能机器人领域重要的传感器模态。然而现有研究忽略了灵巧手不同指尖间采集到的物体多层次形态的联系。

文献[14]描述了自行设计开发的具有64组触觉传感模块并按照8×8规格进行排列的触觉传感器。作者分别将其安装在Schunk 2指与Schunk 3指灵巧手手指上来对一系列物体进行抓取以构建触觉数据集，并利用触觉时间序列的动态序列匹配(dynamic time warping，DTW)作为距离度量，使用了最近邻分类算法对触觉序列进行处理来进行物体识别。

使用DTW算法对时间序列进行分析建模的方法可以对时间序列进行弯曲和伸缩，对于长度不同的时间序列也具有较好的适用性，并且可以用于寻找时间序列之间的最佳匹配关系，具有较高的鲁棒性，最初广泛应用于对于声音信号的辨识中。

文献[6]将DTW算法应用于触觉序列的度量。使用DTW算法来对触觉序列进行特征提取，对于距离的衡量方法及过程如下：首先寻找一种合适的距离来作为DTW下界距离的量度。这种量度可以用于对不满足相似性要求的距离的去除，并以此来提高算法的效率和准确性。DTW的下界距离一般需要满足正确性、有效性和紧密性这三种要求。其中，正确性是指进行过滤处理后的下界距离中不可以漏掉任意一个满足条件的时间序列；有效性是指尽量减少DTW距离计算过程中所花费的时间和空间成本；紧密性则要求DTW距离与所计算的下界距离结果近似，这样可以使候选集在有限的空间中尽量包含尽量多的可用数据，并且这样也可以减少后续计算的复杂程度。

其次，通过该下界距离进行触觉序列之间变量的对应，这种匹配关系如图1所示[6]。每种匹配都使用一条虚线来表示，称其为弯曲路径，弯曲路径有多条，但是这些弯曲路径与每个样本序列之间的对应关系是唯一的。弯曲路径也必须满足以下三点：保证序列的起始点与结束点相匹配，即由起点(x1,y1)开始，而由终点(xn,ym)止；弯曲路径上的任意相邻两点(xi1,yj1)与(xi2,yj2)之间满足不等式0≤|i1-i2|≤1，0≤|j1-j2|≤1；如果(xi1,yj1)、(xi2,yj2)是弯曲路径上相连，则必须要满足i2-i1≥0,j2-j1≥0。

图1 DTW距离Fig.1 DTW distance

参照文献[11]算法进行触觉序列的建模与表征。触觉序列分类问题表述如下：给定N个训练时间序列样本S=[S1,S2,…,Si,…SN]∈Rd×Ti×N，第i个样本为Si∈Rd×Ti，其中Rd×Ti表示维度为d×Ti的实数集，d是序列的空间维度，Ti是序列的时间长度，样本对应的标签为li，i=1,2,…,N。设计一个能给新加入的样本分类的分类器。显然，怎样挖掘序列间潜在的联系来设计一个鲁棒性的分类器是个十分重要的问题。

对各个手指的触觉时间序列分类建模，手指个数为M，传感器阵列的触觉序列为o，其数值为p×q，其中p为传感器阵列的行数，q为传感器阵列的列数，随着传感器和物体接触时间的推移，采集到的p×q的触觉序列不断增加。建模过程中，将每个p×q的触觉序列按顺序排列成长度为o的列数据，因此单个手指单位时间采集到的触觉序列为一个o维的序列。

每个触觉序列的空间维度d通过M×o计算，灵巧手M个手指分别采集空间维度为o的触觉序列，然后将M个手指采集到的M组序列按顺序并排组合成d维的触觉序列。

定义两个长度为Ti和Tj的时间序列样本Si和Sj，按时间分解为

Si=[si,1,si,2,…,si,t,…,si,Ti]∈Rd×Ti

(1)

Sj=[sj,1,sj,2,…,sj,t,…,sj,Ti]∈Rd×Ti

(2)

式中：si,t∈Rd，sj,t∈Rd，均为列向量，i,j=1,2,…,Ni，j。因此得到：

(3)

式中：W为Si和Sj之间的抓取路径矩阵；wk=(i,j)k为抓取路径W的第k个元素，K为W的最后一个路径序号。所以最小匹配路径采用DTW距离描述为

(4)

虽然DTW距离匹配对于不等长的触觉时间序列能发挥最大优势，但是DTW距离不满足三角不等式和距离测度的性质，在实际应用中，式(4)在编码过程中对野值会出现奇异无解的情况，因此下一节提出一种稀疏编码方法进行解决

2 触觉序列联合稀疏编码算法

本节在DTW距离的基础上应用DTW核实现对整个触觉序列的编码工作。对于灵巧手的触觉序列分类，灵巧手一般包含几个触觉手指，每个手指可以采集到不同的触觉序列。提出基于触觉的联合稀疏编码方法，用于一个单独时间序列的不同手指间触觉信息的简单融合。这种方法不仅简单而且能挖掘不同手指采集的触觉信息指尖的内在联系，把不同的手指当做不同的传感器，然后单独进行编码。

指尖触觉序列由M个手指获得，每一个手指的触觉序列可以由训练样本线性表示，联合稀疏编码联合M个手指的触觉信息对触觉序列进行分类。

对于第i个样本序列按不同采集手指信息可分解为S=[S1,S2，…,Sm，…，SM]T，由第m个手指得到的序列为Sm∈Ro×Ti×N，m=1,2,…,M，设第m个手指采集序列对应的字典为Φ(Dm)，得到M个手指信息的联合稀疏编码为

(5)

式中：xm为第m个手指的稀疏编码矢量，m=1,2,…,M；X=[x1x2x3]∈RN×3；L21范数为X每个列向量2范数的和。利用CVX凸优化工具求解式(5)中的稀疏系数xm；利用得到的xm，根据稀疏编码理论，测试样本Sm的残差rm,c计算为

(6)

式中：KT(Sm,Dm,c)=Φ(Sm)TΦ(Dm,c)；K(Dm,c,Dm,c)=Φ(Dm,c)TΦ(Dm,c)；Dm,c为第m个手指提取的触觉序列字典中第c类的特征；Φ(Sm)T为Φ(Sm)的转置。利用式(6)得到的残差rm,c，计算M个手指的残差和rc，有

(7)

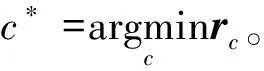
联合稀疏编码方法解决下述优化问题，即将不同手指的训练样本触觉序列求取最小二乘结果，此时所得到的不同指尖触觉序列度量为最优，有

(8)

式中：P∈R2×K为映射矩阵；K为对齐两个信号所需的步数；Si,P1,k和Sj,P2,k为不同手指的训练样本触觉序列。把k行的P表示为Pk，然后可以描述该变量矩阵P的约束：

1)P1,k∈{1,2，…,Ti},P2,k∈{1,2，…,Tj}；

2)边界条件：p1=[1,1]T,pK=[Ti,Tj]T；

3)连续性：0≤pk+1-pk≤1,k=1,2,…,K-1；

4)单调性：pk1-pk2≤0,k1≤k2。

K值是受到限制的，有

max(Ti,Tj)≤K≤Ti+Tj-1

优化问题可以等价为

(9)

式中：Z∈{0,1}K×Ti,Y∈{0,1}K×Tj为需要测量对齐的触觉序列Si,Sj的二进制选择矩阵。

3 触觉分类感知试验

3.1 数据采集

图3 抓取目标Fig.3 Grasping objects

实验中，采集触觉信息的多指灵巧手参数为手指数M=3，单手指传感器单元数o=24，单手指传感器行数p=8，但手指传感器列数q=3。多指灵巧手手指标记成手指1、手指2、手指3。手指1和手指2同步旋转并且对于关节底座对称的展开。前后掌的“展开”运动允许爪子重新配置适应不同大小、形状和方位的目标。除了扩展运动，灵巧手的3个手指设有两个关节并且由一个无刷伺服电机驱动。使用3个手指可以使灵巧安全地“把握”各种物体。

在每个时间段，从每个手指的24个传感器单元中收集触觉数据。通过重塑8×3矩阵作为一个24维向量并且假设序列长度为T，分别获得手指1、2、3的24维动态触觉序列S1∈R24×T，S2∈R24×T，S3∈R24×T。最终串联3个24维序列合并为一个单一的序列，有

(10)

选择并采集7种典型精细操作目标(包括两种柔性太阳能板、两种插头(分别为塑料和金属材质)、三种线缆(分别为柔性线缆、多股线缆、金属线缆)，用触觉信息表征目标信息，实物如图2所示。

图2 目标Fig.2 Objects

上述工作大多是利用指头上的触觉传感器，在抓取过程中一般采取精细抓取模式。另一方面，很多机械手的掌部也带有触觉传感器，这启发了一些学者利用强力抓取模式来获取触觉数据。本文也利用这种操作模式针对典型目标开展触觉序列的分类工作。在触觉数据采集过程中，每个目标被三指灵巧手抓取10次，机械臂抓取位置图如图3所示。

触觉信息反馈被接触目标的材料、形状、状态等信息影响[15]。这些触觉序列的不同可以用来进行目标分类识别，如图4所示。

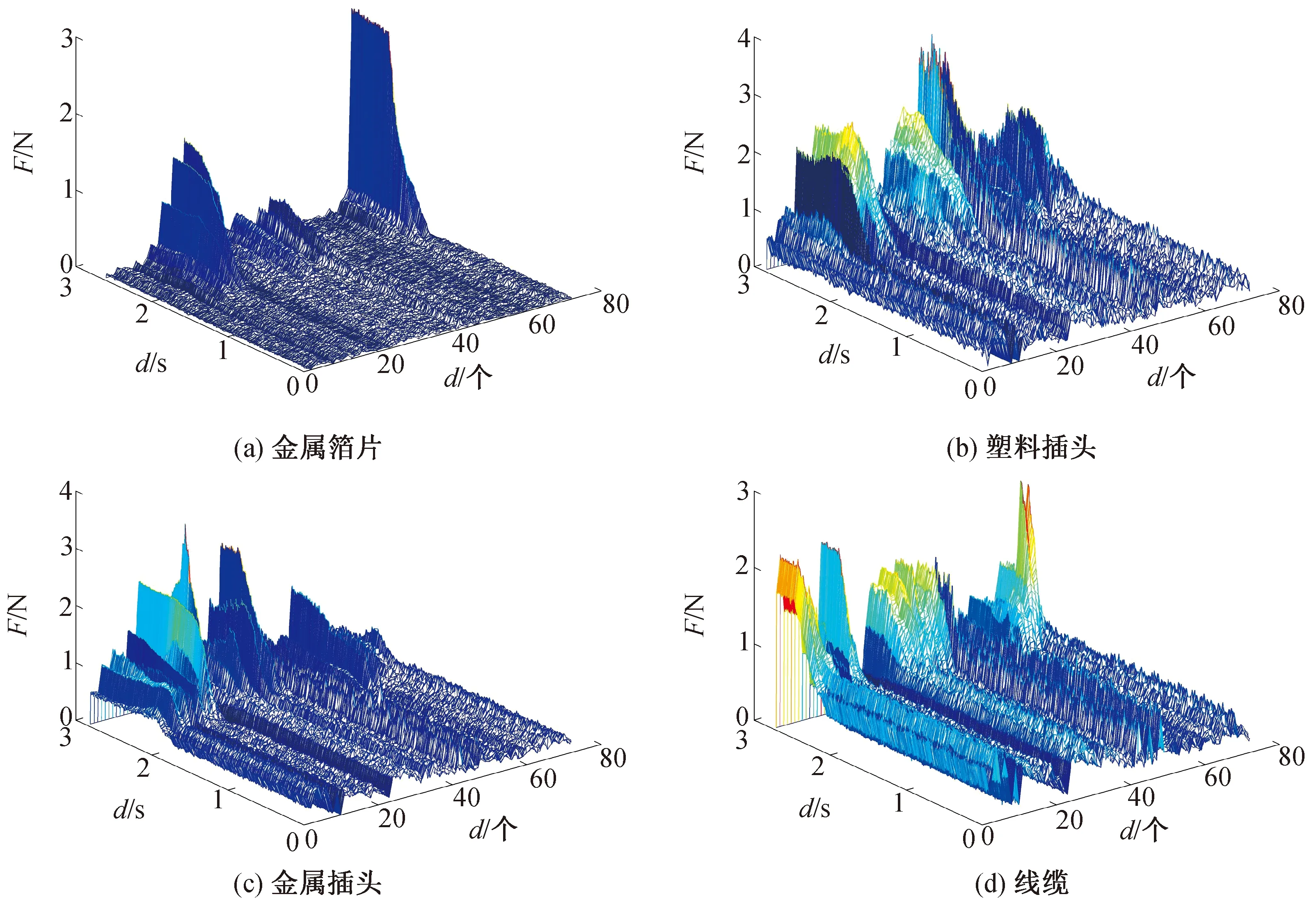
图4 触觉信息Fig.4 Tactile information

3.2 不同触觉识别方法的结果与分析

实验过程中随机10次选取9组触觉样本作为训练集样本，剩余1组作为测试集样本，每种分类方法实验准确率取10次随机分类准确率的平均值。在表1和表2为以触觉信息为特征的分类结果的混淆矩阵，其中表1是采用贝叶斯分类方法[3]的结果，表2是采用稀疏矩阵方法的分类结果。

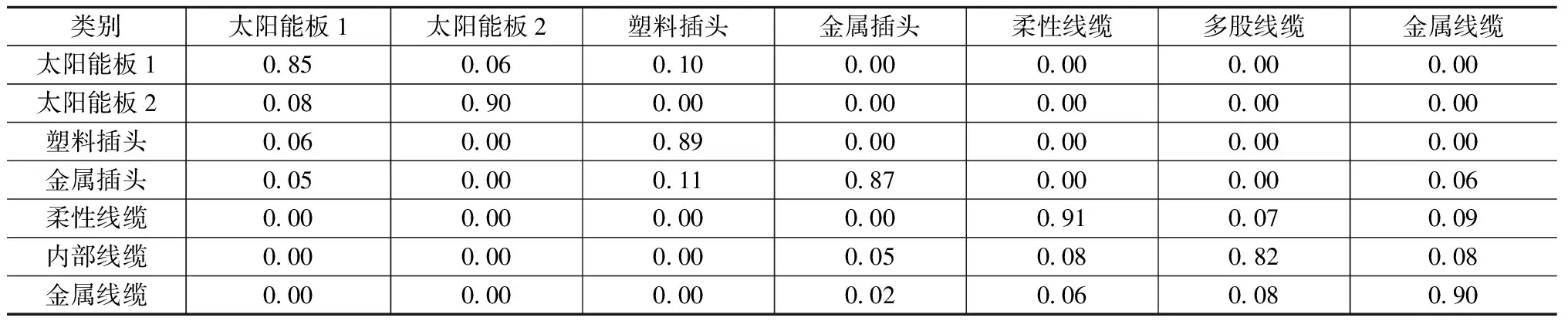
表1 采用贝叶斯方法的触觉混淆矩阵

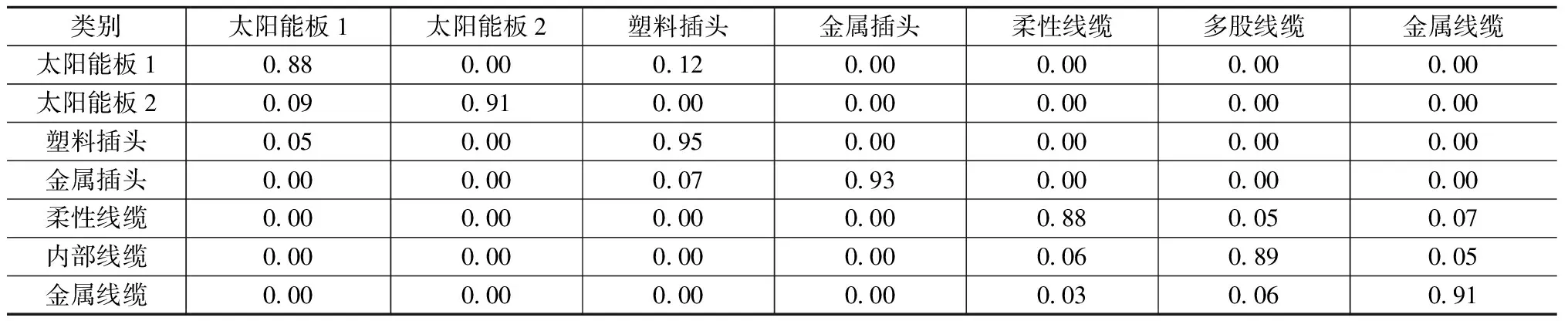
表2 采用稀疏编码的触觉混淆矩阵

从上面两个混淆矩阵中可以看出，由于抓取姿态的不同，不同类目标之间的区分度较好。但对同一类目标(如不同的线缆)，存在一定的混淆。此外，采用贝叶斯分类方法的总体识别率为87.71%，采用稀疏编码方法的总体识别率为90.07%，结果表明稀疏编码方法对于触觉分类准确率有2.36%的提升。

4 结束语

本文研究了采用触觉进行目标分类感知的问题，重点研究了基于联合稀疏编码的触觉信息表征方法，采用贝叶斯分类方法作为对比，进行了典型目标分类试验，试验结果表明总体识别率达到了90.07%，相比与贝叶斯分类方法，分类准确率提高了2.36%。由试验可知，不同类目标之间的区分度较好，而对于同类目标(如不同线缆)则混淆较大，说明单一依靠触觉手段难以完全区分目标，因此后续将研究引入其他信息源辅助进行分类感知的问题。