调频连续波合成孔径雷达滑动聚束成像算法
2019-10-26陈翔,王辉
陈 翔,王 辉
(上海卫星工程研究所,上海 201109)
0 引言
传统合成孔径雷达(SAR)多采用脉冲体制,相同条件下调频连续波(FMCW)技术所需的峰值发射功率较低,固态放大器即可满足需求,故具有成本低的特点。然而,相较于脉冲体制,FMCW扫频周期较长,电磁波发射与接收时间不一致引入额外的距离—方位耦合[1],快时间走动项的引入导致传统的走停模型不再成立,因此FMCW SAR处理不同于传统脉冲SAR。2010年中国科学院电子学研究所王宇[2]提出了一种考虑快时间走动项的FMCW SAR条带成像模式的处理算法,但由于滑动聚束模式总的多普勒历程较大,存在不同程度的方位混叠,因此该算法在滑动聚束模式下不适用。目前滑动聚束模式成像数据的处理方法有子孔径法和两步式成像法两种[3-4]。子孔径法各子块数据之间需要一定比例的重叠,且后期图像拼接较为复杂,成像效率较低,难以满足一次成像的需求[5],两步式算法可以对方位向点统一处理,要求方位向扩展的点数较少。然而由于脉冲频率的限制,会产生图像域混叠。
针对子孔径算法和传统两步式成像算法的局限性,该文提出了一种改进的两步式FMCW SAR成像算法。首先,构建FMCW滑动聚束模式的回波信号模型,推导点目标回波的数学公式,准确表示扫频周期内瞬时斜距的变化对回波信号的影响;继而,基于点目标回波的距离多普勒域、解方位频谱混叠、距离徙动校正(RCMC),并在方位频域去斜实现两维聚焦;最后,通过仿真验证实验对比分析传统两步式算法与该文所提算法,并给出相应结论。
1 FMCW 滑动聚束回波信号模型
滑动聚束成像模型如图1所示。图中,R0为点目标到平台航线的最短距离,搭载FMCW SAR的平台以速度v沿着x轴正方向飞行,天线波束中心以恒定的角速度w从斜视角为+θ转动到斜视角为-θ,天线各个时刻的波束中心线延长相交于地面以下斜距为Rrot的点O。

图1 滑动聚束成像模型Fig.1 Sliding spotlight imaging model
为了描述滑动聚束模式对方位向分辨率的提高程度,定义滑动因子
(1)
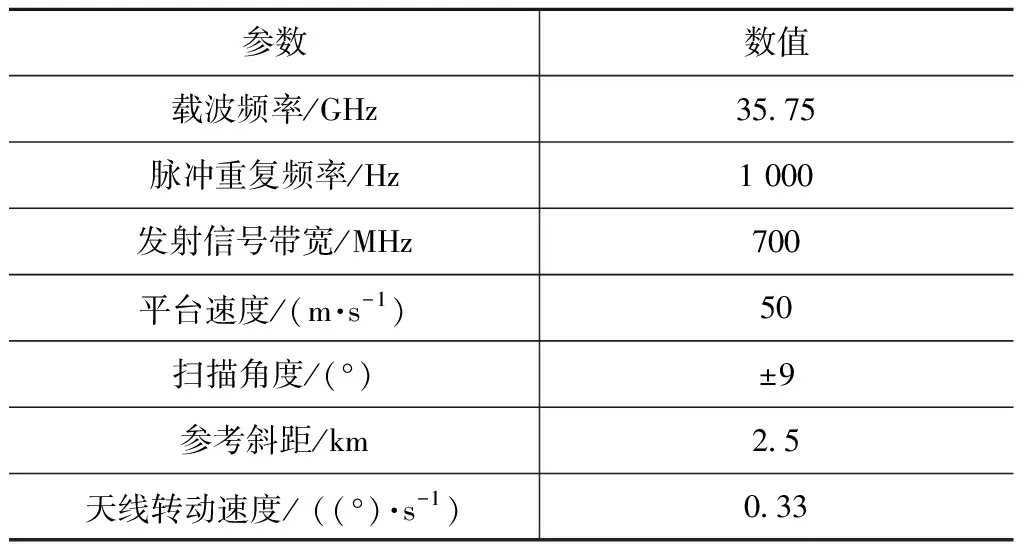
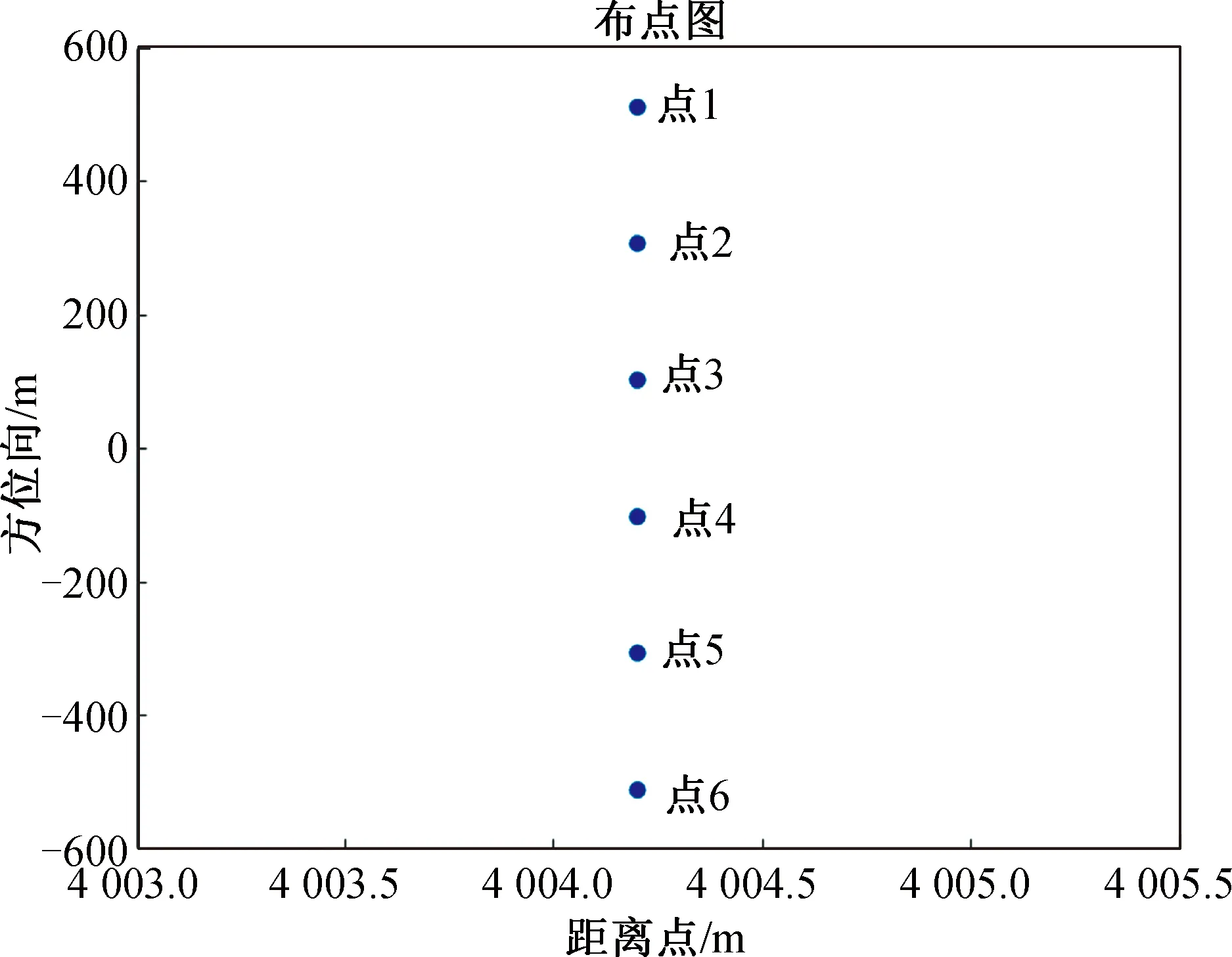
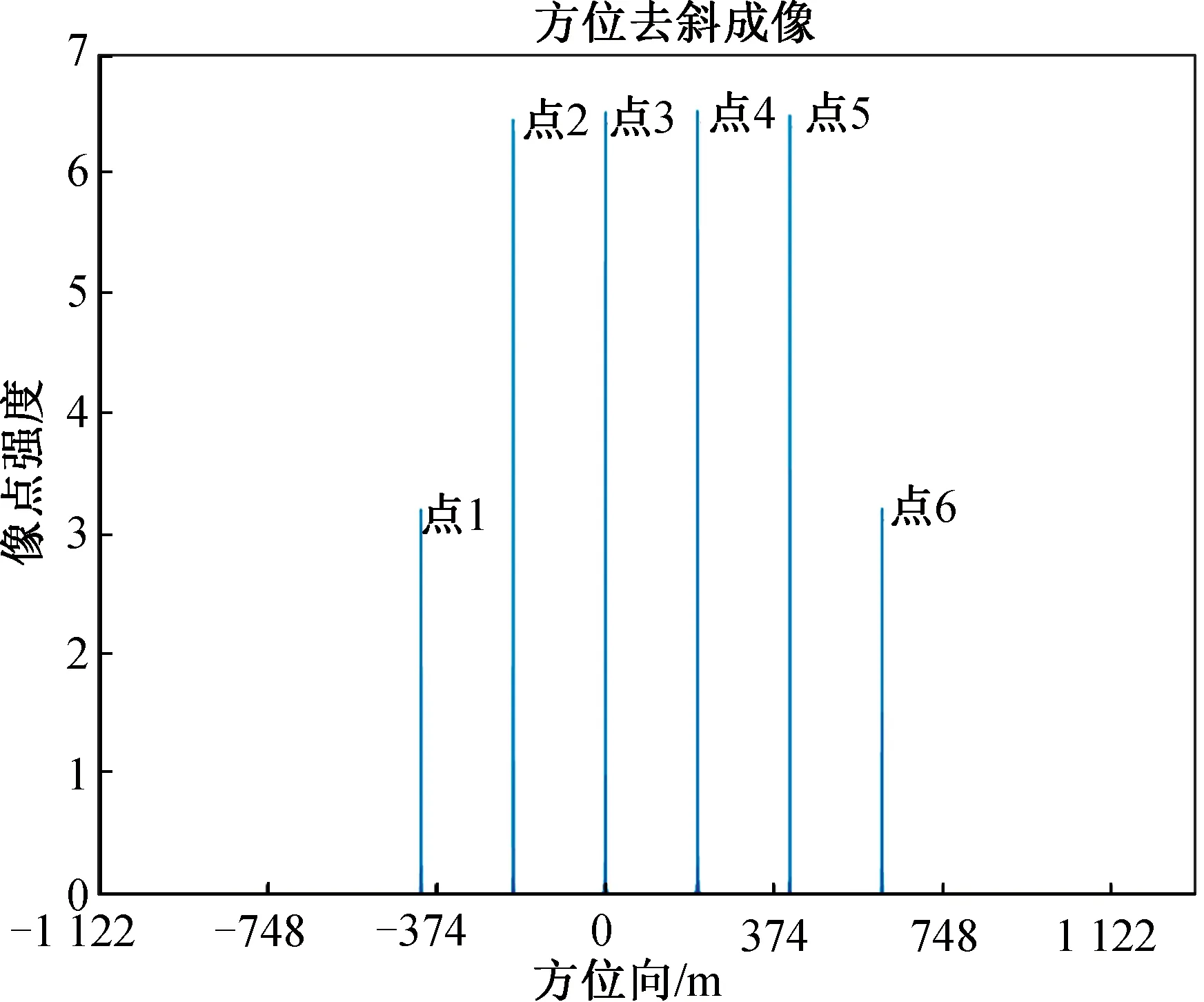
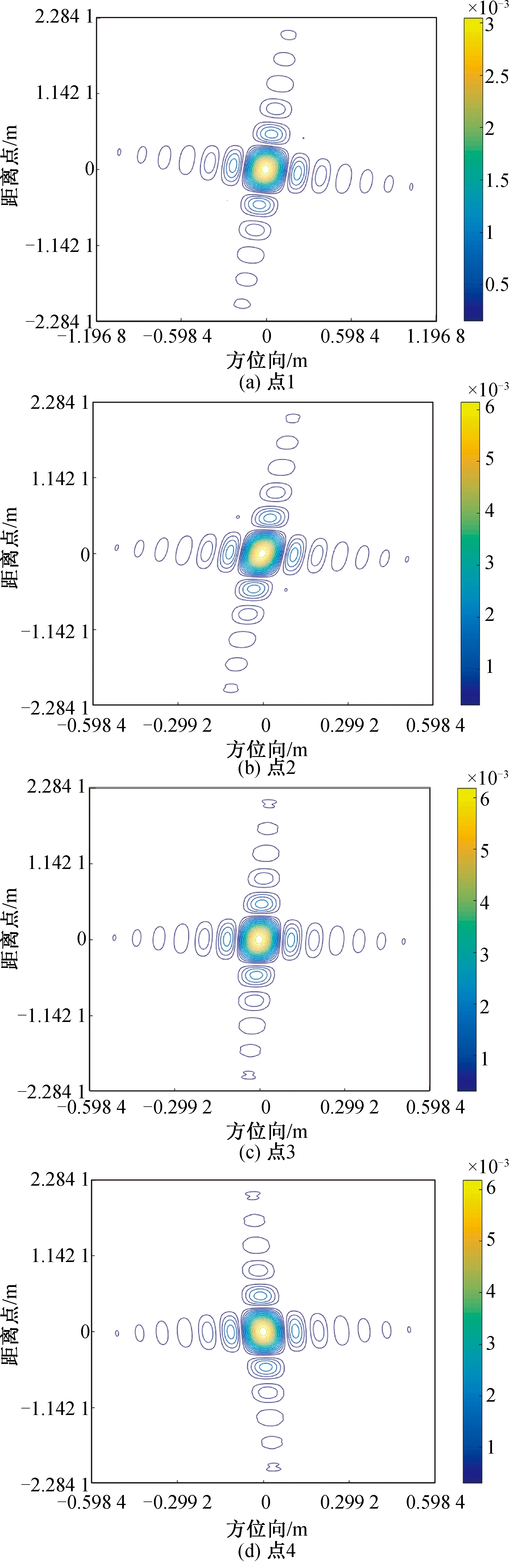
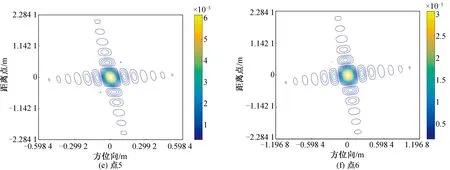
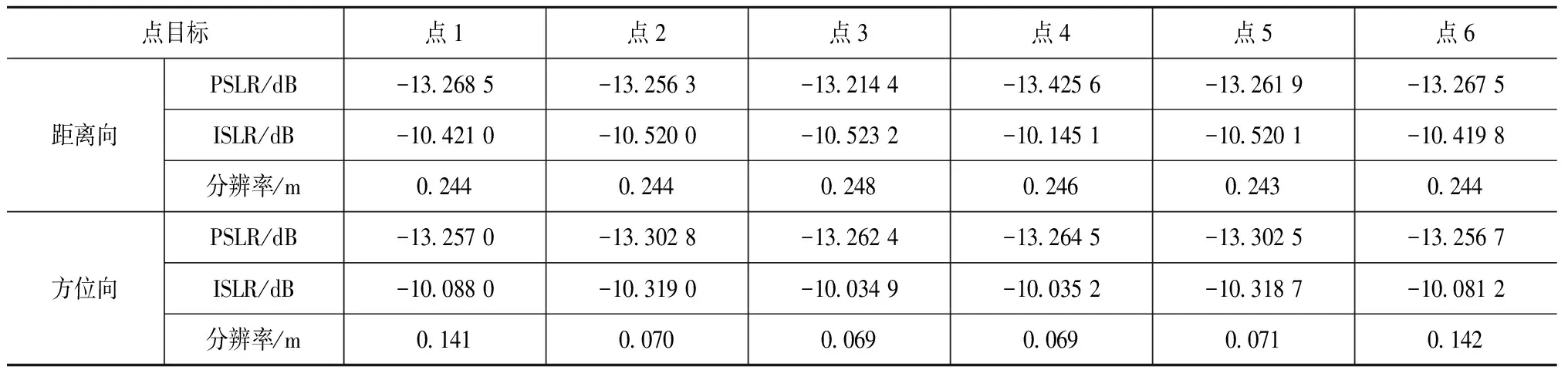
式中:0 非“走—停”回波模型如图2所示,对于一个点目标,设t时刻发射的FMCW信号发射时,斜距为R(t),斜视角为θc。经过td后被接收到,接收时刻的瞬时斜距为R(t+td),斜视角为θd,存在 (2) (3) (4) 式中:t为总时间变量;t0为零多普勒时间。 图2 回波模型Fig.2 Echo model 将式(3)、式(4)代入式(2),可以解得 (5) 式中:α=(1-v2/c2)-1。 发射的FMCW信号为 式中:f0为载波频率;tr为距离向时间变量;Kr为发射信号的调频率。最短斜距为R0的回波接收信号为 sr(tr,ta,R0)=σ(t0,R0)wa(ta)s0(tr-td) (6) 式中:σ(t0,R0)为零多普勒时间为t0、最短斜距为R0的点目标P(X0,R0)的后向散射系数;ta为方位向时间变量;wa(ta)为滑动聚束模式的方位向窗函数。 FMCW SAR回波信号一般都是采用dechirp(去斜)接收的方式,选定一个参考斜距Rc,则本振时延为tc=2αRc/c,参考信号为 (7) 去斜接收的回波信号为 sd(tr,ta,R0,tc)=sr(tr,ta,R0)·sref(tr,ta,tc)= σ(t0,R0)wa(ta)·exp[-j2πf0(td-tc)]· exp[-j2πKr(td-tc)(tr-tc)]· exp[jπKr(td-tc)2] (8) 式中:exp[-j2πf0(td-tc)]表征点目标的方位向位置;exp[-j2πKr(td-tc)(tr-tc)]表征点目标的距离向位置;exp[jπKr(td-tc)2]为残余视频项(RVP),可以在距离频域去除RVP项[6-7]。 sr(tr,ta,R0,tc)= σ(t0,R0)wa(ta)·exp[-j2πf0(td-tc)]· exp[-j2πKr(td-tc)(tr-tc)] (9) 式中:IFFTr为距离向快速傅里叶变换;FFTr为距离向快速傅里叶变换;fr为距离向频率变量。Kr乘以距离向时间就是fr,因此有 sr(fr,ta,R0,tc)=σ(t0,R0)· exp[-j2π(f0+fr)(td-tc)] (10) 将td代入式(10)可得去斜接收方式接收的回波信号,即 sn(fr,ta,tc)=σ(X0,R0)wa(ta)· (11) 为了得到点目标的方位频域,对式(11)进行方位向FFT。忽略FFT对方位向窗函数的影响,即Wa(fa)与wa(ta)形状近似一致。 Sn(fr,fa,tc)=FFTa(sn(fr,fa,tc))= (12) (13) 将ta代入Φ(fr,fa),可得 Φ(fr,fa)= (14) 分析快时间走动项对成像的影响,td时间内平台运动的距离 (15) 表1为一组机载参数和一组星载参数。在正侧视情况下,机载参数下dX为1.3×10-5m,星载参数下dX为0.24 m,这个包络误差相对于现有距离分辨率的机载、星载SAR均是可以忽略的。考虑相位,以Ka波段为例,机载参数的相位误差0.001 6 rad,星载参数的相位误差28.6 rad,星载参数在Ka波段下再使用传统“走—停”模型方位向将完全无法聚焦。 表1 机载与星载参数 而对于方位向聚焦所需要计算的多普勒中心频率fdc和方位向调频率Ka来说,机载、星载情况下快时间走动项的影响均在10-9(dX/Rc)量级,完全可以忽略,因此,在FMCW SAR滑聚成像模式中fdc、Ka两个参数不受来自快时间走动项的影响。 基于两步法的FMCW SAR滑动聚束模式成像的流程如图3所示。去除RVP项后运用两步法。两步法的第一步为基于去斜操作的方位预滤波处理,能够有效解决滑动聚束模式的多普勒频率混叠;第二步为对解除方位混叠的信号RCMC,聚焦成像。FMCW SAR采用去斜接收方式,其信号回波域可以看作“伪距离频域”,对回波信号做方位向FFT操作后即可得到二维频域信号[8]。继而通过RFM滤波器在二维频域进行校正,该滤波器能够补偿参考距离处的相位,参考距离处的数据能够完全的聚焦。一致压缩完成之后的残余相位采用Stolt插值的方法去除。插值后的方位时域是混叠的,若是在时域进行方位匹配滤波,需要对时域也进行一次解混叠操作,因此本文采用方位去斜方法在方位频域成像以减少运算量。 图3 算法流程图Fig.3 Algorithm flowchart 方位向总的多普勒带宽为 Ba=KrotTa+Bdop (16) (17) s1(fr,ta)=sn(fr,ta,tc)·H1 (18) 对回波信号乘以H1,将天线波束中心转动引入的多普勒历程消除掉,因此之后的FFT将不会出现混叠。需要注意的是,若是该滑动聚束成像模式下的Bdop自身已经大于PRF,则会出现即使将天线波束转动引入的多普勒历程去除依旧出现方位频谱混叠现象。 (19) s2(f′a,t′a)=FFTa(s1(fa,ta))H2 (20) 式中:t′a为重采样后的时间变量。并且为了保证插值重采样的有效性,新的采样频率Fnew相较于Ba需满足奈奎斯特采样定律,过采样率一般选用1.2~1.5。对s1进行补零操作后再进行方位向FFT并乘以H2,这一步并不是时频域转换,而是为了完成sinc插值。重采样后的总的方位向点数为 (21) 重采样完成后需要将方位去斜中去除掉的频率分量用H3补偿回来。 (22) S3(fr,f′a)=FFTa(s2(fr,t′a))H3= σ(X0,R0)Wa(f′a)exp[-jΦ(fr,fa)] (23) S3和Sn在形式上是一致的,但方位采样率由PRF转变为Fnew,方位向频率变量也从fa变为f′a。S3可以理解为回波信号做了一步没有方位向混叠的FFT操作,此时得到了回波信号的距离多普勒域,由于Kr(tr-tc)即为fr,可以将去斜接收的回波看作是处于距离频域方位时域,因此在方位向FFT之后,得到了点目标的二维频域。 参考距离处的RFM滤波器为 ΦR(fr,f′a)= (24) 该滤波器能够补偿参考距离处的相位,参考距离处的数据能够完全聚焦。经过RFM滤波后,二维频域中的残余相位剩下 (25) 残余相位包括(R0-Rc)与t0两项,分别对应着点目标的距离向和方位向位置。 本文通过Stolt插值来校正残余RCMC,残余距离方位耦合,其表达式为 Stolt插值将fr映射到新的非线性的距离频率轴f′r,距离频域中仅剩下线性项,不再携有高阶项。 S5(f′r,f′a)= σ(X0,R0)Wa(f′a)exp[jΦStolt(f′r,f′a)] (26) ΦStolt(f′r,f′a)= (27) 对S5进行距离IFFT,得到 S6(t′r,f′a)=σ(X0,R0)Wa(f′a) (28) 此时的方位时域依旧是存在混叠的[9],可以参照在回波域解方位频谱混叠的方式解时域混叠,但运算较大,考虑到此时的方位频域已不存在混叠,采用方位频域去斜聚焦[10-11]。利用H4给方位频域添加大小为Ka2的方位向调频率,再经过方位向IFFT得到S7。 (29) (30) S7(t′r,t′a)=IFFTa(S6·H4)= (31) 式中:压缩脉冲包络pr为距离向窗函数的傅里叶逆变换。对于矩形窗,pr为sinc函数。 利用H5将S7里的二次项抵消掉,相当于将频域中的线性项去除,再进行一次方位向IFFT,即可在方位频域得到良好聚焦的SAR图像S8。 (32) S8(t′r,f′a)=IFFTa(S7·H5)= (33) 式中:压缩脉冲包络pa为方位向窗函数的傅里叶逆变换。 S8已是良好聚焦的图像。若是想获得高保相的图像,可以将最后一个相位项补偿掉。S9即为最终所得的聚焦像点。 (34) S9(t′r,f′a)= (35) 为验证本文所述算法的正确性,根据表2的系统参数进行了仿真实验。 表2 仿真参数 在成像场景中布置了如图4所示的等间距的6个点目标,点1和点6位于场景边缘,属于非全孔径成像点。图5给出了Stolt插值后直接二维IFFT后的剖面图,图6给出了方位去斜成像的剖面图,图中的每个峰对应一个像点。图7为6个点目标成像结果32倍插值后的轮廓图。表3给出了6个点目标的距离向、方位向的峰值旁瓣比、积分旁瓣比以及分辨率。 图4 所布点阵图Fig.4 Point map 图5 未方位去斜成像图Fig.5 Unoblique imaging 图6 方位去斜成像图Fig.6 Oblique imaging 图7 32倍插值仿真结果Fig.7 Simulation results with 32 times interpolation 续图7 32倍插值仿真结果Fig.7 Simulation results with 32 times interpolation 点目标点1点2点3点4点5点6距离向PSLR/dB-13.268 5-13.256 3-13.214 4-13.425 6-13.261 9-13.267 5ISLR/dB-10.421 0-10.520 0-10.523 2-10.145 1-10.520 1-10.419 8分辨率/m0.2440.2440.2480.2460.2430.244方位向PSLR/dB-13.257 0-13.302 8-13.262 4-13.264 5-13.302 5-13.256 7ISLR/dB-10.088 0-10.319 0-10.034 9-10.035 2-10.318 7-10.081 2分辨率/m0.1410.0700.0690.0690.0710.142 从图5和表3可以看出,边缘点因是非全孔径成像,像点强度和32倍插值后的3 dB宽度均只有全孔径成像点的1/2。从像点所处的位置可以看出,插值完成后直接两维IFFT在方位时域是存在混叠的,解图像域方位混叠是必要的。图6可以看出,像点所处的位置与布点图中点所处位置一致,不再出现混叠,可以证明方位去斜成像操作是有效的。 图7和表3可以看出,通过该文所提算法从边缘点到全孔径成像点均良好聚焦,其距离向、方位向峰值旁瓣比、积分旁瓣比均与理论值吻合。相同参数下的FMCW SAR条带模式的方位向32倍插值后的3 dB宽度为264。滑动聚束模式的3 dB宽度条带模式的比值约为0.449 1,与仿真所用参数计算出的方位向分辨率改善因子A=119/264=0.450 8一致。 该文针对FMCW SAR滑动聚束模式成像进行研究,首先建立考虑快时间走动项的FMCW回波模型,进而针对传统两步式成像处理算法会出现图像域混叠的问题,提出了改进的两步式成像处理算法。通过研究,得出如下结论: 1) 传统两步式成像算法能够解决方位向频谱混叠问题,但在PRF较低的情况下会出现图像域混叠。若要克服这种频谱混叠,需要大幅提高PRF,这会导致雷达接收回波数据的增加,给处理带来压力。 2) 改进的两步式成像算法在传统两步式成像算法解除了方位向频谱混叠的基础上,在方位频域去斜操作完成聚焦,不受PRF的限制,不会产生图像域混叠。 该算法的不足之处在于采用全孔径成像降低了运算量,但数据处理过程中内存占用量大。Stolt插值是理论上精度最高的方法,但其是串行计算,运算速度慢,后续可以尝试在不降低成像精度的前提下换用速度更快的徙动校正方法。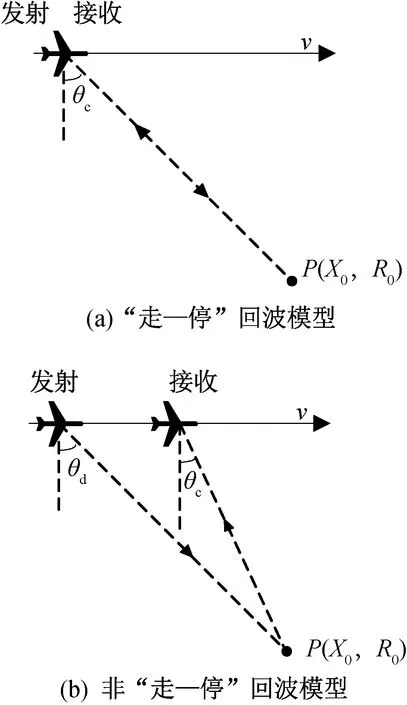

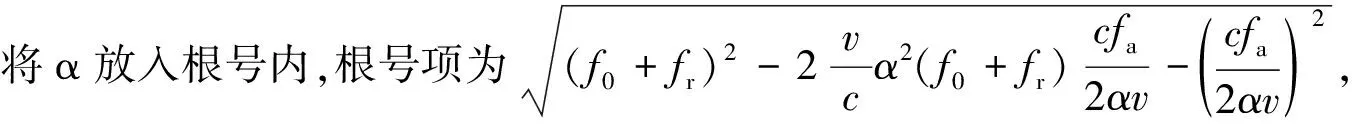

2 滑动聚束ωk成像算法

2.1 解方位混叠
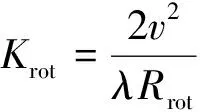
2.2 一致压缩
2.3 Stolt插值
2.4 方位频域去斜成像
3 仿真结果

4 结论
